COVID-19/Mathematische Modellierung/DiMoT

Krankheitsmodellierungzeitspanne (Disease Modelling Time span = DiMoT), über den die Krankheitsentwicklung mathematisch beschrieben wird.

Einführungsbeispiel[Bearbeiten]

Als einführendes Beispiel nehmen wir an, dass der Krankheitsmodellierungszeitraum 14 Tage sei. In diesem Krankheitsmodellierungszeitraum sollte eine Funktion erstellt werden, die die Infektiösität über diesen Zeitraum von 14 Tage darzustellen. Die Funktion sollte 100 sein, wenn 100% der infizierten Patienten an diesem Zeitpunkt selbst infektiös sind.

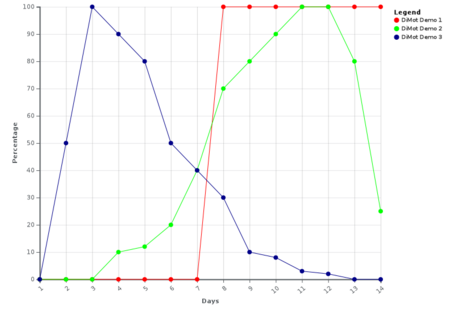
Die Anteile der Infizierten kann unterschiedliche Verläufe darstellen. Die Kurvenverläufe sind fiktiv und sollen lediglich das Prinzip der Krankheitsmodellierungszeitspannen veranschaulichen.

mit der roten Kurve wird ein Verlauf dargestellt, bei die ersten 7 Tage kein Infektiösität vorliegt und danach 100% der Infizierten infektiös.
in der blauen Kurve sind nach 3 Tagen 100% infektiös, danach werden immer weniger infizierte Personen infektiös.
in der grünen Kurve steigt der Anteil der infizierten Personen bis zum 11. Tag auf 100% an und dann bleibt dieser Anteil für einen weiteren Tag auf 100%. Danach sinkt der Anteil der infektiösen Personen wieder ab.

Definition: DiMoT[Bearbeiten]

Eine Krankheitsmodellierungzeitspanne (Disease Modelling Time span - DiMoT) kann wie folgt definiert werden:

stetiger Fall: DiMoT als ein Intervall $T:=[a,b]\subset \mathbb {R}$
diskreter Fall: DiMoT als eine endliche Teilmenge der reellen Zahlen $T\subset \mathbb {R}$ with $|T|=n\in \mathbb {N}$ .

Beispiel[Bearbeiten]

Für eine Krankheitsmodellierungzeitspanne (Disease Modelling Time span - DiMoT) werden im Folgenden für den diskreten und stetigen Fall jeweils ein Beispiel genannt, das sich auf die obige Abbildung bezieht. folgt definiert werden:

stetiger Fall: DiMoT als ein Intervall $T:=[0,14]\subset \mathbb {R}$
diskreter Fall: DiMoT als eine endliche Teilmenge der reellen Zahlen $T=\{1,2,...,14\}\subset \mathbb {R}$ with $|T|=14\in \mathbb {N}$ .

Dichtefunktionen und Wahrscheinlichkeitsdichten[Bearbeiten]

Wahrscheinlichkeitsdichten oder allgemeiner Dichtefunktionen können ebenfalls auf dem Krankheitsmodellierungszeitraum definiert werden.

eine Wahrscheinlichkeitsdichte über den Krankheitsmodellierungszeitraum kann z.B. angeben, wie die Verteilung der Infektionen über die Zeitpunkte der DiMoT verteilt sind.
eine allgemeine Dichte erlaubt die Masseverteilung über die DiMoT. Im stetigen Fall kann so z.B. durch ein Integral über ein Teilintervall des Krankheitsmodellierungszeitraum die Anzahl der infizierten Personen in diesem Zeitinterval berechnet werden.
wenn der Infektionszeitpunkt zwischen dem 11., 12. oder 13. Tag vor dem Meldezeitpunkt grob bestimmt werden kann, dann ordnen wir $+{\frac {1}{3}}$ für alle drei spezifischen Tage -11,-12 und -13 zu. Damit wird insgesamt die Masse 1 verteilt und entsprechend der Unsicherheit auf die Tage 11., 12. oder 13. Tag vor dem Meldezeitpunkt verteilt.
die folgenden Kurven zeigen verschiedene Beispiele für Werte - diese Werte sind keine echten Werte. Sie sollen die Grundprinzipien für Funktionen auf der DiMoT-Menge als Domäne veranschaulichen.

Absolute Anzahl und Wahrscheinlichkeitsdichte
Day	Infected - Count	Probability Density
-13	1	0,0102040816326531
-12	18	0,183673469387755
-11	15	0,153061224489796
-10	34	0,346938775510204
-9	12	0,122448979591837
-8	7	0,0714285714285714
-7	9	0,0918367346938776
-6	2	0,0204081632653061
-5	0	0
-4	0	0
-3	0	0
-2	0	0
-1	0	0
0	0	0

Nun soll aus den absoluten Werte ein Wahrscheinlichkeitsverteilung entstehen, so muss die Verteilung im diskreten bzw. stetigen Fall normiert werden.
sind alle Werte für die absolute Häufigkeit gegegen, erhält man eine Wahrscheinlichkeitsverteilung im diskreten Fall durch die Berechnung der relativen Häufigkeiten
Für eine nicht-negative integrable Funktion über das DiMoT-Intervall $[a,b]$ wird aus der Dichtefunktion $f:[a,b]\to \mathbb {R} _{o}^{+}$ eine Wahrscheinlichkeitsdichte mit:

{\begin{array}{rcl}p:[a,b]&\to &\mathbb {R} _{o}^{+}\\x&\mapsto &\displaystyle {\frac {1}{\displaystyle \int _{a}^{b}f(t)\,dt}}\cdot f(x)\\\end{array}}

Wahrscheinlichkeitsfunktionen[Bearbeiten]

Wahrscheinlichkeitsfunktionen über die DiMoT $T$ ordnen jedem Zeitpunkt $t\in T$ eine Wahrscheinlichkeit $f(t)\in [0,1]$ . D.h. über Wahrscheinlichkeitsfunktionen wird die Wahrscheinlichkeit für das Eintreten eines bestimmten Ereignisses zum Zeitpunkt $t\in T$ angegeben. Ein Wahrscheinlichkeitsfunktion $f$ ist aber in der Regel keine Wahrscheinlichkeitsdichte, denn eine Wahrscheinlichkeitsfunktion $f$ verletzt in der Regel die Normiertheit von Wahrscheinlichkeitsmaßen, d.h.

im diskreten Fall: $T:=\{t_{0},t_{1},\ldots t_{n}\}\qquad \sum _{k=0}^{n}f(t_{k})\not =1$ bzw.
im kontinuierlichen Fall: $T:=[a,b]\qquad \int _{a}^{b}f(t)dt\not =1$

Faltung von Funktionen[Bearbeiten]

In diesem Abschnitt wird in die Faltung von Funktionen eingeführt. Die Faltung von Funktionen kann in dem Kontext von COVID-19 dazu verwendet werden, aus den Meldezeitpunkten einer Infektion die Verteilung der Infektionszeitpunkte zurückzurechnen.

Dies wird an dem folgenden fiktiven Beispiel veranschaulicht. Wir nehmen dabei an, dass die folgende Kurve die gemeldeten COVID-19-Fälle darstellt. Die positiven Fälle werden an dem Tag in die Tabellenkalkulation eingetragen, an dem die Probe als positiv gemeldet wurde. Der folgende Graph zeigen eine fiktive Abfolge von Fallzahlen.

Alle positiv getesteten Personen werden ferner befragt, bei welchem Ereignis sich die Probanden ggf. angesteckt haben könnten.

Wenn es keine Informationen zu dem Ansteckungsereignis gibt, so werden diese in folgenden Verteilung nicht aufgeführt.
Wenn man ein Ereignis identifizieren kann, dass z.B. 8 Tage vor dem Meldezeitpunkt der Infektion liegt, addiert man bei -8 die aggregierten Fallzahlen (also z.B. +1).
Wenn es zwei mögliche Infektionszeitpunkte vor 8 und vor 10 Tagen in Frage kommen, addiert man bei -8 und -10 als aggregierte Infektionszeitpunkte jeweils 0,5.

Die absoluten Häufigkeiten seien dabei wie folgt in dem Graph dargestellt.

Abschließend wird die zeitliche Verzögerung oder die rückwirkende Darstellung der Fallzahlen für Infektionszeitpunkte dargestellt. Die zweit roten Kurven zeigen die zurückgerechneten Infektionszeitpunkte für beiden unterschiedlichen Faltungsfunktionen:

Dirac-Maß auf der DiMoT beim ein einzelnen Zeitindex die gesamte Wahrscheinlichkeitsmasse trägt,
diskretes Wahrscheinlichkeitsmaß auf endlich viele Zeitindizes der DiMoT.

Siehe auch[Bearbeiten]

Kurs:Räumliche Modellbildung
Faltung von Funktionen
CSV2Chart - Diagrammerstellung aus CSV-Dateien