Erste Schritte[Bearbeiten]

Modellierung mit Tabellenkalkulation[Bearbeiten]

Die Modellierung stellt dar, wie viel Kohlenstoffmonoxid von Autos in der Stadt Landau (Pfalz) ausgestoßen wird und wie sich dieser Stoff mit der Zeit (im Stundentakt und bei Windstille) verteilt.

Einteilung der Stadtkarte[Bearbeiten]

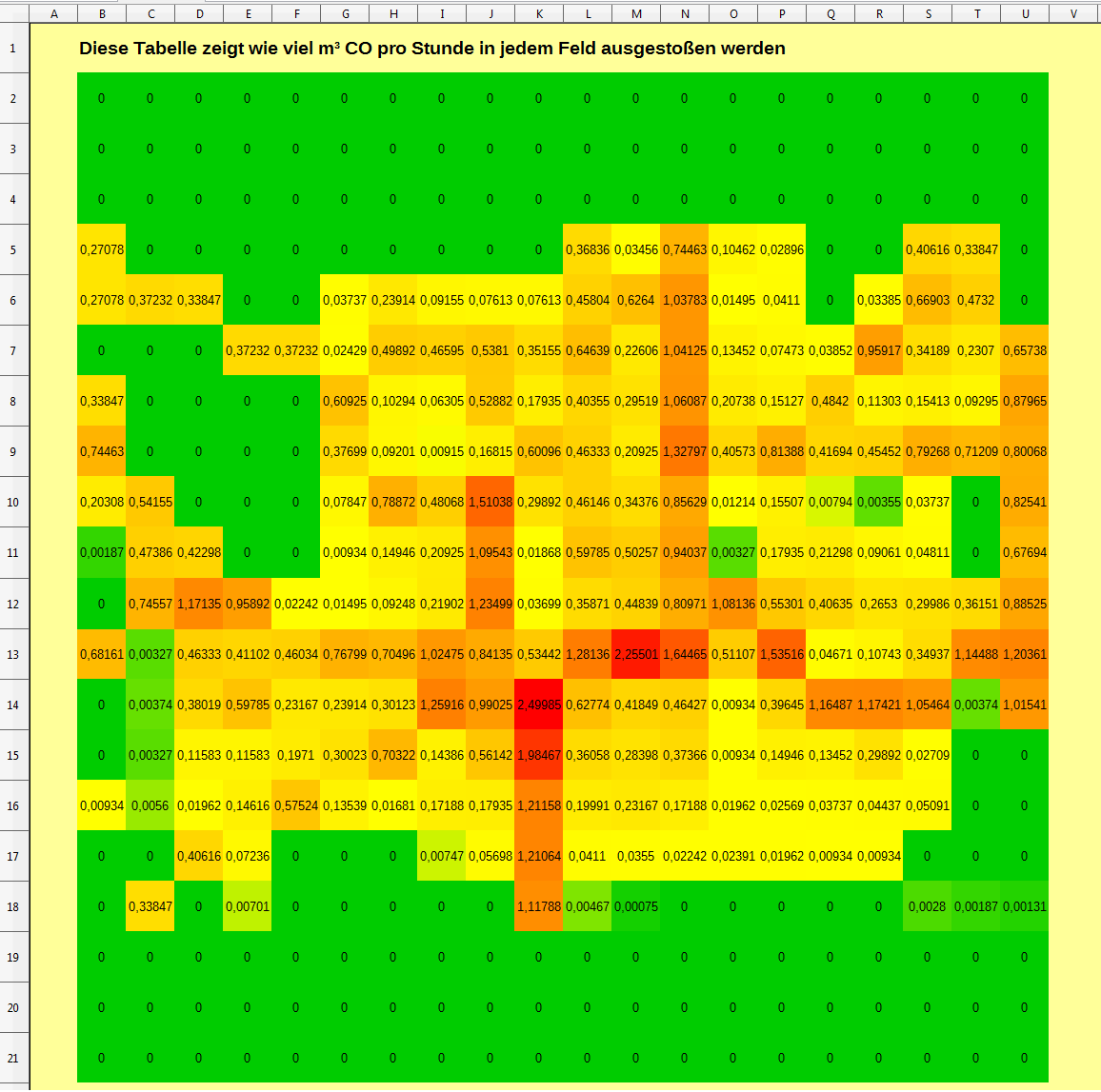
Um die Diffusion von Kohlenstoffmonoxid in Landau in einer Tabellenkalkulation implementieren zu können, wurde zunächst ein 20x20 Raster auf die Stadtkarte gezeichnet, das die Stadt in 400 Felder einteilt (siehe Abbildung). Durch die Beschriftung der Spalten mit Großbuchstaben und der Zeilen mit Zahlen, hat jedes Feld eine eigene Benennung (z.B. befindet sich der Hauptbahnhof in der Zelle N11).

Berechnung der Emission pro Feld und pro Stunde[Bearbeiten]

Benötigte Werte[Bearbeiten]

Straßenbreite und -längen

Wie viel Kohlenstoffmonoxid in einem Feld ausgestoßen wird, hängt von den Straßen ab, die sich in diesem Feld befinden. Die Stadtkarte unterscheidet zwischen breiten, mittleren und schmalen Straßen. Diese Unterscheidung wird in der Modellierung berücksichtigt, da wir davon ausgehen, dass mehr Autos auf einer breiten Straße fahren als auf einer schmalen. Außerdem gilt es zu berücksichtigen, wie lang die Straßen in einem Feld sind. Deshalb wurde für jedes Feld der Stadtkarte ausgemessen, wie viel mm breite, mittlere und schmale Straße es beinhaltet. Die Messungen (in mm) wurden anschließend in der ersten Tabelle der Modellierung eingetragen.

In der zweiten Tabelle der Tabellenkalkulation werden die Messungen mit Hilfe des Maßstabs in die realen Straßenlängen (in m) umgerechnet. Mit diesen Werten wird weitergearbeitet.

Anzahl der Autos pro Stunde

Für die Ermittlung dieser Werte wurde eine Datenerhebung (einstündige Verkehrszählung) an der Kreuzung Hainbachstraße & August-Croissant-Straße durchgeführt. Diese Kreuzung wurde gewählt, um mit nur einer Verkehrzählung zu ermitteln, wie viele Autos auf einer großen Straße (Hainbachstraße) und wie viele auf einer mittleren Straße (August-Croissant Straße) fahren.

von	nach	Anzahl Autos
Hainbachstr.	Hainbachstr.	891
Hainbachstr.	August-Croissant-Str.	166
August Croissant-Str.	August-Croissant	44
August-Croissant-Str.	Hainbachstr.	227

Die Anzahl der Autos, die abgebogen sind, werden in der Modellierung halb zur breiten und halb zur mittleren Straße gezählt.

Gewichtung für das Verkehraufkommen

Eine mittlere Straße, die eine Sackgasse ist oder die sich in einem Wohngebiet befindet, hat weniger Verkehrsaufkommen als die August-Croissant-Straße, die zum Abkürzen genutzt werden kann. Anhand solcher Kriterien werden (in Tabelle 3) für jedes Feld Gewichtungen geschätzt, die das Verkehrsaufkommen in Abhängigkeit zu den „gezählten Straßen“ (Hainbachstraße und August-Croissant Straße) beschreiben. Mit der Gewichtung wird je nach Straße ein niedrigeres oder höheres Verkehraufkommen im Vergleich zu den "gezählten Straßen" modelliert.

Emission pro Auto und pro Meter

Wir interessieren uns hier für die Frage, wie viel CO ein Auto pro gefahrenem Meter ausstößt. Dies kann anhand von Informationen zur Abgas-Zusammensetzung berechnet werden.

Ein Auto stößt pro Liter verbrauchten Benzin $10m^{3}$ Abgase aus.
Von diesen $10m^{3}$ sind bei einem Ottomotor $0,258\%$ Kohlenstoffmonoxid.
Wir nehmen an, dass ein Auto innerorts durchschnittlich $7l/100km$ verbraucht.

Der CO-Ausstoß von einem Auto, das 1km fährt, wird folgendermaßen ausgerechnet:

$7l/{100km}\cdot 10m^{3}/l\cdot 0,258\%/{100}=0,001806m^{3}/{km}$

Daraus ergibt sich für die Emission von einem Auto pro gefahrenem Meter ein Wert von $0,001806m^{3}/{km}/1000=0,000001806m^{3}/m$ .

Formel[Bearbeiten]

Seien

$F$ das Feld
$E_{PKW}$ das Kohlenmonoxid in $m^{3}$ , das ein Auto durchschnittlich pro Meter ausstößt
$SB_{F}$ die Länge der breiten Straßen, die sich im Feld $F$ befinden
$SM_{F}$ die Länge der mittleren Straßen, die sich im Feld $F$ befinden
$SK_{F}$ die Länge der kleinen Straßen, die sich im Feld $F$ befinden
$AB$ die Anzahl der Autos, die pro Stunde auf einer breiten Straße fahren
$AM$ die Anzahl der Autos, die pro Stunde auf einer mittleren Straße fahren
$AK$ die Anzahl der Autos, die pro Stunde auf einer kleinen Straße fahren
$GB_{F}$ die Gewichtung für das Verkehrsaufkommen auf den breiten Straßen im Feld $F$
$GM_{F}$ die Gewichtung für das Verkehrsaufkommen auf den mittleren Straßen im Feld $F$
$GK_{F}$ die Gewichtung für das Verkehrsaufkommen auf den kleinen Straßen im Feld $F$

Die stündliche Emission von Kohlenmonoxid in einem Feld F lässt sich folgendermaßen berechnen:

$E_{PKW}\cdot (GB_{F}\cdot SB_{F}\cdot AB+GM_{F}\cdot SM_{F}\cdot AM+GS_{F}\cdot SS_{F}\cdot AS)$

Die „Emissionsmatrix“[Bearbeiten]

Diese Formel auf jedes Feld angewendet ergibt eine $20\times 20$ -Matrix, die die stündliche Emission in der gesamten Stadt beschreibt.

Durch die farbliche Formatierung ist auf einem Blick zu erkennen, an welchen Stellen viel CO ausgestoßen wird und an welchen Stellen weniger.

Formal

$E={\begin{pmatrix}e_{1,1}&\dots &e_{1,20}\\\vdots &&\vdots \\e_{20,1}&\dots &e_{20,20}\end{pmatrix}}\in Mat(20\times 20,\mathbb {R} )$

Diffusion[Bearbeiten]

Die Modellierung zeigt im Stundentakt, wie sich das CO innerhalb der Stadt verbreitet. Für jeden Zeitpunkt $t$ wurde eine Tabelle angelegt, in der eine Matrix $M_{t}\in (22\times 22,\mathbb {R} )$ das CO-Aufkommen zu diesem Zeitpunkt beschreibt. Die zusätzlichen Zeilen und Spalten werden gebraucht, um einen Rand mit Nullen zu definieren. Diese Randbedingung sorgt dafür, dass das CO sich frei in die Umgebung verteilt und dass von außerhalb der Stadt kein CO rein kommt.

Die Verteilungsmatrix[Bearbeiten]

Es stellt sich zunächst die Frage: Wie viel vom Stoff, der sich in einem Feld befindet, wird nach einer Stunde in die 8 benachbarten Felder verteilt? Dies wurde anhand einer $3\times 3$ -Verteilungsmatrix festgelegt, die wie folgt aussieht:

Formal

$V={\begin{pmatrix}{\sqrt {0,001}}&0,001&{\sqrt {0,001}}\\0,001&0,98455088&0,001\\{\sqrt {0,001}}&0,001&{\sqrt {0,001}}\end{pmatrix}}\in Mat(3\times 3,\mathbb {R} )$

Wir nehmen also an, dass nach einer Stunde ein Prozentsatz von 0,001 in ein direkt benachbartes Feld diffundiert. In die indirekt benachbarten Felder diffundiert jeweils ein Prozentsatz von ${\sqrt {0,001}}$ und im Feld selber bleiben ca. 98,46% des Stoffs. Hierbei handelt es sich allerdings nur um geschätzte Werte. In der nächsten Optimierung des Modells könnte herausgefunden werden, welche Verteilung realistisch wäre.

Besonderheit:

Die Verteilungsmatrix berücksichtigt, dass sich CO auch in der Höhe ausbreitet. Da uns nur das Abgasaufkommen in dem Raum interessiert, in dem sich Menschen bewegen, betrachten wir nur den Stoff, der sich nicht höher als 10m befindet. Deshalb verschwindet jede Stunde ein Anteil (der Anteil von ca. 0,0086, der die 10m Höhe überschreitet).

Diffusion nach 1h[Bearbeiten]

Wir nehmen an, dass es zum Zeitpunkt 0 kein Abgasaufkommen in der Stadt gibt. Dementsprechend ist das Aufkommen von CO nach einer Stunde dasselbe wie in der Emissionsmatrix. Die farbliche Formatierung wurde so gewählt, dass beim Vergleich der Zeitpunkte die Verbreitung möglichst gut zu erkennen ist.

Formal

$M_{1}={\begin{pmatrix}m_{1,1}&\dots &m_{1,22}\\\vdots &&\vdots \\m_{22,1}&\dots &m_{22,22}\end{pmatrix}}\in Mat(22\times 22,\mathbb {R} )$

Die Komponenten am Rand $m_{1,r}$ , $m_{22,r}$ , $m_{r,1}$ und $m_{r,22}$ mit $r=1,2,...,22$ haben wegen der Randbedingung den Wert $0$
Für die inneren Komponenten $m_{z,s}$ mit $z,s\in \{2,3,\dots ,21\}$ gilt: $m_{z,s}=e_{z-1,s-1}$ , wobei $e_{z-1,s-1}$ eine Komponente aus $E\in Mat(20\times 20,\mathbb {R} )$ (Emissionsmatrix) ist.

Diffusion nach weiteren Stunden[Bearbeiten]

Auch jede folgende Matrix $M_{t}\in Mat(22\times 22,\mathbb {R} )$ mit $t\in \{2,3,\dots ,12\}$ und

$M_{t}={\begin{pmatrix}m_{1,1,t}&\dots &m_{1,22,t}\\\vdots &&\vdots \\m_{22,1,t}&\dots &m_{22,22,t}\end{pmatrix}}$

haben Nullen als Randkomponenten.

Seien im Folgenden $z,s\in \{2,3,\dots ,21\}$ beliebig aber fest, die inneren Komponenten $m_{z,s,t}$ sind abhängig von $\dots$

 ... der Komponenten  $e_{z-1,s-1}$  aus der Emissionsmatrix  $E$

 ... der  $3\times 3$ -Verteilungsmatrix  $V={\begin{pmatrix}{\sqrt {0,001}}&0,001&{\sqrt {0,001}}\\0,001&0,98455088&0,001\\{\sqrt {0,001}}&0,001&{\sqrt {0,001}}\end{pmatrix}}={\begin{pmatrix}v_{1,1}&v_{1,2}&v_{1,3}\\v_{2,1}&v_{2,2}&v_{2,3}\\v_{3,1}&v_{3,2}&v_{3,3}\end{pmatrix}}$

 ... einer Teilmatrix  $T_{t-1}\in Mat(3\times 3,\mathbb {R} )$ , deren Komponenten aus der Matrix  $M_{t-1}\in Mat(22\times 22,\mathbb {R} )$  kommen mit  $T_{t-1}={\begin{pmatrix}m_{z-1,s-1,t-1}&m_{z-1,s,t-1}&m_{z-1,s+1,t-1}\\m_{z,s-1,t-1}&m_{z,s,t-1}&m_{z,s+1,t-1}\\m_{z+1,s-1,t-1}&m_{z+1,s,t-1}&m_{z+1,s+1,t-1}\end{pmatrix}}$

Die inneren Komponenten $m_{z,s,t}$ sind das Summenprodukt aus $V$ und $T_{t-1}$ addiert mit $e_{z-1,s-1}$ . Dabei multipliziert das Summenprodukt "die einander entsprechenden Komponenten der angegebenen Matrizen miteinander und gibt die Summe dieser Produkte zurück".^[1]

Ergebnis[Bearbeiten]

Modellierung mit Octave[Bearbeiten]

Ziele[Bearbeiten]

Aufbauend auf den empirisch ermittelten Daten zum Verkehrsaufkommen und der Straßenlängen, die bereits in der Tabellenkalkulation benutzt wurden, sind die Ziele mit dem Einsatz der Open-Source-Software Octave zum einen die Implementierung der physikalischen Gesetzmäßigkeiten der Diffusion und zum anderen weitere Darstellungs- und Veranschaulichungsmöglichkeiten des Projekts zu erschließen, sowie eine Skalierung der Berechnungen zu vereinfachen, sodass eine Anwendung auf ein anderes Problem mit anderen Parametern (z.B. Beobachtungszeitraum, Beobachtungsgebiet...) ermöglicht wird.

Prozess[Bearbeiten]

Die Basis des in Octave arbeitenden Skripts ist also in erster Linie die physikalische Diffusionsgleichung.

\partial _{t}u(x,t)-c\Delta u(x,t)+{\vec {v}}\cdot \nabla u(x,t)=0.

Wobei für unseren Fall gilt, dass die rechte Seite der Gleichung nicht $0$ ist. Diese Seite stellt die sogenannte Quelle dar, was im Kontext des Projektes die Fahrzeuge auf den landauer Straßen sind. Ein weiterer Punkt, den wir für den Modellierungsprozess anpassen mussten war der, dass wir anstatt mit $u(x,t)$ als der Konzentration von Kohlenmonoxid pro Liter pro Qudrat mit der Emission von Kohlenmonoxid in Milligramm pro Quadrat gerechnet haben. Dies liegt darin begründet, dass die Angaben, die man in der Literatur zum CO-Ausstroß eines Verbrennungsmotors findet, üblicherweise in der Einheit Gramm pro gefahrenem Personenkilometer angegeben sind. Die Chemie liefert jedoch eine Gleichung zur Umrechnung von Masse in Stoffmenge. Außerdem haben wir uns auf die 2-dimensionale Betrachtung von Landau beschränkt, da wir zum einen ein Gebiet von 7km auf 7km untersuchen und gleichzeitig bei flacher Topographie Landaus die CO-Werte oberhalb der Höhe eines üblichen Gebäudes eine untergeordnete Rolle bei der Betrachtung spielen.

Die Parameter von denen nun also unsere Berechnungen abhängen sind:

die durchschnittliche CO-Emission eines PKW pro gefahrenem Meter
die Länge der zurückgelegten Strecke eines PKW in einem vorgegebenen Raster-Quadrat (siehe Tabellenkalkulation)
die Anzahl der Autos die im Schnitt auf den unterschiedlichen Straßen Landaus fahren (siehe Tabellenkalkulation)
die Länge des Beobachtungszeitraumes
die Länge der maximalen Ausdehnung des Gebiets (7x7km)
der Diffusionskoeffizient von Kohlenmonoxid in Luft unter Normalbedingungen (0.0000177 m²/s)
die Geschwindigkeit und Richtung des Windes der über Landau weht

Aufgabe des Octave Skriptes ist es den Wert für $u(x,t)$ für einen vorgegebenen Zeitraum zu berechnen. Beginnend mit der Fixierung dieser 7 Parameter wurde das Octave-Skript wiefolgt angelegt.:

 function [Konz_matrix] = DiffusionLD(RasterDimension,Uhrzeitstart,Uhrzeitende,Stroemungx, Stroemungy)

Mit dem Befehl >>DiffusionLD(20,6,12,1000,1000) ruft man die Funktion beispielsweise auf. Sie berechnet dann auf einem 20x20 Raster die Emissionswerte zwischen 6 und 12 Uhr bei einem Wind in X- und Y-Richtung von 1000 Meter pro Stunde und gibt diese in einer Variablen, Konz_matrix, wieder zurück.

 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Parameterfixierung %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 D = RasterDimension;         % Umbenennung
 Us = Uhrzeitstart;           % Umbennenung
 Ue = Uhrzeitende;            % Umbenennung
 wx= Stroemungx;              % Umbenennung Stroemung in Meter pro Stunde
 wy= Stroemungy;              % Umbenennung Stroemung in Meter pro Stunde 
 dimx=7000;                   % Anzahl Zeilen der Matrix
 dimy=7000;                   % Anzahl Spalten der Matrix
 Skalax= dimx/D;              % Skalierung der X-Achse
 Skalay= dimy/D;              % Skalierung der Y-Achse
 Autozahlk=30;                % Anzahl der Autos auf kleinen Straßen pro Stunde
 Autozahlm=240;               % Anzahl der Autos auf mittleren Straßen pro Stunde
 Autozahlg=1087;              % Anzahl der Autos auf großen Straßen pro Stunde
 Auslast = 1.5;               % PKW Auslastung in Personen pro Fahrzeug
 COAusstoss= 0.6*Auslast;     % CO-Ausstoß eines PKW in Milligramm pro Meter
 t=ceil((Ue)-(Us));           % Zeitdauer in vollen Stunden         
 deltaZeit = 1;               % Länge der Einzelnen Zeitschritte
 Uhrs = round(Us);            % Startuhrzeit (volle Stunde)
 fuhr= [0.05 0.05 0.05 0.05 0.1 0.6 0.9 1.7 1.2 1 0.9 1.5 1.1 0.9 1 1 1.2 1.6 1.3 0.9 0.8 0.6 0.3 0.2]; %Faktor für Verkehrsaufkommen
 a= (1.77*10^(-5)*3600)/(Skalax)^2;    % Diffusionskoeffizient

Beim Aufrufen der Funktion werden also die 5 Paramter RasterDimension, Uhrzeitstart, Uhrzeitende, Stroemungx und Stroemungy benötigt, wohingegen die Parameter der Ausdehnung des Gebiets (7000x7000 Meter), die Anzahl der Fahrzeuge auf den unterschiedlichen Straßen Landaus (30,240,1087), der durchschnittliche CO-Ausstoß eines PKW (0.6 mg/m), sowie der Diffusionskoeffizient a=0.0000177 m²/s feste Parameter sind, die zur Berechnung unverändert bleiben.

Erwähnt werden sollte hier noch der Wert "fuhr". Es handelt sich hier um einen Vektor mit 24 Einträgen. Je nachdem welche Uhrzeiten man als Betrachtungszeitraum beim Aufrufen der Funktion angibt, nimmt das Skript den entsprechenden Eintrag (1Uhr = 1. Vektoreintrag) und nutzt diesen als Faktor der mit den Anzahl der Autos multipliziert wird, die zu der angegebenen Uhrzeit auf den Straßen fahren. Fixpunkt, und daher mit dem Vektoreintrag=1, ist der Beobachtungszeitraum der Kreuzung Hainbachstraße & August-Croissant Straße am Montag des 20. Mai 2019 von 14:47 - 15:48 Uhr. Die übrigen Einträge sind Schätzwerte, können aber bei umfassenderen empirisch erhobenen Daten angepasst werden, um ein realistischeres Modell zu erhalten.

Im nächsten Schritt wurde eine Matrix erstellt die den Laplace-Operator $\Delta$ darstellt. Zusätzlich wurde der Diffusionskoeffizient und die Länge eines Raster-Quadrats in den Laplace-Operator mit eingebunden.

 L= diag(-4*ones(1,(D*D)),0)+diag(ones(1,(D*D)-1),-1)+ diag(ones(1,(D*D)-1),1)+diag(ones(1,(D*(D-1))),-D)+ diag(ones(1,(D*(D-1))),D);
 for  i=1:(D-1);      % Fülle Matrixeintrag (i+1,j) und (i, j+1) des
   L(i*D+1,i*D)=0;    % Laplace - Operators mit 0 damit auch tatsächlich eine
   L(i*D,i*D+1)=0;    % Blockmatrix entsteht
 endfor
 
 La= (a/Skalax^2).*L; % Laplace-Operator mit Diffusionskoeffizient und Knotenabständen

Im weiteren Verlauf musste diese Block-Matrix derart abgeändert werden, dass die Windgeschwindigkeiten in x- und y-Richtung berücktsichtigt wurden. Dies wurde mittels mehrerer If-Bedingungen realisiert die unterscheiden aus welcher Richtung der Wind kommt. Je nachdem welche If-Bedingung erfüllt ist füllt dieser Teil des Skripts die System-Block-Matrix an den entsprechenden Ober-bzw. Unterdiagonalen die Matrixeinträge mit 1 bzw. -1.

 if wx>0                  % Fall: Wind in x-Richtung positiv
   Matx=(wx/-Skalax)*(diag(-1*ones(D*D,1),0)+diag(ones(D*D-1,1),-1));
 else                      % Fall: Wind in x-Richtung negativ
   Matx=(wx/Skalax)*(diag(-1*ones(D*D,1),0)+diag(ones(D*D-1,1),1));
 end
 
 for  i=1:(D-1)            %
     Matx(i*D+1,i*D)=0;    % Korrektur von Matx zur Blockmatrix Matx
     Matx(i*D,i*D+1)=0;    %
 endfor
 
 if wy>0                   % Fall: Wind in y-Richtung positiv
   Maty=(wy/-Skalay)*(diag(-1*ones(D*D,1),0)+diag(ones(D*D-D,1),-D));
 else                      % Fall: Wind in y-Richtung negativ
   Maty=(wy/Skalay)*(diag(-1*ones(D*D,1),0)+diag(ones(D*D-D,1),D));
 end

 La=La-Matx-Maty;                % Anpassung der Systemmatrix mit Konvektion

Bevor nun die rechte Seite der Gleichung behandelt werden konnte, musste zuerst noch eine Randbedingung geschaffen werden, damit das Skript weiß wie es die Werte am Rand des Gebiets verteilen darf. Hier haben wir uns für die sogennante Neumann-Randbedingung entschieden, die dafür sorgt, dass zwar aus dem Gebiet hinausverteilt werden darf, aber das "Konzentrationsgefälle" von Randpunkt und Außerhalb gleich 0 ist. Auch in diese Schritt wird die System-Blockmatrix dergestalt abgeändert, dass Sie diese Bedingung erfüllt.

% Neumann RB für y:   a* partial_y u=0   - einzelne Blöcke der Matrix ersetzen
   
 Matnm=diag((a/Skalay)*ones(D,1));
 La(1:D,1:D)=Matnm;
 La(1:D,D+1:2*D)=-Matnm;
 La(D*(D-1)+1:D*D,D*(D-1)+1:D*D)=Matnm;
 La(D*(D-1)+1:D*D,D*(D-2)+1:D*(D-1))=-Matnm;
 
 % Neumann RB für x:   a* partial_x u=0 - einzelne Zeilen der Matrix ersetzen
 
 for i=0:(D-1)
   neumxtop=zeros(1,D*D);
   neumxtop(D*i+1)=a/Skalax;
   neumxtop(D*i+2)=-a/Skalax;
   
   neumxbot=zeros(1,D*D);
   neumxbot(D*i+D)=a/Skalax;
   neumxbot(D*i+D-1)=-a/Skalax;
   
   La(i*D+1,:)  =neumxtop;       % Anpassung der Systemmatrix mit Neumann RB
   La(i*D+D,:)  =neumxbot;       % Anpassung der Systemmatrix mit Neumann RB
 endfor

Im vorletzten Schritt wurde dann die Quelle so definiert wie sie in der Tabellenkalkulation auch definiert wurde. Allerdings wurden hier weitere Variablen integriert. So ist die Quelle im Ocataveskript im Gegensatz zur Tabellenkalkulation uhrzeitabhängig und abhängig von der gewählten Feingliedrigkeit des Rasters. Beispielhaft seien hier nur 2 Zeilen des Codes zur Quelle aufgeführt um die Logik dahinter nachvollziehen zu können. Erstellt wurde eine Matrix, die die gleiche Dimension des Rasters hat und anschließend die entsprechenden Matrixeinträge so abändert, dass Sie dem Raster der Tabellenkalkulation entsprechen.

Mit dem Befehlt Quelle(i,j) spricht man den Eintrag der Matrix mit den Indizes i,j an. Diese wurden dann entsprechend der, in der Tabellenkalkulation, verwendeten Formel mit einem Wert gleichgesetzt. Zusätzlich wurde ein Faktor ans Ende gesetzt, der die Uhrzeit berücksichtigt. Die Schwierigkeit bestand zudem darin, dass die Tabellenkalkulation auf einem festen 20x20 Raster operiert. Das Octave-Skript sollte aber auch mit einer anderen Rasterung rechnen dürfen. Hierfür ist die häufige Verwendung von "D" im Term nötig. Dieser gibt die Rastergröße an und somit skaliert die Quelle mit der Rasterung.

 Quelle(floor(3*D/20)+1:floor(4*D/20),1:floor(1*D/20))=(Autozahlk*COAusstoss*0+Autozahlm*COAusstoss*0+Autozahlg*COAusstoss*68.9656)*fuhr(Uhrs+(k-1))/(D/20)^2;    
 Quelle(floor(3*D/20)+1:floor(4*D/20),floor(10*D/20)+1:floor(11*D/20))= (Autozahlk*COAusstoss*0+Autozahlm*COAusstoss*275.862+Autozahlg*COAusstoss*344.828)*fuhr(Uhrs+(k-1))/(D/20)^2;

Da nun alle Unbekannten, bis auf $u(x,t)$ , der Diffusionsgleichung ermittelt sind, ist nurnoch einen Auswertung der eingegebenen Parameter notwendig. Abschließend wird die Ergebnismatrix mit der Befehl "surf()" geplottet und als neue Ausgangsmatrix im nächsten Zeitschritt benutzt. Dieses Lösungsverfahren nennt man implizit.

 f= reshape(Quelle,D*D,1);          %Quelle-Matrix als Spaltenvektor
 
 Konzneu=Konz;                      % neue Variable Konzneu = Konz
 
 I=eye(D*D);                        % Einheitsmatrix (D*D)x(D*D)
 Konzneu =(I-deltaZeit*La)\(deltaZeit*f+Konz);   % Lösung der Poisson-Gleichung
 Konz_matrix=reshape(Konzneu,D,D);  % Transformiere Lösungsvektor zur Matrix DxD
 figure(k);                         % Speicherung in einzelnem Plot
 surf(x,y,Konz_matrix);             % Plotte Konzentrations-Matrix
 title("CO-Ausbreitung in LD")      % Titel des Plots
 xlabel("Ost-West")                 % X-Achsen Bennenung
 ylabel("Süd-Nord")                 % Y-Achsen Bennenung
 colormap(jet);                     % Änderung der Farbgebung
 Konz=Konzneu;                      % Neue Konz-Matrix
 
 endfor
 endfunction

Ergebniss[Bearbeiten]

Hier sind die beiden Plots für den Befehl >> DiffusionLD(90,1,24,1000,1000). D.h. eine Rastergröße von 90x90, in einem Zeitraum von 1-24 Uhr und einem Wind aus Süd-Ost-Richtung von ca. 1,5km/h.

Auf der linken Seite der 2-dimensionale Plot und auf der rechten Seite der 3-dimensionale Plot.

Ergebnisrelexion[Bearbeiten]

Da die beiden Plots zueinander passen lässt sich eine Verbindung herstellen und so kann man die Vorteile beider Plots ausnutzen, um zusätzliche Informationen zu erhalten


	Vorteile	Nachteile
2D-Plot	Einfluss des Windes auf die Schadstoffverteilung leicht erkennbar Verknüpfung zwischen Ort und Schafstoffexposition sehr einfach	Aussage über die absoluten Expositionswerte nicht möglich Kein raltiver Bezug zwischen absoluter Schaffstoffexposition verschiedener Uhrzeiten möglich
3D-Plot	Leichter relativer Bezug zwischen absoluter Schadstoffexposition verscheidener Uhrzeiten Absolute Schadstoffexposition zu jeden Zeitschritt ablesbar	Verknüpfung zwischen Ort und Schadstoffbelastung schwierig

Was man an den Plots gut erkennen kann ist, dass erst ab 6 Uhr früh der Ausstoß von Kohlenmoxid wirklich relevant ansteigt. Durch den Wind und die Diffusion in der Luft glättet sich die Kurve bis in den Mittagsstunden. Zu den Rush-Hour Zeiten zwischen 12-13 Uhr und auch wieder zwischen 17-18 Uhr sieht man aber wie die Kurve wieder neue "Zacken" bekommt, da in kurzer Zeit große Emissionszuwächse stattfinden. Außerdem sieht man auch, dass ab 21 Uhr aufgrund des geminderten Verkehrsaufkommens die Kurve wieder beginnt zu sinken, da das Kohlenmonoxid in die Umgebung diffundiert bzw. mit dem Wind aus dem Beobachtungsgebiet getragen wird.

↑ http://www.excelmexel.de/HTMLExcel/summenprodukt.htm

[1] ttp://www.excelmexel.de/HTMLExcel/summenprodukt.htm

[1]