Ganze Zahlen/Konstruktion aus natürlichen Zahlen/Beispiel
Es sei die Menge der natürlichen Zahlen und die Produktmenge mit der komponentenweisen Addition. Wir erklären auf eine Relation durch
Dies ist bei genau dann der Fall, wenn es ein (nämlich ) mit
gibt. D.h. die beiden Paare unterscheiden sich um ein Diagonalelement, also um ein Paar, wo beide Komponenten übereinstimmen. Diese Relation ist eine Äquivalenzrelation auf , siehe Aufgabe. Wenn man als ein quadratisches Gitter anordnet (das ist ein „diskretes Koordinatensystem“), so sind die Äquivalenzklassen durch die Punkte auf einer zur Diagonalen parallelen „diskreten Geraden“ gegeben. Die Punkte mit sind äquivalent zu , sie haben also einen Repräsentanten, bei dem die zweite Komponente ist. Die Punkte mit sind äquivalent zu , sie haben also einen Repräsentanten, bei dem die erste Komponente ist. Die Punkte sind zu äquivalent. Den Repräsentanten einer Äquivalenzklasse, bei dem mindestens eine Komponente ist, nennen wir den Standardvertreter dieser Äquivalenzklasse. Die Standardvertreter sind die diskreten Punkte des begrenzenden Viertelkreuzes; zu einem Punkt ergibt sich der Standardvertreter, wenn man parallel zur Diagonalen in Richtung der Halbachsen wandert, bis man auf einer der Halbachsen landet. Zwei Punkte sind genau dann äquivalent, wenn sie den gleichen Standardvertreter besitzen.
Wir bezeichnen nun die Quotientenmenge, also die Menge der Äquivalenzklassen unter dieser Äquivalenzrelation, als Menge der ganzen Zahlen und bezeichnen sie mit . Jede ganze Zahl hat dann genau einen Standardvertreter der Form mit , der Form oder der Form mit . Eine natürliche Zahl fassen wir von nun an als die ganze Zahl auf.
Wir wollen nun zwei ganze Zahlen, also zwei solche Äquivalenzklassen und miteinander „addieren“, also eine Verknüpfung auf einführen. Der naheliegende Ansatz ist, diese Verknüpfung mittels der komponentenweisen Addition als
zu definieren. Hier tritt das Problem der Wohldefiniertheit auf, denn die Verknüpfung wird erklärt unter Bezug auf Repräsentanten, und es ist nicht von vornherein klar, dass unterschiedliche Repräsentanten zum gleichen Ergebnis führen. Wenn also und sind, so muss man überprüfen, dass
und damit ist. Dies ist der Fall, siehe Aufgabe. Man kann weiterhin zeigen, dass die so definierte Verknüpfung auf assoziativ und kommutativ ist, dass das neutrale Element der Verknüpfung ist und dass es zu jedem Element ein inverses Element gibt, nämlich .
Wir definieren nun eine Multiplikation auf durch
Dies ist wieder wohldefiniert und man kann zeigen, dass die Multiplikation assoziativ und kommutativ ist mit als neutralem Element und dass das Distributivgesetz gilt.

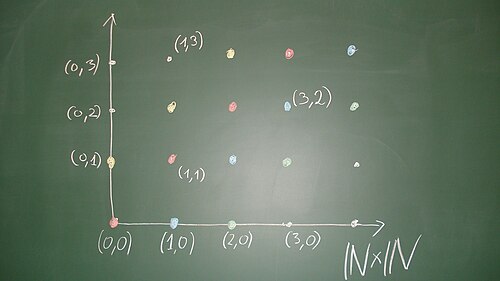
























![{\displaystyle {}[(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad856e5411d0b9ea10ddb04a48932aef19892e7a)
![{\displaystyle {}[(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b865712c6f9654641f6315839d7fb250d5ed6fa1)

![{\displaystyle {}[(a,b)]\oplus [(c,d)]:=[(a+c,b+d)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a778629177dd8a896f6ce8cb000f41b321dc395)



![{\displaystyle {}[(a+c,b+d)]=[(a'+c',b'+d')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b9bc368eabf53b7c89081c97a70ea09b665f4fb)
![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9)
![{\displaystyle {}[(b,a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7257885d4524a38fea17a5ad720d33f256cdeaf8)
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e886953fa3c1d350ffa773ec3c5eee3948d2a80c)
![{\displaystyle {}1=[(1,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7def7a0131953ef73e591cb841fb440c9b19b53b)