Gradientenabstiegsverfahren

Einführung

Das Gradientenverfahren, auch Verfahren des steilsten Abstiegs genannt, ist ein Verfahren, das in der Numerik eingesetzt wird, um allgemeine Optimierungsprobleme zu lösen. Dabei geht man (am Beispiel eines Minimierungsproblems) von einem Näherungswert aus. Von diesem schreitet man in Richtung des negativen Gradienten (der die Richtung des steilsten Abstiegs von diesem Näherungswert angibt) fort, bis man keine numerische Verbesserung mehr erzielt.^[1]

Animation

Bemerkung - Animation

In der Animation werden Startpunkte in ein rechteckigen Gitter schachbrettmusterartig in dem Definitionsbereich verteilt. Jede Einzelbewegung dieser Punkte stellt einen Gradientenabstieg dar. Wenn der Gradientenabstieg gegen ein lokale Minimum konvergiert, so muss das nicht das absolute Minimum (z.B. von einer Fehlerfunktion/Kostenfunktion) sein. Wenn man die Startpunkte gitterartig im Definitionsbereich verteilt, findet man ggf. mehrere lokale Minima und wählt dann in einem letzten Optimierungsschritte die Stelle aus, die den geringsten Wert der Zielfunktion (Fehlerfunktion oder Kostenfunktion) besitzt.

Wiki2Reveal-Folien

Diese Seite zum Gradientenabstiegsverfahren ist zugleich ein Wik2Reveal-Foliensatz .

CAS4Wiki - Partielle Ableitung

Diese Lernressource enthält CAS4Wiki-Testlinks zur

Berechnung von partiellen Ableitung mit folgendem CAS4Wiki-Startlink für partielle Ableitungen

Bemerkung Konvergenz

Das Verfahren konvergiert oftmals sehr langsam, da es sich dem OptimuÏm mit einem starken Zickzack-Kurs nähert. Für die Lösung von symmetrisch positiv definiten linearen Gleichungssystemen bietet das Verfahren der konjugierten Gradienten hier eine immense Verbesserung. Der Gradientenabstieg ist mit dem Bergsteigeralgorithmus (hill climbing) verwandt.

Das Optimierungsproblem

Das Gradientenverfahren ist einsetzbar, wenn es um die Minimierung einer reellwertigen, differenzierbaren Funktion $f:\mathbb {R} ^{n}\rightarrow \mathbb {R}$ geht; also um das Optimierungsproblem

{\underset {x\in \mathbb {R} ^{n}}{\rm {min}}}\ f(x).

Hierbei handelt es sich um ein Problem der Optimierung ohne Nebenbedingungen, auch unrestringiertes Optimierungsproblem genannt.

Wesentliche Schritte

Gradient zeigt in die Richtung der "stärksten" Steigung.
der negative Gradient zeigt daher in die Richtung, in der die Funktionswerte von $f$ fallen.
Es kann passieren, dass man bei einem Iterationsschritt über das lokale Minimum der Funktion $f$ hinwegspringt. Dann würde man die Schrittweite entsprechend verkleinern, um den Funktionswert von $f$ weiter zu minimieren und genauer zu approximieren.

Abbruchbedingung

Abbruchbedingung für das Gradientabstiegsverfahren wäre, wenn wir mit der Iteration eine Stelle $x^{(k)}\in \mathbb {R} ^{n}$ gefunden haben an der der Gradient von $f$ 0 ist

\operatorname {Grad} (f)(x^{(k)})=0\in \mathbb {R} ^{n}

.

Allgemein ist der Gradient einer Stelle $x^{(k)}\in \mathbb {R} ^{n}$ für den $k$ -ten Iterationsschritt wie folgt über die partiellen Ableitungen definiert:

\operatorname {Grad} (f)(x^{(k)}):=\left({\frac {\partial f}{\partial x_{1}}}(x^{(k)}),\cdots ,{\frac {\partial f}{\partial x_{n}}}(x^{(k)})\right)

Notation

Es wird die englische Notation für den Dezimalpunkt statt Komma verwendet. Dies wird analog zu Computer-Algebra-Systemen gemacht, damit die Trennung zwischen Komponenten in einem $n$ -Tupel auch mit Zahlen möglich ist. $(6,5)\in \mathbb {R} ^{2}$ ist ein Vektor mit zwei Komponenten. Besitzen die Komponenten des Vektors Nachkommastellen, werden diese mit einem Punkt notiert - z.B. $(6.12\,,\,5.898)\in \mathbb {R} ^{2}$

Beispiel für einen Gradienten

Sei $f(x_{1},x_{2}):=x_{1}^{3}\cdot x_{2}+x_{2}^{2}$ :

{\begin{array}{rcl}\operatorname {Grad} (f)(x_{1},x_{2})&=&\left({\frac {\partial f}{\partial x_{1}}}(x_{1},x_{2}),{\frac {\partial f}{\partial x_{2}}}(x_{1},x_{2})\right)\\&=&\left(3x_{1}^{2}x_{2}\,,\,x_{1}^{3}+2x_{2}\right)\\\end{array}}

Damit können wir den Gradienten an eine bestimmten Stelle im Definitionsbereich berechnen:

\operatorname {Grad} (f)(1,2)=(6,5)

CAS4Wiki

Mit CAS4Wiki können Sie die obigen Ableitung berechnen, siehe z.B. partielle Ableitungen

Beispiel - normierter Gradienten

Mit einem vom Nullvektor verschiedenen Gradienten $\operatorname {Grad} (f)(1,2)=(6,5)$ kann man einen normierten "negativen" Gradienten erzeugen:

d^{(j)}:=-{\frac {\operatorname {Grad} \left(f(1,2)\right)}{\left\|\operatorname {Grad} \left(f(1,2)\right)\right\|}}={\frac {(-6,-5)}{\sqrt {36+25}}}=\left(-{\frac {6}{\sqrt {61}}},-{\frac {5}{\sqrt {61}}}\right)

Das Verfahren

Als Einführung in das Gradientenabstiegsverfahren wird eine vereinfachte Schrittweitenberechung verwendet.

Das Verfahren bricht ab, wenn der Gradient der Nullvektor ist.
Ist der Gradient nicht der Nullvektor, wird der negative Gradient zunächst auf die Länge 1 normiert und mit der Schrittweite $\alpha _{j}$ multipliziert.
Die Schrittweite wird halbiert, wenn nach dem Iterationsschritt der Funktionwert (z.B. Kosten) nicht abnehmen.
Eine weitere Abbruchbedingung für die Iteration ist, wenn die Schrittweite eine Genauigkeitsgrenze $\varepsilon >0$ unterschreitet (d.h. $\alpha _{j}<\varepsilon$ ).

Start der Optimierung

Als Anfangspunkt wird eine Stelle $x^{(0)}$ aus dem Definitionsbereich der Funktion $f$ ausgewählt, für die man lokale Minima mit dem Gradientenabstiegsverfahren annähern möchte.

Richtung des steilsten Abstiegs

Ausgehend von einem Anfangspunkt $x^{(0)}$ bzw. von der aktuelle Stelle $x^{(j)}$ für den nächsten Iterationsschritt wird die Richtung des steilsten Abstiegs durch $-\operatorname {Grad} \left(f(x^{(j)})\right)$ bestimmt, wobei $\operatorname {Grad} \left(f(x^{(j)})\right)\in \mathbb {R} ^{n}$ den Gradienten von $f$ an der Stelle $x^{(j)}\in \mathbb {R} ^{n}$ bezeichnet. Dieser zeigt in die Richtung des "größten Anstiegs". Das negative Vorzeichen vor dem Gradienten sorgt dafür, dass man sich mit den Iterationsschritten in die Richtung des stärksten Abfalls bewegt (z.B. Minimierung der Kostenfunktion/Fehlerfunktion $f$ ).

Normierung des Richtungsvektors

Das vereinfachte Interationsverfahren bricht bei der Bedingung ab, wenn $\left\|\operatorname {Grad} \left(f(x^{(j)})\right)\right\|<\varepsilon$ . Ansonsten wird der Richtungsvektor für den folgenden Iterationsschritt normiert (dies ist optional, um die Schrittweite im Lernalgorithmus zu normalisieren) :

d^{(j)}:=-{\frac {\operatorname {Grad} \left(f(x^{(j)})\right)}{\left\|\operatorname {Grad} \left(f(x^{(j)})\right)\right\|}}

mit Euklidischer Norm

\|x\|:=\|(x_{1},\ldots ,x_{n})\|:={\sqrt {\sum _{k=1}^{n}x_{k}^{2}}}

Iterationsschritt

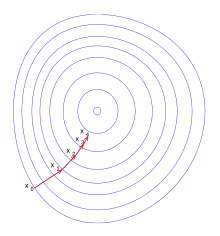
Formal notiert man diesen Iterationsschritt wie folgt:

x^{(j+1)}={\begin{cases}x^{(j)}+\alpha ^{(j)}d^{(j)},&{\text{wenn }}f(x^{(j)}+\alpha ^{(j)}d^{(j)})<f(x^{(j)}){\text{ }}{\text{ (Verbesserung) }}\\x^{(j)},&{\text{sonst }}\end{cases}}

Wenn keine Verbesserung vorliegt, wird die Schrittweite verkleinert (z.B. halbiert).

Festlegung der Schrittweite

Die Schrittweite wird so lange für den nächsten Iterationsschritt verwendet, bis sich die Kostenfunktion $f$ mit dem nachfolgende Schritt erhöht. In diesem einführenden Beispiel wird die Schrittweite $\alpha ^{(j)}$ halbiert. Formal

\alpha ^{(j+1)}={\begin{cases}\alpha ^{(j)},&{\text{wenn }}f(x^{(j)}+\alpha ^{(j)}d^{(j)})<f(x^{(j)}){\text{ (Verbesserung) }}\\{\frac {\alpha ^{(j)}}{2}},&{\text{sonst }}\end{cases}}

Alternative Schrittweitenverkleinerung

Die Schrittweitenverkleinerung kann allgemein auch durch einen Faktor $\delta$ mit $0<\delta <1$ über

\alpha ^{(j+1)}:=\alpha ^{(j)}\cdot \delta

ersetzt werden.

Schrittweitenfestlegung pro Iterationsschritt

Dabei ist $\alpha ^{(j)}>0$ die Schrittweite im j-ten Iterationschritt. Diese Schrittweite muss in jedem Schritt des Iterationsverfahrens bestimmt werden. Hierfür gibt es im Allgemeinen unterschiedliche Möglichkeiten, wie die Rückführung der Schrittweitenbestimmung auf ein eindimensionales Optimierungsproblem. Die hier gewählte Schrittweitenoptimierung ist als Einführung in das Thema gewählt worden.

Gradientenabstieg in Tabellenkalkulation

In der folgenden ZIP-Datei von GitHub befindet sich eine LibreOffice-Datei mit einem exemplarischen Gradientenabstieg für die Kostenfunktion:

f(x_{1},x_{2}):=\sin(x_{1})+\cos(x_{2})+3

.

Die Kostenfunktion hat auf ihrem Definitionsbereich $\mathbb {R} ^{2}$ unendlich viele lokale Minima. Das Minimum der Kostenfunktion ist nach Definition -1. In jeder Tabellenzeile wird ein Iterationsschritt durchgeführt und überprüft, ob die Kostenfunktion nach dem Iterationsschritt tatsächlich abnimmt.

Rückführung auf ein eindimensionales Optimierungsproblem

Eine Methode besteht darin, $\alpha ^{(j)}$ durch die Minimierung der Funktion auf dem (eindimensionalen) "Strahl" $x^{(j)}(\alpha )$ zu bestimmen, der ausgehend von $x^{(j)}$ in Richtung des negativen Gradienten zeigt. Die eindimensionale zu minimierende Funktion $M$ ist wie folgt definiert.

M:\mathbb {R} ^{+}\rightarrow \mathbb {R} ,\qquad \alpha \mapsto M(\alpha ):=f\left(x^{(j)}(\alpha )\right)f\left(x^{(j)}+\alpha d^{(j)}\right)

mit

x^{(j)}(\alpha )=x^{(j)}+\alpha d^{(j)}.

Man berechnet in diesem Fall das $x^{(j+1)}:=x^{(j)}(\alpha _{o})$ mit $\alpha _{o}>0$ so, dass $M(\alpha _{o})$ minimal wird. d.h.:

f\left(x^{(j+1)}\right)={\underset {\alpha >0}{\min }}\ {f\left(x^{(j)}(\alpha )\right)}.

Dies ist ein einfaches, eindimensionales Optimierungsproblem, für das es spezielle Verfahren der Schrittweitenbestimmung gibt.

Schrittweiten und iterierte Schrittweitenverkleinerung

Eine andere Methode besteht darin, $\alpha ^{(j)}$ von der Minimierung der Funktion $f$ abhängig zu machen, d. h. von der Bedingung $f(x^{(j+1)})<f(x^{(j)})$ . Wird mit dem Iterationsschritt der Funktionswert mit einer Startschrittweite $\alpha _{0}>0$ nicht vermindert, verkleinert man die Schrittweite z. B. mit $\alpha _{k+1}:=\alpha _{k}\cdot s$ mit $0<s<1$ weiter, bis die Schrittweite ausgehend von $x^{(j)}$ in Richtung des negativen Gradienten tatsächlich einen Funktionswert $f(x^{(j)}+\alpha _{k}d^{(j)})<f(x^{(j)})$ liefert und setzt $x^{(j+1)}=x^{(j)}+\alpha _{k}d^{(j)}$ .

Hat man im Iterationsverfahren eine Stelle $x^{(j+1)}\in \mathbb {R} ^{n}$ mit $\operatorname {Grad} \left(f(x^{(j+1)})\right)=\mathbf {0} \in \mathbb {R} ^{n}$ erreicht, liegt eventuell eine lokale Extremstelle von $f$ vor (Überprüfung bzw. Abbruch des Iterationsverfahrens).

Abbruchbedingung

Ein zentrales Kriterium für eine Abbruchbedingung ist, dass $d^{(j)}=-\operatorname {Grad} \left(f(x^{(j)})\right)=\mathbf {0} \in \mathbb {R} ^{n}$ ist.

Sattelpunkt/Sattelfläche

Wie in der reellen eindimensionalen Analysis muss sich an dieser Stelle $x^{(j)}\in \mathbb {R} ^{n}$ keine lokales Minimum befinden (eindimensional Sattelpunkt, mehrdimensional z.B. Sattelfläche). Wenn für $f:U\rightarrow \mathbb {R}$ zweimal stetig differenzierbar ist und die Hesse-Matrix an dieser Stelle positiv definit ist, liegt in $x^{(j)}\in \mathbb {R} ^{n}$ hinreichendes Kriterium für ein lokales Minimum. Dieses wird ausgegeben und die Iteration abgebrochen.

Schrittweite als Abbruchbedingung

Wird der Algorithmus auf einem Computer ausgeführt, ist ein mögliches weiteres Abbruchkriterium die Schrittweitenlänge, wenn diese kleiner wird als eine untere Grenze $\varepsilon >0$ mit der Bedingung $\alpha ^{(j)}<\varepsilon$ .

Verbesserungsschritte als Abbruchbedingung

Ferner kann das Gradientenabstiegsverfahren abgebrochen werden, wenn die Verbesserung der Optimierung von $f$ in den Interationsschritten kleiner als eine untere Grenze wird.

Bedeutung von Abbruchkriterien

Durch solche Abbruchkriterien wird algorithmisch gewährleistet, dass das Gradientenabstiegsverfahren nicht in einer Endlosschleife der Iterationen landet.

Aufgabe

Erläutern Sie, wie im Kontext von künstlichen neuronalen Netzen das Gradientenabstiegsverfahren für die Fehlerminimierung beim Maschinellen Lernen eingesetzt werden kann (Backpropagation)?
Überprüfen Sie, ob und wie man mehrdimensionalen linearen Regression das Gradientenabstiegsverfahren einsetzen kann (siehe Gradient - lineares Funktional)!

Videos

Höhenlinien, Gradient, Vektorfeld, Vektoranalysis, ... Youtube-Video (21.07.2015) von Daniel Jung
Gradient und Totales Differential Youtube-Video (21.07.2015) von Daniel Jung

Literatur

↑ „Gradientenverfahren“. In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 24. September 2016, 13:24 UTC. URL: https://de.wikipedia.org/w/index.php?title=Gradientenverfahren&oldid=158180650 (Abgerufen: 21. November 2017, 11:49 UTC)
↑ ^a ^b Gradientenabstieg mit Tabellenkalkulation, Jörg Rapp, Engelbert Niehaus (2018) GitHub Repository https://github.com/niebert/GradientDescent - ZIP: https://github.com/niebert/GradientDescent/archive/master.zip (letzter Zugriff 2019/04/28)

Siehe auch

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Numerik' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Gradientenabstiegsverfahren
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

[1] „Gradientenverfahren“. In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 24. September 2016, 13:24 UTC. URL: https://de.wikipedia.org/w/index.php?title=Gradientenverfahren&oldid=158180650 (Abgerufen: 21. November 2017, 11:49 UTC)

[githubgradient-2] Gradientenabstieg mit Tabellenkalkulation, Jörg Rapp, Engelbert Niehaus (2018) GitHub Repository https://github.com/niebert/GradientDescent - ZIP: https://github.com/niebert/GradientDescent/archive/master.zip (letzter Zugriff 2019/04/28)

[1]

[2]