Breitensuche

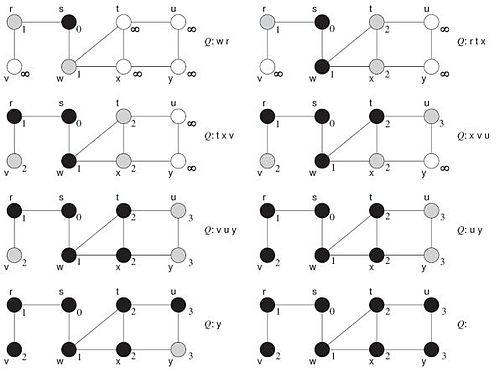
Auf dieser Seite behandeln wir die Breitensuche. Wir fragen uns wie man die Knoten eines Graphen effizient aufzählt. Die Lösung ist der Breitendurchlauf ( Breadth-First-Search, BFS). Dabei werden die Knoten eines Graphen nach der Entfernung vom Zielknoten aufgezählt. Eine andere Methode ist der Tiefendurchlauf, zu dem kommen wir aber später. Bei dem Breitendurchlauf für ungerichtete Graphen gibt es eine Warteschlange als Zwischenspeicher. Farbmarkierungen beschreiben den Status der Knoten. Weiß bedeutet er ist unbearbeitet, grau bedeutet er ist in Bearbeitung und schwarz bedeutet, dass er abgearbeitet ist. Pro Knoten wird die Entfernung zum Startknoten berechnet. Bei der Initialisierung wird der Startknoten in eine Warteschlange eingefügt, die Farbe auf grau gesetzt und die Entfernung mit 0 berechnet. Die anderen Knoten haben eine unendliche Entfernung und sind weiß markiert.

Beim Breitendurchlauf wird der aktuelle Knoten k aus der Warteschlange genommen und schwarz gefärbt. Alle von k aus erreichbaren weißen Knoten werden grau gefärbt, die Entfernung ist der Entfernungswert von k+1 und sie werden in der Warteschlange aufgenommen.

Algorithmus

Ergänzung zum Graph-Interface:

public interface Graph{
   public int addNode();
   public boolean addEdge(int orig, int dest);
   public Collection<Integer> getChildren(int node);!
}

Breitendurchlauf als Iterator:

public class BfsIterator implements Iterator<Integer>{
   private Graph g; 
   private Queue<Integer> q;
   private Set<Integer> visited;

   public BfsIterator(Graph g, int s){
      this.g = g;
      this.q = new LinkedList<Integer>();
      q.add(s);
      this.visited = new HashSet<Integer>();
   }

   public boolean hasNext() { return !this.q.isEmpty(); }

   public Integer next() {
      Integer n = this.q.poll();
      for(Integer m: this.g.getChildren(n))
           if(!this.visited.contains(m) && !this.q.contains(m))
             this.q.add(m);
      this.visited.add(n);
      return n;
   }
}

Ausgabe aller Knoten:

//Sei g ein Graph
Iterator<Integer> it = new BfsIterator(g,1);
while(it.hasNext())
   System.out.println(it.next());

Analyse

Theorem der Terminierung

Die Breitensuche terminiert nach endlicher Zeit

Theorem der Korrektheit

Ist G zusammenhängend, so werden alle Knoten von G genau einmal besucht.

Theorem der Laufzeit

Ist G=(V,E) zusammenhängend und ist die Laufzeit von getChildren linear in der Anzahl der Kinder, so hat die Breitensuche eine Laufzeit von O(|V| + |E|).