Backtracking[Bearbeiten]

Auf dieser Seite wird das Backtracking behandelt.

Die Idee des Backtracking ist das Versuchs-und-Irrtum-Prinzip (trial and error). Versuche, die erreichte Teillösung schrittweise zu einer Gesamtlösung auszubauen. Falls die Teillösung nicht zu einer Lösung führen kann, dann nimm den letzten Schritt bzw. die letzten Schritte zurück und probiere stattdessen alternative Wege.Alle in Frage kommenden Lösungswege werden ausprobiert. Vorhandene Lösung wird entweder gefunden (unter Umständen nach sehr langer Laufzeit) oder es existiert definitiv keine Lösung. Backtracking (“Zurückverfolgen“) ist eine allgemeine systematische Suchtechnik. KF ist die Menge von Konfigurationen. $K_{0}$ ist die Anfangskonfiguration. Für jede Konfiguration $K_{i}$ gibt es eine direkte Erweiterung $K_{i,1},...,K_{i,n_{i}}$ . Außerdem ist für jede Konfiguration entscheidbar, ob sie eine Lösung ist. Aufgerufen wird Backtracking mit $BACKTRACK(K_{0})$ .

Labyrinth Suche[Bearbeiten]

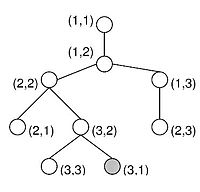
Backtracking Muster[Bearbeiten]

procedure BACKTRACK (K: Konfiguration)
begin
	…
	if [ K ist Lösung ]
	then [ gib K aus ]
	else
		for each [ jede direkte Erweiterung K0 von K ]
			do
				BACKTRACK (K0)
			od
	fi
end

Einsatzfelder[Bearbeiten]

Zu den typischen Einsatzfeldern von Backtracking gehören zum Beispiel einige Spielprogramme (Schach, Dame, Labyrinthsuche,…). Aber auch die Erfüllbarkeit von logischen Aussagen wie logische Programmiersprachen, Optimierung von Gattern oder Model checking (Theorembeweiser). Ein weiteres Einsatzfeld sind Planungsprobleme und Konfigurationen wie logistische Fragestellungen (Traveling Salesman, der kürzeste Wege, die optimale Verteilung, das Färben von Landkarten oder auch nichtdeterministisch-lösbare Probleme.

Beispiel Acht Damen Problem[Bearbeiten]

Gesucht sind alle Konfigurationen von 8 Damen auf einem 8 x 8-Schachbrett, so dass keine Dame eine andere bedroht. Gesucht ist nun ein geeignetes KF. Für jede Lösungskonfigurationen L mit gelten $L\subseteq KF$ . Für jedes $k\in KF$ ist leicht entscheidbar, ob $k\in L$ . Die Konfigurationen lassen sich schrittweise erweitern und wir erhalten eine hierarchische Struktur. Es sollte auch beachtet werden, dass KF nicht zu groß sein sollte.

$L_{1}$ : Es sind 8 Damen auf dem Brett

$L_{2}$ : Keine zwei Damen bedrohen sich.

KF wird so gewählt, dass die Konfiguration mit je einer Dame in den ersten n Zeilen, $1\leq n\leq 8$ , so dass diese sich nicht bedrohen.

Diese Konfiguration ist nun nicht mehr erweiterbar. Jedes Feld in Zeile 7 ist bereits bedroht.

procedure PLATZIERE (i:[1..8]);
begin
   var h: [1..8];
   for h:=1 to 8 do
      if [Feld in Zeile i, Spalte h nicht bedroht]
      then
         [Setze Dame auf dieses Feld (i,h)];
         if [Brett voll] /* i=8*/
         then [Gib Konfiguration aus ]
         else PLATZIERE (i+1)
         fi
      fi
   od
end

Die Array Repräsentation ist [4,1,3,5,0,0,0,0]. Die Diagonalen sind belegt wenn:

i+h = i+h

i-h = i-h

(i = Spalte, h = Zeile)

Die Zeilen snd belegt, wenn die Position im Array besetzt ist und die Spalten sind belegt, wenn die Nummer im Array existiert.

Der initiale Aufruf geschieht mir Platziere(1). Es gibt insgesamt 92 Lösungen. Die Konfigurationen ist etwa als zweidimensionales boolesches Array oder als eindimensionales Array mit einer Damenposition pro Zeile realisierbar. Redundante Informationen über bedrohte Spalten und Diagonalen bieten Optimierungspotential.

Algorithmus in Java[Bearbeiten]

Der Code zu dem Problem im allgemeinen Fall sieht in Java wie folgt aus.

public boolean isValid(int[] board, int current, int place){
   for(int i = 0; i < current-1; i++){
      if(board[i] == place) return false;
      if(place+current == board[i] + (i+1)) return false;
      if(place-current == board[i] - (i+1)) return false;
   }
   return true;
}

public int[] placeQueen(int[] board, int current){
   int[] tmp;
   for(int i=0; i< board.length; i++){
      if(isValid(board, current, i)){
         board[current-1] = i;
         if(current == board.length) return board;
         else{
            tmp = placeQueen(board, current+1);
            if(tmp != null) return tmp;
         }
      }
   }
   return null;
}

Aufgerufen wird der Code durch:

int[] result = placeQueen(new int[8], 1);

Analyse[Bearbeiten]

Theorem

Der Algorithmus $placeQueen$ terminiert nach endlich vielen Schritten, wenn die Anzahl der Felder positiv ist.

Beweis

Die Methode $isValid$ terminiert offensichtlich immer.

In $placeQueen$ wird rekursiv $placeQueen$ stets um einen erhöhten Parameter $current$ aufgerufen. Die for-Schleife hat auch stets eine konstante Zahl an Durchgängen.

Theorem

Für ein Feld der Größe n x n hat der Algorithmus $placeQueen$ eine Laufzeit von $O(n^{n})$ .

Beweis

Im schlimmsten Fall werden alle Konfigurationen betrachtet:

n Positionen für eine einzelne Dame
n Damen sind zu plazieren

Die tatsächliche Laufzeit ist weitaus geringer, da viele Konfigurationen schon früh als nicht-erweiterbar erkannt werden. Dennoch ist die Laufzeit im schlimmsten Fall exponentiell $O(2^{n})$ .

Theorem

Der Algorithmus $placeQueen$ löst das n-Damenproblem.