Vorgehensweise

Zuerst muss man wissen wie man einen Binärbaum in einen Heap transformiert. Dann wie man einen Binärbaum in einen Heap transformiert nachdem er verändert wurde und wie kann man die Idee des HeapSorts nutzen um ein Array zu sortieren?

siftUp

SiftUp bedeutet wörtlich "hochsieben". Wenn ein Knoten nicht die Heap-Eigenschaft hat, dann kann man ihm diese verleihen, indem man seinen Wert mit dem Wert des größeren Kindes tauscht. Das nennt man dann sifting up. Das Kind kann dadurch allerdings die Heap Eigenschaft verlieren.

Konstruktion eines Heaps

Ein Baum, der nur aus einem Knoten besteht, ist ein Heap. Wir konstruieren einen Heap durch inkrementelles Hinzufügen von Knoten. Von rechtes wird der Knoten eingefügt, der am tiefsten und am weitesten rechts steht. Wenn die tiefste Ebene voll ist, dann wird eine neue Ebene begonnen.

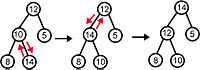
Beispiel:

Jedes mal wenn wir einen Knoten hinzufügen, kann die Heap-Eigenschaft des Eltern-Knoten zerstört werden, dann wird ein Sift-up durchgeführt. Bei jedem Sift-up wächst der Wert des oben liegenden Knotens und das kann die Heap-Eigenschaft seines Elterknotens zerstören. Sift-up wird wiederholt im Baum nach oben durchgeführt bis entweder ein Knoten erreicht wird, dessen Werte nicht ausgetauscht werden müssen, weil der Elterknoten immer noch größer ist als beide Kinder, oder wenn man den Wurzelknoten erreicht.

Im ersten Schritt ist der Knoten mit dem Wert 8 nicht betroffen, da sein Elternknoten größer wird und nicht kleiner. Im zweiten Schritt ist der Knoten mit dem Wert 5 nicht betroffen, da sein Elternknoten größer wird und nicht kleiner. Der Knoten mit dem Wert 8 ist immer noch nicht betroffen. Obwohl sein Elternknoten kleiner wird, ist es immer noch größer als am Anfang.

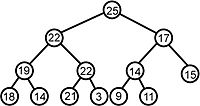
Beispielheap

Heap bedeutet nicht, dass der Binärbaum sortiert ist. Den Binärbaum in einen Heap zu verwandeln, ändert nicht die Gestalt des Baumes. Dieser Binärbaum ist balanciert und linksbündig, weil er am Anfang balanciert und linksbündig war.

Bei der Entfernung des Wurzelknotens muss der Binärbbaum so repariert werden, dass er erneut balanciert und linksbündig ist. Das geschieht dadurch, dass der am weitesten rechts gelegene Blattknoten in der Tiefe entfernt wird und er als Wurzelknoten benutzt wird.

Nun ist der Baum balaciert und linksbündig, aber er hat seine Heap Eigenschaften verloren. Daher müssen wir siftUp() auf dem Wurzelknoten ausführen. Anschießend hat genau ein Kind die Heap-Eigenschaft verloren.

Nun fehlt dem linken Kind des Wurzelknotens die Heap Eigenschaft ( der mit dem Wert 11). Wir führen wieder ein siftUp() dieses Knotens durch. Wiederrum verliert genau ein Kind die Heap Eigenschaft.

Nun fehlt dem rechten Kind des linken Kindes des Wurzelknotens die Heap-Eigenschaft (der mit dem Wert 11). Wir führen wieder ein siftUp() dieses Knotens durch. Jetzt könnte ein Kind die Heap-Eigenschaft verloren haben – das ist aber nicht der Fall, da es ein Blattknoten ist.

Der Baum ist nun wieder ein Heap, da jeder Knoten die Heap Eigenschaft besitzt. Der größte Werte ist wieder im Wurzelknoten. Wir können den Prozess wiederholen, bis der Baum leer ist. Dies liefert eine Folge der Werte, zuerst die Größten, dann die Kleinsten.

Sortieren

Was haben Heaps mit Sortieren zu tun? Hierbei handelt es sich um den interessanten Teil. Da der Binärbaum balanciert und linksbündig ist, kann er leicht als Array repräsentiert werden. Alle Operationen auf Binärbäumen können als Operationen auf Arrays formuliert werden Das Sortieren läuft wie folgt ab:

Mache das Array zum Heap;
while das Array nicht leer ist {
   entferne und ersetze die Wurzel;
   reheap den neuen Wurzelknoten; 
}

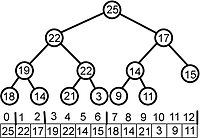
Abbildung in Array

Das Kind von Index i ist bei Index $2\cdot i+1$ . Das rechte Kind von Index i ist bei Index $2\cdot i+2$ . Beispielsweise sind die Kinder von Knoten 3 (19) die Knoten 7 (18) und 8 (14).

Entfernen und Ersetzen des Wurzelknotens

Der Wurzelknoten ist das erste Element im Array. Der Knoten in der tiefsten Ebene, der am weitesten rechts gelegen ist, ist das letzte Element. Nun werden die beiden Knoten getauscht und tue so als würde das letzte Element im Array nicht mehr existieren – der neue letzte Indexeintrag ist nun 11 (9).

Reheap und Wiederhole

Nun wird der Wurzelknoten zum Heap Knoten gemacht (Index o, enthält die 11) und der Wurzelknoten wird entfernt und wieder ersetzt. Jetzt hat sich aber der höchste Indexwert geändert. Die Prozedur wird nun so lange wiederholt, bis der höchste Indexwert auf 0 liegt und das Array somit sortiert ist.

Pseudo Code

Mache das Array zum Heap;
While das Array ist nicht leer { 
   Entferne und ersetze den Wurzelknoten;
   reheap den neuen Wurzelknoten; 
}

HeapSort in Java

void heapSort(int[] f){
   makeHeap(f);  // Erstelle Heap aus Array
   for(int i = f.length - 1; i > 0; i--){
      swap(f,0,i); //Entferne Wurzel
      reHeap(f,i-1); //Repariere Heap bis Index i-1
   }
}

void swap(int[] f, int x, int y){
   int tmp = f[x];
   f[x] = f[y];
   f[y] = tmp;
}

void makeHeap(int[] f){
   for(int i = 1; i < f.length; i++)
      siftUp(f,i); //Füge Elemente dem Heap hinzu und repariere Heap (bottom-up)
}

void siftUp(int[] f, int idx){
   if(idx == 0) //Rekursionsende bei Wurzel
      return;
   int parent=(int)Math.floor((new Double(idx)-1)/2);
   if(f[parent] < f[idx]){ //Vergleiche Wert des Knotens mit Elternknoten; tausche bei Bedarf und fahre beim Elternknoten fort
      swap(f,idx, parent);
      siftUp(f,parent);
  }
}

void reHeap(int[] f, int end){
   int current = 0;
   while(current < end){ //Repariere Heap top-down
      int childLeft = 2*current + 1;
      int childRight = 2*current + 2;
      if(childLeft > end) //falls current Blatt ist sind wir fertig
         return;
      if(childRight <= end){
         if(f[current] >= f[childLeft] && f[current] >= f[childRight])
            //Heap-Eigenschaft erfüllt, nichts mehr zu tun
            return;
         else if(f[childLeft] > f[childRight]){
            swap(f,current,childLeft);
            current = childLeft;
         }else{
            //Vergleiche mit Werten der Kinder, tausche ggfs. und fahre top-down fort
            swap(f,current,childRight);
            current = childRight;
         }
      }else if(f[current] >= f[childLeft])
         //Heap-Eigenschaft erfüllt, nichts mehr zu tun
         return;
      else{
         //Vergleiche mit Werten der Kinder, tausche ggfs. und fahre top-down fort
         swap(f,current,childLeft);
         current = childLeft;
      }
   }
}

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.6.1 zu finden.