Topologisches Sortieren

Auf dieser Seite wird das topologische Sortieren behandelt. Wir fragen uns, wie Knoten unter Berücksichtigung von Abhängigkeiten aufgezählt werden können bei gegebenem azyklischem gerichteten Graph. Zur Anwendung kommt diese Sortierung bei Scheduling bei kausalen und zeitlichen Abhängigkeiten, zum Beispiel bei der Netzplantechnik. Mathematisch liegt hier eine Konstruktion einer totalen Ordnung aus einer Halbordnung vor.

Beispiel

Die sorgfältige Mutter legt ihrem Kind morgens die Kleidungsstücke so auf einen Stapel, dass das Kind nur die Kleidungsstücke vom Stapel nehmen und anziehen muss und dann richtig gekleidet ist. Hierfür legt sie die Reihenfolgebedingungen fest:

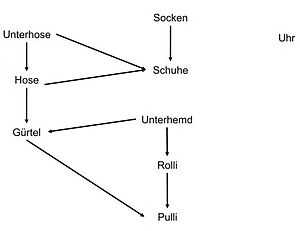
Unterhose vor Hose

Hose vor Gürtel

Unterhemd vor Gürtel

Gürtel vor Pulli

Unterhemd vor Rolli

Rolli vor Pulli

Socken vor Schuhen

Hose vor Schuhen

Uhr: egal

DFS erstellt die topologische Ordnung on the fly. Das Sortieren nach f-Wert (invers) ergibt eine korrekte Reihenfolge. Statt der expliziten Sortierung nach f werden beim Setzen des f-Wertes die Knoten vorne in eine verkettete Liste eingehängt.

18 Socken

16 Unterhose

15 Hose

14 Schuhe

10 Uhr

8 Unterhemd

7 Gürtel

5 Rolli

4 Pulli

Alternativer Durchlauf: