Kurs:Algorithmen und Datenstrukturen (hsrw)/Vorlesung/Berechnung kürzester Weg Dijkstra

Dijkstra Algorithmus[Bearbeiten]

Auf dieser Seite wird der Dijkstra Algorithmus behandelt. Der Dijkstra Algorithmus wird zur Berechnung des kürzesten Weges benutzt (SSSP). Der Algorithmus stammt von 1959. Es erfolgt eine iterative Erweiterung einer Menge von günstig erreichbaren Knoten. Der Greedy Algorithmus hat eine ähnliche Breitensuche ist aber nur für nichtnegative Gewichte. Er berechnet iterativ verfeinert die Distanzwerte d(v,w) und es gibt eine Prioritätswarteschlange zum Herauslesen des jeweils minimalen Elements.

Priority Queues[Bearbeiten]

Eine Priority‐Queue P ist eine dynamische Datenstruktur, die (mindestens) die folgenden Operationen unterstützt:

P.add(Element): Element hinzufügen
P.poll(): Minimalste Element zurückgeben
P.contains(Element): Enthält P das Element?

Die Ordnung zur Sortierung muss dabei vorab deﬁniert sein.

Ein Heap kann beispielsweise zur Implementierung einer Priority‐Queue benutzt werden (add‐Operation ist dann O(log n), poll‐Operation O(log n), und contains‐Operation ist O(n)). Benutzt man zusätzlich zum Heap noch einen binären Suchbaum auf denselben Element so ist auch contains in O(log n) realisierbar.

Priority Queue in Java[Bearbeiten]

class DijkstraComparator implements Comparator<Integer>{
   Map<Integer,Integer> d = new HashMap<Integer,Integer>();

   public DijComparator(Map<Integer,Integer> d){
      this.d = d;
   }

   public int compare(Integer o1, Integer o2) {
      return d.get(o1).compareTo(d.get(o2));
   }
}

Ist d eine Map “Knoten”‐>”Aktueller Distanzwert von s aus”, so ist PriorityQueue<Integer> queue = new PriorityQueue<Integer>(g.getNumberOfNodes(),new DijkstraComparator(d)); eine Priority‐Queue, die bei iterativen Aufruf queue.poll() immer das Element mit dem minimalsten d‐Wert zurückliefert.

Idee[Bearbeiten]

Initialisiere alle Distanzwerte von s zu v mit ∞ (und von s zu s mit 0)
Initialisiere eine Priority‐Queue Q mit allen v
Extrahiere das minimale Element $w_{min}$ aus Q
Aktualisiere alle Distanzwerte der Nachfolger von $w_{min}$ in Q:

Ist es günstiger über $w_{min}$ zu einem Knoten w zu kommen?
Falls ja setzte d(s,w)=d(s, $w_{min}$ )+y( $w_{min}$ ,w)

5. Wiederhole bei 3 solange Q noch Elemente hat

Algorithmus in Java[Bearbeiten]

Map<Integer,Integer> dijkstra(Graph g, int s){
   Map<Integer,Integer> d = new HashMap<Integer, Integer>();
   PriorityQueue<Integer> queue = //Initialisiere Priority-Queue entsprechend
   for(Integer n: g){
      if(!n.equals(s)){
         d.put(n, Integer.MAX_VALUE);
         queue.add(n);
      }
   }
   d.put(s, 0);
   queue.add(s);

   while(!queue.isEmpty()){
      Integer u = queue.poll();
      for(Integer v: g.getChildren(u)){
         if(queue.contains(v)){
            if(d.get(u) + g.getWeight(u,v) < d.get(v){
               d.put(v, d.get(u) + g.getWeight(u,v));
            }
         }
      }
   }
   return d;
}

Algorithmus[Bearbeiten]

algorithm Dijkstra (G,s)

Eingabe: Graph G mit Startknoten s

for each Knoten u

\in

V[G] -s do // Initialisierung

D[u] :=

\infty

od;

D[s]:= O; PriorityQueue Q := V;

while not isEmpty (Q) do

U := extractMinimal (Q);

for each v

\in

ZielknotenAusgehenderKanten (u)

\cap

Q do

if D[u] +

\gamma

((u,v)) < D[v] then // Entfernung über u nach v kleiner als aktuelle Entfernung D[v]

D[v] := D[u] +

\gamma

((u,v));

adjustiere Q an neuen Wert D[v]

fi

od

Initialisierung[Bearbeiten]

$D[s]+\gamma (s,u)<D[u]?$

$0+10<\infty$

$\Rightarrow D[u]=10$

$D[s]+\gamma (s,x)<D[x]?$

$0+5<\infty$

$\Rightarrow D[x]=5$

$Q=\langle (s:0),(u:\infty ),(v:\infty ),(y:\infty )\rangle$

$D[x]+\gamma (x,u)<D[u]?$

$5+3<10$

$\Rightarrow D[u]=8$

$D[y]analog$

$Q=\langle (x:5),(u:10),(v:\infty ),(y:\infty )\rangle$

$Q=\langle (y:7),(u:8),(v:\infty )\rangle$

$Q=\langle (u:8),(v:13)\rangle$

$Q=\langle (v:9)\rangle$

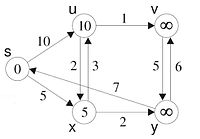
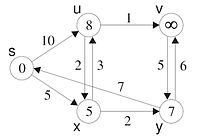
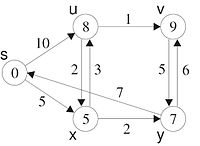
Der Iterationsstart ist korrekt für die Tiefe 0. Wir nehmen an, dass der vorherige Iterationsschritt korrekt war ( Induktionsbeweis). Der Ein Iterationsschritt ist jeweils die günstigste Verbindung zu einem noch nicht bearbeiteten Knoten hinzunehmen. Da die bisher bearbeiteten Knoten den korrekten Distanzwert haben, ist der neue Distanzwert durch den „günstigsten“ aus dem bisher bearbeiteten Teilgraphen um genau eine Kante hinausgehenden Pfad bestimmt. Jeder Pfad zum Zielknoten dieses Pfades, der um mehr als eine Kante aus dem bearbeiteten Bereich hinausgeht, ist teurer als die gewählte, da Kosten mit zusätzlich hinzu genommenen Kanten nicht sinken können.

Analyse[Bearbeiten]

Terminierungstheorem[Bearbeiten]

Der Algorithmus von Dijkstra terminiert für eine endliche Eingabe nach endlicher Zeit.

Beweis[Bearbeiten]

In jedem Schritt der while‐Schleife wird ein Element aus queue entfernt und die Schleife endet sobald queue leer ist. Jeder Knoten hat nur endliche viele Kinder, deswegen ist auch die Laufzeit der inneren for‐Schleife endlich.

Korrektheitstheorem[Bearbeiten]

Sind alle Kantengewichte nicht‐negativ, so enthält d am Ende die Distanzwerte von s zu allen anderen Knoten.

Beweis[Bearbeiten]

Beachte, dass sobald ein Knoten v aus queue entfernt wird, der Wert für v in d nicht mehr geändert wird.

Zeige nun, dass gilt: Wird v aus queue entfernt, so enthält d den Distanzwert von s nach v. Zeige dies durch Induktion nach i=„Anzahl bisher aus queue entfernter Knoten“:

i=0: Am Anfang hat queue nur für s einen endlichen Wert gespeichert, alle anderen Werte sind ∞. Der Knoten s wird auch stets zuerst entfernt und der Distanzwert ist 0. Dies ist auch korrekt, da s zu sich selbst Distanz 0 hat und alle anderen Knoten keine geringere Distanz von s aus haben können (da alle Kanten nicht‐negative Gewichte haben).
i → i+1: Sei v der (i+1)te Knoten, der aus queue entfernt wird.
- Da die bisher bearbeiteten Knoten den korrekten Distanzwert haben, ist der neue Distanzwert durch den „günstigsten“ aus dem bisher bearbeiteten Teilgraphen um genau eine Kante hinausgehenden Pfad bestimmt.
- Jeder Pfad zum Zielknoten dieses Pfades, der um mehr als eine Kante aus dem bearbeiteten Bereich hinausgeht, ist teurer als die gewählte, da Kosten mit zusätzlich hinzugenommenen Kanten nicht sinken können.

Laufzeittheorem[Bearbeiten]

Sei G=(V,E,g) ein gerichteter Graph. Der Laufzeitaufwand von Dijkstras Algorithmus für einen beliebigen Knoten s in G ist O((|E| + |V|) log |V|).

Beweis[Bearbeiten]

Beachte: Wird für die Priority‐Queue beispielsweise ein Heap verwendet, so hat die Operation poll() einen Aufwand von O(log k) (mit k=„Anzahl Elemente in Queue“). Sei |V|=n und |E|=m. Insgesamt: O(n log n) + O(n) + n* O(log n) + m *O(log n) = O((m + n) log n) Durch Benutzung sog. Fibonacci‐Heaps (anstatt normaler Heaps) kann die Laufzeit von O((m + n) log n) verbessert werden zu O(m + n log n)

Nachteile[Bearbeiten]

Der kürzeste Weg wird immer gefunden, aber es werden viele unnötige und sinnlose Wege gegangen. Bei negativen Kanten resultieren auch falsche Ergebnisse.