Kurs:Experimentalphysik 1

Aus Wikiversity

Wechseln zu: Navigation, Suche

Dieser Kurs gehört zum Fachbereich Physik.

Inhaltsverzeichnis

[Bearbeiten] Einleitung: Aufbau und Ziel des Kurses

Dieser Kurs beginnt zum Sommersemester 2007 (23. April 2007) unter der Voraussetzung, dass sich eine angemessene Zahl von interessierten Teilnehmern gefunden hat. Sehr wünschenswert wären dabei etwa zehn Teilnehmer, die sich hier eingetragen, bei Wikiversity angemeldet, eine Benutzerseite mit kurzer Motivation und Darstellung ihrer persönlichen Voraussetzungen erstellt haben und schließlich auch noch über die Wikiversity-eMail-Funktion erreichbar sind.

Derzeit sind genau zehn Teilnehmer eingetragen, von denen alle diese wünschenswerten Voraussetzungen erfüllen.


[Bearbeiten] Beschreibung und Vorkenntnisse

Dieser Kurs soll die bundesweit größtenteils einheitlichen Inhalte einer Anfängervorlesung in Experimentalphysik widergeben, die sich hauptsächlich an Studierende der Physik (B.Sc., Diplom und Lehramt) im ersten Semester richtet. Neben der klassischen Mechanik des Massenpunktes, deren Grundlage bereits aus der Sekundarstufe des Gymnasiums bekannt sind, werden dabei die Mechanik starrer Körper, Relativitätstheorie sowie Elemente der Kontinuumsmechanik behandelt.

Voraussetzungen für diesen Kurs sind gründliche Kenntnisse der Differential- und Integralrechnung einer reellen Veränderlichen sowie erste Kenntnisse der angewandten Differential- und Integralrechnung mehrerer Veränderlicher. Dies sind vor allem die Kenntnis von impliziten Funktionen, partiellen Ableitungen, Mehrfachintegralen sowie der grundlegenden Bedeutung von Differentialgleichungen.


[Bearbeiten] Zielpublikum und Inhalt

Der Kurs richtet sich vornehmlich an zukünftige Studenten der Physik, die bereits das Abitur erlangt haben oder demnächst erlangt haben werden sowie an alle Interessierten, die vergleichbare Voraussetzungen erfüllen. Gründliche Kenntnisse der Schulmathematik sind unumgänglich und werden in diesem Kurs nicht besonders ausführlich wiederholt. Methoden der höheren Mathematik, insbesondere der Analysis mehrerer Variablen werden an gegebener Stelle kurz und heuristisch eingeführt. Grundsätzlich sollte dies allerdings die Aufgabe eines noch einzurichtenden Kurses über die Rechenmethoden der Physik sein.


[Bearbeiten] Übungen und Kursablauf

Nach Kursbeginn werden zu allen Abschnitten Übungen angeboten, die zur Vertiefung und Anwendung des Stoffes dienen sollen und deren Bearbeitung unbedingt empfohlen wird. Das wöchentliche Zeitpensum für die vollständige Bearbeitung der Übungen soll vier Stunden nicht überschreiten. Diese Zeitspanne variiert natürlich individuell und soll hier hauptsächlich verdeutlichen, welchen Umfang das Angebot an Übungen haben wird.

Ausserdem werden Beispiele angeboten, die auch Lösungen beinhalten, was eine Hilfestellung zur Lösung der Aufgaben sein soll.

Es wird eine intensive Diskussion der Aufgaben mit dem Betreuer und für bestimmte Aufgaben auch unter den Kursteilnehmern angestrebt. Diese soll auf den Diskussionsseiten der Benutzer stattfinden, die an diesem Kurs teilnehmen.

[Bearbeiten] Einführung

Bevor es auch gleich ins eingemachte geht, möchte ich an dieser Stelle folgende Dinge klarstellen. Die Wikipedia-Artikel sind meistens bereits auf einem recht hohen und damit für die Hochschule durchaus akzeptablem Niveau angesiedelt. Das bedeutet, dass sie sich einwandfrei zur direkten Verwendung in einem Kurs wie diesem hier eignen. Natürlich sind sie keineswegs fehlerfrei, was aber nicht so viel ausmacht, denn ein normales Vorlesungsskriptum ist dies schliesslich auch nicht. Die meisten Artikel enthalten allerdings nur wenige Fehler. Ziel dieses Kurses kann unter anderem auch sein, dass solche Fehler gefunden, diskutiert und auch behoben werden können. Ich werde in grossen Teilen des Kurses nur eine Leseanleitung für die notwendigen Wikipedia-Artikel geben. Das bedeutet also, dass alle Artikel, die hier verlinkt sind gelesen werden sollten. Bzw. die angegebenen Stellen und Abschnitte. Die Artikel werden evtl. kommentiert. Falls ein Artikel nicht zu den obligatorischen Lesestücken gehören sollte, wird dies an dieser Stelle extra erwähnt. Alle obligatorischen Artikel/Abschnitte aus Wikipedia werden hier gesammelt. Neben den Lesehinweisen und zusätzlichen Anmerkungen sollen auch erklärende bzw. vertiefende Skizzen hier eingefügt werden.

So, jetzt geht's aber richtig los:

Der (erste) Artikel Physik behandelt im ersten Abschnitt Methodik der Physik das Problem der Modellbildung und das Verhältnis von Theorie und Experiment sehr gut.

Zusammenfassend sieht das Konzept der Physik etwa so aus:

Wichtig ist noch zu erwähnen, dass jede physikalische Theorie nur im Rahmen ihres Gültigkeitsbereiches betrachtet werden darf. Vor allem ist zunächst wichtig die Unterscheidung zwischen makroskopischer und mikroskopischer Physik. Wie der Name schon sagt, bewegt man sich noch im (zunächst) sicheren Bereich der makroskopischen Physik, solange man Körper behandelt, die so gross sind, dass noch kein Mikroskop zur Betrachtung benötigt wird. (Tatsächlich gilt die makroskopische Physik auch noch ausgezeichnet für um einiges kleinere Dinge, doch dazu später mehr.)

Um die Natur zu beschreiben, benötigen wir die Mathematik. Damit einhergehend brauchen wir Massysteme für physikalische Grössen. Diese werden an den Naturkonstanten festgemacht. Ein Beispiel ist die Feinstrukturkonstante,

(01)\quad \alpha=\frac{e^2}{4\pi\hbar c\epsilon_0}\approx\frac{1}{137}\;.

Die einzelnen vorkommenden Konstanten können auf der genannten Seite nachgesehen werden. Anzumerken ist noch, dass α eine Zahl ohne Einheit ist.

In der theoretischen Physik wird gern mit sogenannten natürlichen Einheiten gerechnet. Das bedeutet, dass man bestimmte Konstanten, wie zum Beispiel die Lichtgeschwindigkeit oder \hbar auf den Wert 1 festsetzt.

Auffallend ist (oder zumindest gibt es tatsächlich Leute, denen das aufgefallen ist!), dass folgendes gilt:

(02)\quad \frac 1\alpha=137{,}...=111\cdot 1{,}23456789\;.

Beginnt man, darüber nachzudenken, welche physikalische Bedeutung dieser Zusammenhang haben könnte, kann man auch schon wieder aufhören darüber nachzudenken. Das Einheitensystem ist vom Menschen gemacht, die Gesetze der Physik aber nicht. Es handelt sich also um einen blossen Zufall, eine Zahlenspielerei. Es steckt kein physikalisches, das bedeutet, kein überprüfbares Modell, keine überprüfbare Theorie dahinter. Man spricht von Numerologie (der Artikel braucht nicht gelesen zu werden).

[Bearbeiten] Basiseinheiten und -größen

Als Europäer haben wir das Glück, bereits von Kind auf an das metrische System gewöhnt zu sein. Daher braucht man an dieser Stelle nicht allzu viele Worte verlieren. Der Abschnitt Basiseinheiten im SI-System gibt mehr Auskunft zu den in diesem Kurs verwendeten und auch gesetzlich vorgeschriebenen Einheiten. In diesem Kurs werden wir lediglich die drei Einheiten für Länge, Masse und Zeit verwenden, sowie von diesen dreien abgeleitete Einheiten. Daher am besten gleich gut einprägen, dass dies Sekunden, Kilogramm und Meter sind, auf die man die entsprechenden Grössen umrechnen muss. Tut man dies konsequent, so kann man sicher sein, dass man auch jederzeit wieder eine SI-Einheit herausbekommt am Ende seiner Rechnungen. Auf der anderen Seite ist das auch eine gute Kontrollmöglichkeit.

[Bearbeiten] Dezimalvorsätze

Um grosse Zehnerpotenzen zu vermeiden, gibt es die sogenannten Dezimalvorsätze, die man vor eine Einheit setzt anstatt die entsprechende Zehnerpotenz auszuschreiben. Zum Umrechnen schreibt man dann einfach die Zehnerpotenz wieder aus und lässt den Dezimalvorsatz weg. Die im Artikel aufgelisteten Vorsätze Yokto, Zepto sowie Exa, Zetta und Yotta sind eher ungebräuchlich. Man beachte ausserdem: Mehrfache Dezimalvorsätze sind unzulässig! Es gibt also keine Dezikilogramm und dergleichen.

[Bearbeiten] Messung und Messunsicherheit

  • Die korrekte Schreibweise für eine physikalische Grösse ist

Messgrösse = (Messzahl \pm Unsicherheit)\cdot Einheit,

wobei jedoch der Malpunkt meist weggelassen wird.

  • Es gibt keine Messungen ohne Unsicherheiten!
  • Messfehler
  • quantifizieren die Unsicherheit einer Messung
  • erlauben eine Interpretation der Messung (und ihrer Güte)
  • Arten von Messfehlern
  • systematische Fehler
  • Eichung der Messapparatur
  • Durchführung des Messvorgangs
  • Entstehung durch Abänderung des Messaufbaus
  • Führen zu systematisch falschen Messwerten
  • statistische Fehler
  • Ableseungenauigkeiten
  • unkontrollierbare Störungen
  • Zufälligkeit des untersuchten Prozesses
  • sind reduzierbar durch mehrfache Wiederholung der Messung

Beispiele finden sich im Abschnitt Fehlerquellen.

[Bearbeiten] Kurzer Überblick zur Statistik

Ein sehr häufiger und wichtiger Vorgang, um statistische Fehler zu verringern, ist die Mittelwertbildung. Statistische Fehler können bei ausreichend grosser Versuchsanzahl herausgemittelt werden.

Ein Maß dafür, wie stark die einzelnen Werte um ihren Mittelwert verstreut sind, ist die Standardabweichung. Sie gibt gewissermassen die Breite der Verteilung der Werte an. An der Formel fällt auf, dass die Anzahl N der Messwerte unter der Wurzel im Nenner auftaucht. Das bedeutet, dass die Streuung umso kleiner wird, je mehr Messwerte man hat! Das ist aber eine unter Umständen leicht kontrollierbare Grösse. Siehe dazu auch noch den Artikel zum Standardfehler.

An dieser Stelle sollen diese wichtigen Tatsachen aus der Statistik ohne viele Beispiele nur erwähnt. Zu gegebener Zeit werden Beispiele folgen. Eventuell sollte das auch eines der Themen für einen Online-Kurs zum Anfängerpraktikum sein. Denn gerade in den Anfängerpraktika zur Physik werden Kenntnisse zur Auswertung von Messergebnissen hauptsächlich vermittelt. Mit dem nächsten Abschnitt sei daher das Gesamtthema "Auswertung von Messergebnissen" für diesen Kurs abgeschlossen.

[Bearbeiten] Fehlerfortpflanzung

Wie der Name schon andeutet, können sich bei der Messung entstandene Fehler durch Rechenoperationen oder die Anwendung von Funktionen auf den Messwert fortpflanzen und verändern. Betrachten wir dazu die folgende Skizze.

Dabei sei x eine Messgrösse, auf die die Funktion y = f(x) angewandt wird. Der gemessene Mittelwert sei \bar x und der Standardfehler heisse σx. Die Tangente an den Graph von f(x) an der Stelle x hat die Steigung \frac{{\rm d}f}{{\rm d}x}\,\bigg|_{x=\bar x}, wobei die Schreibweise einfach bedeutet, dass die Ableitung an der Stelle x=\bar x betrachtet wird. Auf diese Weise sieht man, dass sich der Fehler σx in den Fehler σy transformiert, wobei gilt

(04)\quad \sigma_y=\frac{{\rm d}f}{{\rm d}x}\,\bigg|_{x=\bar x}\,\cdot\,\sigma_x\;.

Achtung! Wie man auch schon an der Skizze erkennen kann, gilt diese Formel nur in einem lokalen Bereich um den Wert \bar x herum. Sobald die Funktion stärker variiert, stimmt dieser Zusammenhang nicht mehr.

Hat man es allgemeiner mit einer Funktion mehrerer Messgrössen x_1,\,x_2,\,...x_N zu tun, so gilt das Gauss'sche Fehlerfortpflanzungsgesetz:

(05)\quad \sigma_y=\sqrt{\sum_{i=1}^N\left(\frac{\partial f}{\partial x_i}\right)^2\cdot \sigma_{x_i}}\;.

Mehr dazu findet sich im Artikel Fehlerfortpflanzung.

[Bearbeiten] Kinematik eines Massenpunktes

Zunächst beschäftigen wir uns mit dem einfachsten denkbaren physikalischen Vorgang. Es handelt sich dabei um die Bewegung eines Massenpunktes. Die Kinematik ist das Teilgebiet der Physik, die Bewegungen beschreibt. Das bedeutet, daß sie sich noch nicht mit der Ursache dieser Bewegung beschäftigt, sondern lediglich eine Beschreibung liefern will.

Jede Bewegung läßt sich grundsätzlich so zerlegen, daß sie aus den grundlegenden Bewegungsarten Translation (Verschiebung) und Rotation (Drehung) besteht. Es gibt also nur Verschiebungen und Drehungen. Grund genug, sich zu gegebener Zeit mit jeder von beidem ausführlich zu beschäftigen. Rotationen kommen später.

Zur Beschreibung der Bewegung eines Massenpunktes müssen wir seine Position als Vektor angeben können.

Zum Beispiel in kartesischen Koordinaten:

(06)\quad\vec r=\left(\begin{array}{c}x_1\\y_1\\z_1\end{array}\right)\;\;.

Um seine Bewegung zu beschreiben, benötigt man die Koordinaten, also den Ortsvektor auch als Funktion der Zeit:

(07)\quad\vec r(t)=\left(\begin{array}{c}x_1(t)\\y_1(t)\\z_1(t)\end{array}\right)\;\;.

Andere Koordinatensysteme sind

  • Kugelkoordinaten (R,\,\varphi,\,\vartheta\,)\,,
  • Zylinderkoordinaten (R,\,\varphi,\,z\,)\,,

doch mehr dazu ebenfalls später.

Betrachten wir nur eine der Koordinaten, so können wir uns einige Begriffe zunächst am einfachen, eindimensionalen Fall klarmachen. Betrachten wir dazu das folgende Weg-Zeit-Diagramm, bei dem der zurückgelegte Weg x (nach oben) gegen die vergangene Zeit t (nach rechts) aufgetragen ist, also x(t) dargestellt ist.

Die Kurven zeigen von unten nach oben

  • einen ruhenden Massenpunkt,
  • einen gleichförmig-geradlinig bewegten Massenpunkt (d.h. mit konstanter Geschwindigkeit),
  • einen gleichförmig (oder auch gleichmäßig) beschleunigten Massenpunkt.

Die Geschwindigkeit wird in der Schule oft definiert als

(08)\quad v=\frac{\Delta x}{\Delta t}\;\;,

was aber richtiger gesagt die Definition der Durchschnittsgeschwindigkeit ist. Die Geschwindigkeit (genauer Momentangeschwindigkeit) definieren wir als erste Ableitung des Weges nach der Zeit, also

(09)\quad v=\frac{{\rm d}x}{{\rm d}t}=:\dot x\;\;,

wobei der Punkt (hier und von nun an immer) eine Ableitung nach der Zeit bedeutet. Der Wikipedia-Artikel zur Geschwindigkeit wird nicht als Lesestück empfohlen, da er fehlerhaft ist, vor allem in den Teilen, in denen auch die Energie erwähnt wird. Wer ihn trotzdem lesen möchte, sollte dies also mit Vorsicht genießen.

Die Durchschnittsbeschleunigung definieren wir konsequent

(10)\quad a=\frac{\Delta v}{\Delta t}\;\;,

und die Momentanbeschleunigung als

(11)\quad a=\frac{{\rm d}v}{{\rm d}t}=\dot v\;\;.

Daraus folgt

(11)\;\Longrightarrow\;(12)\quad a=\frac{\rm d}{{\rm d}t}\left(\frac{{\rm d}x}{{\rm d}t}\right)=\frac{{\rm d}^2 x}{{\rm d}t^2}=\ddot x\;\;.

Dabei bedeutet ein zweifacher Punkt logischerweise die zweite Ableitung einer Größe nach der Zeit.

Im Rest des Abschnittes wird die Information etwas komprimiert dargestellt, da vieles von der Schule her noch bekannt sein dürfte.

Kommen wir zu den Bewegungsgesetzen für die 1-dimensionale gleichförmig beschleunigte Bewegung. Dabei gilt:

(13)\quad a(t)=a={\rm const.}\;\;.

(14)\quad a(t)=\frac{{\rm d}v}{{\rm d}t}\;\Longrightarrow\;v(t)=\int a(t'){\rm d}t'=\int a{\rm d}t'=a\cdot t+{\rm const.}\;\Longrightarrow

(15)\quad v(t)=a\cdot t+v_0\;\;.

(16)\quad v(t)=\frac{{\rm d}x}{{\rm d}t}\;\Longrightarrow\;x(t)=\int v(t'){\rm d}t'=\int\left(a\cdot t'+v_0\right){\rm d}t'=\frac 12at^2+v_0\cdot t+{\rm const.'}\;\Longrightarrow

(17)\quad x(t)=\frac 12at^2+v_0t + x_0\;\;.

Die Werte a, v0 und x0 sind Startwerte. Bei gleichförmigen Bewegungen mit konstanter Geschwindigkeit folgt mit a\overset{!}{=}0

(18)\quad x(t)=v_0t+x_0\;\;,

(19)\quad v(t)=v_0\;\;,

(20)\quad a=0\;\;.

Zur Wiederholung und Vertiefung wird der Wikipedia-Artikel zur Beschleunigung an dieser Stelle empfohlen.

Bei Bewegungen in einer Ebene bzw. im Raum werden sämtliche vorherigen Betrachtungen analog auf die Komponenten der entsprechenden Vektoren bezogen. Das bedeutet also, daß Ort, Geschwindigkeit und Beschleunigung Vektoren sind:

\vec r(t)\;,\quad \vec v(t)\;,\quad \vec a(t)\;\;.

Entsprechend

(21)\quad \vec v(t)=\frac{{\rm d}\vec r(t)}{{\rm d}t}=\left(\begin{array}{c}\frac{{\rm d}x}{{\rm d}t}\\\frac{{\rm d}y}{{\rm d}t}\\\frac{{\rm d}z}{{\rm d}t} \end{array}\right)=\dot{\vec r}(t)\;\;,

bzw.

(22)\quad \vec a(t)=\dot{\vec v}(t)=\ddot{\vec r}(t)\;\;.

Das Superpositionsprinzip besagt kurz folgendes:

Gleichzeitig verlaufende Bewegungen überlagern sich ungestört und addieren sich geometrisch.

Hat man also wie in obiger Abbildung dargestellt die Bewegung des Wassers eines Flußes und zusätzlich die (Eigen-)Bewegung eines Schiffes, so addieren sich dieses nach dem Prinzip der Vektoraddition (siehe unten).

Es ist dann

(23)\quad \vec v_{\rm Fluss}+\vec v_{\rm Schiff}=\vec v_{\rm Gesamt}\;\;.

An dieser Stelle sei auf die Artikel zu den beiden zuvor genannten grundlegenden Bewegungsarten verwiesen, aus denen alle - auch die superponierten - Bewegungen zusammengesetzt sind: Translation und Rotation. Bei letztgenanntem Artikel ist nur der erste Abschnitt zu lesen.

Das Superpositionsprinzip findet Anwendung beim waagrechten Wurf, den wir im folgenden besprechen werden.

Nach Gleichung (17) und mit Hilfe obiger Skizze gilt in vektorieller Schreibweise in der Wurfebene

(24)\quad \vec r(t)=\frac 12\vec at^2+\vec v_0t+\vec r_0\;\;.

Mit den Startwerten

\vec r_0=\dbinom{0}{h}\;,\quad \vec v_0=\dbinom{v_{x,0}}{0}\;,\quad \vec a=\dbinom{0}{-g}\;\;,

wobei g\approx 10\,{\rm m}/{\rm s}^2 die Erdbeschleunigung ist, gilt dann

(25)\quad \vec r(t)=\frac 12\dbinom{0}{-g}t^2+\dbinom{v_{x,0}}{0}\cdot t+\dbinom{0}{h} =\dbinom{\frac 12\cdot 0\cdot t^2+v_{x,0}\cdot t+0}{-\frac 12gt^2+0\cdot t+h} =\dbinom{v_{x,0}\cdot t}{-\frac 12 gt^2+h}\overset{!}{=}\dbinom{x_e}{0}\;\;.

Hierbei ist \dbinom{x_e}{0} der (noch unbekannte) Auftreffpunkt. Somit ergibt sich für die Flugzeit te

\Longrightarrow\;v_{x,0}\cdot t\overset{!}{=}x_e\quad\mbox{und}\quad -\frac 12gt_e^2+h\overset{!}{=}0\quad (26)

\Longrightarrow\;t_e^2=\frac{2h}{g}\;\Longrightarrow\;t_e=\sqrt{\frac{2h}{g}}\;\;.\quad (27)

Und für die Wurfweite

\Longrightarrow\;x_e=v_{x,0}\cdot\sqrt{\frac{2h}{g}}\;\;.\quad (28)

Fehlt noch die Auftreffgeschwindigkeit, die wir mit Hilfe von Gleichung (15) wie folgt erhalten:

(29)\quad\vec v_e(t_e)=\vec a\cdot t_e+\vec v_0=\dbinom{0}{-g}\cdot t_e+\dbinom{v_{x,0}}{0}\;\Longrightarrow\;\vec v_e(t_e)=\dbinom{v_{x,0}}{-\sqrt{2gh}}\;\;.

Der Absolutbetrag der Auftreffgeschwindigkeit ergibt sich zu

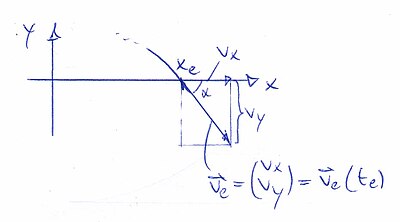
(30)\quad\left|\vec v_e(t_e)\right|=\sqrt{v_{x,0}^2+2gh}\;\;.

Den Auftreffwinkel α erhält man gemäß obiger Skizze wie folgt:

(31)\quad\tan\alpha = \frac{v_y}{v_x}=\frac{-\sqrt{2gh}}{v_{x,0}}\;\;.

Siehe auch den Wikipedia-Artikel zum waagrechten Wurf.

Der schräge Wurf ist im Prinzip nur zweimal ein waagrechter Wurf, wie in obiger Skizze dargestellt. Manchmal spricht man auch vom schiefen Wurf.



Noch offen in diesem Abschnitt: Kreisbewegungen

[Bearbeiten] Newton'sche Mechanik

[Bearbeiten] Newton'sche Axiome

Trägheitsprinzip, Aktionsprinzip, Reaktionsprinzip

[Bearbeiten] Impulserhaltung

Herleitung, Anwendung: Raketenantrieb

[Bearbeiten] Beispiele für Kräfte

Zentripetalkraft, Federkraft, Reibungskräfte, Gravitationskraft

[Bearbeiten] Bewegungsgleichungen mit Kräften

Ortsabhängige Kräfte, Kepler'sche Gesetze, Kegelschnitte

[Bearbeiten] Beschleunigte Bezugssysteme

Relativgeschwindigkeit, Inertialsysteme, Galilei-Transformation

[Bearbeiten] Geradlinig beschleunigte Bezugssysteme

Scheinkräfte

[Bearbeiten] Das Prinzip von d'Alembert

Ruhender Beobachter, mitbewegter Beobachter

[Bearbeiten] Rotierende Bezugssysteme

Zentrifugalkraft, Coriolis-Kraft, Erdrotation, Tief- und Hochdruckgebiete

[Bearbeiten] Arbeit, Energie und Leistung

Definitionen, Einheiten, konservative Kraftfelder, Energiearten, Energieerhaltungssatz, Potentiale

[Bearbeiten] Systeme von Massenpunkten

Schwerpunkt, Schwerpunktsatz, kinetische Energie, reduzierte Masse, Drehimpuls, Drehmoment,

[Bearbeiten] Stöße von zwei Teilchen

Arten von Stößen, Energie- und Impulsübertragung, zentrale und nicht-zentrale Stöße, Streuung

[Bearbeiten] Spezielle Relativitätstheorie

Galilei-Transformation, Michelson-Morley-Experiment

[Bearbeiten] Konsequenzen einer konstanten Lichtgeschwindigkeit

Zeitdilatation, Längenkontraktion

[Bearbeiten] Lorentz-Transformation

Orts- und Zeittransformation, Matrixdarstellung, relativistische Geschwindigkeitsaddition

[Bearbeiten] Gleichzeitigkeit

[Bearbeiten] Minkowski-Diagramme

[Bearbeiten] Paradoxa

Zwillingsparadoxon u.a.

[Bearbeiten] Relativistische Dynamik

Impuls und Energie sowie deren Erhaltung

[Bearbeiten] Anwendungen

Stöße zwischen Teilchen im Beschleuniger

[Bearbeiten] Schwingungen und Wellen

Bedeutung und Auftreten

[Bearbeiten] Harmonische Schwingungen

Allgemeines, Federpendel, Fadenpendel

[Bearbeiten] Gedämpfte Schwingungen

Dämpfung, Grenzfälle, Energiebetrachtung, logarithmisches Dekrement, Energiebetrachtung

[Bearbeiten] Erzwungene Schwingungen

Aufstellen und Lösen der Differentialgleichung, Resonanz, Einschwingvorgang

[Bearbeiten] Überlagerung von Schwingungen

Superpositionsprinzip, Lissajous-Figuren, Schwebung, Fourier-Synthese und -Analyse

[Bearbeiten] Gekoppelte Schwingungen

Eigenfrequenzen und -schwingungen

[Bearbeiten] Wellen

Gekoppelte Oszillatoren, Wellenzahl, Wellenlänge

[Bearbeiten] Harmonische Wellen

Phasengeschwindigkeit, Reflexion, freies oder geschlossenes Ende, stehende Wellen

[Bearbeiten] Wellengleichung (d'Alembert-Gleichung)

Schwingung in Zeit und Ort, d'Alembert-Operator

[Bearbeiten] Wellentypen

Ebene Wellen, Transversal- und Longitudinalwellen, Kugelwellen, elastische Wellen, Schallwellen, Wasserwellen, Kapillarwellen

[Bearbeiten] Dispersion und Gruppengeschwindigkeit

Phasengeschwindigkeit

[Bearbeiten] Interferenz und Kohärenz

Superpositionsprinzip, Überlagerungen

[Bearbeiten] Huygens'sches Prinzip und Beugung

[Bearbeiten] Doppler-Effekt

Relativgeschwindigkeit, Frequenzverschiebung, Mach'scher Kegel

[Bearbeiten] Energiedichte und Intensität

[Bearbeiten] Kinematik und Dynamik starrer Körper

Modell des starren Körpers, Schwerpunkt, Dichte

[Bearbeiten] Drehmoment

Kraft und Drehmoment, Unwucht

Unter dem Drehmoment M einer Kraft F an einem Hebelarm a versteht man das Produkt aus dem Kraftbetrag F und dem Hebelarm a; M=F*a das ist die Definition des Drehmoments, wobei die Richtung der Kraft un die des Hebelarms einen rechten Winkel bilden.

Drehmoment=Kraft*Hebelarm

Die Einheit des Drehmoments ist 1Nm. Sie gibt die Drehwirkung Der Kraft 1N an, die senkrecht zum Hebelarm 1m wirkt (1Nm=100Ncm). Das Drehmoment wird z. B. bei einem Automotor angegeben. Verwechsle nicht mechanische Arbeit mit Drehmoment, beide haben die gleiche Einheit.

Beispielaufgabe:

Ein Fahrradfahrer mit einr Masse von 70Kg fährt ein Rad, dessen Pedale 20cm lang sind. Wie groß ist das maximale Drehmoment, wenn er "in die Pedale tritt"?

Lösung:
Gegeben: Masse m=70Kg  Hebelarm a=20cm=0,2m 
Gesucht: F,M
Formeln:  F=Masse*Erdbeschleunigung → F=m*g 
          M=Kraft*Hebelarm          → M=F*a
Rechnung:  1) 70Kg*9,81m/s²=686,7N
           2) 686,7N*0,2m=137,34Nm

Antwort: Seine Gewichtskraft ist 686,7N und das Drehmoment beträgt 137,34Nm.

[Bearbeiten] Rotationsenergie und Trägheitsmoment

Satz von Steiner, Beispielkörper

[Bearbeiten] Drehimpuls und Trägheitstensor

Drehimpulserhaltungssatz, Hauptachsen, raumfeste Achsen, Diagonalisierung und Trägheitsellipsoid

[Bearbeiten] Kreiselbewegungen: Nutation und Präzession

Kräftefreier Kreisel, Drehachse und Figurenachse, Kreisel mit äußerem Drehmoment

[Bearbeiten] Mechanik deformierbarer Medien

Dehnung, Stauchung, Scherung, Drillung, Biegung

[Bearbeiten] Der Elastizitätsmodul und das Hooke'sche Gesetz

Herleitung des Hooke'schen Gesetzes für Festkörper, verschiedene Materialien, Dehnungs-Spannungs-Diagramm

[Bearbeiten] Querkontraktion und Poisson-Zahl

Querkontraktion und Zugspannung

[Bearbeiten] Kompressibilität und Kompressionsmodul

[Bearbeiten] Schub-, Scher- und Torsionsmodul

[Bearbeiten] Balkenbiegung

Einseitige und zweiseitige Einspannung, Punktlast, Linienlast, Flächenlast, Profil und Flächenträgheitsmoment

[Bearbeiten] Hydrostatik

Deformierbare Körper, Flüssigkeiten, Gase

[Bearbeiten] Druck und Auftrieb

Herleitung des Gesetzes von Archimedes

[Bearbeiten] Kompressibilität

[Bearbeiten] Kräfte an Grenzflächen

Kohäsionskräfte, Oberflächenspannung und -energie, Beispiel Seifenblase, Adhäsion, Kapillarität,

[Bearbeiten] Reibung an Grenzflächen

Coulomb-Reibung, Rollreibung, Stokes-Reibung, Newton-Reibung

[Bearbeiten] Hydro- und Aerodynamik

Strömungsfeld, Stromlinien, ideale und viskose Flüssigkeiten, laminare und turbulente Strömungen

[Bearbeiten] Ideale Flüssigkeiten

[Bearbeiten] Euler-Gleichung

Bewegungsgleichung für Teilchen in idealen Flüssigkeiten

[Bearbeiten] Kontinuitätsgleichung

Herleitung der Kontinuitätsgleichung

[Bearbeiten] Bernoulli-Gleichung

Staudruck, dynamischer Druck, hydrostatisches Paradoxon

[Bearbeiten] Dynamische Zähigkeit (Viskosität)

Laminares Strömungsprofil

[Bearbeiten] Strömungswiderstand

Gesetz von Hagen-Poiseuille

[Bearbeiten] Navier-Stokes-Gleichung

Reynolds-Zahl, Froude-Zahl, Mach-Zahl

[Bearbeiten] Turbulente Strömungen

Kritische Reynolds-Zahl, Übergang laminare und turbulente Strömungen

[Bearbeiten] Umströmte Körper

Prandtl-Grenzschicht, dynamischer Auftrieb, Magnus-Effekt

[Bearbeiten] Quellen

  • [1] Skripten von Prof. Gross, TU München
  • weitere folgen

[Bearbeiten] Weiteres Kursmaterial


[Bearbeiten] Teilnehmer


Betreuer: StudentT

Von „http://de.wikiversity.org/wiki/Kurs:Experimentalphysik_1“
Persönliche Werkzeuge