Kurs:Funktionentheorie/Kurven
Einführung
[Bearbeiten]In der Mathematik ist eine Kurve (von lat. curvus „gebogen, gekrümmt“) ein eindimensionales Objekt in einer zweidimensionalen Ebene (d.h. eine Kurve in der Ebene) oder in einem höherdimensionalen Raum (siehe Raumkurve).
Parameterdarstellungen
[Bearbeiten]- Mehrdimensionale Analysis: Eine stetige Abbildung ist eine Kurve im .
- Funktionentheorie: Eine stetige Abbildung ist ein Weg im (siehe auch Integrationsweg).
Erläuterungen
[Bearbeiten]Eine Kurve/ein Weg ist eine Abbildung. Dabei muss man die Spur des Weges bzw. das Bild eines Weges von dem Graph der Abbildung unterscheiden. Ein Weg ist (abweichend von der Umgangssprache) eine stetige Abbildung von einem Intervall in den betrachteten Raum (z.B. oder ).
Beispiel 1 - Plot
[Bearbeiten]
Beispiel 1 - Kurve als Lösungsmenge einer Gleichung
[Bearbeiten]|
bzw. . Bestimmen Sie für die Kurve alle mit |
Beispiel 1 - Berechnung der Lösungsmenge
[Bearbeiten]Da und auch gilt, muss für eine Lösung auch und damit gelten.
Plotten Sie nun den Graphen von und (z.B. in Maxima CAS, Geogebra, CAS4Wiki).
Beispiele 2
[Bearbeiten]Die Abbildung
beschreibt den Einheitskreis in der Ebene .
beschreibt den Einheitskreis in der Gaußschen-Zahlenebene .
Beispiele 3
[Bearbeiten]Die Abbildung
beschreibt eine Kurve mit einem einfachen Doppelpunkt bei , entsprechend den Parameterwerten und .
Richtungssinn
[Bearbeiten]Durch die Parameterdarstellung erhält die Kurve einen Richtungssinn in der Richtung wachsenden Parameters.[1][2]
Spur Kurve eines Weges
[Bearbeiten]Die Spur oder Kurve eines Weges bzw. ist das Bild eines Weges
- .
Unterschied - Graph und Kurve
[Bearbeiten]Für einen Weg ist die Spur oder die Kurve eine Teilmenge von , während der Graph der Funktion ist.
Aufgabe - Plot Graph und Kurve
[Bearbeiten]Plotten Sie mit CAS4Wiki den Graphen und die Kurve von:
Animation der Spur
[Bearbeiten]Die folgende Animation zeigt die Animation einer Abrollkurve von zwei Kreisen.
Kurven in Geogebra
[Bearbeiten]Erzeugen Sie zunächst einen Schieberegeler für die Variable und zwei Punkte bzw. und erzeugen Sie mit die Summe der beide Ortsvektoren von und . Analysieren Sie die Parametrisierung der Kurven. Geogebra:
K_1:(2*cos(t),2 * sin(t)) , K_2:(cos(3*t),sin(3*t)) , K: K_1+K_2
Siehe auch interaktives Beispiel in Geogebra
Gleichungsdarstellungen
[Bearbeiten]Eine Kurve kann auch durch eine oder mehrere Gleichungen in den Koordinaten beschrieben werden. Die Lösungsmenge der Gleichungen stellt die Kurve dar:
- Die Gleichung beschreibt den Einheitskreis in der Ebene.
- Die Gleichung beschreibt die oben in Parameterdarstellung angegebene Kurve mit Doppelpunkt.
Wird die Gleichung durch ein Polynom gegeben, nennt man die Kurve algebraisch.
Funktionsgraphen
[Bearbeiten]Funktionsgraphen sind ein Spezialfall beider oben angegebenen Formen: Der Graph einer Funktion
kann entweder als Parameterdarstellung oder als Gleichung dargestellt werden, wobei die Lösungsmenge der Gleichung die Kurve durch darstellt.
Wird in der Schulmathematik von Kurvendiskussion gesprochen, so meint man üblicherweise nur diesen Spezialfall.
Geschlossene Kurven
[Bearbeiten]Geschlossene Kurven sind stetige Abbildungen mit . In der Funktionentheorie benötigen wir Kurven in , die stetig differenzierbar sind. Diese nennt man Integrationswege.
Umlaufzahl in den komplexen Zahlen
[Bearbeiten]Glatten geschlossenen Kurven kann man eine weitere Zahl zuordnen, die Umlaufzahl, die für eine nach der Bogenläge parametrisierte Kurve durch
gegeben ist. Der Umlaufsatz besagt analog zu einer Kurve im , dass eine einfache geschlossene Kurve die Umlaufzahl oder besitzt.
Kurven als eigenständige Objekte
[Bearbeiten]Kurven ohne umgebenden Raum sind in der Differentialgeometrie relativ uninteressant, weil jede eindimensionale Mannigfaltigkeit diffeomorph zur reellen Geraden oder zur Einheitskreislinie ist. Auch Eigenschaften wie die Krümmung einer Kurve sind intrinsisch nicht feststellbar.
In der algebraischen Geometrie und damit zusammenhängend in der komplexen Analysis versteht man unter „Kurven“ in der Regel eindimensionale komplexe Mannigfaltigkeiten, oft auch als Riemannsche Flächen bezeichnet. Diese Kurven sind eigenständige Studienobjekte, das prominenteste Beispiel sind die elliptischen Kurven. Siehe Kurve (algebraische Geometrie)
Historisches
[Bearbeiten]Das erste Buch der Elemente von Euklid begann mit der Definition
- Ein Punkt ist, was keine Teile hat. Eine Kurve ist eine Länge ohne Breite.
Diese Definition lässt sich heute nicht mehr aufrechterhalten, denn es gibt zum Beispiel Peano-Kurven, d. h. stetige surjektive Abbildungen , die die gesamte Ebene ausfüllen. Andererseits folgt aus dem Lemma von Sard, dass jede differenzierbare Kurve den Flächeninhalt null, also tatsächlich wie von Euklid gefordert keine Breite hat.
Interaktives Darstellungen von Kurven in Geogebra
[Bearbeiten]- Tangentialvektor einer Kurve im für eine Kurve mit Tangentialvektor
- Abrollkurven Fahrradreflektoren als Beispiel für Kurven - Zykloide
- Abrollkurve für Beispiel 2
Siehe auch
[Bearbeiten]Literatur
[Bearbeiten]- Ethan D. Bloch: A First Course in Geometric Topology and Differential Geometry. Birkhäuser, Boston 1997.
- Wilhelm Klingenberg: A Course in Differential Geometry. Springer, New York 1978.
Einzelnachweise
[Bearbeiten]- ↑ H. Neunzert, W.G. Eschmann, A. Blickensdörfer-Ehlers, K. Schelkes: Analysis 2: Mit einer Einführung in die Vektor- und Matrizenrechnung. Ein Lehr- und Arbeitsbuch. 2. Auflage. Springer, 2013, lSBN 978-3-642-97840-1, 23.5
- ↑ H. Wörle, H.-J. Rumpf, J. Erven: Taschenbuch der Mathematik. 12. Auflage. Walter de Gruyter, 1994, lSBN 978-3-486-78544-9
Weblinks
[Bearbeiten]
Seiteninformation
[Bearbeiten]Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Wiki2Reveal
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Funktionentheorie' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Kurven
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.
Wikipedia2Wikiversity
[Bearbeiten]- Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:
- Datum: 11.11.2018
- Wikipedia2Wikiversity-Konverter: https://niebert.github.com/Wikipedia2Wikiversity

![{\displaystyle f:[a,b]\to \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0aa7343202f20f61fce7387e37f8bd190b810520)

![{\displaystyle f:[a,b]\to \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d7143a5f03fb51f263466f372bc3b52b227d69c)























![{\displaystyle \gamma :[a,b]\to \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ba8e67ece48ed58462781818669d29170ae4809)
![{\displaystyle \gamma :[a,b]\to \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cac70dec799b73a718bdc3431587a65f829bf03b)

![{\displaystyle \gamma :[a,b]\to \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1d326a550ef41246054e0311de07e1375d535f3)

![{\displaystyle {\begin{array}{rrcl}\gamma :&[0,6\pi ]&\rightarrow &\mathbb {R} ^{2}\\&t&\mapsto &\gamma (t)=\left(3\cdot \cos(t),\sin(t)\right)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7f9e5e15461170a62af8eb626ff2013e4ef6bea)
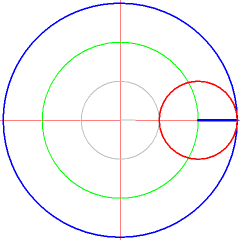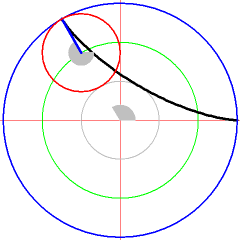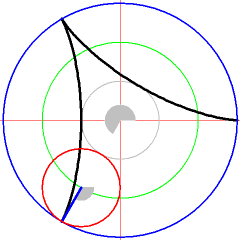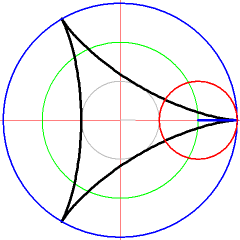
![{\displaystyle t\in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbc9ed8510c75442ce1d2e73f021258fc7e04c6)











![{\displaystyle \gamma \colon [a,b]\to \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e085dcf244196598d1b9b015bdbfbe624800679)








![{\displaystyle \gamma ':[a,b]\to \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4985098cd3850bb2c8aa01b67e46fb0e4541a464)
