Kurs:Mathematische Modellbildung/Themen/2023-24 Wintersemester/Eisflächen und Effekt auf den Meeresspiegel
Prognose über das Schmelzen der Eismassen und den Verlust an Lebensraum durch den steigenden Meeresspiegel
[Bearbeiten]zurück zur Übersichtsseite WS 23-24
Anmerkungen (AH) 05.02.2024
[Bearbeiten]- Die Bearbeitung des Thema sieht fortgestritten aus, die graphische Umsetzung mit der Lankare ist beeindruckend.
- Herr Heusel (und Decker) sind in KLIPS zur falscher Prüfung angemeldet. Bitte Emails diesbezüglich beachten.
Gruppenteilnehmer
[Bearbeiten]- Decker, Benjamin
- Heusel, Luca
- Öztürk, Behcet
Hinführung und Motivation
[Bearbeiten]Da Aufgrund der steigenden Temperaturen immer mehr Gletscher und Eisflächen schmelzen, wird in absehbarer Zeit ein immer stärkeres Ansteigen des Meeresspiegels zu beobachten sein. Dies hat nicht nur einen Effekt auf die vom Eis reflektierte Strahlung, sondern auch in Kombination mit dem ansteigenden Meerwasserspiegel, einen Verlust an Lebensraum an den Küstengebieten des Festlands. Ebenso sind davon Inseln betroffen, da diese im Vergleich zum Meerwasser relativ betrachtet absinken und somit von Wasser verdeckt werden.
Im Nachfolgenden Modell wollen wir uns zunächst dem Abschmelzen der Eisvolumina widmen und im Anschluss betrachten, mit welchem Lebensraumverlust an gewählten Beispielen zu rechnen ist, sollte das gesamte Eis der Erde abschmelzen. Dazu werden wir den Verlust an eine Fünfjahresprognose binden, welche aus unseren Berechnungen stammt.
Abschließend wollen wir einen Blick in die Zukunft wagen, indem wir uns die betroffenen Gebiete anschauen, welche von dem Wasseranstieg in extremem Ausmaß betroffen sind und welche Konsequenzen dies etwa für Kultur, Wirtschaft und die Artenvielfalt haben könnte.
Ziel der Modellierung
[Bearbeiten]Eine Sensibilisierung der Politik zum Einhalten und Erreichen der Klimaziele ist eines der Hauptziele dieser Modellierung. Neben der Politik im Allgemeinen, sollen auch Firmen dazu angeregt werden, von sich aus eine emissionsärmere Produktion anzustreben und somit stärker in die Eigenverantwortung genommen werden. Ebenso ist es Ziel dieser Modellierung Schüler*innen zur Selbstreflektion über ihr eigenes Konsumverhalten anzuregen, da ein überhöhter Konsum mit einem erhöhten ökologischen Fußabdruck einhergeht, welcher durch die damit verbundenen Kohlenstoffdioxid-Emissionen den Anstieg der Temperatur und somit das Abschmelzen der Eisflächen begünstigt.
Zuordnung zu den Sustainable Development Goals
[Bearbeiten]
Je weniger Eisflächen global vorhanden sind, desto weniger Strahlung wird reflektiert und desto mehr Strahlung trifft die Erde, was wiederum den Temperaturanstieg indirekt begünstigt. Dementsprechend wird es durch diese positive Rückkopplung immer wärmer, was die psychische und physische Gesundheit beeinträchtigen kann.
Jede Firma produziert in einem Maße Güter oder Dienstleistungen, welche mit Emissionen verbunden sind. Dementsprechend, können diese selbstständig ohne Intervention der Politik dafür sorgen, ihre Emissionen zu verringern und insgesamt nachhaltiger zu agieren.
Da die schmelzenden Eisflächen als Kipppunkt für den Klimawandel gelten, sind diese somit auch von elementarer Bedeutung. Sind die Eisschilde Grönlands abgeschmolzen, so steigt nicht nur der Wasserspiegel global an, sondern es wird auch weniger Strahlung reflektiert.
Durch den Anstieg des Wasserspiegels, durch Süßwasser, wird das marine Ökosystem gestört und dementsprechend kann es zu einem Artensterben aufgrund des Süßwassereintrags kommen. Da Ökosysteme immer einem gewissen Gleichgewicht unterliegen, oftmals durch sogenannte Schlüsselarten, kann dieses Gleichgewicht nachhaltig oder sogar unumkehrbar gestürzt werden, was zu einem Verlust unterschiedlichster Ökosystemverbände führen kann.
Durch steigende Meeresspiegel geht auch am Festland Lebensraum verloren, was zu einer Migration von Mensch, Tier und Parasiten führt. Dies kann nachhaltig dafür sorgen, dass sich Menschen vermehrt auf der selben Fläche sammeln, was Virusmutationen begünstigt und so die FItness der Gesamtpopulation negativ beeinträchtigen kann.
Durch die sich anbahnende Klimakatastrophe kann es dazu kommen, dass Menschen aus den von den extremen Klimabedingungen geplagten Regionen flüchten. Dies hat zur Folge, dass eine Migration von Menschen außenpolitisch und auch innenpolitisch adäquat und humanistisch gehandhabt werden muss. Damit dies möglich ist, müssen Institutionen geplant und geschaffen werden, welche sich kompetent dieser Problematik annehmen können.
Der Klimawandel betrifft den ganzen Planeten und somit jede Nation. Dementsprechend müssen alle Nationen zusammenarbeiten, damit die Klimakatastrophe abgewendet beziehungsweise vermindert werden kann. Daher gilt es gemeinsame Abkommen und Ziele zu formulieren, damit nachfolgende Generationen einen zukunftsfähigen und bewohnbaren Planeten vorfinden können.
Niveauzuordnung
[Bearbeiten]Im Folgenden sollen anhand der drei Modellierungszyklen gezeigt werden, welche Schritte und Methoden für welchen Zyklus angedacht sind:
Modellierungsplan
[Bearbeiten]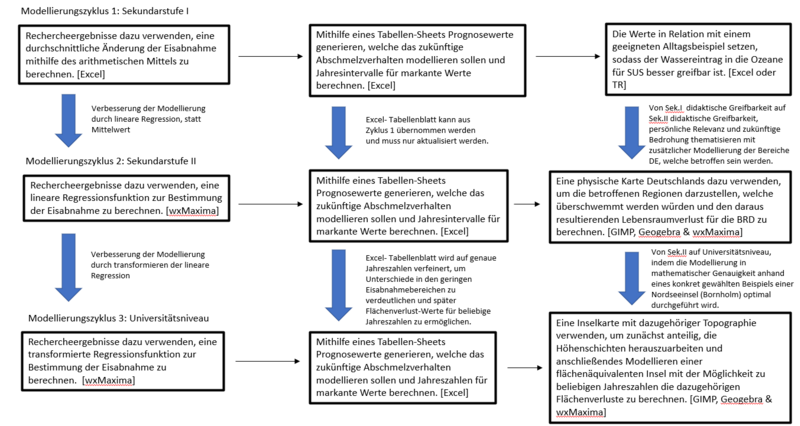
Zyklus I: Sekundarstufe I
[Bearbeiten]Modell zur Bestimmung der zukünftig schmelzenden Eismenge in Gigatonnen (GT), anhand einer Annäherungsfunktion. Diese Funktion soll eine Vereinfachung einer Regression darstellen (geeignet ab Klassestufe 7/8), indem der funktionale Zusammenhang zwischen Jahr (x-Achse) und bereits abgeschmolzener Eismasse (y-Achse) untersucht wird:
- Durchschnittsänderung der y-Werte ermitteln
- Prognose zukünftig schmelzender Eismasse anhand einer linearen Funktion
- Ermittlung des Jahres, ab wann kein Eis mehr vorhanden sein wird
- Süßwassereintrag aus geschmolzener Eismasse berechnen ( Exkurs: Physik ) und Vergleich mit füllbaren Schwimmbadbecken (Greifbarkeit der Wassermenge, welche in die Ozeane entlassen wird)
Zyklus II: Sekundarstufe II
[Bearbeiten]Modell zur Bestimmung der zukünftig schmelzenden Eismenge in Gigatonnen (GT), anhand einer Reggressionsfunktion. Diese Funktion soll eine lineare Regression sein, welche im Kern auf dem Prinzip der kleinsten Quadrate basiert (geeignet ab Klassestufe 10/11). Dies kann in einer Klasse mit der Regressionsfunktion in Excel oder LibreOffice Calc realisiert werden, wird hier allerdings manuell durchgeführt:
- Datenerhebung aus Recherche
- Übertrag in Tabellenform (Excel)
- lineare Regressionsfunktion ermitteln (Maxima)
- Prognose zukünftig schmelzender Eismasse anhand der ermittelten Regressionsfunktion (Excel)
- Ermittlung des Jahres, ab wann kein Eis mehr vorhanden sein wird (Excel)
- SLE verwenden, um Flächenverlust Deutschlands im Norden Deutschlands zu ermitteln.
- Visualisierung mit GIF
Zyklus III: Universitätsniveau
[Bearbeiten]Modell zur Bestimmung der zukünftig schmelzenden Eismenge in Gigatonnen (GT), anhand einer Transformationsfunktion. Diese Funktion soll eine nichtlineare Regression sein, welche im Kern auf dem Prinzip des Transformationsansatzes basiert:
- Datenerhebung aus Recherche
- Übertrag in Tabellenform (Excel)
- Berücksichtigung der Schmelzrate des Eises anhand der steigenden Durchschnittstemperatur der Erde
- nichtlineare Regressionsfunktion ermitteln
- Prognose zukünftig schmelzender Eismasse anhand der ermittelten transformierten Regressionsfunktion
- Ermittlung des Jahres, ab wann kein Eis mehr vorhanden sein wird
- Modellierung einer Nordseeinsel (bspw. Bornholm) mit Geogebra mit der zur Insel gehörigen Topographie und dem damit verbundenen Flächenverlust
Verwendete Software
[Bearbeiten]- Excel (alternativ LibreOffice Calc)
- wxMaxima (GUI for Maxima)
- GeoGebra Classic
- GIMP 2.10.36
Recherche und wichtige Umrechnungen
[Bearbeiten]| Gletscher | Eiskappen | Gletscher und Eiskappen | Grönland Eisschild | Antarktis Eisschild | |
|---|---|---|---|---|---|
| Anzahl | > 160 000 | 70 | 1 | 1 | |
| Fläche (10^6 km^2) | 0,43 | 0,24 | 0,68 | 1,71 | 12,37 |
| Volumen (10^6 km^3) | 0,08 | 0,10 | 0,18 | 2,85 | 25,71 |
| SLE (sea level rise equivalent, m) | 0,24 | 0,27 | 0,51 | 7,2 | 61,1 |
| Jährliches SLE (mm/yr) | 1,9 | 1,4 | 5,1 |
Diese Studien liefern unsere Werte, mit denen wir die Eismasse in Gigatonnen (GT) berechnen können und fortan die abschmelzenden Eismassen betrachten werden, bis diese in der Zukunft endgültig abgeschmolzen sind.
| Jahresintervall | Verhalten der Eismasse in Gigatonnen pro Jahr |
|---|---|
| 1992 - 1996 | -113 |
| 1997 - 2001 | -299 |
| 2002 - 2006 | -405 |
| 2007 - 2011 | -634 |
| 2012 - 2016 | -665 |
Diese Studie liefert einen Überblick über das Abschmelzverhalten der gesamten globalen Eismasse in Gigatonnen (GT), worauf wir unsere Prognose über das zukünftige Schmelzverhalten aufbauen werden. Diese wird ebenso in Intervallen zu je fünf Jahren sein.
Um aus einem Volumen () an Eis ihre zugehörige Masse (GT) zu berechnen, wird folgende Formel Verwendet:
,
wobei gilt: : Masse des Eises (GT), : Volumen des Eises (), : Dichte des Eises (). [3]
Somit ergibt sich für die obigen Volumina der Eismassen folgende Massenwerte:
| Eisregion | Masse (GT) |
|---|---|
| Gletscher | 73 336 |
| Eiskappen | 91 670 |
| Gletscher und Eiskappen | 165 006 |
| Grönland Eisschild | 2 612 595 |
| Antarktis Eisschild | 23 568 357 |
Modellierungszyklus I
[Bearbeiten]Im ersten Schritt wurde aus den Abnahmewerten aus Tabelle 2 mit dem arithmetischen Mittel ein Durchschnittswert berechnet, womit in diesem Zyklus die weitere Eisabnahme modelliert wird:
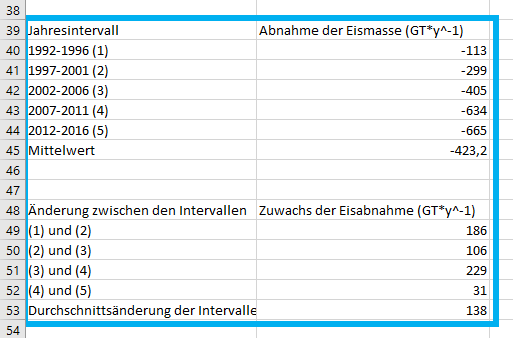
Im zweiten Schritt wurde die bereits gemessene und die nun neu ermittelte Abnahmerate tabellarisch dargestellt.
Hier wurde ein erster Versuch gewagt, die Eisabnahme mit einzelnen Jahreszahlen darzustellen und anschließend aufzukumulieren. Da dies jedoch für eine unverhältnismäßig große Datei gesorgt hätte und es uns in erster Linie nicht um die exakte Jahreszahl geht, sondern viel mehr um einen etwas größeren Zeitraum, in welchem die Abnahme der jeweiligen Eismasse beendet wäre, haben wir uns für eine Vergrößerung des Zeitraumes auf eine Intervallgröße von je 5 Jahren geeinigt, um unsere Ergebnisse ähnlich der Studie aus Tabelle 2 ausdrücken zu können.
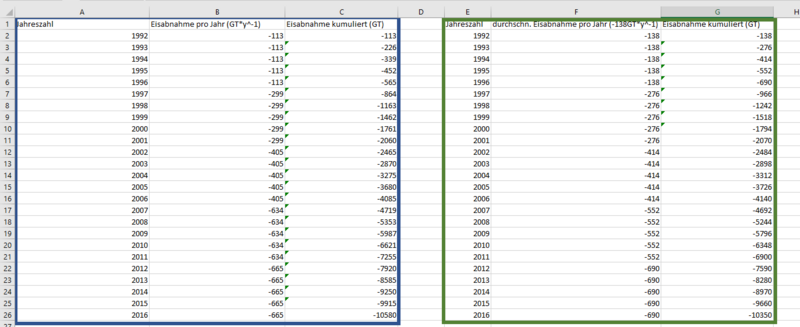
Im dritten Schritt haben wir die Intervalle wie oben beschrieben auf 5 Jahre erhöht und anschließend zunächst die Abnahme für das jeweilige 5-Jahresintervall aufkumuliert und im Anschluss eine Gesamtkumulation der insgesamt abgeschmolzenen Masse berechnet. So kann auf einen Blick erkannt werden, in welchem Jahr eine gewisse Gesamtmasse bereits abgeschmolzen wäre. Da die Tabelle sehr viele Zeilen umfasst, wird hier nur ein Ausschnitt der Tabelle gezeigt, damit das Prinzip unserer Rechnung nachempfunden werden kann. Eine Auflistung von markanten werden ist in Tabelle 4 zu finden.

Um nicht die ganze 277 Zeilen umfassende Tabelle aus Excel abbilden zu müssen, wurden in Tabelle 4 die markantesten Werte zusammengetragen. So ist zu erkennen, dass im Jahre 3367 die weltweite Eismasse abgeschmolzen wäre.
| Eisregion | 5-Jahresintervall (Jahr+4) |
|---|---|
| Gletscher | 2057 |
| Eiskappen | 2067 |
| Grönland Eisschild | 2422 |
| Antarktis Eisschild | 3292 |
| Alle | 3367 |
Die insgesamt 26.345.958 GT Eismasse wiegen offensichtlich genauso viel im geschmolzenen Zustand als Wasser mit 26.345.958 GT Wasser, welche ihrerseits ein Volumen von 26.345.958 km^3 einnimmt. Rechnet man dies in Liter um, so erhält man:
Um die nun erhaltenen Liter Wasser besser für SUS größentechnisch einordnen zu können, überführen wir diese in ein bekanntes Alltagsbeispiel, indem wir das erhaltene Volumen dazu nutzen Schwimmbecken zu füllen:
Dabei verwenden wir ein Schwimmbecken mit einer Länge von 50 m, einer Breite von 20 m und einer Tiefe von 2 m:
Schwimmbäder
In Worten: 13 Billionen 172 Milliarden 979 Millionen Schwimmbäder mit einem Fassungsvermögen von 2 Millionen Liter Wasser könnte man also füllen, wenn die gesamten Eismassen der Erde abschmelzen würden.

Modellierungszyklus II
[Bearbeiten]Im ersten Schritt wurde aus den Werten aus Tabelle 2 eine lineare Regression nach dem Prinzip der kleinsten Quadrate durchgeführt und damit eine Regressionsfunktion in wxMaxima berechnet, was in Abbildung 5 zu sehen ist.
Die Regression wurde in 4 Schritten durchgeführt:
1. Formulierung des Minimierungsproblems (Zeile %01)
2. Differenzierung nach je einer Variable (b dann m) und Termvereinfachungen (Zeilen %02-%05)
3. Lineares Gleichungssystem lösen (Zeile %06)
4. Regressionsgerade anzeigen (Zeile %07)

Im Anschluss haben wir die Regressionsgerade einmal zur Veranschaulichung geplottet.

Betrachtet man nun Abbildung 7, so erkennt man, dass das erste 5-Jahresintervall mit einer jährlichen Eisabnahme von 135,4 GT beginnt und es anschließend pro Intervall 143,9 GT mehr abnehmen wird.

In Abbildung 8 ist in der linken Tabelle (blau) wie in Zyklus 1 zunächst die jährlichen und anschließend kumulierten Abnahmewerte der Eismasse aus Tabelle 2 zu sehen. Auf der rechten Seite (grün) wurden die Prognosewerte aus der Regressionsfunktion abgebildet. Diese werden auch dazu verwendet wie in Zyklus 1 eine weitere Tabelle zu erstellen, welche in 5-Jahresintervallen die Gesamtabnahme der Eismasse in aufkumulierten Werten anzeigt.

In Abbildung 9 sieht man wie in Zyklus 1 einen Ausschnitt der Tabelle, welche die Gesamtabnahme der Eismasse zeigt. Die markanten Werte findet man in Tabelle 5 (s.u.).

| Eisregion | 5-Jahresintervall (Jahr+4) |
|---|---|
| Gletscher | 2057 |
| Eiskappen | 2067 |
| Grönland Eisschild | 2412 |
| Antarktis Eisschild | 3267 |
| Alle | 3342 |
Mit der Fotobearbeitungssoftware GIMP wurde in einer physischen Karte Deutschlands jene Regionen eingefärbt, welche gemäß ihrer Topographie auf einem Höhenniveau von weniger als 50 Höhenmetern liegen und keine geographischen Barrieren aufweisen. Dies hat den Hintergrund, dass sämtliche Eismassen, sofern sie vollständig abschmelzen einen Meeresspiegelanstieg von 68,81m bewirken würden. Da die nächste eingefärbte Region Höhenmeter bis einschließlich 100m beinhaltet, kann nicht mit Sicherheit gesagt werden, welche Flächen betroffen wären, daher wurde sich nur auf die Flächen konzentriert, welche von einem Meeresspiegelanstieg von 68,81m garantiert betroffen werden würden. Dies hat natürlich zur Folge, dass man hier nur von einer betroffenen Mindestfläche reden kann und dies nur eine grobe Annäherung darstellt. Die somit festgelegte Fläche ist in dem GIF in Abbildung 10 zu sehen und blinkt blau.
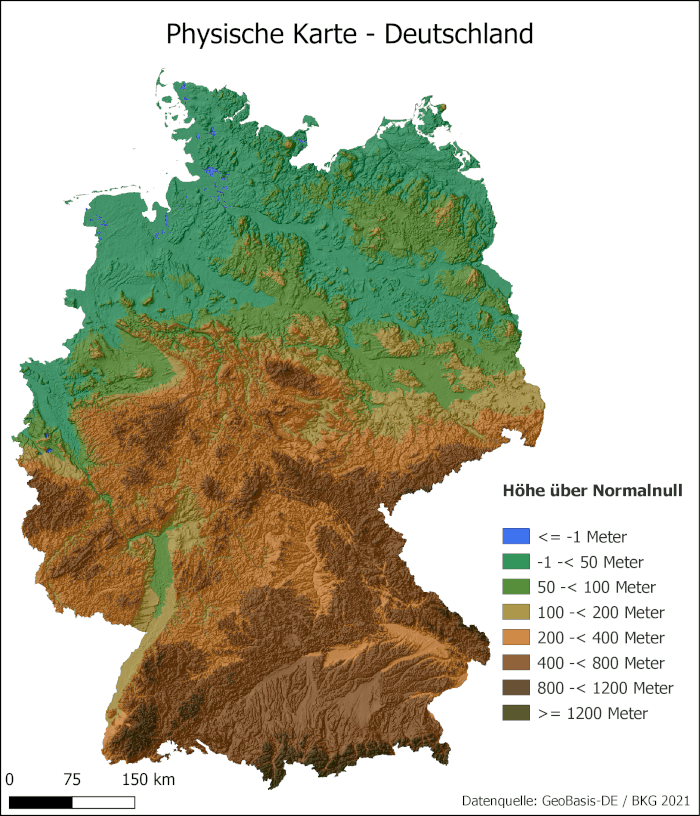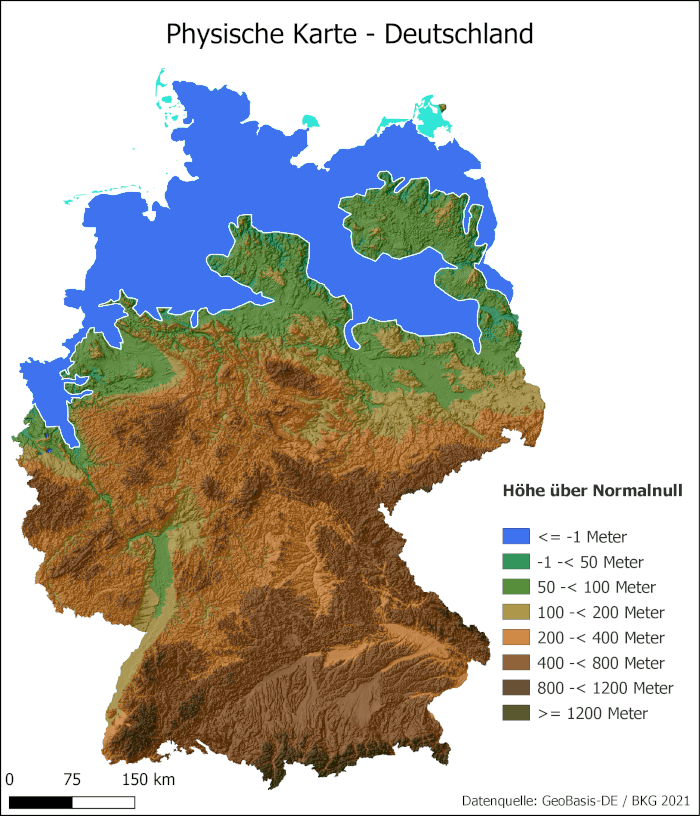
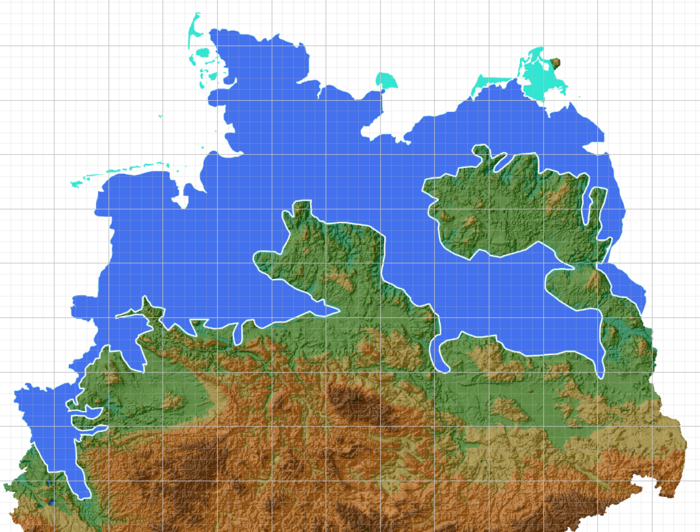
Mit Geogebra wurde das Raster so ausgelegt, dass jedes Quadrat mit einer Länge von 10 Kilometern eine Fläche von 100 Quadratkilometern abdeckt.

Die Fläche wurde nicht berechnet, sondern durch das Auslegen eines Rasters grob abgezählt, um zeitsparend eine greifbare Dimension für SUS zu erschaffen, welche ohne komplizierte und lange Rechnungen auskommt. Dies hat zum Vorteil, dass es sich durch Aufteilen des Rasters organisatorisch schnell zählen lässt.
Anmerkung: Man hätte alternativ auch einzelne Quadrate, durch welche die Ränder der Fläche verlaufen berechnen können, indem man bspw. den Rand eines jeden Quadrates durch ein Polynom annähert und die darunterliegende Fläche mittels Integralrechnung bestimmt. Dies hat angesichts der hohen Anzahl an "Ränderquadraten" zwar den Vorteil einer deutlich höheren Genauigkeit, aber dementsprechend einen massiv höheren Zeitaufwand, welchen man in der Schule in der Regel nicht aufbringen kann.
In Abbildung 13 sind die Zählwerte des Rasters aus Geogebra zu sehen. Dabei wurde immer zuerst die Anzahl der Festlandquadrate gezählt und notiert und anschließend die Inselquadrate dahintergeschrieben, sofern vorhanden und durch ein Ampersand voneinander getrennt.
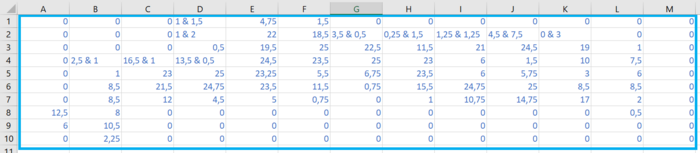
Anschließend wurden die Werte aufaddiert und als Spaltensummen notiert, was in Abbildung 14 zu sehen ist. Die Inselquadrate wurden aufgrund ihrer geringen Anzahl außerhalb der Datei zusammengerechnet. Die Ergebnisse sind in Tabelle 6 (s.u.) noch einmal abgebildet.

In Tabelle 6 wurden die Ergebnisse der Zählung noch einmal zusammengetragen und anschließend in ihre Flächenzahlen umgerechnet. Betrachtet man nun die Gesamtfläche Deutschlands, welche sich auf gerundet 357 600 Quadratkilometer beläuft [5] , so kann man die minimale betroffene Fläche prozentual bestimmen:
| Betroffene Region | Gezählte Quadrate | betroffene Fläche (Quadratkilometer) |
|---|---|---|
| Inseln | 19,75 | 1975 |
| Festland | 773,75 | 77 375 |
| Festland & Inseln | 793,5 | 79 350 |
Zusammenfassend kann also gesagt werden, dass Deutschland bei vollständigem Abschmelzen der Eismassen mindestens ein Flächenverlust von etwa 28,52 % droht, sollte die Prognose eintreten.
Modellierungszyklus III
[Bearbeiten]Betrachtet man als treibenden Faktor für die Abschmelze der globalen Eismassen die Erwärmung der Erde, so kann man bei jüngster Entwicklung davon ausgehen, dass zukünftig die Erderwärmung nicht durch eine lineare Funktion beschrieben werden kann. Diese wird laut ECI und der Oxford Universität mehr durch einen nichtlinearen Zusammenhang multifaktoriell beschrieben. [6]
Wir nehmen weiter an, dass sich die Erwärmung der Erde direkt proportional auf die abschmelzende Eismasse auswirkt und betrachten nun, wie die Eisschmelze aussehen würde, wenn sie mit steigender Erderwärmung mitwachsen würde. Dazu wird an dieser Stelle ein nicht linearer Zusammenhang in Form einer Potenzfunktion angenommen:
In Abbildung 15 wurden zunächst die Werte aus der ursprünglichen Studie mit dem natürlichen Logarithmus derart transformiert, dass sich im Anschluss Werte einer Funktion ergeben, welche linearer Gestalt sind. Damit kann nach Berechnung der linearen Regressionsfunktion, wie es in Abbildung 16 nach dem Prinzip der "Summe der quadratischen Abweichungen" geschieht, eine Rücktransformation mithilfe der Exponentialfunktion durchgeführt werden, sodass die nun berechneten Parameter "a" und "b" in die Potenzfunktion eingesetzt werden können. Dies liefert und abschließend eine transformierte Regressionsfunktion, welche uns im dritten Zyklus unserer Prognosewerte liefern wird.

In Abbildung 16 sind die genauen Zahlen abgebildet, welche zur Parameterberechnung verwendet wurden. Es handelt sich hierbei aber noch um die Parameter " a' " und " b' ". Diese werden in Abbildung 15 wie oben beschrieben mit der Exponentialfunktion rücktransformiert.

In Abbildung 17 findet wie in den beiden ersten Zyklen ein kurzer Vergleich der beiden Wertemengen statt. In blau sind wie bisher die Studienwerte abgebildet und in grün die Werte aus der transformierten Regression.

In Abbildung 18 wird ein Ausschnitt der Wertetabelle gezeigt, um nachvollziehen zu können, wie diese sich aufkumulieren und wie die Tabelle strukturiert wurde. Da die Tabelle über 1000 Zeilen lang ist, kann sie nur ausschnittsweise abgebildet werden.
Zusätzlich wurde mit folgender Formel ein Faktor berechnet, welcher für unsere Zahlen ein "sea level equivalent" (SLE) liefert, der angibt, um wieviele Millimeter pro Jahresintervall der Meeresspiegel ansteigen wird.
Dieser wurde wie folgt berechnet:
Hierbei wird der Kehrwert eines Quotienten aus Gesamteismenge (GT) und Gesamtanstieg des Meeresspiegels (mm) gebildet. Dieser Faktor kann nun in Verbindung mit den kumulierten Eisabnahmewerten dazu verwendet werden, für beliebige Jahreszahlen die dazugehörigen SLE (mm) Werte zu prognostizieren. Die theoretische Grundlage dieser Rechnung basiert auf den Ergebnissen von Bethan Davies und ihren Umrechnungsformeln. [7]
Diese haben wir nur auf unsere Zahlenwerte angeglichen.
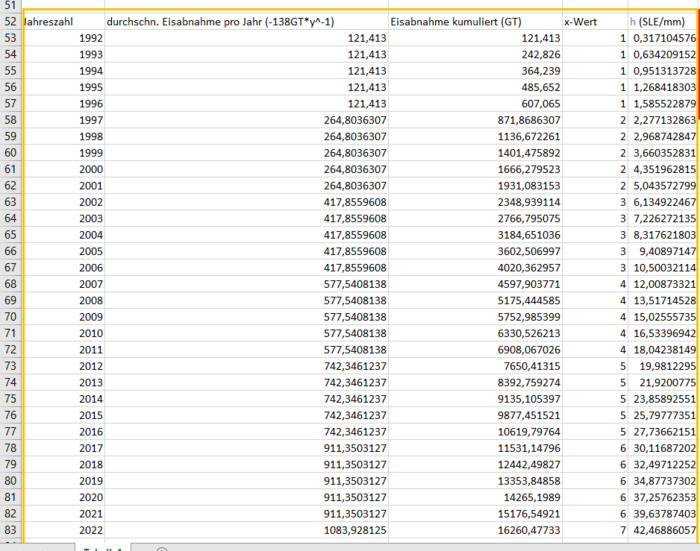
Aus der in Abbildung 18 erstellten Tabelle können nun markante Werte abgelesen werden. Diese wurden in Tabelle 7 einmal zusammengetragen.
| Eisregion | 5-Jahresintervall (Jahr+4) |
|---|---|
| Gletscher | 2057 |
| Eiskappen | 2065 |
| Grönland Eisschild | 2355 |
| Antarktis Eisschild | 3018 |
| Alle | 3074 |
Im Folgenden Abschnitt unserer Modellierung wollen wir uns einem konkreten Beispiel einer betroffenen Insel ansehen, welche Flächenverluste mit dem ansteigenden Meeresspiegel verbunden wären.
Mithilfe einer Website [8] , welche beim Anklicken der Insel an einer beliebigen Stelle den dazugehörigen Wert in Bezug auf Höhenmeter ausgeben kann, wird im Anschluss nun eine Insel modelliert, welche eine äquivalente Verteilung der Reliefs besitzt. Somit kann beim Ansteigen des Meeresspiegels bei dieser Insel eine Aussage getroffen werden, wieviel Grundfläche und Oberfläche verloren gehen würden.
In Abbildung 19 ist ein Ausschnitt aus der Datenbank zu sehen, welche die Insel Bornholm mit ihren topgrafischen Daten darstellt. Anhand dieser Insel werden wir unsere Modellierung durchführen.
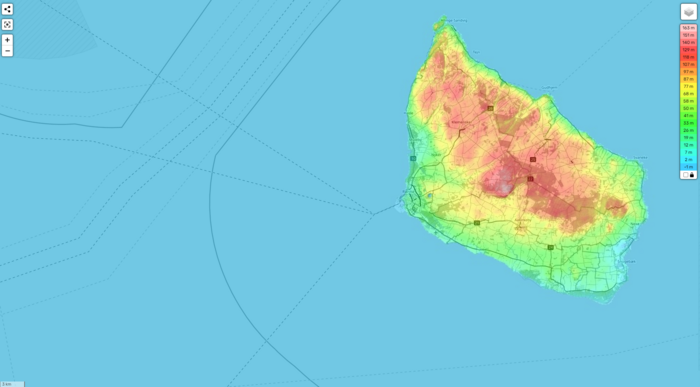
Zunächst benötigen wir aber ein zuverlässiges Rater, welches die Insel in messbare Flächenareale einteilt. Dazu wurde Die Geometriesoftware GeoGebra verwendet. Wir haben das Bild der Insel Bornholm in den Hintergrund eines Koordinatensystems gelegt und aufgrund der Größe der Insel, das Raster in eine obere und in eine untere Hälfte eingeteilt. In Abbildung 20 und Abbildung 21 sind die beiden Hälften jeweils abgebildet.
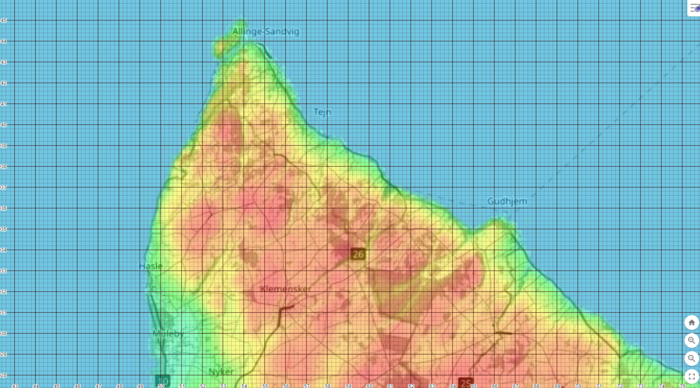

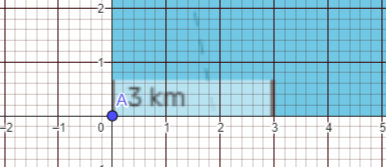
Um die Messbarkeit dieser durch das Raster entstandenen Quadratflächen gewährleiten zu können, wurde das Raster im Wesentlichen an den Maßstab des Datenbankausschnitts angelegt. Somit erhalten wir die in Abbildung 22 dargestellten Verhältnisse zwischen Maßstab und Quadraten. Somit entspricht ein Quadrat einer Fläche von einem Quadratkilometer.
In Abbildung 23 und Abbildung 24 sind die beiden Raster als Hintergrund in Excel eingefügt worden. Zusätzlich wurden die einzelnen Zellen von Excel an das Koordinatenraster aus GeoGebra angepasst, sodass immer mittig im Raster ein dazugehöriger Höhenwert für das Flächenquadrat eingetragen werden kann. Die Werte wurden mithilfe oben genannter Website erstellt, indem an markanten Punkten der Karte (etwa Straßennetz u.ä.) äquidistant in der Mitte des Quadrats Flächenwerte ausgegeben wurden. Die Website kann lediglich ganzzahlige Werte ausgeben, daher wird dies im fortführenden Modellierungsverlauf berücksichtigt.
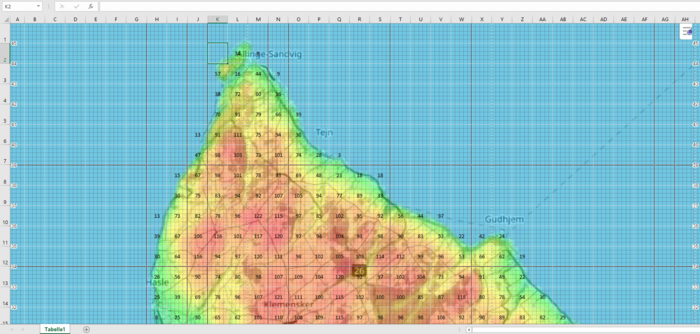

In Abbildung 25 und Abbildung 26 sind die Werte noch einmal ohne Hintergrund abgebildet, damit diese besser gelesen werden können.

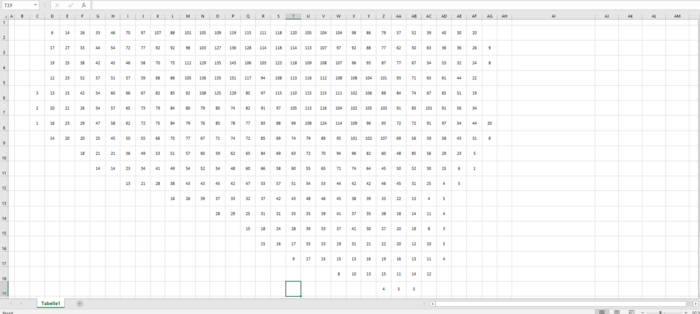
Im folgenden wurden alle Quadrate ähnlich wie in Zyklus 2 abgezählt und die damit verbundenen Flächenareale ausgerechnet. Die Berechnung unterliegt im Wesentlichen zwei Fehlern:
- Küstenregion bzw. Strandlinie
- Maßstabsfehler
Diese beiden Fehler wurden weitestgehend bereinigt. Die Küstenregion wurde durch Subtrahieren der anteilig zu viel gewerteten Miniquadrate an den echten Wert angeglichen. Der Maßstabsfehler wurde mit einem Ausgleichsfaktor bereinigt. Der nun verbleibende Messfehler beträgt ca. 1,2%. Wir rechnen in diesem Fall mit den von uns berechneten Werten weiter, was dazu führt, dass die Insel Bornholm im Vergleich mit unserem Literaturwert etwa 7,126 Quadratkilometer zu groß ausfällt. [9]
Die Auswertung und Korrekturen können in Abbildung 27 und Abbildung 28 eingesehen und nachvollzogen werden.

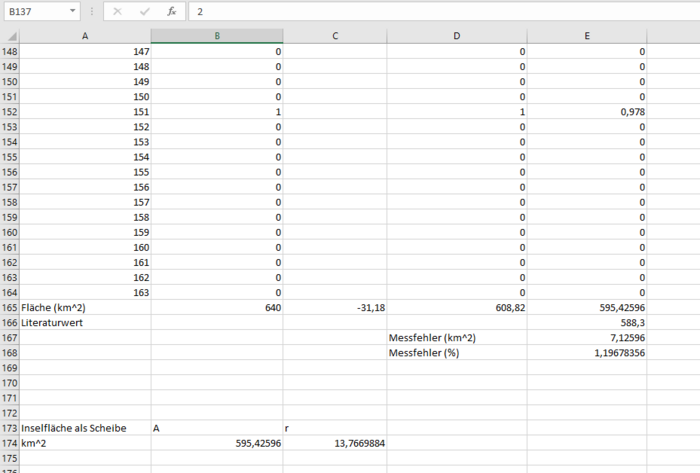
Um nun ein dreidimensionales Modell für eine Insel zu erstellen, werden wir die nun berechnete Gesamtfläche in Verbindung mit ihrer jeweiligen Zuordnung zu ihren Höhenniveaus (Höhenmeter) dazu verwenden, einzelne Kreisscheiben zu erstellen. Dazu wird eine äquivalente Insel als Kreis angenommen und in Abbildung 28 wurden bereits Gesamtfläche und Radius ebendieser Insel berechnet.
Die berechneten Kreisscheiben sollen sowohl die topografischen Höhenschichten darstellen, als auch anteilig den durch diese Scheibe beigetragenen Anteil zum Gesamtradius.
Im Anschluss wird von jeder Kreisscheibe der Mittelpunkt der Radiusstrecke berechnet, sodass abschließend durch ein "Verbinden" dieser Punkte mithilfe kubischer Splines ein Inselrelief entsteht, welche den Anteil jedes Höhenniveaus der Insel berücksichtigt.
Mit diesen Daten kann dann durch Erstellen eines Rotationskörpers sowohl das Volumen auch als die Inseloberfläche berechnet werden.
Letztlich wird durch eine horizontale Ebene und deren Schnittfläche mit dem Rotationskörper ebendieser in zwei Komponenten unterteilt, nämlich in sich unter der Wasseroberfläche befindlicher Inseloberfläche und sich über der Wasseroberfläche befindlicher Inseloberfläche.
Die unter der Wasseroberfläche versunkene Fläche lässt sich abschließend berechnen, indem der kubische Spline betrachtet wird, welcher von der horizontalen Ebene geschnitten wird. Die Schnittstelle gibt in diesem Fall einen Punkt an, dessen y-Koordinate als neue Obergrenze für das Spline-Funktions-Integral verwendet werden kann.
Ebenso gibt die x-Koordinate der Schnittstelle den Punkt des Gesamtradiusses an, welcher anteilig verloren geht.
Somit kann sowohl die verlorengegangene Oberfläche als auch die Grundfläche der Insel berechnet werden.
Das Modell soll also am Ende über die Möglichkeit verfügen bei beliebiger Jahreszahl mit damit verbundenem SLE die korrespondierenden Grund- und Oberflächenverluste der Insel Bornholm anzugeben.
In Abbildung 29 wurden die oben genannten Kreisflächen berechnet. Dabei wurde bei dem größten Höhenniveau begonnen und anschließend sukzessive bis zum geringsten Höhenniveau vorgegangen.
Die Rechnung basiert auf folgender Vorgehensweise:
Hier wurde zunächst der aktuelle Gesamtradius aller bereits bestehenden Kreisscheiben berechnet, sodass "A0" die Fläche aller voriger Kreisscheiben bezeichnet und "A1" den Flächenbeitrag der aktuellen Kreisscheibe.
Beim ersten Rechendurchgang liefert dies genau den Radius der ersten Kreisscheibe, an den nun immer mehr Kreisringe dazu addiert werden und ihre jeweiligen Beiträge zum Gesamtradius.
Im Anschluss wird der Radius ("r1-2") von Scheibe 1 bis Scheibe 2 berechnet, indem man zur Flächensumme der bisherigen Scheiben ("A0-1") die Fläche der aktuellen Scheibe (A2) dazu addiert.
Beim zweiten Rechendurchgang bekommt man also einen neuen "Gesamtradius" für die ersten beiden Kreisscheiben.
Bildet man nun die Differenz der beiden Radien, so erhält man den Beitrag zum bisherigen Gesamtradius, welcher die zweite Scheibe (bzw. der erste Ring) leistet:
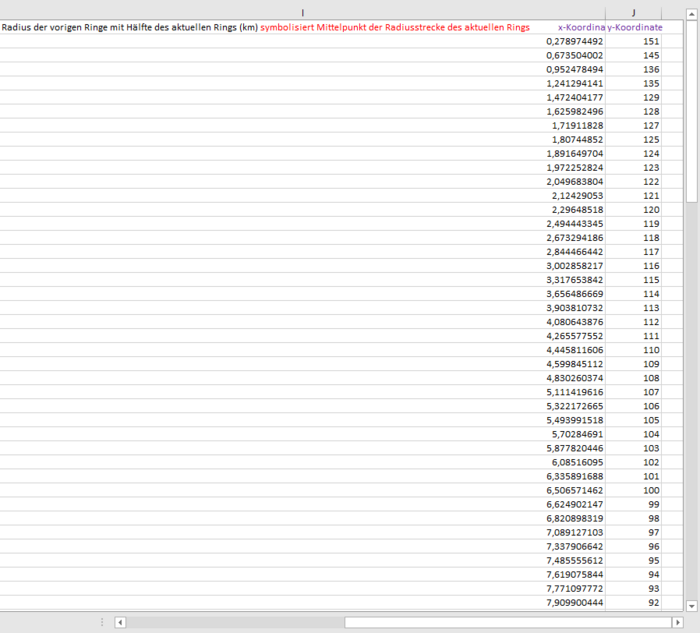
Diese Methode wird für alle Höhenniveaus durchgeführt. Anschließend werden die Mittelpunkte der jeweiligen Radienstrecken berechnet, indem man zum vorigen Gesamtradius immer die Hälfte des aktuellen Radius dazuaddiert.
Die Damit berechneten Mittelpunkte, dienen als x-Koordinaten für unsere Spline-Knotenpunkte, wohingegen die Höhenniveaus (Höhenmeter) die y-Koordinaten bilden.
In Abbildung 29 ist die oben beschriebene Rechnung mit ihren Ergebnissen als Ausschnitt abgebildet, da auch hier die Datei mehr als 100 Zeilen lang ist. In Abbildung 30 sind die damit berechneten Koordinaten unserer Spline-Knotenpunkte ausschnittssweise abgebildet.

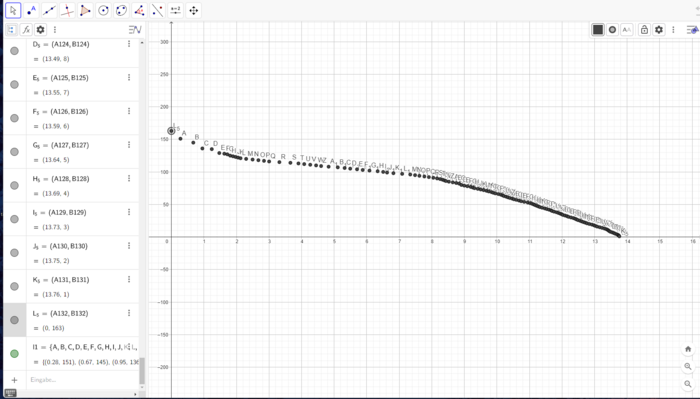
In Abbildung 31 können die berechneten Spline-Knotenpunkte in GeoGebra betrachtet werden.
Ursprünglich war angedacht eine Visualisierung des Rotationskörpers nach Eingabe der über 100 kubischen Spline-Funktionen zu realisieren. Durch die enorme Datenmenge kommt GeoGebra hier an seine Grenzen und kann dementsprechend nicht zur Realisierung der beabsichtigten Visualisierung herangezogen werden. Eine Realisierung mit Octave kommt aus Gründen des Zeitmangels nicht mehr in Frage, weshalb wir fortan auf eine akkurate Visualisierung verzichten müssen und diese nur anhand einer beliebig generierten Funktion andeuten werden. Diese soll nur das theoretisch mögliche Ergebnis zeigen, welche Aufgrund der limitierten Rechenleistung von GeoGebra (bzw. unseren Computern) nicht umsetzbar ist.
Die damit verbundenen Rechnungen kann GeoGebra für sehr einfach zu berechnende Integrale übernehmen, da wxMaxima als Computeralgebra-Programm aber schneller und effizienter arbeitet, wird fortan mit wxMaxima weitergearbeitet, da sich Visualisierung und Rechnung nicht in einer GeoGebra-Datei realisieren lassen und somit nur der algebraische Teil übrig bleibt. (s.o.).
Zur Berechnung der kubischen Splines wird ein externer Spline-Rechner verwendet. [10]
Mithilfe dieses Rechners wurden zunächst Kubische Splines berechnet, welche in Bruch und Dezimalzahldarstellung angegeben werden können.
In Abbildung 32 ist der Rechner zu sehen, welche unsere Punkte dazu verwendet, um die kubischen Splines zu berechnen. Diese sind in diesem Fall zunächst nur schlecht im Graphen zu sehen und lassen sich leider auch nicht anders darstellen. Dazu ist der Rechner nicht in der Lage, weswegen wir im nächsten Schritt zu Verdeutlichung unserer Herangehensweise eine weitere Betrachtung von weniger Splines vornehmen.

Abbildung 33 zeigt probeweise nur die Splines für die ersten vier Spline-Knotenpunkte. Angedacht ist es, mit den einzelnen Splinefunktionen in Kombination mit den prognostizierten Höhenwerten einen Punkt auf der Splinefunktion im jeweiligen Bereich zwischen zwei Knoten zu finden, sodass man entweder über Integralrechnung den Verlust der Oberfläche der Insel über Berechnung der Mantelfläche des Rotationskörpers ermitteln kann oder alternativ über Berechnung der x-Koordinate den Verlust der Inselgrundfläche, indem man den neuen Gesamtradius der Insel berechnet und daraus den Verlust an Grundfläche folgert.
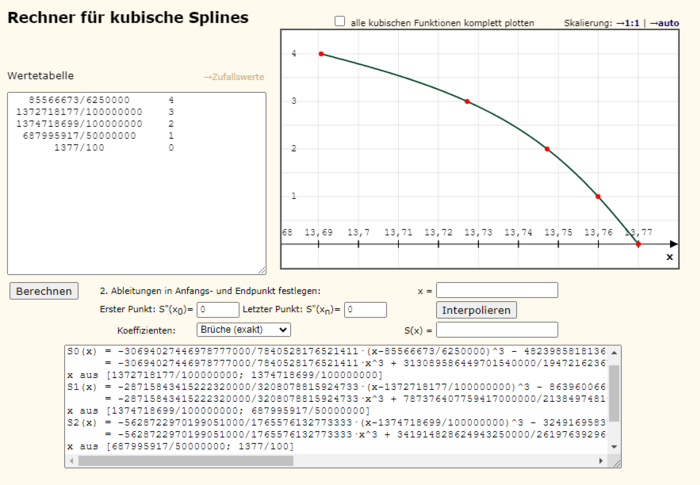
Da der Rechner die berechneten Splines auf unterschiedlichste Art Darstellen kann, wäre die genauste Variante, eine Bruchdarstellung, wie sie unten in Abbildung 34 zu sehen ist.

Alternativ kann der Rechner die Darstellung auf eine gewünschte Anzahl Dezimalstellen runden, was natürlich mit Rundungsfehlern verbunden ist. Ein Ausschnitt der Liste ist in Abbildung 35 zu sehen. Hier wurde auf zwei Dezimalstellen nach dem Komma gerundet.

Um die Überschwemmung der Insel und den damit verbundenen Flächenverlust zu berechnen, muss mit dem Höhenniveau zwischen NN und 1m begonnen werden, was aufgrund unseres Datensatz dem 131. Spline entspricht. Dia Eingabe in wxMaxima wird in Abbildung 36 gezeigt. Man sieht in gelb die von wxMaxima vorgenommenen Umänderungen, welche nicht zu umgehen waren. Diese scheinen aber keinen Einfluss auf das Ergebnis zu haben.

Wie in Abbildung 37 zu sehen ist, gibt es generelle Schwierigkeiten mit wxMAxima, sobald es darum geht extrem große Dimensionen von Zahlen und Ausdrücken darzustellen oder zu vereinfachen. Woran genau dies liegt und ob einfach ein Fehler programm-syntaktischer Natur vorliegt, kann von unserer Gruppe nicht näher herausgefunden werden und wir konnten leider keine Lösung dieses Problems finden, sodass leider keine konkrete Zahl als Ergebnis ausgegeben werden kann.
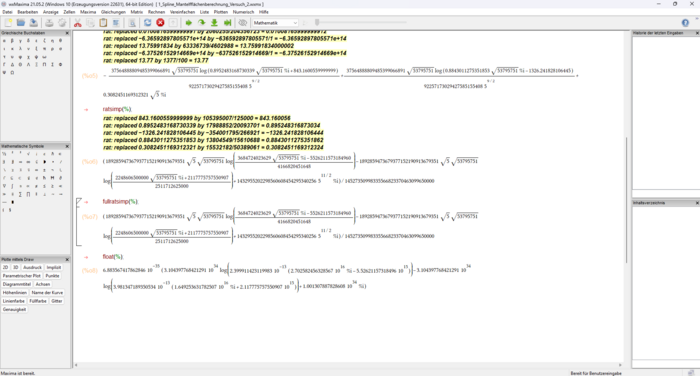
Um dem Problem etwas entgegenzuwirken, haben wir uns dazu entschlossen, die Zahlen probeweise als gerundete Variante (auf zwei Dezimalstellen gerundet) von wxMAxima verarbeiten zu lassen, was zumindest ein konkretes Zahlergebnis ausgibt. Dieses ist unten rechts in Abbildung 38 zu sehen. Wie sich aber zeigen wird, ist eine derartig starke Rundung der Zahlenwerte mit einem großen Fehler verbunden, welcher so große Dimension annimmt, dass die erhaltene Lösung gänzlich unbrauchbar wird. Dies wird im späteren Vergleich in GeoGebra weiter ausgeführt.
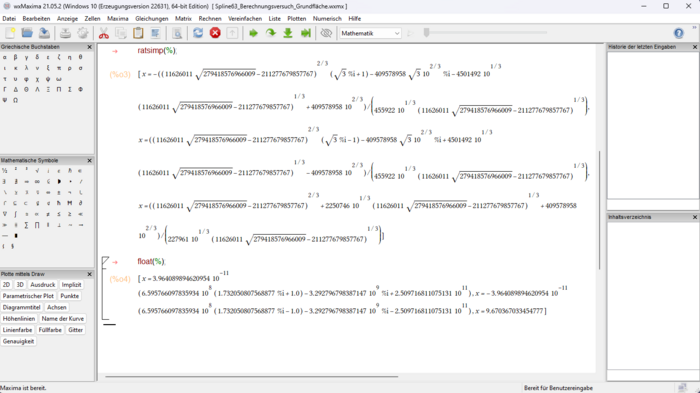
Um die Misserfolge von diesem Teil der Modellierung einigermaßen aufzufangen, sind wir von kubischen Splines auf eine simplere Methode umgestiegen, welche aus zeitlichen Gründen nicht mehr so detailliert und vollständig durchgeführt wird. Die Vorgehensweise wird geometrisch mithilfe von GeoGebra für ein einziges konkretes Beispiel gezeigt und anschließend beschrieben, wie dies fortführend für beliebe Werte verwendet werden kann, um als alternative für die Methode mit kubischen Splines zu fungieren.
Im Wesentlichen sind wir von kubischen Splinefunktionen auf lineare Funktionen umgestiegen, um letztlich Zahlendimensionen zu erhalten, welche zumindest leichter mit Computer-Algebra-Systemen gelöst werden könnten.
Um dies kurz zu beschreiben, wie dies mit linearen Funktionen zu realisieren ist, schauen wir uns Abbildung 39 an. Hier ist ein Ausschnitt aus GeoGebra zu sehen, welcher im Wesentlichen alle ehemaligen Spline-Knotenpunkte beinhaltet, welche nun zu Knotenpunkten von linearen Funktionen verwendet werden sollen. Geometrisch kann man durch Streckenbildung zwischen zwei Punkten diese linearen Funktionen geometrisch bestimmen, statt sie auszurechnen (was alternativ genauer ist). Da es durch zwei Punkte stets genau eine lineare Funktion gibt, können die einzelnen linearen Funktionen somit alle aus den ehemaligen Spline-Knotenpunkten berechnet werden. Aus Zeitgründen wird hier nur anhand eines Beispiels eine x-Koordinate bestimmt, um den Verlust der Grundfläche Bornholms einmal für das gesamte Abschmelzen der Eismassen zu zeigen.
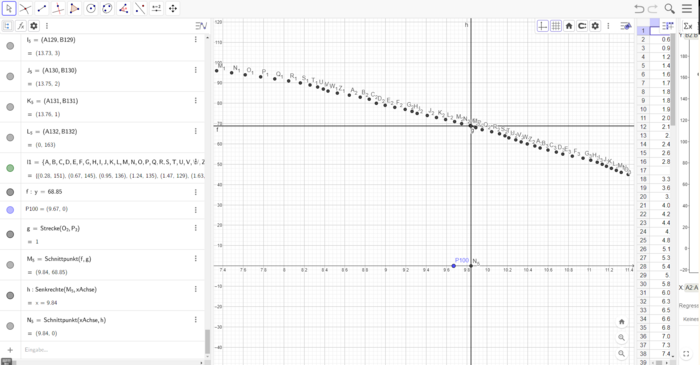
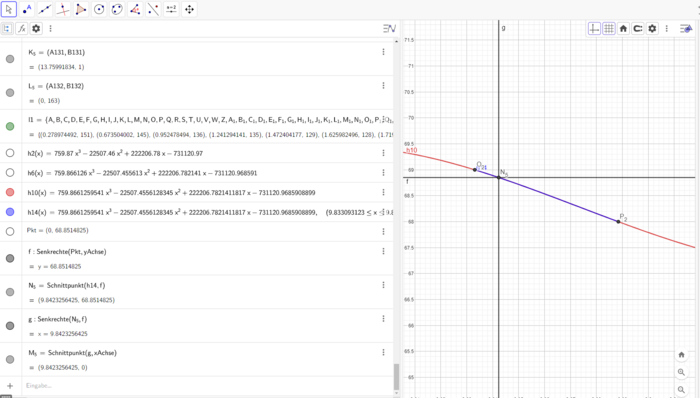
Abbildung 40 zeigt eine vergrößerte Szene von dem in Abbildung 39 gezeigten Punktemenge. Hier wurde durch verbinden der beiden Punkte die lineare Funktion simuliert, welche durch diese beiden Punkte verlaufen würde. Die Parallele zur x-Achse wird durch unseren Höhenwert bestimmt, welcher aus unserer Prognosedatei stammt (vgl. Abbildung 18). Dabei wurde eine Erhöhung des Meeresspiegels um umgerechnet 68851,4825 Millimeter oder gerundet 68,852 Meter prognostiziert, sollte das gesamte Eis abschmelzen. Damit wird nun die lineare Funktion geschnitten, was den Punkt M5 liefert. An und für sich hat man nach Erhalt dieses Punktes Koordinaten für den Punkt gegeben, allerdings gibt GeoGebra diese Koordinaten nur bis auf zwei Dezimalstellen gerundet an, was in diesem Fall nicht genügt. Daher wird ein Lot auf die x-Achse gefällt und anschließend sehr nah an den Punkt und damit die x-Achsenbeschriftung gezoomt, was uns mehr Nachkommastellen liefert. Die nun ablesbare x-Koordinate liegt nun zwischen 9,841286 und 9,841287. Wir haben diese Zahl mit Augenmaß auf 9,8412863 interpoliert, was natürlich im Optimalfall genauer berechnet werden sollte. Dies ist aufgrund der mangelnden Zeit und dem unerwarteten oben genannten Fehlschlag ein willkommener Kompromiss den wir eingegangen sind. In Abbildung 41 ist der herangezoomte Ausschnitt zur Nachvollziehbarkeit noch einmal abgebildet.


In Abbildung 42 ist die Berechnung der verlorenen Grundfläche und des Radius zu sehen. Sollten im schlimmsten Fall alle Massen komplett abschmelzen, so würde Bornholm von seinen aktuellen 594,81 Quadratkilometern etwa 290,55 Quadratkilometer Grundfläche verlieren, was prozentual etwa 48,85% beträgt.

Nachtrag zu den kubischen Splines: Nach einigen Versuchen, ist es uns mithilfe von GeoGebra gelungen, zumindest eine geometrische Lösung analog zu der oben beschriebenen Lösung mithilfe linearer Funktionen zu erhalten. Die Lösung wird hier nur in Form eines Koordinatenpunktes angegeben. Die Rechnungen können analog wie bei den linearen Funktionen durchgeführt werden. Die Abbildung 42 wurde aktualisiert und enthält zum Vergleich beide Lösungen.
Ergebnisse
[Bearbeiten]In diesem Bereich werden alle Ergebnisse, welche durch die einzelnen Modellierungszyklen entstanden sind kurz und prägnant miteinander verglichen und diskutiert:
Beginnen wir mit den Prognosefunktionen der einzelnen Zyklen so kann schnell gesagt werden, dass die Funktionen mit fortschreitendem Zyklus immer eine größer werdende schmelzende Eismasse prognostizieren. Die Funktionen der ersten beiden Zyklen berücksichtigen nur die bereits gemessenen Werte und bauen auf diesen mathematisch auf. Die Potenzfunktion aus Zyklus 3 dahingegen berücksichtig unter einem vermuteten proportionalen Zusammenhang zwischen anthropogener Erderwärmung und Eisschmelze. Dies ist zwar prinzipiell sinnvoll, aber es handelt sich generell um einen sehr komplexen Zusammenhang, wenn es um das Schmelzverhalten der Eismassen im globalen Sinn geht.

Generell muss gesagt werden, dass es regionale Faktoren gibt (bspw. Winde, Durchschnittstemperaturen, Wasserströmungen, etc.) welche die Komplexität des hier zugrunde gelegten Sachverhalts derart sprengen würden, dass die Problematik analytisch kaum zu beschreiben wäre. Wir haben hier einige Vereinfachungen vorgenommen. Wir haben alle Eismassen mit dem gleichen Abschmelzverhalten abschmelzen lassen und ebenso sehr viele Faktoren (vgl. oben)nicht berücksichtigt, da es weder verträgliche Daten, noch analytische Ansätze gibt, diese sinnvoll mathematisch zu beschreiben. Dementsprechend, haben wir uns hier auf simple Überlegungen gestützt und versucht eine Dimension zu schaffen, in welcher sich ebensolche Faktoren bei einem vermuteten Zusammenhang ausdrücken lassen.
Fortführend schauen wir uns einmal die Abschmelzjahreszahlen der einzelnen Zyklen im Vergleich an:
| Eisregion | Zyklus 1: 5-Jahresintervall (Jahr+4) | Zyklus 2: 5-Jahresintervall (Jahr+4) | Zyklus 3: Jahreszahl |
|---|---|---|---|
| Gletscher | 2057 | 2057 | 2057 |
| Eiskappen | 2067 | 2067 | 2065 |
| Grönland Eisschild | 2422 | 2412 | 2355 |
| Antarktis Eisschild | 3292 | 3267 | 3018 |
| Alle | 3367 | 3342 | 3074 |
In Tabelle 8 sind alle drei Zyklen miteinander abgebildet. Man erkennt, dass es bei den ersten beiden Zyklen nur wenige Unterschiede gibt, so besteht beispielsweise bei Gletscher und Eiskappen gar kein Unterschied und erst im dritten Zyklus wird bei der Menge entsprechend der Eiskappen eine schnellere Schmelze prognostiziert. Dies ergibt auch Sinn, da die ursprünglichen Funktionen anfangs sehr nah beieinander liegen und erst im späteren Verlauf markant unterschiedlichere Werte prognostiziert. Dies wird im Verlauf der Schmelze deutlich. So wird ab einer Schmelze, welcher der Masse des Grönlandeisschilds entspricht, Änderungen in der Prognose von 10 bis 57 Jahre Unterschied prognostiziert. Mit zunehmender geschmolzener Eismasse wird die Prognose also immer schneller, sodass bei der größten Eismasse, etwa bei der Antarktis und damit verbunden auch in der Gesamtmasse, die größten Prognoseunterschiede zu sehen sind.
Damit verbunden ist auch ein von uns in Zyklus 3 berechnetes SLE von etwa 68,852 m, sollte die gesamte Eismasse der Erde abschmelzen.
Wie in Zyklus 2 schon thematisiert, würde dies für Deutschland eine Betroffenheit von mindestens 28,52% der Landmasse im Norden Deutschlands bedeuten und konkret laut Zyklus 3 für die Insel Bornholm in Dänemark einen Flächenverlust von gerundet 48,85% der Landmasse bedeuten.
Laut unserer Recherche leben auf Bornholm durchschnittlich 77 Einwohner pro Quadratkilometer [11]. Betrachtet man nun den Flächenverlust, so würde dies bedeuten, dass laut dem Durchschnittswert etwa 22.373 Einwohner (lineare Funktion: aufgerundet von 22.372,35) bzw. 22.368 (kubische Splines: aufgerundet von 22.367,16) ihren Lebensraum verlieren würden und dementsprechend umgesiedelt werden müssten.
(Alle Dateien und Ergebnisse sind unter folgendem Drop-Box-Link abrufbar: (folgt))
Optimierung des Modells
[Bearbeiten]Da unser Modell wie in den Ergebnissen beschrieben sehr viele Faktoren nicht analytisch fassen kann und damit auch nicht mathematisch berücksichtigen kann ohne erheblich mehr Zeit und Kosten aufbringen zu müssen (was im Rahmen der Veranstaltung nicht umzusetzen wäre, da es internationaler Koryphäen bedarf, diese Sachverhalte zu interpretieren und zu mathematisieren und in erster Linie Daten vor Ort zu erheben). Dementsprechend wäre eine Optimierung natürlich noch mehrere Faktoren in die Modellbildung mit aufzunehmen. Einige Faktoren, welche generell berücksichtigt werden müssten, werden nachfolgend genannt:
- Strahlungsmenge und Bestrahlungszeit
- Ozeantemperatur
- atmosphärische Zirkulationsmuster
- Albedo
- topografiespezifische Absorption und Reflektion
- Niederschlagsmuster und Niederschlagsmengen
Um diese Faktoren berücksichtigen zu können, müssten langjährige Messungen vor Ort durchgeführt werden. Dazu fehlt uns sowohl die Kompetenz, als auch Zeit und Geld. Daher musste darauf verzichtet werden.
Ebenso kann das Modell optimiert werden, indem die verwendeten Programme erweitert werden. Gerade in Zyklus 3 mussten wir auf eine Insel zurückgreifen, welche keine Täler beinhaltet, da wir diese nicht adäquat hätten berücksichtigen können. Wir hätten ein weitaus komplizierteres Modell aufspannen müssen, was mit den uns zur Verfügung stehenden Mitteln nicht ohne einen enormen zeitlichen Mehraufwand möglich gewesen wäre. Daraus kann man aber in sich ein eigenes Modell aufbauen und das tatsächliche Relief nachmodellieren. Prinzipiell hätte man es mit einer Software namens AutoCAD schaffen können, welche von Bauingenieuren dazu verwendet wird, ebensolche Probleme zu lösen. Da dies aber mit einem Preis von über 2000€/Jahr verbunden wäre und dementsprechend auch eine gewisse Expertise voraussetzt, welche wir ebenfalls erst hätten erreichen müssen, ist dies außer Frage.
Gerade mit den von uns benutzten Programmen GeoGebra und wxMaxima sind wir schnell an gewisse Grenzen gestoßen, sobald die Zahlendimension zu groß bzw. zu klein wurde. Dabei entstanden Rundungsfehler und so starke Abweichungen, dass keine verwertbaren Ergebnisse dabei entstanden wären. Mit Blick in die Zukunft kann aber versucht werden, diese Problematik mit anderen Programmen etwa R-Studio oder GNU Octave zu umgehen. Dies zu testen lag leider nicht mehr im Bereich des Möglichen, da die Probleme erst am Ende des Modellierens klar wurden und aufgrund mangelnder Zeit nicht mehr adäquat darauf reagiert werden konnte, weswegen notgedrungen ein anderer Weg eingeschlagen werden musste. Prinzipiell kann man aber sagen, dass GeoGebra rechenleistungstechnisch nicht mit 131 Spline-Funktionen hantieren kann. GeoGebra stürzt auf unseren Computern nach 5 solcher Funktionen bereits beim Reinzoomen ab. Von einer Umsetzung und Visualisierung mit GeoGebra musste dementsprechend komplett abgesehen werden. wxMaxima hingegen hat ab einem gewissen Rechenaufwand Probleme damit die Ausdrücke konkret auszurechnen bzw. darzustellen. Hier bleibt allerdings zu klären ob die Problematik dem Programm selbst geschuldet ist oder auf syntaktische Eingabefehler unsererseits zurückzuführen sind. Dies konnte von uns leider nicht festgestellt werden.
Daher sind wir von kubischen Splines auf lineare Funktionen umgestiegen und mit mehr Zeit hätte man das gesamte Modell daran anpassen und für alle Knotenpunkte die zugehörige lineare Funktion bestimmen können. Ebenso wäre es möglich gewesen mit mehr Zeit und ein paar Kenntnissen in Python eine GUI zu erstellen, welche nach Eingabe einer Jahreszahl oder eines beliebigen Anstiegs des Meeresspiegels den dazugehörigen Flächenverlust für Bornholm ausgibt.
In Abbildung 44 ist die Art der Visualisierung zu sehen, wie sie für die erstellte Insel ursprünglich angedacht war. Prinzipiell wäre eine solche Visualisierung für weniger komplex zu beschreibende Rotationskörper möglich gewesen. Wir zeigen die Visualisierung, um unsere Gedankengänge und Vorgehensweisen nachvollziehbarer zu gestalten. Es wäre eine schöne Möglichkeit gewesen, den graduellen Anstieg des Meeresspiegels anhand unserer selbst modellierten Insel zu begutachten. Leider mussten wir darauf verzichten.
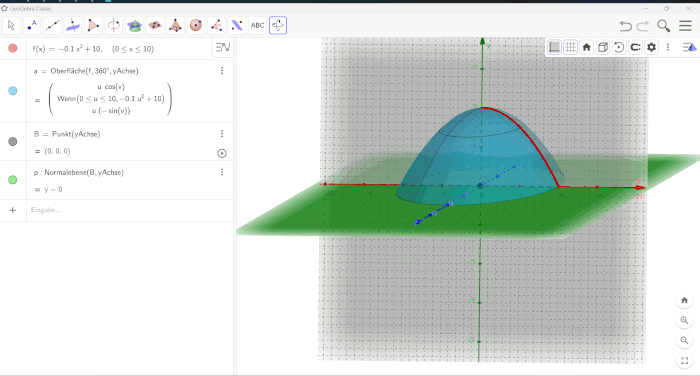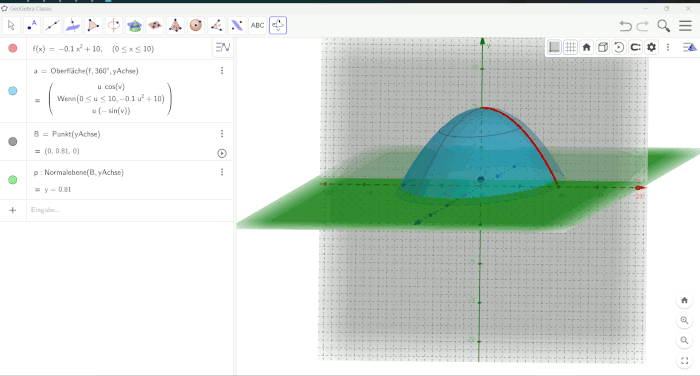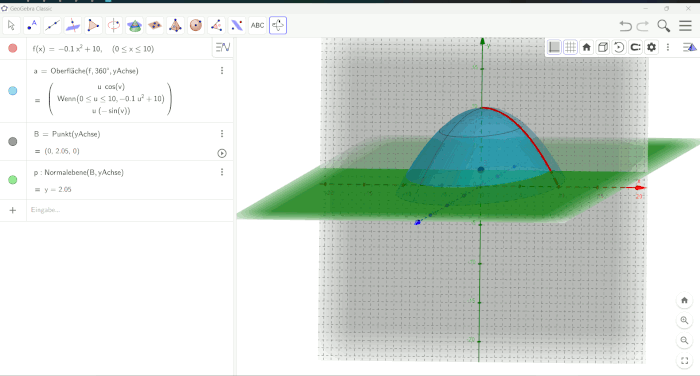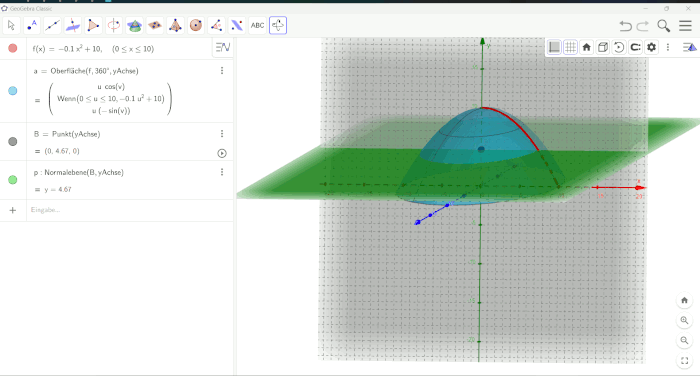
Mit diesen Überlegungen schließen wir die Optimierungsgedanken und -möglichkeiten ab.
Zusammenfassung
[Bearbeiten]Betrachtet man unser Modell und unseren Modellierungsweg, so kann man zusammenfassend sagen, dass wir uns zu Beginn mehr auf die Modellierung der Eismassen konzentrierten und im Nachgang an einem konkreten Beispiel einen Verlauf generieren wollten, der es dem Leser ermöglicht eine von ihm gewählte Jahreszahl oder SLE-Wert in einen Flächenverlust umzurechnen.
Dies hat generell zwar nicht reibungslos funktioniert, aber generell kann gesagt werden, dass wir anhand eines Rechenbeispiels gezeigt haben, dass unser Modell dazu in der Lage ist, mit etwas mehr Zeit den Grundflächenverlust Bornholms, mit den eben beschriebenen Werten, lückenlos zu füllen. Daher kann nach der in Zyklus 3 zuletzt verwendeten Methodik für jeden SLE-Wert (oder Jahreswert) die dazugehörig verlorene Fläche Bornholms ermittelt werden.
Andererseits konnten wir leider keinen Rotationskörper der Insel erstellen und auch nicht den Oberflächenverlust über eine durch Integralrechnung berechnete Mantelfläche darstellen. Dies wäre didaktisch schön gewesen, da man dies besser interpretieren kann, da die Insel Bornholm leider kein absolutes Flachland ist, sondern Relief besitzt. Somit konnten wir lediglich den Verlust an Fläche beschreiben, welcher verloren geht, wenn sich die Strandlinie verschiebt und die damit verlorene Grundfläche.
Tutorium
[Bearbeiten]Diese Rubrik dient nur zum schnelleren Erreichen der Tutoriumsseite: https://de.wikiversity.org/wiki/Kurs:Mathematische_Modellbildung/Themen/2023-24_Wintersemester/Tutoriumsseite_Modellbildung
Literatur
[Bearbeiten]- ↑ Climate Change 2001: Working Group I: The Bcientific Basis: Changes In Sea Levels. Chapter 11, Table 11.3 - https://web.archive.org/web/20071216235037/http://www.grida.no/climate/ipcc_tar/wg1/412.htm#tab113 (Zuletzt abgerufen am 28.11.2023)
- ↑ Bamber et al. 2016: The land ice contribution to sea level during the satellite era. Environmental Research Letters, Volume 13. Number 6. p. 14 - https://iopscience.iop.org/article/10.1088/1748-9326/aac2f0/pdf (Zuletzt abgerufen am 12.12.2023)
- ↑ Royal Holloway University of London: Calculating glacier ice volumes and sea level equivalents. London 2023, S. 5 - https://www.antarcticglaciers.org/glaciers-and-climate/estimating-glacier-contribution-to-sea-level-rise/ (Zuletzt abgerufen am 24.01.2024)
- ↑ https://commons.wikimedia.org/wiki/File:Fm_stirling_pool.jpg#globalusage
- ↑ Bundesministerium für Wohnen, Stadtentwicklung und Bauwesen, Referat S III 1 - Grundsatzangelegenheiten Raumordnung. Deutschlandatlas - https://www.deutschlandatlas.bund.de/DE/Karten/Wo-wir-leben/006-Bevoelkerungsdichte.html (Zuletzt abgerufen am 30.01.2024)
- ↑ Environmental Change Institute of Oxford University: Tracking Progress to Save Climate - https://www.globalwarmingindex.org/ (Zuletzt abgerufen am 24.01.2024)
- ↑ Calculating glacier ice volumes and sea level equivalents - https://www.antarcticglaciers.org/glaciers-and-climate/estimating-glacier-contribution-to-sea-level-rise/ (Zuletzt abgerufen am 28.11.2023)
- ↑ TessaDEM Datenbank - https://de-de.topographic-map.com/map-4lbzs/Bornholm/ (Zuletzt abgerufen am 28.11.2023)
- ↑ Ferien Bornholm - The official Guide: Fakten über Bornholm -https://bornholm.info/de/fakta-om-bornholm/#:~:text=Die%20Insel%20in%20Zahlen,K%C3%BCstenstrecke%3A%20158%20km. (Zuletzt abgerufen am 24,01,2024)
- ↑ Arndt Bruenner: Kubische Splines - https://www.arndt-bruenner.de/mathe/scripts/kubspline.htm (Zuletzt abgerufen am 24.02.2024)
- ↑ Ferien Bornholm - The official Guide: Fakten über Bornholm -https://bornholm.info/de/fakta-om-bornholm/#:~:text=Die%20Insel%20in%20Zahlen,K%C3%BCstenstrecke%3A%20158%20km. (Zuletzt abgerufen am 24,01,2024)







![{\displaystyle 26.345.958km^{3}*1.000.000.000*1.000=26.345.958.000.000.000m^{3}*1.000=26.345.958.000.000.000.000dm^{3}[Liter]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97b92fc6d5ec9dd7316552fbd37ef835903783a0)

![{\displaystyle 2.000m^{3}*1.000=2.000.000dm^{3}[Liter]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b015c3a243a46565b51713ac51c32707837441b5)





