Kurs:Mathematische Modellbildung/Themen/2023-24 Wintersemester/ Spagat im Alltag und im Tanzverein

Spagat Modellierung

zurück zur Übersichtsseite WS 23-24

Gruppenteilnehmer

1. Aaron Weiß
2. Lorenz Pietsch
3. Melina Eitz

Zielsetzung des Modellierungsthemas

Die hauptsächliche Zielsetzung dieses Projektes ist das Finden von Merkmalen die mit der Tiefe eines Spagats korrelieren, sowie einige Vorhersagen zu treffen und die lineare und multiple Regression zu untersuchen. Die Tiefe eines Spagats ist definiert als die Länge der Senkrechte zwischen Leiste des Probanden zum ebenen Boden. Auf diesen Korrelationsmerkmalen aufbauend war ein weiteres Ziel des Projektes, das Erstellen einer Zeit-Prognose für eine Person die einen Spagat erlernen möchte. Also, wie lange benötigt eine individuelle Person, um mit einem bestimmten Trainingsprogramm einen vollständigen Spagat zu erlernen. Außerdem war geplant, die Korrelationsmerkmale in einem längen Zeitraum zu betrachten. Im Laufe der Projektarbeit haben sich weitere Nebenfragen entwickelt welche mit diesem Projekt verwandt sind:

• Sind Menschen die einen Spagat können weniger anfällig für Hüftgelenksimplantationen?
• Sind Menschen die einen Spagat können weniger anfällig für Lower Back Pain?

Aufgrund mangelnder Zeit und mangelnder Partizipation freiwilliger Probandinnen und Probanden, hat sich die Gruppe entschlossen sowohl die Zeitprognose, die Untersuchung der Merkmale über einen längeren Zeitraum, als auch die Nebenfragen nicht zu bearbeiten. Das Projekt handelt zum Zeitraum des Wintersemesters 2023/24 nur von möglichen Korrelationen und der linearen, sowie multiplen Regression zur Spagattiefe.

Motivation für das Thema

Warum das Modellierungsthema Spagat? Aufgrund dessen, dass eine Studentin aus unserer Gruppe in einem Karnevalsverein aktiv ist, in dem regelmäßig Spagat vom Alter von drei bis dreißig Jahren trainiert wird, hat sie sich gefragt wie man am effektivsten Spagat lernen kann. Da der Rest der Gruppe sportinteressiert und sportbegeistert ist, wurde der Vorschlag angenommen, da wir alle die Tanzfigur selbst erlernen wollten.

Während des Modellierprozesses haben wir entdeckt, dass das Thema auch für die Gesundheit relevant sein könnte. Zum einen kann ein Spagattraining die Beweglichkeit und das eigene Körpergefühl verbessern und zum anderen die Flexibilität in der Hüfte steigern. Außerdem haben wir uns gefragt ob durch das Spagattraining, das Einsetzen von künstlichen Hüftgelenken reduzieren würde. Besonders interessiert hat uns, welche körperlichen oder alltäglichen Faktoren eine positive Auswirkung für einen tieferen Spagat haben. Auf den letzten Punkt haben wir uns in diesem Modellierungsthema fokussiert.

Definition: Spagat

Bei einem Spagat handelt es sich um eine Figur aus dem Tanz- oder Gymnastikbereich, bei der die Beine einer Person bis zum maximalen Winkel (0-180 Grad), in einer geraden Linie gespreizt werden.

Man unterscheidet zwischen zwei verschiedene Spagattypen:

Beim Seitspagat, besser bekannt als Männerspagat, werden die Beine seitlich vom Körper gespreizt, während beim Querspagat, auch Frauenspagat genannt, ein Bein nach vorne und das andere nach hinten vom Körper weggespreizt wird. Hier wird ebenfalls zwischen Rechten und Linken Frauenspagat unterschieden. Der Spagat wird nach dem Bein benannt, das nach vorne gestreckt wird. Unabhängig von der Bezeichnung können Frauen sowie Männer beide Spagatfiguren gleichermaßen erlernen. Die Begriffe Männer- und Frauenspagat wurden nicht wegen biologischen Unterschieden festgelegt, sondern durch die Vorstellungen, dass einem Mann einen Seitspagat aufgrund seiner körperlichen Struktur besser gefallen könnte.

Zuordnung des Modellierungsthemas zu den UN-Nachhaltigkeitszielen [1]

Im Rahmen des Kurses "Mathematische Modellbildung" beabsichtigen wir als Gruppe, aktiv am Prozess der nachhaltigen Entwicklung teilzunehmen. Wir werden uns dabei an den Zielen der nachhaltigen Entwicklung orientieren, wie sie in der UN-Agenda "Transformation unserer Welt: die Agenda 2030 für nachhaltige Entwicklung" festgelegt sind, und diese Ziele unserem mathematischen Modell zuordnen.

• SDG 3 (Good Health and Well-being):

Spagattraining verbessert die Flexibilität und Mobilität des Körpers, was zu einem besseren körperlichen Wohlbefinden und auch zu einer besseren Gesundheit beitragen kann. Insbesondere die Beweglichkeit im Hüftgelenk wird durch Spagattraining verbessert aber auch die Beweglichkeit in der Lendenwirbesläule ist relevant.

Gesundheitliche Aspekte und mögliche Korrelationen

"Die Anzahl der Implantationen künstlicher Hüftgelenke in Deutschland im Jahr 2021, betrug 300,8 je 100.000 Einwohner."[vgl. [2]] Übertragen auf die "gesamte deutsche Bevölkerung von 83,24 Mio im Jahr 2021."[vgl.[3]] waren das 250.385,92 Implantationen im Jahr 2021. Ein adäquates Mobilitätstraining kann eine präventive Maßnahme dagegen sein und ein Spagattraining ist unter gewissen Bedingungen eine angebrachte Wahl. Der Front-Split beinhaltet zum Beispiel Bewegungen in fast alle Bewegungsrichtungen des Hüftgelenks: Hüft -Flexion, -Extension, -Abduktion und -Innenrotation, und fördert somit die Beweglichkeit in die genannten Richtungen. Ebenso wird die Beweglichkeit in der Lendenwirbelsäule positiv durch Spagattraining beeinflusst. In korrekter Ausführung ist die Flexion in der Lendenwirbelsäule notwendig. Denn ohne eine Flexion in der Lendenwirbelsäule steht die Anatomie des Beckens, insbesondere die Anatomie des Hüftgelenks einem vollen Spagat im Weg. Somit lässt sich eine Korrelation vermuten, die besagt, dass Menschen die einen vollständigen Männerspagat ausführen können weniger unter dem LWS-Syndrom, auch Lower Back Pain genannt, leiden.

• SDG 4 (Quality Education):

Die Förderung von Sportaktivitäten wie Spagattraining in Schulen und Gemeinschaften kann dazu beitragen, das Bewusstsein für körperliche Gesundheit zu schärfen und den Schülerinnen und Schülern eine ganzheitliche Bildung zu bieten.

• SDG 5 (Gender Equality):

Spagattraining verbessert das eigene Körpergefühl und kann dabei auch helfen die Grenzen des eigenen Körpers zu erkunden. Biologische Unterschiede zwischen den Körpern eines Mannes und einer Frau werden nachvollziehbar und Geschlechtsstereotypen können besser durchbrochen werden.

Niveauzuordnung

Niveau Sek. I

• Erstellen eines Umfragebogens und eines Messblatts zur Datenerhebung bezüglich möglicher Merkmale die mit der Spagattiefe korrelieren könnten [Microsoft Word]

• Durchführen der Umfrage und der Messungen mit verschiedenen Probanden

• Erste Datenanalyse (Box Plot, arithmetisches Mittel) [Microsoft Word, Microsoft Excel]

Niveau Sek. II

• Untersuchung der Daten auf Messabweichungen [Microsoft Excel]

• Darstellung verschiedener Korrelationen durch Diagramme [Microsoft Excel, R-Studio]

• Lineare Regression [Microsoft Excel]

Niveau Universität

• Multiple lineare Regression [R-Studio, Maxima]
• Darstellung der multiplen linearen Regression mit Regressionsebenen [R-Studio, Maxima]

Modellierungszyklen

Stufe Sek I / Zyklus I

Aufgrund der unzureichenden Datenlage bezüglich der Zielsetzung, musste die Gruppe selbstständig die notwendigen Daten erheben. Die Arbeitsprozesse, um wissenschaftlich Daten zu erheben, sind im engeren Sinne kein Bestandteil mathematischer Modellbildung, denn zum Erheben von Daten sind keine mathematischen Kenntnisse oder Fähigkeiten notwendig, sodass man diesen Teil auslagern könnte. Im weiteren Sinne ist die Datenerhebung ein Bestandteil mathematischer Modellbildung. Geeignete Daten sind zwingend notwendig um Statistik zu betreiben, welches das mathematische Kerngebiet in der Modellbildung dieses Projektes ist. Aus diesem Grund aber auch weil das Erheben von Daten zu den Kernkompetenzen wissenschaftlichen Arbeitens zählt, werden die konkreten Arbeitsphasen zur Datenerhebung mit in den ersten Zyklus aufgenommen. Denn dies kann durchaus auch Bestandteil des Unterrichts der Sekundarstufe I sein. Hierbei können Schüler und Schülerinnen die Notwendigkeit der Daten sortieren und so mit geeigneten Daten in weiteren Zyklen die Werte genauer analysieren.

Arbeitsphase 1: Diskussion

Um entscheiden zu können, welche Einflussfaktoren für einen Spagatfortschritt relevant sind und welche man in höheren Zyklen besser untersuchen kann, hat sich die Gruppe Gedanken gemacht, welche Faktoren überhaupt für diese Untersuchung in Frage kommen könnten. Um möglichst viel Auswahl zu haben und genügend Daten sammeln zu können, hat man sich auf 17 Faktoren geeinigt.

Die gesammelten Faktoren diese Diskussion über mögliche Korrelationsmerkmale zur Tiefe eines Spagats lassen sich in vier Gruppen einteilen. Biologische-, Körperphysiologische-, alltägliche Gewohnheiten- und Spagat spezifische Faktoren. Der biologische Faktor ist in diesem Fall einzig das biologische Geschlecht. Körperphysiologische Merkmale beinhalten Gewicht, Körpergröße, Beinlängen, Oberschenkelumfänge und körperliche Beschwerden. Die ausgewählten Faktoren, Beruf, tägliche Sitz-Zeit, aktuelle und ehemalige Hobbies, Ernährungsweise, Stresslevel und Verwendung von Entspannungstechniken, kann man zu den alltäglichen Gewohnheiten zuordnen. Die spezifischen Faktoren für den Spagat sind die Motivation, die Vorerfahrungen mit dem Spagat, individuelle Trainingsintervalle pro Woche, sowie die von den Probepersonen verwendete Trainingstechnik. Zusätzlich zu diesen Faktoren, hat sich die Gruppe entscheiden jeweils die Höhe der drei Spagattypen (Männerspagat, Frauenspagat recht und links) zu messen, sowohl vor als auch nach dem Aufwärmen der Beine, um später die Faktoren mit der Höhe im Spagat vergleichen zu können.

Arbeitsphase 2: Erstellung des Umfragebogens und des Datenblatts für die Messreihe

Die Ergebnisse der Diskussion wurden verwendet, um einen Umfragebogen und eine Tabelle zu erstellen. Aufgrund der Tatsache, dass auch eine Messreihe notwendig ist, um die erforderliche Daten zu erheben, wurde ein Blatt zum Eintragen der Messwerte für die Messreihe erstellt. Sowohl der Umfragebogen als auch das Messblatt befinden sich auf dieser Seite.

Arbeitsphase 3: Datenerhebung

Um eine bestmöglichste Analyse über die Einflussfaktoren des Spagats zu erreichen, benötigte die Gruppe eine möglichst große Menge an Daten. Allgemein kann man die mit den Umfragebögen und dem Datenblatt gefragte und gemessene Personen, in vier verschiedene Gruppe einteilen.

Die erste Gruppe bestand aus zehn Mitgliedern eines Karnevalsvereins, die alle in der Garde tanzten und jede Woche die Tanzfigur Spagat für ihre Tänze benötigten. Hier wurden jede Woche Messungen durchgeführt, um eventuell in weiteren Zyklen den Spagatfortschritt bei regelmäßigem Training modellieren zu können. Die zweite Gruppe bestand aus 11 Leuten, die sich aus Freunden, Bekannten und Verwandten der Gruppenteilnehmer zusammensetzten. Um eine größere Anzahl an Probepersonen zu erreichen, fragte die Gruppe eine Physiotherapieschule, in der sich zwei Klassen, insgesamt 32 Personen, freiwillig meldeten, um an diesem Projekt teilzunehmen. Die vierte Gruppe besteht aus den Gruppenteilnehmern dieses Modellierungsprojektes.

Insgesamt wurden also von 56 Personen jeweils 27 Daten erhoben und in einer Tabelle zusammengefügt. Da diese Datenmenge sehr groß ist, ist hier nur ein Teil der Tabbelle abgebildet:

Um die Tabelle übersichtlich zu gestalten sind im Folgenden die Abkürzungen für einige Wörte aufgelistet, die wir in unsere Tabelle verwendet haben:

Nach der einmaligen Datenerhebung hat sich die Gruppe entschieden eine Gruppe für einen längeren Zeitraum zu betrachten. Da die Gardegruppe jede Woche einmal trainierte, führte man in einem gewissen Zeitraum vier Messungen durch. Auch die Gruppe der Physiotherapie Auszubildende wurden für diese Messungen gefragt. Leider konnte man hier keine genauen Messungen vornehmen, da der Kontakt fehlte. Auch die langfristige Messung mit der Tanzgruppe, führe zu keinem genauen Ergebnis, denn aufgrund der geringen Zeit kamen nicht genügend Daten zusammen, um eine Datenanalyse für den Spagatfortschritt innerhalb eines Zeitraumes durchführen zu können. Die Gruppe hat sich deshalb dazu entschieden, sich nur auf die Faktoren, die für den Abstand "Leiste-Boden" relevant sind zu untersuchen.

Diese Abbildung zeigt die gemessenen Daten der Tanzgruppe innerhalb von fünf Wochen:

Arbeitsphase 4: Datenanalyse

Mit Hilfe eines Tabellenkalkulationsprogramms, wurde eine Boxplot Analyse durchgeführt, um einen Überblick über die Datenmenge zu erhalten. Da man Faktoren wie Beruf, Hobby, Ernährung, sowie Technik schwer skalieren kann und es da teilweise nur drei Werte geben würde, hat sich die Gruppe entschieden nur folgende Faktoren zu betrachten: Die Höhe des Spagats bei allen drei Spagattypen unter separater Betrachtung der Geschlechter, das Alter der Versuchspersonen, sowie deren Gewicht und der Mittelwert aus den Beinlängen und der Mittelwert des Oberschenkelumfangs.

Box Plot

Ein Box Plot dient zu Übersicht der gesammelten Daten. Hier wird sichtbar, wie die Werte der Daten verteilt sind. Der Strich in der Box ist der Median (M). An ihm kann man ablesen, dass die Hälfte der Daten größer gleich und die andere Hälfte der Daten kleiner gleich diesem Wert entsprechen. Man kann diese Stelle in der Datenmenge, an dem er liegt wie folgt berechnen:

${\textstyle M={\frac {n+1}{2}}}$

Die berechnete Stelle kann nun gefunden und der Datenwert dem Median zugeordnet werden. Das n in der Gleichung steht für die Anzahl an Datenwerten. Wichtig ist den Median nicht mit dem Mittelwert zu verwechselt, denn dieser gibt den Durchschnitt der Daten und nicht die Mitte an.

In der Box liegen insgesamt 50% der Werte, denn unter dem sogenannten Unterem Quartil (Q2) liegen die unteren 25% der Daten und über dem Oberen Quartil (Q1) liegen die oberen 25% der Daten. Das untere und das obere Quartil sind die untere und obere Grenze der Box. Die Stelle der Grenzen kann wieder mit einer Formeln berechnet und dann diesen Datenwert dem Quartil zugeordnet werden:

${\textstyle Q1={\frac {3(n+1)}{4}}}$

${\textstyle O2={\frac {n+1}{4}}}$

Die Bereich, in dem der obere (W1) und untere Whisker (W2) liegen kann, lässt sich aus dem 1,5-fachen Abstand zwischen den beiden Quatilen berechnet werden. Dieser wird Abstand wird Interquartilsabstand (IQA) genannt und ist das erlaubte Intervall, in dem die Whisker liegen dürfen:

${\textstyle IQA=Q1-Q2}$

Im Normalfall sind die Whisker das Minimum und oder Maximum der Daten. Liegt der kleinste/größte Datenwert über der Intervallgrenze, beziehungsweise unter den Whiskern, dann zählen diese als Ausreiser, also sind diese ungewöhnliche Werte für diese Datenmenge. Der Whisker ist dann der nächst höhere/niedrigere Datenwert im erlaubten Intervall.

${\textstyle W1=Q1+1.5*IQR}$ oder Maximum

${\textstyle W2=Q2-1.5*IQR}$ oder Minimum

Ergebnisse der Box Plot Analyse

Diese Abbildungen zeigen die Datenanalyse mit Hilfe des Boxpots. Die Ergebnisse geben eine grobe Übersicht über die Verteilung der Daten. Auch wird hier der Mittelwert mithilfe eines x angezeigt. Auf diesen wird im nächsten Abschnitt näher eingegangen. Diese Analyse zeigt, dass 50% der Befragten zwischen 20 und 24 Jahre alt sind. Besonders auffällig ist, dass die alle Datenwerte bei jedem Spagattyp, egal ob aufgewärmt oder nicht aufgewärmt bei den Frauen tiefer liegen wie bei den Männern. Hier könnte man vermuten, dass Männer schlechter ins Spagat kommen als Frauen. Zusätzlich kann man sagen, dass egal ob Mann oder Frau die Datenverteilung bei allen Spagattypen bei aufgewärmten Zustand tiefer sind als beim unaufgewärmten. Die Datenverteilungen der restlichen Kategorien (Beinlänge, Gewicht, Oberschenkelumfang) kann man am Boxplot gut ablesen:

Mittelwerte

Zusätzlich zur Box Plot Analyse wurde in einer Tabelle die Mittelwerte festgehalten. Diese Mittelwerte zeigen den Durschnitt der untersuchten Faktoren. Zum Beispiel liegt das Durchschnittsalter der Probanden dieser Datenerhebung bei 24 Jahren und wiegen um die 70 Kilogramm. Außerdem kann man am Mittelwert ablesen, dass die Frauen im Durchschnitt tiefer ins Spagat kommen als die Männer und dass das Männerspagat der Spagattyp ist, an dem alle Geschlechter am höchsten sind. Dies hat auch schon die Boxplot Analyse gezeigt. Auch ist das Frauenspagat mit dem linken Bein nach vorne gespreizt, besser als das Frauenspagat mit dem rechten Bein nach vorne. Dies hat die Gruppe sehr gewundert, denn sie hat vermutet, dass es anders herum der Fall ist, denn mehr Menschen sind Rechtsfüßler als Linksfüßler. Zusätzlich lässt sich bei jedem Spagattyp eine starke Verringerung der Höhe des Spagats nach dem Aufwärmen feststellen. Dies lässt darauf schließen, dass das Aufwärmen essenziel für eine niedrigere Höhe des Spagats ist. Auch dies wurde vorher mit der Boxpot Analyse gezeigt.

Die Formel für den Mittelwert ${\bar {x}}$ ist wie folgt:

${\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}{x_{i}}={\frac {x_{1}+x_{2}+\dots +x_{n}}{n}}$

Mit Worten: Der Mittelwert ist die Summe aller Datenwerte durch die Anzahl der Datenwerte.

Arbeitsphase 5: Abschließende Ergebnisse

Zum Ergebnis des ersten Zyklus lässt sich sagen, dass man viele Faktoren untersuchen kann und dass die Datenanalyse sehr von der Menge der Daten abhängig ist. Je mehr Daten man hat, desto besser lässt sich darüber eine allgemeingültige Aussage treffen. Allerding hängt dies auch stark von der Verteilung der Daten ab. In diesem Projekt wurden zum Beispiel besonders viele junge Erwachsene zwischen 18 und 30 Jahren befragt, weshalb man keine genauen Aussagen über die Spagathöhe von ältere Menschen treffen kann. Dazu müssten weiter Probanden befragt und bemessen werden. Außerdem sagt der Mittelwert zwar die Durchschnittswerte an, aber ist dennoch schwierig zu interpretieren, da hier zu wenige Messdaten vorliegen, sowie der Zeitraum für solch eine genaue Analyse zu knapp ist. Durch sogenannte Ausreise können die Ergebnisse sehr von der Norm abweichen, wenn zu wenige Daten vorhanden sind.

Dieser Zyklus eignet sich gut für die Sekundarstufe I, denn die Schüler und Schülerinnen können hier lernen, geeignete Faktoren zu wählen, diese dann in einer geeigneten Tabelle mit einem Tabellenkalkulationsprogramm darzustellen und eine Datenanalyse mit den Mittelwerten oder mit Hilfe einer Boxplot Analyse, die einfache Formeln beinhalten, durchführen zu können. Über diese Datenanalyse sollten dann auch mit der Klasse diskutiert und Folgerungen daraus geschlossen werden.

Im folgenden Zyklus werden die Faktoren weiter untersucht.

Sek II / Zyklus II

Dieser Zyklus befasst sich mit den Abweichungen der Messdaten, um eine genaue Interpretation der Daten und eine kritische Prüfung der Ergebnisse zu ermöglichen. Für die Fehlerrechnungen wurde eine Sonderform der Gausschen Fehlerfortpflanzung verwendet, die Maximalfehlerabschätzung. Ebenso werden die Korrelationen verschiedener Faktoren mit der Spagathöhe untersucht. Anschließend liefert die lineare Regression Aussagen über die Art von den Zusammenhängen.

Herleitung der Korrelationsformel nach Pearson

Der Pearson Korrelationskoeefizient $r_{xy}$ beschreibt den ungerichteten Zusammenhang zwischen Zwei Variablen $\left\{(x_{1},y_{1}),\ldots ,(x_{n},y_{n})\right\}$. Hierbei existieren verschiedene Ausprägungen:

• Positiver Zusammenhang: Je höher der Wert einer Variable, desto höher der Wert der anderen Variable. Je niedriger der Werte einer Variable, desto niedriger der Wert der anderen Variable.
• Negativer Zusammenhang: Je höher der Wert einer Variable, desto niedriger der Wert der anderen Variable. Je niedriger der Wert der einen Variable, desto höher der Wert der anderen Variable
• Kein Zusammenhang: Die Höhe der Werte auf beiden Variablen variieren nicht miteinander. Eine Veränderung der einen Variable hat keinen Einfluss auf die Veränderung der anderen Variable.

Um herauszufinden, ob zwischen 2 Variablen eine Korrelation vorliegt, muss die Kovarianz (als Zwischenschritt) berechnet werden. Hierzu untersucht man, wie weit die Variablen miteinander kovariieren. Mit der Kovarianz lässt sich also bestimmen, wie sich die relativen Positionen (Abweichungen vom Mittelwert) von gepaarten Messwerten aus zwei Variablen zueinander verhalten. Vorab hilft uns die Kovarianz die Richtung des Zusammenhanges herauszufinden (z.B. positives Vorzeichen meint positiven Zusammenhang), jedoch kann diese keine Aussagen über die Stärke des Zusammenhangs machen. Die Kovarianz wird definiert als:

Da die Kovarianz nur hinsichtlich ihres Vorzeichens interpretiert werden kann, muss diese schließlich durch das Produkt der Standardabweichungen ${\textstyle s_{x}}$ und ${\textstyle s_{y}}$ dividiert werden, sodass wir als Quotient $r_{xy}$ den Pearson Korrelationskoeffizient (oder auch: Produkt-Moment-Korrelation) erhalten:

Die Standardabweichungen dienen als Maß, wie stark die Messwerte um den Mittelwert der Verteilung streuen. Wenn die Standardabweichung einer Variable groß ist, bedeutet dies, dass die Datenpunkte der Variablen weit gestreut sind und im Durchschnitt stark von ihrem Mittelwert abweichen. Das könnte darauf hindeuten, dass es eine große Heterogenität in den Daten gibt. Die Formel zum Berechnen der Standardabweichung lautet: ${\textstyle s_{x}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}}$. Setzt man diesen Zusammenhang in die Formel für $r_{xy}$ ein erhält man:

$$r_{xy}={\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{{\sqrt {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}{\sqrt {\sum _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}}}}$$

In diese Formel kann man die erhobenen Messdaten$\left\{(x_{1},y_{1}),\ldots ,(x_{n},y_{n})\right\}$ einsetzen, um den Korrelationszusammenhang herauszufinden. Mit dem Tabellenkalkulationsprogramm Excel wurde der Korrelationskoeffizient für den Zusammenhang zwischen Alter (X) und Höhe des Männerspagates (Y) im nicht aufgewärmten Zustand bestimmt.

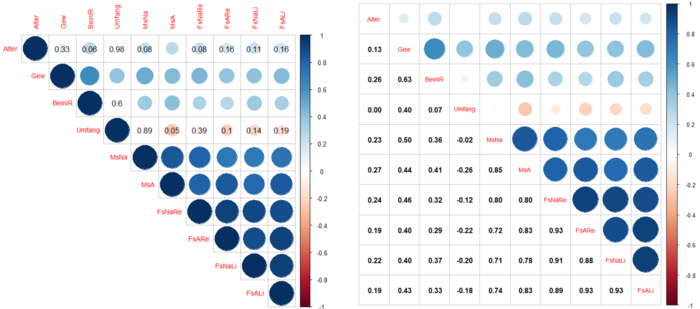
Korrelationsmatrix

Eine Korrelationsmatrix lässt sich mit der Statistik Software RStudio leicht erstellen. Hierzu wird das Datenpaket "corrplot" verwendet. Die folgenden Befehle werden aufgelistet.

Zuerst wird eine Matrix aus den metrischen Variablen definiert, welche die Korrelationen zwischen den Einflussfaktoren berücksichtigt.

korrelation <- Data1[c("Alter","Gew","BeinlR","Umfang","MsNa","MsA","FsNaRe","FsARe","FsNaLi","FsALi")]

Für die erste Korrelationsmatrix, sollen die P-Werte dargestellt werden, welche über die Funktion cor.mtest() zusammen mit den Konfidenzintervallen berechnet werden.

korrelationpWerte <- cor.mtest(korrelation)

Der Corrplot- Befehl liefert schließlich Kreisdiagramme, welche teilweise Aussagen über den p-Wert machen. Sobald die p-Werte angezeigt werden, wissen wir, dass die Korrelation zwischen den jeweiligen Faktoren nicht signifikant ist. Dies ist der Fall, wenn das Standardsignifikanzniveau von 0,05 überschritten wird.

corrplot(korrelationm, p.mat=korrelationp$p, insig = "p-value", method = "pie", type= "upper",tl.cex = 0.9)

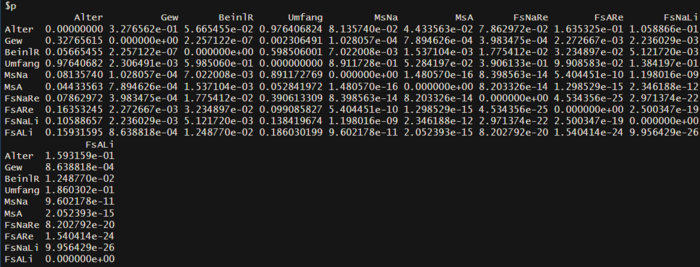
Für die zweite Korrelationsmatrix (rechts) wird zunächst die Korrelation der Matrixelemente untereinander bestimmt mit der Funktion "cor()".Hierbei handelt es sich um die Pearson Korrelation.

korrelationsmatrix <- cor(korrelation)

Mit dem "Corrplot-Mixed-Befehl" wird die Matrix symmetrisch aufgeteilt. Auf der rechten Seite oberhalb der Diagonalelemente, sind Kreise dargestellt, welche die Stärke des Zusammenhangs durch Farben illustrieren. Unterhalb der Diagonalelemente sind die jeweils bestehenden Korrelationswerte numerisch dargestellt.

corrplot.mixed(korrelationmatrix, upper="circle", lower="number",tl.cex = 0.9,  lower.col="black")

Die p-Werte der Pearson Korrelation sind in der folgenden Grafik dargestellt:

korrelationpWerte

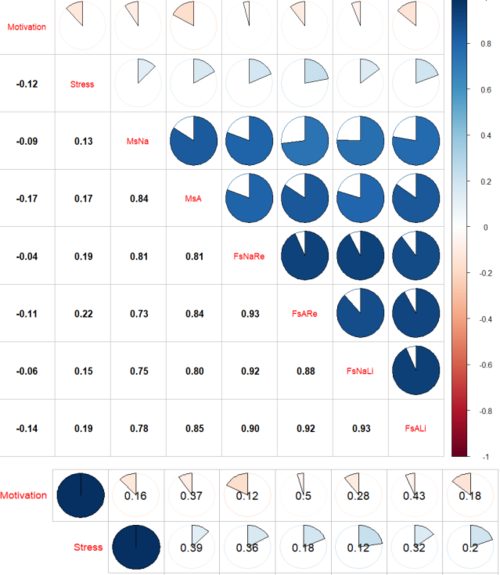
Spearman Rangkorrelation

Die Korrelation nach Spearman bzw. der Spearmansche Korrelationskoeffizient ist ein Maß für den Zusammenhang zweier ordinaler Variablen bzw. einer metrischen und einer ordinalen Variable. Er kann Werte zwischen -1 und +1 annehmen und drückt aus, ob zwei Variablen positiv oder negativ miteinander zusammenhängen. In unserem Fall sind die unabhängigen Variablen (Motivation und Stress) ordinal skaliert. Es werden bei dieser Korrelation die Ränge der Werte verglichen, wehalb keine Voraussetzungen erfüllt werden müssen. Analog zur oben dargestellten Korrelationsmatrix, kann auch eine Matrix für die Variablen Motivation und Stress erstellt werden, um die Auswirkungen auf die verschiedenen Spagattypen zu untersuchen.

Auswertung der Korrelationsanalyse

• Korrelationsanalyse nach Pearson

Aus den verschiedenen Grafiken lässt sich schließen, dass die Faktoren, wie Gewicht und Beinlänge einen Einfluss auf die jeweilige Spagathöhe haben. Faktoren wie der Oberschenkelumfang und das Alter korrelieren eher weniger stark mit der Männerspagathöhe. Es muss schließlich die Annahme berücksichtigt werden, dass wir bei der Pearson Korrelation von einem metrischen Skalenniveau, eine Normalverteilung der Daten und einem Linearen Zusammenhang zwischen den Variablen ausgehen müssen. Bei den gemessenen Größen ist das nur bedingt der Fall, weshalb auch einige Korrelationszusammenhänge nicht signifikant sind. Am stärksten ausgefallen ist das Gewicht. Hier beträgt die Korrelation mit den verschiedenen Spagattypen zwischen 0,4 und 0,5. Wir müssen aber berücksichtigen, dass Männer und Frauen zusammen unter dem Faktor "Gewicht" untersucht werden und Männer im Schnitt mehr wiegen als Frauen. Die Boxplot-Analyse in Zyklus 1 zeigt, dass der Abstand zum Boden bei Frauen bei jedem Spagattyp kleiner ausfällt, als bei Männern. Auch die Beinlänge weist auf ein Zusammenhang mit den verschiedenen Spagattypen hin (Korrelation zw. 0,31 und 0,41). Dabei muss ebenfalls berücksichtigt werden, dass diese auch signifikant ist. Der Oberschenkelumfang ist die einzige Messgröße, welche bei allen Spagattypen nicht signifikant ist. Das Alter ist lediglich beim Männerspagat (nicht aufgewärmt) signifikant. Ebenso fällt die Stärke der Korrelation sehr gering aus.

• Korrelationsanalyse nach Spearman

Die Korrelationsmatrix zeigt, dass die Variblen Motivation und Stress sehr wenig mit der Spagathöhe im aufgewärmten Zustand korrelieren. Das Spearmans Rho liegt bei der Motivation zwischen -0,04 und -0,14 was auf einen maximal sehr geringen Zusammenhang vermuten lässt. Beim Stressfaktor ist die Korrelation mit den Spagattypen ein wenig höher, weil das Spearmans Rho zwischen 0,13 und 0,22 liegt. Interssant ist jedoch, dass der Koeffizient, bei der Motivation negativ und beim Stress positiv ist. Ein negativer Zusammenhang heißt im Fall der Motivation, dass die Probanden, welche eine höhere Motivation an den Tag legen, auch eine geringeren Abstand zum Boden haben, als Personen, welche weniger Motivation aufweisen. Beim Stressfaktor ist der Zusammenhang positiv, was bedeutet, dass Probanden, welche mehr gestresst sind, einen größeren Abstand zum Boden haben, als Personen, welche weniger Stress erfahren. Unter der Korrelationsmatrix sind die p-Werte aufgelistet, welche alle sehr groß sind und die Nullhypothese bestätigen, dass die Variablen auf keinen Zusammenhang hinweisen. Die Signifikanz ist somit nicht erfüllt.

Herleitung Lineare Regression

Die Lineare Regression ist ein statistisches Verfahren zur Modellierung der Beziehung zwischen einer abhängigen Variablen $y$ und einer oder mehreren unabhängigen Variablen $x$. Das Ziel besteht darin, eine Linie zu finden, die die Beziehung zwischen den Variablen am besten beschreibt.

Zunächst nehmen wir an, dass wir $n$ Datenpunkte $(x_{i},y_{i})$ haben, wobei $x_{i}$ die unabhängige Variable und $y_{i}$​ die abhängige Variable ist. Da die Regressionsgerade linear sein soll, modellieren wir die Beziehung zwischen $x$ und $y$ als linear und verwenden die Gleichung $y=mx+b$, wobei $m$ die Steigung und $b$ der $y-Achsenabschnitt$ ist.

Um die beste Passung der Geraden an die vorliegenden Daten zu finden, verwenden wir die Formel der quadratischen Abweichung:

$\sum _{i=1}^{n}(y_{i}-(mx_{i}+b))^{2}$

Die optimalen Werte für $m$ und $b$ können durch Minimierung dieser Funktion gefunden werden. Für die Lineare Regression gibt es Formeln, um $m$ und $b$ direkt zu berechnen:

$m={\frac {n\sum (x_{i}y_{i})-\sum x_{i}\sum y_{i}}{n\sum (x_{i}^{2})-(\sum x_{i})^{2}}}$

$b={\frac {\sum y_{i}-m\sum x_{i}}{n}}$

Auf die Herleitungen dieser Formeln wird verzichtet.

Durch die Berechnung von $m$ und $b$ können wir eine Gerade finden, die die beste Anpassung an die Daten bietet und somit die Beziehung zwischen den Variablen beschreibt.

Auswertung und Ergebnisse der Linearen Regression

Die obigen Abbildungen zeigen Datenwolken mit ihrer jeweils zugehörigen Regressionsgerade. Diese Abbildungen sind eingeteilt auf die drei Spagattypen in Beziehung zur Höhe und Beinlänge, Höhe und Alter, und Höhe und Gewicht, jeweils aufgewärmt und nicht aufgewärmt. Vor der Datenanalyse hat die Gruppe bereits drei Vermutungen aufgestellt:

1. Je länger die Beine, desto tiefer sitzt eine Person im Spagat, wegen den physikalischen Hebelgesetzen.
2. Je älter eine Person ist, desto unbeweglicher ist sie und desto weniger tief kommt sie bei allen Spagattypen runter.
3. Je schwerer die Person, desto tiefer kommt sie in den Spagat, da aufgrund des höheren Gewichts eine größere Gewichtskraft wirkt.

Um zu prüfen ob die Vermutungen durch die Regressionsgeraden die Vermutungen bestätigen, werden diese im folgenden Abschnitt analysiert und interpretiert. Zudem wird noch die Qualität dieser Regressionsgeraden bewertet, um ein reflektiertes Ergebnis zu erhalten.

Betrachtet man die Regressionsgeraden (Alter-Höhe) zu allen drei Spagattypen, sowohl aufgewärmt als auch nicht aufgewärmt, so lassen sich Gemeinsamkeiten feststellen. Die Datenwolke befindet sich hauptsächlich im Bereich der 15- bis 30-Jährigen Probandinnen und Probanden. Danach verteilen sich nur einzelne Datenpunkte im Bereich 30 bis 60. Für das Alter unter 15 Jahren und über 60 Jahren gibt es keine Daten. Die Anzahl dieser Punkte ist im Vergleich zu Anzahl der Punkte im Bereich von 15 bis 30 äußerst gering, sodass keine gleichmäßige Verteilung über die gesamte Altersspanne vorhanden ist. Dies hat zur Folge, dass die Regressionsgerade nicht sehr aussagekräftig ist. Somit kann mit diesen Daten keine präzise und allgemeingültige Aussage über den Zusammenhang zwischen der Spagattiefe und dem Alter getroffen werden. Die Vermutung der Gruppe wurde bestätigt, dennoch hat diese Regressionsgerade nur eine geringe Aussagekraft. Deshalb sollten noch mehr Daten von verschiedenen Altersgruppen erhoben werden, um ein aussagekräftigeres Ergebnis zu erhalten.

Die Gemeinsamkeit der Regressionsgeraden Beinlänge – Höhe für die drei Spagattypen aufgewärmt und nicht aufgewärmt ist, dass in allen Fällen die Gerade eine positive Steigung hat. Daraus folgt: je länger die Beine, desto schlechter der Spagat. Jedoch sind Unterschiede in der Größe der Steigung festzustellen. Bei „Frauenspagat rechts“ entspricht die Steigung m ≈ 0,11 (n.a und a). Bei Frauenspagat links entspricht die Steigung m ≈ 0,5 (n.a und a). Daraus folgt, dass beim „Frauenspagat links“ der Folgerung aus der Positvität der Steigung signifikanter ist.

Die Gemeinsamkeit der Regressionsgeraden Gewicht – Höhe für die drei Spagattypen aufgewärmt und nicht aufgewärmt ist, dass in allen Fällen die Gerade eine positive Steigung hat. Daraus folgt: je schwerer ein Mensch, desto schlechter der Spagat. Jedoch sind Unterschiede in der Größe der Steigung festzustellen. Bei „Frauenspagat rechts“ entspricht die Steigung m ≈ 0,17 (n.a). Bei Frauenspagat links entspricht die Steigung m ≈ 0,48 (n.a). Daraus folgt, dass beim „Frauenspagat links“ der Folgerung aus der Positvität der Steigung signifikanter ist.

In nur einer der Kategorien (Alter-Höhe) wurden die Vermutung der Gruppe durch die Empirie bestätigt. Die Vermutungen zu Gewicht-Höhe und Beinlänge-Höhe bestätigten sich, aufgrund dieser Daten, nicht. Jedoch sind durch die geringe Aussagekraft der Geraden, bedingt durch die geringe Anzahl der Messdaten, diese Bestätigungen nicht bedeutsam.

Die Abbildung über diesem Text zeigt drei Datenwolken mit ihrer jeweiligen zugehörigen Regressionsgerade. Durch die fest verteilten Werte auf der X-Achse ist keine stetige Verteilung der Datenpunkte möglich. Dies hat zu Folge, dass pro Punkt auf der X-Achse mehrere Funktionswerte zugewiesen werden und somit hat man keine homogene Datenwolke. Trends mit Linearer Regression festzustellen ist dementsprechend wenig bedeutsam.

Die letzte Regressionsgerade ist leider ungültig, denn sortiert man die Versuchspersonen innerhalb der Geschlechter anders, so entsteht auch einen andere Regressionsgerade. nur regression bei Modellen die korrelation aufweisen also gewicht

Maximalfehlerabschätzung

Da in diesem Projekt je Probandin oder Proband nur eine einzelne Messung pro Messreihe durchgeführt wurde, entschied sich die Gruppe für eine Maximalfehlerabschätzung um die Messabweichung der Messreihe zu bestimmen. Hierzu müssen systematische und statistische Fehlerquellen berücksichtigt werden. Der systematische Fehler liegt in der Messungenauigkeit des Zollstocks.

Mathematische Grundlagen:

Die Maximalfehlerabschätzung, auch bekannt als maximale Fehlerformel, ist eine Methode zur Abschätzung des maximalen Fehlers, dem die Gauß'sche Fehlerfortpflanzung : zugrunde liegt. Es wird angenommen, dass die Fehler in den Variablen unkorreliert sind und dass die Fehlerbeiträge additiv sind. Der maximale Fehler wird durch folgende Formel berechnet:

$\Delta f_{\mathrm {max} }=\sum _{i=1}^{n}\left|{\frac {\partial f}{\partial x_{i}}}\right|\left|\Delta x_{i}\right|$

$\left|{\frac {\partial f}{\partial x_{i}}}\right|={\text{Partielle Ableitung}}$

$\left|\Delta x_{i}\right|={\text{Standardabweichung}}$

Diese Formel gibt einen oberen Grenzwert für den Fehler an. Da die Beziehung zwischen den Fehlerbeträgen und der Funktion unbekannt sind, soll der Grenzwert möglichst groß sein, dies wird erreicht indem die Beträge summiert werden.

Ergebnis:

Der systematische Fehler beträgt $\left|\Delta x_{1}\right|=0,05cm$. Statistische Fehlerquellen äußern sich hauptsächlich durch Parallaxenfehler. Diese Fehler schleichen sich bei der Messung der Spagat-Variationen ein, da nicht immer senkrecht zum Maßstab abgelesen werden kann. Ebenso tragen Kleidungsstücke dazu bei, dass man nicht exakt den Abstand bemessen kann. Für die statistischen Fehlerquellen nehmen wir eine Messungenauigkeit $\left|\Delta x_{2}\right|=1cm$ an. Die gesamte Fehlerquelle beträgt schließlich $\Delta f_{\mathrm {max} }=1,05cm$

Uni Niveau / Zyklus III

Die Multiple Lineare Regression

Die multiple lineare Regression ist eine statistische Methode, die es ermöglicht, die Beziehung zwischen einer abhängigen Variable und mehreren unabhängigen Variablen zu modellieren. In diesem Beispiel werden wir die mathematischen Grundlagen der multiplen linearen Regression erläutern und den Prozess mit dem R-Code in R Studio demonstrieren.

Mathematische Grundlagen:

Die grundlegende Formel für die multiple lineare Regression lautet: $Y=\beta _{0}+\beta _{1}X_{1}+\beta _{2}X_{2}+\ldots +\beta _{p}X_{p}+\varepsilon$

• $Y$ ist die abhängige Variable
• $X_{1},X_{2},\ldots ,X_{p}$ sind die unabhängigen Variablen
• $\beta _{0},\beta _{1},\ldots ,\beta _{p}$ sind die Regressionskoeffizienten
• $\varepsilon$ ist der Fehlerterm

Das Ziel ist es, die Koeffizienten so zu schätzen, dass die quadratischen Abweichungen zwischen den beobachteten und vorhergesagten Werten minimiert werden.

Schritt 1: Vorraussetzungen prüfen

In diesem Abschnitt werden die Voraussetzungen geprüft, ob eine multiple lineare Regression sinnvoll und durchführbar ist. Aus der Datenerhebung wird die abhängige Variable (MsNa) Höhe des Männerspagates im nicht aufgewärmten Zustand mit den unabhängigen Variablen Alter und Gewicht untersucht. Dieser Analyseprozess wird im folgenden Ausgeführt

Metrische Abhängige Variable (AV): Die Variable wird auf einer gleichabständigen Skala gemessen. Diese Voraussetzung ist erfüllt da wir die Männerspagathöhe im nicht aufgewärmten Zustand untersuchen. Diese Variable ist metrisch, da wir die Höhe in Centimeter gemessen haben.

Linearität zwischen unabhängigen Variablen und abhängiger Variable: Die Beziehung zwischen den unabhängigen Variablen und der abhängigen Variable sollte linear sein. Dies bedeutet, dass Veränderungen in den unabhängigen Variablen zu proportionalen Veränderungen in der abhängigen Variable führen sollten. Eine visuelle Überprüfung durch Streudiagramme kann helfen, diese Linearität zu überprüfen.

In R-Studio lässt sich zudem mit den folgenden Befehlen eine Regressionsanalyse durchführen.

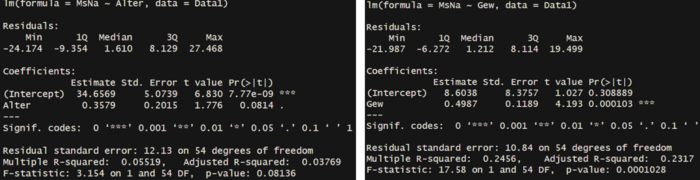
Reg1 <- lm(MsNa~Alter, data=Data1)

summary(Reg1)

In unserem Fall sind die Beziehungen nur bedingt linear.Das Streudiagramm, welches die Variablen Alter und Männerspagathöhe untersucht, zeigt dass der Zusammenhang nur schwach linear ist. Der p-Wert aus der Regressionsanalyse liegt bei 0,08136, was zu einer Bestätigung der Nullhypothese führt, sodass das Modell keinen Erklärungsbeitrag leistet. Hier liegen zu wenige Messungen vor, welche Versuchspersonen mit höherem Alter untersuchen. Die Probanden waren fast alle im Alter zwischen 15 und 30, wodurch die lineare Regression nur bedingt sinnvoll ist. Trotzdem wird mit dieser Voraussetzung gearbeitet, weil die Datenerhebung sonst keine besseren unabhängigen und "linearen" Variablen wie Alter und Gewicht bereitstellt.

Normalverteilte Residuen: Die Residuen, die Differenzen zwischen den beobachteten und den vorhergesagten Werten der abhängigen Variable, sollten normal verteilt sein. Dies bedeutet, dass die Residuen eine Glockenkurvenform haben sollten. Normalverteilte Residuen sind wichtig, um sicherzustellen, dass die statistischen Tests und Konfidenzintervalle gültig sind. Ein Q-Q Diagramm lässt sich mit folgenden Befehlen leicht in Rstudio erstellen:

modell <- lm(MsNa ~ Alter+Gew, data=Data1)

plot(modell, 2)

In diesem Beispiel sind die Datenpunkte relativ nah an der gestrichelten Linie, welche die ideale Normalverteilung anzeigt. An den Enden liegen die Werte etwas weiter weg, was jedoch nicht allzu schlimm ist, da wir nur von in etwa Normalverteilten Residuen ausgehen.

Homoskedastizität (Gleichmäßige Streuung der Residuen):

Die Streuung der Residuen sollte über alle Werte der unabhängigen Variablen gleichmäßig sein. Homoskedastizität stellt sicher, dass die Präzision der Vorhersagen konstant ist und nicht von der Menge der unabhängigen Variablen abhängt. Die Homoskedastizität kann mit dem Befehl

plot(modell, 1)

in RStudio analysiert werden.

In diesem Fall streuen die Residuen nicht wirklich gleichmäßig, was man daran erkennt, dass die rote Linie nicht auf der Nulllinie (gestrichelte Linie) liegt. Einzelne Werte (z.B 31, 10 oder 23) streuen mehr, was zu einer Heteroskedastizität führt.

Keine Multikollinearität: Die unabhängigen Variablen sollten nicht zu stark miteinander korreliert sein, da dies zu Schwierigkeiten bei der Interpretation der einzelnen Variablen und zu instabilen Schätzungen führen kann. Wenn zwei oder mehr unabhängige Variablen eng miteinander verbunden sind oder fast dasselbe messen, wird der zugrunde liegende Effekt, den sie messen, doppelt (oder mehr) über die Variablen hinweg berücksichtigt. Es wird schwierig oder unmöglich zu sagen, welche Variable die unabhängige Variable wirklich beeinflusst. Multikollinearität kann durch Berechnung des Varianzinflationsfaktors (VIF) überprüft werden. Ein Inflationsfaktor mit großer Varianz (>5) (VIF) bei einer unabhängigen Variablen weist auf eine stark kollineare Beziehung zu den anderen Variablen hin.

Der VIF liegt bei unserem Modell für Alter und Gewicht bei 1.018069. Dieser kann mit der Funktion VIF() in RStudion bestimmt werden. Der Wert ist sehr klein, weshalb man von keiner oder zumindest sehr schwachen kollinearen Beziehung zwischen den Variablen Alter und Gewicht ausgehen kann. Anhand der in Zyklus II ausgegebenen Korrelationsmatrix lässt sich ebenfalls identifizieren, dass die 2 Variablen nicht miteinander korellieren.

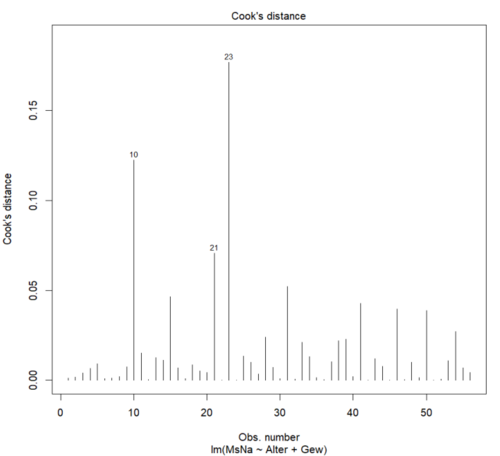
Keine einflussreichen Fälle (Ausreißer): Einflussreiche Fälle können die Ergebnisse einer Analyse stark beeinflussen. Diese Fälle liegen außerhalb vom Zentrum und anderen Datenpunkten, und können somit eine große Hebelwirkung auf die Regressionsgerade haben. Das Identifizieren und Untersuchen von Ausreißern ist wichtig, um sicherzustellen, dass sie nicht die Schlussfolgerungen dominieren. Einfluss kann durch statistische Maße wie Cook's D oder durch visuelle Überprüfungen in Ausreißerdiagrammen festgestellt werden. Mit dem Befehl folgt das Diagramm:

plot(modell, 4)

Auf der x-Achse ist die Probandenanzahl aufgelistet, wobei jedem Fall eine Cook´sche Distanz zugeordnet wird. Die Werte mit großer Distanz müssen hinsichtlich ihrer Plausibiltät überprüft werden. In unserem Beispiel (Nummer 10, 21 und 23) wird die Spagathöhe abhängig von Alter und Gewicht untersucht. Man erwartet eher das Personen mit mehr Gewicht und/oder höherem Alter, auch eher unbeweglicher sind (größere Distanz zum Boden). Diese Fälle widerlegen die Erwartungswerte, weshalb die Distanz größer ist. Trotzdem sind die Fälle alle plausibel und müssen berücksichtigt werden.

Schritt 2: Interpretation des Modells

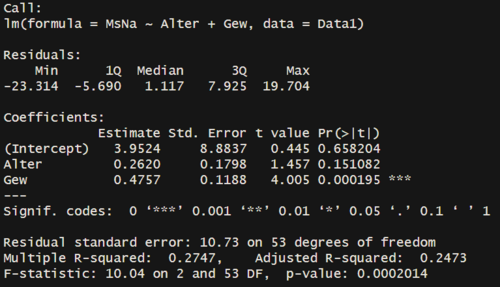
Die Summary- Funktion in R liefert eine deskriptive Statistik für unsere Daten. Diese lässt sich erstellen mit den Beiden Befehlen:

modell <- lm(MsNa ~ Alter+Gew, data=Data1)

summary(modell)

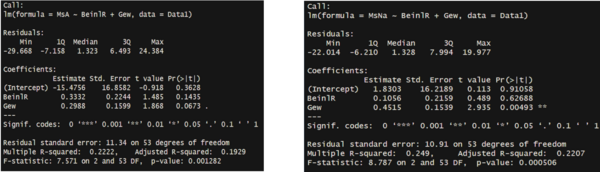
• Die F-Statistik sagt aus, dass unser Modell ein Erklärungsbeitrag leistet, da die Nullhypothese verworfen werden kann (p<0,05).
• Das Multiple R^2 sagt aus, dass 27,47 % der Varianz der abhängigen Variablen (Höhe des Männerspagates-MsNa) erklärt werden kann.
• Der t-Wert ist ein Maß dafür, wie stark sich der Mittelwert einer Stichprobe von einem erwarteten Wert (Hypothesenwert) unterscheidet.Er wird verwendet, um zu prüfen, ob diese Differenz statistisch signifikant ist.
• Der p-Wert (Signifikanzniveau) gibt die Wahrscheinlichkeit an, dass die beobachtete Differenz zwischen den Mittelwerten aufgrund des Zufalls auftritt.Ein kleiner p-Wert (typischerweise < 0,05) deutet darauf hin, dass die Differenz statistisch signifikant ist. Ein hoher p-Wert (> 0,05) zeigt, dass die Differenz nicht signifikant ist. Wenn der p-Wert niedrig ist, lehnen wir die Nullhypothese ab und akzeptieren die Alternativhypothese.Der p- Wert wird von vielen Faktoren beeinflusst: Stichprobengröße, der Verteilung der Daten, die Unabhängigkeit der Messgrößen und Homoskedastizität.
• In unserem Fall ist die Signifikanz nur beim Gewicht erfüllt. Hier verwerfen wir die Nullhypothese, welche Aussagt, dass die unabhängige Variable keinen signifikanten Einfluss auf die abhängige Variable hat. Das Alter hat jedoch keinen signifikanten Einfluss auf die abhängige Variable.
• Mit der Estimate (Schätzung) kommt man zum Schluss: Erhöhe ich die jeweils unabhängige Variable um eine Einheit, dann steigt die Höhe im Männerpagat um 0.262 Einheiten (Alter) und um 0.4757 Einheiten (Gewicht).Mit diesen Schätzwerten kann man die Regressionsgleichung erstellen und erhält eine Prognose.
• Das Intercept ist der vorhergesagte Wert, den wir erwarten würden, wenn alle unabhängigen Variablen null wären. Dieser Grundwert liefert uns den Ebenenschnitt (z-Achse), wenn die unabhängigen Variablen innerhalb der multiplen Regression den Wert 0 haben.
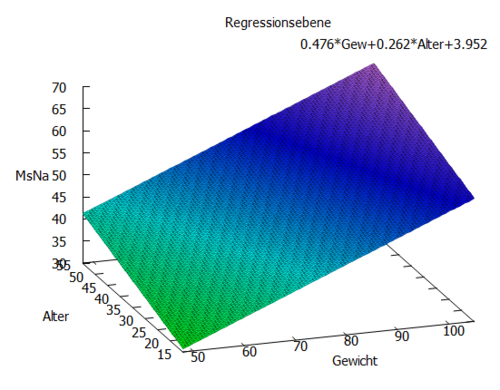
• Regressionsgleichung: MsNa = 3.952 + 0.476 * Gew + 0.262 * Alter

Schritt 3: Visualisierungsprozess

Umsetzung der multiplen linearen Regression in R Studio

Mithilfe R Studio kann datenbasierend eine Regressionsebene erstellt werden. In der folgenden Tabelle wird der Algorithmus genauer, mittels Verwendung der Daten(Männerspagat nicht aufgewärmt, Alter und Gewicht), erklärt.

Algorithmus zum Erstellen einer Regressionsebene

Bezeichnung	Befehl in R	Beschreibung
Lineare Regression mit 2 Variablen	mod3 <- lm(MsNa ~ Gew + Alter, data = Data1	Es wird eine lineare Regression (lm) mit zwei unabhängigen Variablen (Gew=Gewicht und Alter) und einer abhängigen Variable (MsNa=Männerspagat nicht aufgewärmt) durchgeführt. Das Ergebnis wird im Modellobjekt mod3 gespeichert. Die Modellierungsdaten werden aus der Datenerhebung=Data 1 entnommen.
Daten für die Vorhersage erstellen	Gew_range <- seq(min(Data1$Gew), max(Data1$Gew), length.out = 40) Alter_range <- seq(min(Data1$Alter), max(Data1$Alter), length.out = 40) grid <- expand.grid(Gew = Gew_range, Alter = Alter_range)	Ein Gitter von Werten für Gew und Alter wird erstellt, um Vorhersagen zu generieren. seq erstellt Sequenzen von Werten zwischen dem Minimum und Maximum der jeweiligen Variablen. expand.grid erstellt alle möglichen Kombinationen von Gew und Alter in einem Gitter.
Vorhersagen treffen	vals <- predict(mod3, newdata = grid)	Mit dem Modell werden Vorhersagen (predict) für die im vorherigen Schritt erstellten Datenpunkte getroffen.
Datenrahmen für Vorhersagen erstellen	MsNa <- matrix(vals, nrow = length(Gew_range), ncol = length(Alter_range)) plane <- MsNa	Die Vorhersagen werden in eine matrix MsNa umgewandelt, die für die Erstellung der Regressionsebene verwendet wird.In R steht nrow() für die Matrixzeilenanzahl und ncol() für die Spaltenanzahl. Die erstellte Matrix (MsNa) wird als Ebene (plane) definiert.
Paket Plotly laden	install.packages("plotly") library(plotly)	Plotly ermöglicht das Erstellen von 3D Diagrammen, welche aus den gesammelten Daten erstellt werden können.
Daten für Scatter Plot	scatter_data <- data.frame(Gew = Data1$Gew, Alter = Data1$Alter, MsNa = Data1$MsNa)	Der Datenrahmen für das Streudiagramm (scatter) wird aus den 3 Variablen (Alter, Gewicht und Männerspagat n.a) festgelegt.
Scatter-Plot erstellen	p <- plot_ly(data = scatter_data, z = ~MsNa, x = ~Alter, y = ~Gew, type = "scatter3d", mode = "markers", marker = list(color = ~MsNa, colorscale = 'Viridis'), opacity = 0.8) %>% add_markers()	Ein 3D-Scatter-Plot (scatter3d) mit den zugewiesenen Variablen x,y und z wird erstellt, wobei die Farbe (color) der Punkte, durch die Werte (colorscale = 'Viridis') von MsNa bestimmt wird. Die Transparenz der Datenpunkte wird durch den Befehl "opacity()"festgelegt.
Regressionsebene hinzufügen	p %>% add_surface(z = ~plane, x = ~Alter_range, y = ~Gew_range, showscale = TRUE) %>% layout(scene = list(xaxis = list(range = c(min(Data1$Alter), max(Data1$Alter))),yaxis = list(range =c(min(Data1$Gew), max(Data1$Gew))),zaxis = list(range = c(min(Data1$MsNa), max(Data1$MsNa)))), showlegend = FALSE)	p %>%add_surface(...) fügt der bestehenden Plotly-Grafik p eine 3D-Regressionsfläche hinzu. Die add_surface-Funktion wird verwendet, um die Oberfläche mit den spezifizierten x-, y- und z-Werten hinzuzufügen. Mit layout(scene = list(...))werden bestimmte Layout-Optionen für die Szene festgelegt. Diese Optionen umfassen die Festlegung der Achsenbereiche (xaxis, yaxis, zaxis) basierend auf den Daten in Data1. Die range-Optionen werden verwendet, um die Achsenlimits festzulegen. showscale = TRUE zeigt die Farbskala für die Regressionsebene an.
Regressionsgleichung bestimmen	mod3 <- lm(MsNa ~ Gew + Alter, data = Data1) coefficients <- coef(mod3) equation <- paste("MsNa =", round(coefficients[1], 3), "+", round(coefficients[2], 3), "* Gew +", round(coefficients[3], 3), "* Alter") cat("Regressionsgleichung:", equation)	coef() wird verwendet, um die Koeffizienten der Regressionsgeraden zu berechnen.Die Gleichung (equation) repräsentiert die Regressionsebene. round() wird verwendet, um die Koeffizienten auf drei Dezimalstellen zu runden.cat() gibt die Gleichung der Regression aus.

Visualisierung mit R

Führt man den oben illustrierten Algorithmus durch, erhält man eine Regressionsebene, welche die Höhe des Männerspagates (n.a) auf der z-Achse in Abhängigkeit der Variablen Gewicht (x-Achse) und Alter(y-Achse) charakterisiert.

Die untere Abbildung zeigt die Regressionsebene aus der Sicht eines Beobachters, welcher sich unter der Ebene befindet. Hierbei kann man erkennen , dass sich die Datenpunkte (x,y,z) besonders durch den Einfluss des Alters in einem gewissen Bereich im Raum auffinden lassen (hauptsächlich im Intervall [15J-25J]). Anhand der 2 Dimensionalen Streudiagramme lässt sich dieser Zusammenhang ebenfalls darstellen. Problematisch sind fehlende Werte für hohes Gewicht und zunehmendes Alter, wodurch die Regressionsebnene nur grob geschätzt werden kann. Ebenso erkennt man, dass die Abstände der Datenpunkte von der Ebene jeweils sehr groß ausfallen, was darauf hindeutet, dass eine lineare Regressionsebene nur bedingt sinvoll ist und eventuell ein nicht linearer Zusammenhang vorliegen könnte

Visualisierung mit Maxima

Auch in Maxima kann die Ebene gezeichnet werden. Hierzu benötigt man den folgenden Code:

• load(draw);

• MsNa(Gew, Alter) := 3.952 + 0.476 * Gew + 0.262 * Alter;

• plot3d(MsNa(Gew, Alter), [Gew, 48, 105], [Alter, 15, 55],[grid, 100, 100], [title, "Regressionsebene"],[xlabel, "Gewicht"], [ylabel, "Alter"], [zlabel, "MsNa"],[color, blue]);

Weitere Regressionsebenen basierend auf unserer Datenerhebung

Im folgenden werden analog zur obigen dargestellen multiplen Regression weitere Regressionsebenen erstellt. Hierbei berücksichtigen alle Regressionsebenen die zwei unabhängigen, metrisch-skalierten Variablen Gewicht und Beinlänge.

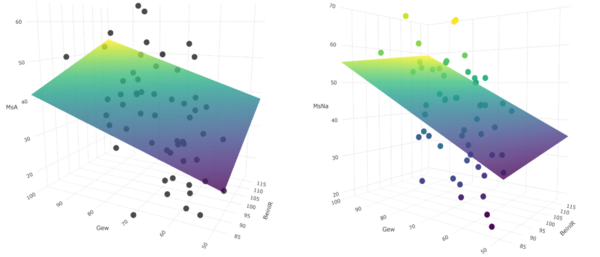
Die untere Abbildung zeigt die Schätzung der Regressionsebene für die abhängige Variable MsNa (Männerspagat nicht aufgewärmt) unter dem Einfluss der beiden unabhängigen Variablen Gewicht (x-Achse) und Beinlänge (y-Achse).

Es wurden bewusst die metrischen Variablen Gewicht und Beinlänge verwendet, da diese unabhängig sind, annähernd normalverteilt sind und bei der linearen Regression einen zumindest schwachen linearen Zusasammenhang aufzeigen.

*Vergleich Männerspagat aufgewärmt vs. Männerspagat nicht aufgewärmt

Nun können wir die Regressionsebene, sowie die deskriptive Statistik des Männerspagats im nicht aufgewärmten Zustand (MsNa) mit dem aufgewärmten Zustand (MsA) vergleichen:

Auffällig beim Vergleich ist die Position der Regressionsebenen. Die erste Ebene beschreibt die Prognose der Männerspagathöhe im aufgewärmten Zustand (MsA). Diese ist im Vergleich zur Ebene des Männerspagats im nicht aufgewärmten Zustand (MsNa) deutlich steiler geneigt. Diese Tatsache ist darauf zurückzuführen, dass die Probanden im aufgewärmten Zustand durchschnittlich 6-7 cm weiter in Richtung Boden kommen (siehe Boxplot Zyklus 1). Dadurch nimmt jedoch auch die Streuung der Daten zu, was man am Bestimmtheitsmaß auslesen kann. Im aufgewärmten Zustand sind Beinlänge und Gewicht keine signifikanten Merkmale für die Höhe im Männerspagat. Im unaufgewärmten Zustand (MsNa) hat zumindest das Gewicht einen signifikanten Einfluss auf die Höhe im Männerspagat.

*Vergleich Frauenspagat (links) vs. Frauenspagat (rechts) im aufgewärmten Zustand:

Interessant ist auch der Unterschied zwischen den Frauenspagattypen. Hierzu wird das Frauenspagat mit linkem Bein vorne (FsALi), welches in der ersten Grafik zu erkennen ist mit dem Frauenspagat mit dem rechten Bein vorne (FsARe) in der zweiten Grafik verglichen. Hierzu beziehen wir uns auf den aufgewärmten Zustand der Probanden.

Regressionsgleichung:

• FsALi = -17,12 + 0.4392 * Gew + 0.1651 * BeinlR
• FsARe = -11,74 + 0.4442 * Gew + 0.1008 * BeinlR

Die Ebenen für die beiden Frauenspagattypen sehen nahezu identisch aus. Das Gewicht ist jeweils als signifikant gekennzeichnet. Die Streuung ist beim Frauenspagat links niedriger als beim Frauenspagat rechts. Ebenso sind die p-Werte beim Frauenspagat rechts größer, was für einen kleineren Effekt der Variablen spricht.

Schritt 4: Auswertung der multiplen lienaren Regression

Auch wenn die einzelnen unabhängigen Variablen bei der linearen Regressionsanalyse signifikant waren, können wir bei der multiplen linearen Regression erkennen, dass manche Faktoren nicht mehr signifikant sind. Diese Variablen verlieren in Verbindung mit anderen Variablen ihren signifikanten Einfluss. Das heißt umso realitätsnäher unser Modell wird, desto größer ist die Wahrscheinlichkeit, dass mögliche Einflüsse nicht mehr signifikant sein können.

Ergebnisse der Modellbildungszyklen

Gesamtauswertung der Modellierungszyklen

Zyklus 1

Der erste Zyklus diente der Datenerhebung und der ersten Datenanalyse, mithilfe des Mittelwerts und der Boxplot Analyse. Die Ergebnisse gaben der Gruppe einen allgemeinen Überblick über Daten. Hier wurde festgestellt, dass eine große und gut verteilte Datenmenge nötig ist, um eine genaue Aussagen über die Faktoren, die die Höhe des Spagats beeinflussen, treffen zu können. Da der Gruppe dies in dem kurzen Zeitraum nicht möglich war, konnten sie nur Vermutungen über die Faktoren aufstellen:

• Als Frau ist der Abstand zum Boden in den verschiedenen Spagattypen geringer als beim Mann.
• Beim Frauenspagat erreicht jedes Geschlecht einen geringeren Abstand zum Boden, als beim Männerspagat.
• Aufgewärmte Personen kommen tiefer in den Spagat als Unaufgewärmte.

Zyklus 2

Die Zielsetzung von Zyklus II war es die aus Zyklus I erarbeiteten Variablen miteinander zu vergleichen und mögliche Korrelationen und Trends bezüglich der Spagattiefe zu entdecken, um damit dann mögliche Vorhersagen treffen zu können. Ebenso wurden Abweichungen der Daten, im Rahmen der Fehlerrechnung, berechnet. Die verwendeten mathematischen Methoden zur Datenanalyse waren die Korrelation nach Pearson, die Rangkorrelation nach Spearman, Lineare Regression und die Maximalfehlerabschätzung.

Zyklus 3

In diesem Zyklus sollte die Spagathöhe (Abstand zum Boden) als abhängige Variable unter dem Einfluss von zwei unabhängigen Variablen untersucht werden. Hierzu diente das Verfahren der multiplen linearen Regression, welche ein realitätnäheres Modell darstellt, als die lineare Regresssion. Hierzu mussten viele Voraussetzungen überprüft werden, damit das Modell einem signifikanten Erklärungsbeitrag leistet. Basierend auf unserer Datengrundlage war leider kein Modell signifikant. Trotzdem zeigten verschiedene Kombinationen von Variablen, dass postive oder negative Einflüsse bezüglich der Spagathöhe bestehen.

Grenzen des Modells

Grenzen der Modelierungsdurchführung

• Zeitliche Limitierung
• Finanzielle Limitierung

Mathematische Grenzen des Modells

• Visualisierungsgrenzen bei der Multiplen linearen Regression
• Die Mathematische Modellierung entspricht nicht der Realität. Zum Beispiel tragen nicht nur verschieden viele Faktoren zu einer gewissen Spagathöhe bei, sondern auch die jeweilige Kombination aus Faktoren und vielen individuellen und genetischen Einflussfaktoren, welche mathematisch nicht messbar sind

Sportwissenschaftliche Perspektive

Der Mensch ist ein sehr komplexes Lebenwesen. Sehr viele Faktoren bedingen sich gegenseitig, weshalb es sehr schwer ist ein klares Muster an Zusammenhängen zu erkennen. In unserem Fall haben wir uns hauptsächslich auf metrisch messbare Einflussfaktoren bezogen, da die Datenanalyse sonst schwer möglich ist. Im Alltag tritt somit die Linearität von Faktoren nur bedingt auf.

Mögliche Verbesserungen

Um das Thema zu Verbessern oder weiter ausbauen zu können, ist eine größere Stichprobe notwendig. Außerdem sollte man das Messintervall, besonders beim Alter, weiter eingrenzen um zum Beispiel über eine bestimmte Altersgruppe aussagekräftigere Ergebnisse über die Einflussfaktoren zu erhalten. Zusätzlich sollte bei jeder Analyse zwischen Männern und Frauen unterschieden werden, da die Faktoren wie Gewicht und Beinlänge sonst indirekt das Geschlecht berücksichtigen.

Außerdem könnte man das Spagattraining weiter unter die Lupe nehmen: Welche Technik ist am besten und welche Faktoren spielen hier eine besondere Rolle?

Aus medizinischer Sicht wäre es noch interessant zu Untersuchen, ob durch das Spagattraining das Einsetzen von künstlichen Hüftgelenken reduziert wird und ob die Beweglichkeit gefördert wird.