Kurs:Mathematische Modellbildung/Themen/Neuronales Netz/Modellierungszyklus Sekundarstufe I
Erscheinungsbild
Ziel
[Bearbeiten]- Allgemeiner Überblick über Biodiversität
- Grundlagen für Artenbestimmungen bieten
- Verdeutlichung der Ungenauigkeit von absoluten Artenanzahlen
- Probleme der Bestimmung und Zählungen verdeutlichen
- Umgang mit Dezimalzahlen
- Textanalyse
- Berechnungen des Mittelwerts
- Arbeiten mit Tabellenkalkulationsprogrammen →Erstellen, deuten
- Diagramme→ erstellen, lesen, interpretieren
Mathematische Theorie
[Bearbeiten]Mittelwert
[Bearbeiten]- Durchschnitt einer Menge von Zahlen
proportionaler Dreisatz
[Bearbeiten]- Lösungsverfahren, das aus mindestens zwei proportional zusammenhängenden Größen eine neue berechnet


Prozentrechnung
[Bearbeiten]- Verhältnis zweier Größen zueinander
- (1) Der Grundwert G ist die Ausgangsgröße = 100%
- (2) Der Prozentsatz p ist der Anteil des Grundwertes in %
- (3) Der Prozentwert W bezeichnet die Zahl, die den Anteil von G angibt
- Die zugehörige Formel lautet:
Diagramme erstellen
[Bearbeiten]- komplexe Daten analysieren, Muster, Trends oder Abweichungen auf einen Blick erkennen
- klare und prägnante Kommunikation von Informationen, unabhängig von Sprachbarrieren oder Fachkenntnissen
- erleichtern Entscheidungsfindung, indem sie komplexe Informationen vereinfachen, Beziehungen verdeutlichen und alternative Lösungen bewerten
- nutzen die visuelle Natur des Menschen, um Daten ansprechend zu präsentieren und Informationen besser im Gedächtnis zu behalten
- wertvolle Fähigkeit in verschiedenen beruflichen Bereichen und verbessert die Datenkompetenz sowie die Effektivität bei der Datenanalyse und -präsentation
Empirisches Gesetz der großen Zahlen
[Bearbeiten]- Führt man ein Zufallsexperiment oft aus, so stabilisieren sich die relativen Häufigkeiten rn(A) eines Ereignisses A um einen bestimmten Wert.
Bezug zum Rahmenlehrplan
[Bearbeiten]- L1 : Zahl und Zahlenbereieche
--> Prozentrechnung --> Bruchzahlen berechnen, vergleichen und ordnen
- L5: Daten und Zufall
--> Datenerhebung planen, durchführen und auswerten --> grafische Darstellungen interpretieren
Für den Modellierungszyklus der Sekundarstufe I können folgende Ziele den Unterricht strukturieren:
- Entwicklung grundlegender Vorstellungen des Prozentbegriffs
- Lösung von Grundaufgaben der Prozentrechnung, auch im Kopf
- Anwendung der Prozent- und Zinsrechnung in Sachsituationen
Modellierung
[Bearbeiten]Sichtungen Schüler in Tabellenkalkulation
[Bearbeiten]
Graphische Darstellung
[Bearbeiten]
Vergleich mit öffentlichen Daten
[Bearbeiten]- Sichtungen des Haussperlings im Schnitt in RLP: 6,17
- Sichtungen des Haussperlings im Schnitt in Landau in der Pfalz: 7,07
Entwicklung der Gartenvögel über die letzten 17 Jahren
[Bearbeiten]
Verbreitungskarten
[Bearbeiten]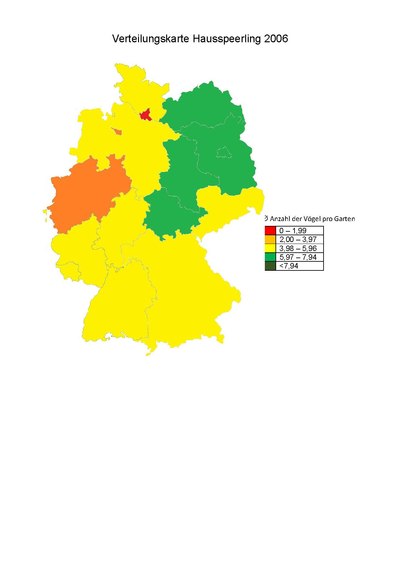
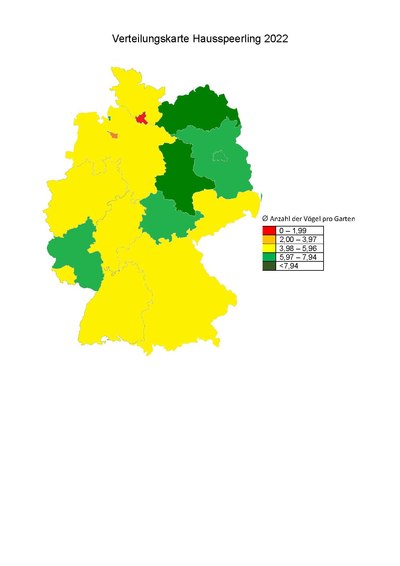
Prozentualer Anteil an Silbermöwen in Deutschland
[Bearbeiten]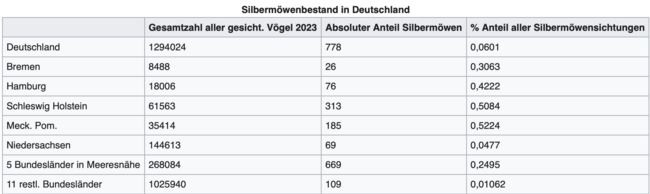
→85,98971 % der Sichtungen in Meeresnähe


Vereinfachung und Bewertung des Modellierungszyklus
[Bearbeiten]- Anpassung der Theorie je nach Klassenstufe
- Gesetz der großen Zahlen als zentrales Konzept
- Wichtige Aspekte bei der Modellierung: Herausforderungen bei der Zuordnung von Vogelarten, Einflussfaktoren auf die gezählten Sichtungen
- Genauigkeit der Daten begrenzt, Schüler sollen Realität von Daten erkennen
- Erstellung von Verbreitungskarten für Schüler von Klasse 5 bis 10 geeignet
- Untersuchung des prozentualen Anteils an Silbermöwen mit kleinerem Raster
- Mathematische Theorie ermöglicht Erforschung komplexer Themen und Herausforderungen bei Datenerfassung und -interpretation
- Optimierung der Ergebnisse durch gleiche Bedingungen bei Zählungen, Erweiterung der Stichprobe und Nutzung von Bildern, Stimmaufnahmen oder Videos zur Artenbestimmung
- Prognose für die Zukunft in Modellierungszyklus 2 mit genaueren Daten
- zur Beurteilung von Beobachtungen werden Größere Datensätze benötigt um Fehler zu minimieren
Warum Libre Calc
[Bearbeiten]- einfaches generieren von Zufallszahlen
- einfache Berechnung des Mittelwerts
- Übersichtliche tabellarische Darstellung
- Generieren von graphischen Darstellungen passend zur Tabelle
Warum GeoGebra
[Bearbeiten]- eigenständiges einzeichnen von einzelnen Punkten und Verbindungslinien
- einfache Handhabung auch für untere Klassenstufen


