Nullstellenbestimmung reeller Funktionen einer Veränderlichen
[Bearbeiten]Häufig sucht man in Anwendungen für eine gegebene stetige Funktion ![{\displaystyle f\in {\mathcal {C}}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/574d77a18b0a63187362202b74f55b9039f9b499) eine Nullstelle (auch Wurzel genannt), d. h. einen Punkt
eine Nullstelle (auch Wurzel genannt), d. h. einen Punkt  mit
mit  .
.
Weiß man zusätzlich, dass die Funktion 2x stetig differierbar ![{\displaystyle g\in {\mathcal {C}}^{2}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bc21aea0bf3108e60baae353083d0b466cb0928) ist, benötigt man für die Bestimmung der Extremalpunkte einer Funktion
ist, benötigt man für die Bestimmung der Extremalpunkte einer Funktion  die Nullstellen der 1. Ableitung und man setzt dazu
die Nullstellen der 1. Ableitung und man setzt dazu  und wendet auf
und wendet auf  das Nullstellenverfahren an. Mit der 2. Ableitung entscheidet man, ob ein Minimum oder Maximum vorliegt.
das Nullstellenverfahren an. Mit der 2. Ableitung entscheidet man, ob ein Minimum oder Maximum vorliegt.
Wurzeln mit Nullstellenverfahren bestimmen
[Bearbeiten]Wenn die Wurzel  für
für  näherungsweise bestimmen möchte, sucht man z.B. für nach der Nullstelle der Funktion
näherungsweise bestimmen möchte, sucht man z.B. für nach der Nullstelle der Funktion 
- in dem Intervall
![{\displaystyle [a,b]:=[1,c]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a407f507eabf9fd10a871d351da9af69d75e95f) für
für  und
und
- in dem Intervall
![{\displaystyle [a,b]:=[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/983c4dfae229d88532461943515a0cc9a1298089) für
für  .
.
Ein Fixpunkt ![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce) einer Funktion
einer Funktion ![{\displaystyle g:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b1d5103d0e36767a27715bcfc57137119294aad) ist ein Punkt mit der Eigenschaft
ist ein Punkt mit der Eigenschaft  , also dem Schnittpunkt des Graphen von
, also dem Schnittpunkt des Graphen von  mit der Winkelhalbierenden. Auch diese Problem kann man in ein Problem der Nullstellensuche überführen, indem man
mit der Winkelhalbierenden. Auch diese Problem kann man in ein Problem der Nullstellensuche überführen, indem man ![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac) über
über  definiert. Ein Fixpunkt von
definiert. Ein Fixpunkt von  ist damit eine Nullstelle von
ist damit eine Nullstelle von  .
.
- Analysieren die folgenden Nullstellenverfahren und berechnen Sie die Wurzel von 5 näherungsweise mit Tabellenkalkulation (LibreOffice).
- Definieren Sie eine Funktion
![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac) mit der man die 3. Wurzel aus
mit der man die 3. Wurzel aus  bestimmen kann.
bestimmen kann.
- Geben Sie eine Funktion
![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac) mit dem Intervall
mit dem Intervall ![{\displaystyle [a,b]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a659536067aaaac2db1c44613a09a715f0cf7246) an, wobei man mit Nullstellenverfahren die Stellen
an, wobei man mit Nullstellenverfahren die Stellen ![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce) näherungsweise bestimme kann, für die
näherungsweise bestimme kann, für die  gilt.
gilt.
Startintervall für Nullstellenverfahren
[Bearbeiten]Ist eine Funktion ![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac) gehen, so ist es im allgemeinen nicht notwendigerweise der Fall, dass
gehen, so ist es im allgemeinen nicht notwendigerweise der Fall, dass  gilt und damit eine Vorzeichenwechsel bei den Intervallrenzen vorliegt. In einem solchen Fall kann ggf. auf ein Teilintervall
gilt und damit eine Vorzeichenwechsel bei den Intervallrenzen vorliegt. In einem solchen Fall kann ggf. auf ein Teilintervall ![{\displaystyle [\alpha ,\beta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/878fce9eb3ba664f0ad4d025f04214fa85ee9583) in
in ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) übergehen, für das
übergehen, für das  .
.
Um eine möglichst gute Startnäherung für jede solche Nullstelle zu erhalten, sucht man dann Teilintervalle ![{\displaystyle [\alpha ,\beta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/878fce9eb3ba664f0ad4d025f04214fa85ee9583) in
in ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) , in dem ein Vorzeichenwechsel
, in dem ein Vorzeichenwechsel  vorliegt und möglichst nur eine Nullstelle
vorliegt und möglichst nur eine Nullstelle ![{\displaystyle x^{*}\in [\alpha ,\beta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f0d6f43e4635e2ea756d31f2ab81db9cd2a2f56) liegt.
liegt.
Zerlegung des Intervalls in Teilintervalle
[Bearbeiten]Dazu berechnet man im Allgemeinen Funktionswerte  mit
mit

für ein gegebenes, genügend großes  . Dadurch zerlegt man das Ausgangsintervall
. Dadurch zerlegt man das Ausgangsintervall ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) in
in  Teilintervalle und identifiziert die Teilintervalle in denen ein Vorzeichenwechsel vorliegt.
Teilintervalle und identifiziert die Teilintervalle in denen ein Vorzeichenwechsel vorliegt.
Die Menge aller  bezeichnet man auch als ein Gitter in
bezeichnet man auch als ein Gitter in ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) , die
, die  selbst als Gitterpunkte und den Prozess der Auswahl von endlich vielen Punkten aus
selbst als Gitterpunkte und den Prozess der Auswahl von endlich vielen Punkten aus ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) als Diskretisierung des Intervalls.
als Diskretisierung des Intervalls.
Sind  und
und  (anderenfalls hätte man eine Nullstelle von
(anderenfalls hätte man eine Nullstelle von  gefunden) und ist
gefunden) und ist

so muss  nach dem Zwischenwertsatz im Intervall
nach dem Zwischenwertsatz im Intervall ![{\displaystyle [\xi _{i},\xi _{i+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18e1c100697a48d4681971e1827d50908ac554a5) eine (einfache) Nullstelle besitzen und können wir
eine (einfache) Nullstelle besitzen und können wir  und
und  setzen.
setzen.
Anwendung unterschiedlicher Nullstellenverfahren
[Bearbeiten]Es werden im Folgenden eine Reihe von Verfahren behandelt, die, ausgehend von einem solchen Intervall mit Vorzeichenwechsel, unter geeigneten Bedingungen eine genäherte Nullstelle von  liefern. Dabei geht man davon aus, dass eine Funktion zumindest stetig ist, denn
liefern. Dabei geht man davon aus, dass eine Funktion zumindest stetig ist, denn ![{\displaystyle f\in {\mathcal {C}}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/574d77a18b0a63187362202b74f55b9039f9b499) liefert dem Zwischenwertsatz die Existenz einer Nullstelle
liefert dem Zwischenwertsatz die Existenz einer Nullstelle  mit
mit  . Für das Newtonverfahren benötigt man noch die zusätzliche Eigenschaft der Differenzierbarkeit, weil die Ableitung
. Für das Newtonverfahren benötigt man noch die zusätzliche Eigenschaft der Differenzierbarkeit, weil die Ableitung  für die Interation von
für die Interation von  zu
zu  benötigt wird.
benötigt wird.
Im Folgenden wird vorausgesetzt, dass  für
für ![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac) erfüllt ist.
erfüllt ist.
Das erste Verfahren, das wir vorstellen wollen, ist das Intervallschachtelungs- oder auch Bisektionsverfahren. Bei diesem wird, beginnend mit dem Intervall ![{\displaystyle [a_{0},b_{0}]\subseteq [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ff30ecec8b72bbdae52ac31fc85cb525c41e275) , eine Folge von Intervallen
, eine Folge von Intervallen ![{\displaystyle [a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13f59f1660676e1ffeb6e604b7011896c643a81d) erzeugt, so dass
erzeugt, so dass  und damit
und damit  gilt. Dieses Verfahren verwendet in jeder Iteration als einzige Information nur die Vorzeichen der Funktionswerte an den Randpunkten des aktuellen Intervalls, so dass keine schnelle Konvergenzgeschwindigkeit zu erwarten ist.
gilt. Dieses Verfahren verwendet in jeder Iteration als einzige Information nur die Vorzeichen der Funktionswerte an den Randpunkten des aktuellen Intervalls, so dass keine schnelle Konvergenzgeschwindigkeit zu erwarten ist.

- (0) Gib
![{\displaystyle a_{0},b_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73d04358f92a94d44da1c43598383bf757dd90f4) mit
mit  und
und  . Setze
. Setze  .
.
- (1) Berechne
 und
und  .
.
- (2) Falls
 , stop!
, stop!
- (3) Falls
 , setze
, setze  .
.
- Falls
 , setze
, setze  .
.
- (4) Setze
 und gehe nach (1).
und gehe nach (1).
Intervallbreite im Bisektionsverfahren
[Bearbeiten]Offenbar gilt für die Länge der bei der Bisektionsmethode erzeugten Intervalle ![{\displaystyle [a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13f59f1660676e1ffeb6e604b7011896c643a81d)

Wenn Algorithmus in Schritt (2) nicht abgebrochen wird, folgt damit

Wegen  sowie
sowie  oder
oder  hat man weiter mit der Abschätzung der Intervallbreite
hat man weiter mit der Abschätzung der Intervallbreite

und demnach

Bemerkung - Abbruchkriterium Bisektionsverfahren
[Bearbeiten]Die Abbruchbedingung (2)  schließt u.a. den Fall mit ein, dass
schließt u.a. den Fall mit ein, dass  gilt, also bei der Intervallmitte bereits die gesuchte Nullstelle gefunden wurde.
gilt, also bei der Intervallmitte bereits die gesuchte Nullstelle gefunden wurde.
Da  und
und  stetig ist, ist daher das Abbruchkriterium
stetig ist, ist daher das Abbruchkriterium  in Schritt (2) von Algorithmus nach endlich vielen Schritten erfüllt. Statt dieses Abbruchkriteriums, das beispielsweise im Fall
in Schritt (2) von Algorithmus nach endlich vielen Schritten erfüllt. Statt dieses Abbruchkriteriums, das beispielsweise im Fall
![{\displaystyle 0\leq f(x)\ll 1,\quad x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bba1d178ff1d7b09bc298c3f4ef0cfd2a490eb08)
ungünstig ist, könnte man alternativ oder zusätzlich auch die Abfrage  mit einer kleinen Konstante
mit einer kleinen Konstante  als
Abbruchkriterium verwenden.
als
Abbruchkriterium verwenden.
Beispiel - Genauigkeit Bisektionsverfahren
[Bearbeiten]Ist  , so folgt aus (5.6)
, so folgt aus (5.6)



Bemerkung - Konvergenzgeschwindigkeit und Stabilität
[Bearbeiten]Das Bisektionsverfahren ist ein sicheres und numerisch stabiles Verfahren, aber mit langsamer Konvergenz. Es konvergiert i. a. nicht einmal linear. Für die Fehler zweier aufeinander folgender Iterierter  und
und  kann sogar gelten:
kann sogar gelten:

Beispiel für Fehlervergrößerung in einem Iterationsschritt
[Bearbeiten]Für die Funktion  kann man die Nullstelle
kann man die Nullstelle  in
in ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) direkt angeben. Im Beispiel wird diese mit Bisektionsverfahren berechnet. Ferner ist
direkt angeben. Im Beispiel wird diese mit Bisektionsverfahren berechnet. Ferner ist  stetig und erfüllt
stetig und erfüllt  und
und  die Voraussetzung für die Anwendung des Bisektionsverfahrens:
die Voraussetzung für die Anwendung des Bisektionsverfahrens:
![{\displaystyle [a_{0},b_{0}]:=[-1,1],\quad x_{1}:=0,\quad f(x_{1})=0.1>0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ac04ac90f773d6e98169806737bfcc87ec5a744)
![{\displaystyle [a_{1},b_{1}]:=[-1,0],\quad x_{2}:=-0.5,\quad f(x_{2})=-0.4<0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52db422ead32d4c7945748294f4bd8135688eea7)
und demzufolge wird der Fehler von  zu
zu  größer:
größer:

Bei der Regula Falsi verwendet man im  -ten Schritt die Sekante, welche die Punkte
-ten Schritt die Sekante, welche die Punkte  und
und  verbindet. Diese Gerade kann durch Graph einer Funktion
verbindet. Diese Gerade kann durch Graph einer Funktion  dargestellt werden
dargestellt werden

Der Graph der  -ten Sekante
-ten Sekante  schneidet die
schneidet die  -Achse in dem folgenden Punkt:
-Achse in dem folgenden Punkt:

Der Punkt  wird nun als neue Näherung für
wird nun als neue Näherung für  genommen. Ansonsten verfährt man wie bei der Bisektion.
genommen. Ansonsten verfährt man wie bei der Bisektion.
Zeigen Sie, dass der Punkt  ein Nullstelle der Funktion
ein Nullstelle der Funktion ![{\displaystyle g_{k}:[a_{k},b_{k}]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cd1e5721d63a997ad1745dfe2ea24aa43d17e6c) ist.
ist.

Man startet mit einer stetigen Funktion ![{\displaystyle f:[a_{0},b_{0}]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f246baf7968b4e3ac0561d11db626e05b97646f7) , die auf dem Intervall
, die auf dem Intervall ![{\displaystyle [a_{0},b_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2838ee9034d5bf96adfb08ff6cc185c1aee56c18) einen Vorzeichenwechsel bei den Funktionswerten besitzt (d.h.
einen Vorzeichenwechsel bei den Funktionswerten besitzt (d.h.  ). Dann berechnet in jedem Iterationsschritt jeweils den Schnittpunkt der Sekante durch die Punkte
). Dann berechnet in jedem Iterationsschritt jeweils den Schnittpunkt der Sekante durch die Punkte  und
und  . Die Schnittpunkt teilt das Intervall
. Die Schnittpunkt teilt das Intervall ![{\displaystyle [a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13f59f1660676e1ffeb6e604b7011896c643a81d) in zwei Teilintervalle. Wenn
in zwei Teilintervalle. Wenn  gilt, hat man eine Nullstelle gefunden. Falls das
gilt, hat man eine Nullstelle gefunden. Falls das  , betrachtet man das Teilintervall
, betrachtet man das Teilintervall ![{\displaystyle [a_{k+1},b_{k+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60fbb3669535628fe816bec3d432cf054a45a063) in dem dann ein Vorzeichnenwechsel vorliegt.
in dem dann ein Vorzeichnenwechsel vorliegt.
- (0) Gib
![{\displaystyle a_{0},b_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73d04358f92a94d44da1c43598383bf757dd90f4) mit
mit  und
und  . Setze
. Setze  .
.
- (1) Berechne
 sowie
sowie  .
.
- (2) Falls
 , stop!
, stop!
- (3) Falls
 , setze
, setze  .
.
- Falls
 , setze
, setze  .
.
- (4) Setze
 und gehe nach (1).
und gehe nach (1).
Bemerkung - Abbruchkriterium Regula Falsi
[Bearbeiten]Die Abbruchbedingung (2)  schließt wieder den Fall mit ein, dass
schließt wieder den Fall mit ein, dass  gilt, also die Sekante durch die Punkte
gilt, also die Sekante durch die Punkte  die x-Achse bereits in der gesuchten Nullstelle schneidet.
die x-Achse bereits in der gesuchten Nullstelle schneidet.
Für die Regula Falsi ist keine aussagekräftige Fehlerabschätzung erhältlich. Aber sie konvergiert unter gewissen Voraussetzungen mindestens linear (siehe z. B. Stoer). Man beachte, dass wegen  keine Auslöschung bei der Berechnung von
keine Auslöschung bei der Berechnung von  eintritt, so dass das Verfahren überdies numerisch stabil ist. Die erzeugten Näherungen
eintritt, so dass das Verfahren überdies numerisch stabil ist. Die erzeugten Näherungen  liegen alle im Ausgangsintervall
liegen alle im Ausgangsintervall ![{\displaystyle [a_{0},b_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2838ee9034d5bf96adfb08ff6cc185c1aee56c18) und können alle auf einer Seite der gesuchten Nullstelle liegen.
und können alle auf einer Seite der gesuchten Nullstelle liegen.
Beim Sekantenverfahren wählt man, ähnlich wie bei der Regula Falsi, die Nullstelle einer Sekante als neue Iterierte, wobei jeweils die Sekante von den beiden letzten Iterationspunkten  und
und  des Graphen von
des Graphen von  verbunden werden. Der nächste Stelle
verbunden werden. Der nächste Stelle  der Iteration wieder der Schnittpunkt der Sekante
der Iteration wieder der Schnittpunkt der Sekante  mit der
mit der  -Achse, wenn dieser existiert.
-Achse, wenn dieser existiert.
Unterschiede - Regula Falsi und Sekantenverfahren
[Bearbeiten]- Bei Regula Falsi wird die Sekante zwischen den Punkten
 und
und  gebildet.
gebildet.
- Beim Sekantenverfahren wird die Sekante zwischen den beiden letzten Iterationspunkten
 und
und  des Graphen von
des Graphen von  gebildet.
gebildet.
Konsequenzen der Unterschiede - Regula Falsi und Sekantenverfahren
[Bearbeiten]- Bei Regula Falsi wird die Sekante in einem Teilintervall
![{\displaystyle [a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13f59f1660676e1ffeb6e604b7011896c643a81d) zwischen den Punkten
zwischen den Punkten  und
und  gebildet, in dem ein Vorzeichenwechsel
gebildet, in dem ein Vorzeichenwechsel  . Damit liegt die nachfolgende Iterationstelle
. Damit liegt die nachfolgende Iterationstelle  in dem Teilintervall
in dem Teilintervall ![{\displaystyle [a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13f59f1660676e1ffeb6e604b7011896c643a81d) .
.
- Beim Sekantenverfahren kann es möglich sein, dass die Sekantensteigung zwischen den beiden letzten Iterationspunkten
 und
und  so gering ist, dass der Schnittpunkt mit der
so gering ist, dass der Schnittpunkt mit der  -Achse außerhalb des Definitionsbereiches
-Achse außerhalb des Definitionsbereiches ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) liegt.
liegt.
- Im ungünstigen Fall, dass
 gilt, hat die Sekante sogar überhaupt keinen Schnittpunkt mit der
gilt, hat die Sekante sogar überhaupt keinen Schnittpunkt mit der  -Achse und das Verfahren bricht ab.
-Achse und das Verfahren bricht ab.
Wahl der Startwerte - Sekantenverfahren
[Bearbeiten]Im Allgemeinen kann man zwei Startstellen ![{\displaystyle x_{-1},x_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/579b88d1c09214efb899288ff6eb38ba31e8bfe0) wählen, die die Eigenschaft haben sollten, dass die zugehörige Sekante
wählen, die die Eigenschaft haben sollten, dass die zugehörige Sekante  eine Schnittpunkt mit der
eine Schnittpunkt mit der  -Achse in
-Achse in ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) besitzt. Dabei muss nicht notwendig
besitzt. Dabei muss nicht notwendig  gelten. Wenn allerdings die Voraussetzung
gelten. Wenn allerdings die Voraussetzung  erfüllt ist, so kann man analog zu Regula Falsi
erfüllt ist, so kann man analog zu Regula Falsi  und
und  wählen. In weiteren Iterationsschritten werden sich dann aber die Sekanten von Regula Falsi und dem Sekantenverfahren unterscheiden.
wählen. In weiteren Iterationsschritten werden sich dann aber die Sekanten von Regula Falsi und dem Sekantenverfahren unterscheiden.
Berechnung der Nullstelle der Sekanten
[Bearbeiten]Die Nullstelle der Sekante beim Sekantenverfahren ist offenbar durch

gegeben.

- (0) Gib
![{\displaystyle x_{-1},x_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/579b88d1c09214efb899288ff6eb38ba31e8bfe0) und
und  . Berechne
. Berechne  sowie
sowie  und setze
und setze  .
.
- (1) Berechne

- sowie
 .
.
- (2) Falls
 , stop!
, stop!
- (3) Setze
 und gehe nach (1).
und gehe nach (1).
Man beachte hier beim Sekantenverfahren in Schritt (1), dass man die Iterierte im  -ten Schritt eines Verfahrens meist als Korrektur der Iterierten im
-ten Schritt eines Verfahrens meist als Korrektur der Iterierten im  -ten Schritt schreibt, also in der Form
-ten Schritt schreibt, also in der Form  mit einem
mit einem  mit:
mit:

Bei Konvergenz des Verfahrens gegen  muss man
muss man  zumindest für größere
zumindest für größere  voraussetzen, dass also die Iterationsstellen genügend nahe bei der gesuchten Nullstelle
voraussetzen, dass also die Iterationsstellen genügend nahe bei der gesuchten Nullstelle  liegen.
liegen.
Während bei dem Bisektionsverfahren und der Regula Falsi die Konvergenz durch den Vorzeichenwechsel in dem jeweils betrachtet nächsten Teilintervall ![{\displaystyle [a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13f59f1660676e1ffeb6e604b7011896c643a81d) mit
mit ![{\displaystyle x_{k+1}\in [a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a96d094c556bcbbade0927a484efb3132711e975) und den sich immer weiter halbierende Intervallen sofort einleuchtet, ist das beim Sekantenverfahren nicht klar.
und den sich immer weiter halbierende Intervallen sofort einleuchtet, ist das beim Sekantenverfahren nicht klar.
Bei Regula Falsi wird die Sekante bzgl. der Intervallgrenzen von ![{\displaystyle [a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13f59f1660676e1ffeb6e604b7011896c643a81d) gebildet, was zu einer monoton steigenden Folge
gebildet, was zu einer monoton steigenden Folge  und einer monoton fallenden Folge
und einer monoton fallenden Folge  führt, die beide gegen die Nullstelle konvergieren
führt, die beide gegen die Nullstelle konvergieren  . Beim Sekantenverfahren weist die Folge der Iterationsstellen
. Beim Sekantenverfahren weist die Folge der Iterationsstellen  in der Regel kein Monotonieverhalten auf (weder steigend noch fallend)
in der Regel kein Monotonieverhalten auf (weder steigend noch fallend)
Auch der Fall
![{\displaystyle x_{k+1}\in [x_{k-1},x_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2d65c993b1d0fa388de1d4680f28f9c4faac026) bei
bei  bzw.
bzw.![{\displaystyle x_{k+1}\in [x_{k},x_{k-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9142c70a922026ee59a8a5adbf5c8e20a3e15fc6) bei
bei 
muss im Allgemeinen beim Sekantenverfahren nicht gelten, so dass das Verfahren im Allgemeinen nur lokal konvergiert. Genauer kann man den folgenden Satz beweisen (vgl. Isaacson and Keller[1]):
Unterschied zwischen Sekantenverfahren und Regula Falsi
[Bearbeiten]Bei der Anwendung des Sekantenverfahrens wird die Sekanten immer bzgl. der beiden vorhergehenden Iterationsstellen  und
und  gebildet und damit die nächste Iterationsstelle
gebildet und damit die nächste Iterationsstelle  berechnet, während bei der Regula Falsi die Sekante bzgl. der linken und rechten Intervallgrenze
berechnet, während bei der Regula Falsi die Sekante bzgl. der linken und rechten Intervallgrenze  bzw.
bzw.  gebildet wird, in dem ein Vorzeichenwechsel der stetigen Funktion zu finden ist.
gebildet wird, in dem ein Vorzeichenwechsel der stetigen Funktion zu finden ist.
Konsequenz der Unterschiede zwischen Sekantenverfahren und Regula Falsi
[Bearbeiten]Als Konsequenz der der Unterschiede zwischen Sekantenverfahren und Regula Falsi ergibt sich daher,
- dass bei der Regula Falsi der nächste Iterationspunkt
 immer im Intervall
immer im Intervall ![{\displaystyle [a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e30ce1f218c7164247ad32fbbcde76c02c817bd1) liegen muss,
liegen muss,
- dass bei dem Sekantenverfahren der Schnittpunkt der Sekante mit der
 -Achse nicht notwendigerweise zwischen
-Achse nicht notwendigerweise zwischen  und
und  liegen muss.
liegen muss.
Ferner ergeben sich auch Unterschiede in der Konvergenzgeschwindigkeit.
Sei ![{\displaystyle f\in {\mathcal {C}}^{2}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0851e7fb5e4bf3c491ec3b9aa3f70116010f3275) , und es existiere ein
, und es existiere ein ![{\displaystyle x^{*}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/653f569c55a45a11e1088a0d2209659611277c27) mit
mit  und
und  . Sind die Anfangsnäherungen
. Sind die Anfangsnäherungen  und
und  hinreichend nahe bei
hinreichend nahe bei  gewählt, so konvergiert nach Streichung des Abbruchkriterium in Schritt (2) durch das Sekantenverfahren erzeugte Folge
gewählt, so konvergiert nach Streichung des Abbruchkriterium in Schritt (2) durch das Sekantenverfahren erzeugte Folge  superlinear gegen
superlinear gegen  von der Ordnung
von der Ordnung  .
.
Bemerkung - Konvergenz Sekantenverfahren
[Bearbeiten]Das Sekantenverfahren konvergiert also im Allgemeinen schneller als das Bisektionsverfahren und die Regula Falsi. Anders als diese, neigt es aber zu instabilem Verhalten, da der Fall  und damit Auslöschung bei der Berechnung von
und damit Auslöschung bei der Berechnung von  eintreten kann.
eintreten kann.
Die schnelle Konvergenz des Sekantenverfahrens soll an einem Beispiel demonstriert werden.
Beispiel - Berechnung Wurzel 2 mit Sekantenverfahren
[Bearbeiten]Es soll  berechnet werden. Dies kann man tun, indem man die positive Nullstelle der Funktion
berechnet werden. Dies kann man tun, indem man die positive Nullstelle der Funktion  . Mit dem Startintervall
. Mit dem Startintervall ![{\displaystyle [a,b]:=[-2,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abd941b5a5d9f822d1a914249d8c183bbc60391f) sucht man die Nullstelle
sucht man die Nullstelle  und z.B. mit dem Startintervall
und z.B. mit dem Startintervall ![{\displaystyle [a,b]:=[0,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1321450d119150dacc4a354c4d7371778ad3e017) bestimmt man näherungsweise die Nullstelle
bestimmt man näherungsweise die Nullstelle  . In dem folgenden Beispiel setzen wir
. In dem folgenden Beispiel setzen wir ![{\displaystyle [a,b]:=[0,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1321450d119150dacc4a354c4d7371778ad3e017) .
.
Der gesuchte Wert lautet auf 12 Stellen hinter dem Dezimalpunkt genau

Vereinfachung der Interationsvorschrift
[Bearbeiten]Die Iterationsvorschrift des Sekantenverfahrens lässt sich hier durch Anwendung der 3. Binomischen Formel im Quotienten wie folgt vereinfachen:

Die Startstellen sollte nahe bei der gesuchten Nullstelle liegen und verwendet daher als Startstellen  und
und 
Man errechnet mit  und
und  für
für 

mit  und
und  für
für 

usw.
Insgesamt erhält man die Iteriertenfolge




wobei die richtigen Ziffern jeweils unterstrichen sind.
Hätte man mit der ursprünglichen Formel gearbeitet, wie man das meist in der Praxis zu tun hat, so hätte man 2 Funktionsauswertungen von  zur Berechnung von
zur Berechnung von  und jeweils eine für die von
und jeweils eine für die von  bis
bis  , d. h. insgesamt 5 Funktionsauswertungen zur Berechnung von
, d. h. insgesamt 5 Funktionsauswertungen zur Berechnung von  benötigt.
benötigt.
Funktionsauswertungen sind in vielen Situationen ein gutes praktisches Vergleichskriterium für unterschiedliche Algorithmen zur Lösung eines Problems, da diese häufig die numerisch teuersten Teilaufgaben bei der Problemlösung darstellen.
Es sei nun ![{\displaystyle f\in {\mathcal {C}}^{1}[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9507efe3d8755c5daac928da5fef46814b664d87) und die Existenz eines
und die Existenz eines  mit
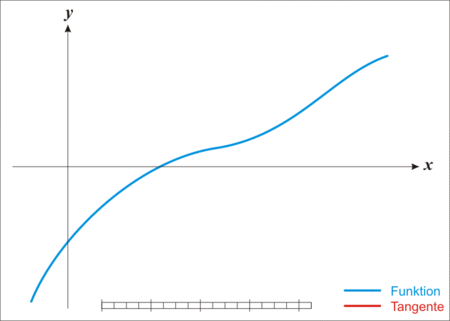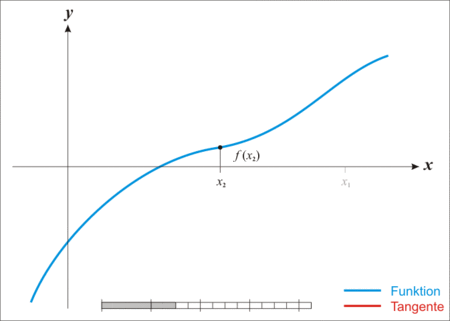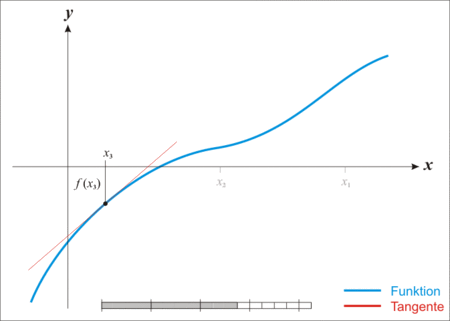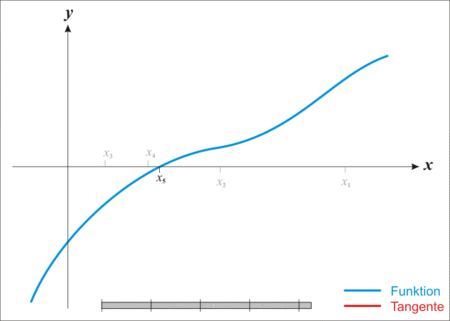
mit  vorausgesetzt. Beim Newton-Verfahren benötigt man nur eine Startnäherung
vorausgesetzt. Beim Newton-Verfahren benötigt man nur eine Startnäherung  für
für  . Ist
. Ist  die Näherung für
die Näherung für  zu Beginn der
zu Beginn der  -ten Iteration, so wählt man bei diesem Verfahren die Nullstelle
-ten Iteration, so wählt man bei diesem Verfahren die Nullstelle  der Tangente im Punkt
der Tangente im Punkt  an den Graphen von
an den Graphen von  als nächste Näherung.
als nächste Näherung.
Die Funktion ![{\displaystyle g_{k}\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad25571dac733bab9efda340794e557ebfa13d3e) , dessen Graph die Tangente in
, dessen Graph die Tangente in ![{\displaystyle x_{k}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/106ca6612536b72829ef241cdae4b90c90be51f6) beschreibt, wird wie folgt definiert:
beschreibt, wird wie folgt definiert:

gegeben, so dass man  für folgendes
für folgendes  erfüllt ist:
erfüllt ist:

erhält.
- Erläutern Sie an einem Schaubild/Zeichnung die Herleitung des Funktionsterms von
 !
!
- Erläutern Sie an einem eigenzeichnet Steigungsdreieck in einer Skizze die geometrische Herleitung des Terms
 !
!
Bemerkung - Eigenschaft der Ableitung an der gesuchten Nullstelle
[Bearbeiten]Wenn wir beispielsweise  voraussetzen (
voraussetzen ( ist dann eine einfache Nullstelle), können wir dabei zumindest für solche
ist dann eine einfache Nullstelle), können wir dabei zumindest für solche  , die nahe bei
, die nahe bei  liegen,
liegen,  annehmen. Wenn die Ableitung stetig ist, gibt es eine Umgebung
annehmen. Wenn die Ableitung stetig ist, gibt es eine Umgebung  , in der
, in der  nur positiv (streng monoton steigend) oder nur negativ ist (streng monoton fallend).
nur positiv (streng monoton steigend) oder nur negativ ist (streng monoton fallend).
Abgebraische und geometrische Konsequenzen von f'(x)=0
[Bearbeiten]- (Algebra) Wenn man sich die Iterationsvorschrift vom Newtonverfahren ansieht, führt
 im Nenner zu einem undefinierten Iterationsschritt für die Definition von
im Nenner zu einem undefinierten Iterationsschritt für die Definition von  .
.
- (Geometrie) Im Fall
 und
und  hätte die Tangente als Parallele zur
hätte die Tangente als Parallele zur  -Achse auch keine Nullstelle, wobei das Newton-Verfahren keine nächste Iterationsstelle liefert.
-Achse auch keine Nullstelle, wobei das Newton-Verfahren keine nächste Iterationsstelle liefert.
- (0) Wähle ein
 und
und  , berechne
, berechne  und setze
und setze  .
.
- (1) Berechne
 ,
,
- (5.9)

- und
 .
.
- (2) Falls
 , stop!
, stop!
- (3) Setze
 und gehe nach (1).
und gehe nach (1).
Beispiel - Newton-Verfahren zur Berechnung der Wurzel 2
[Bearbeiten]Man betrachtet nun eine Funktion ![{\displaystyle f:[1,2]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ce45064f6ef30e9c581df7e8ca0d477ecf4f7c1) mit dem Funktionsterm
mit dem Funktionsterm  und damit ist
und damit ist  . Gesucht ist die positive Nullstelle
. Gesucht ist die positive Nullstelle  von
von  .
.
Die Iterationsvorschrift des Newton-Verfahrens lässt sich hier schreiben als

Beginnend mit ![{\displaystyle x_{0}:=1.5\in [1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6771677fa26aca5c5042c3c7b10533fcdb32e69f) und
und  berechnet man die Iterierten
berechnet man die Iterierten



Die unterstrichen Ziffern nach dem Iterationsschritt bezeichnen, wie viele Stelle bereits mit der gesuchten Nullstelle von  übereinstimmen
übereinstimmen
Bei direkter Verwendung von der allgemeinen Iterationsvorschrift

muss man für jeden Iterationsschritt neben Division und Subtraktion einmal  und einmal
und einmal  auswerten.
Das wären für die Berechnung von
auswerten.
Das wären für die Berechnung von  jeweils 3 Funktionsauswertungen von
jeweils 3 Funktionsauswertungen von  und
und  , also insgesamt 6 Funktionsauswertungen erforderlich gewesen. Das Newtonverfahren ist also in diesem Fall ein sehr schnelles Verfahren.
, also insgesamt 6 Funktionsauswertungen erforderlich gewesen. Das Newtonverfahren ist also in diesem Fall ein sehr schnelles Verfahren.
Vergleich mit Sekantenverfahren im Beispiel
[Bearbeiten]Bei diesem Beispiel  und der Wahl von Startwerten (!) erreicht das Sekantenverfahren aber mit etwas weniger Aufwand sogar etwas höhere Genauigkeit.
und der Wahl von Startwerten (!) erreicht das Sekantenverfahren aber mit etwas weniger Aufwand sogar etwas höhere Genauigkeit.
Wir wollen uns nun mit der Konvergenz des Newton-Verfahrens beschäftigen. Dazu holen wir etwas weiter aus. Für eine gegebene Funktion  nennen wir einen Punkt
nennen wir einen Punkt  mit
mit

einen Fixpunkt von  . Weiter sprechen wir bei der Iterationsvorschrift
. Weiter sprechen wir bei der Iterationsvorschrift

von der Fixpunktiteration mit der Verfahrensfunktion  . Ist
. Ist  stetig und konvergiert die Iteriertenfolge, so muss ihr Grenzwert offenbar notwendig ein Fixpunkt von
stetig und konvergiert die Iteriertenfolge, so muss ihr Grenzwert offenbar notwendig ein Fixpunkt von  sein. Man beachte in diesem Zusammenhang, dass
sein. Man beachte in diesem Zusammenhang, dass  genau dann Fixpunkt von
genau dann Fixpunkt von  ist, wenn
ist, wenn  Nullstelle z. B. der Funktion
Nullstelle z. B. der Funktion  ist, dass also die Probleme der Bestimmung einer Nullstelle und der eines Fixpunktes einer Funktion äquivalent sind.
ist, dass also die Probleme der Bestimmung einer Nullstelle und der eines Fixpunktes einer Funktion äquivalent sind.
Wir beweisen nun folgenden allgemeinen Satz über die lokale Konvergenz der Fixpunktiteration, wobei

eine offene  -Umgebung des Punktes
-Umgebung des Punktes  bezeichne.
bezeichne.
Sei  gegeben und
gegeben und  Fixpunkt von
Fixpunkt von  . Weiter sei
. Weiter sei  in
in 
 -mal differenzierbar mit einem
-mal differenzierbar mit einem  , und es gelte entweder
, und es gelte entweder
 für
für  oder
oder für
für 
Dann existiert ein  , so dass die durch
, so dass die durch  erzeugte Iteriertenfolge
erzeugte Iteriertenfolge  für jeden Startpunkt
für jeden Startpunkt  gegen
gegen  konvergiert und zwar mindestens von der Ordnung
konvergiert und zwar mindestens von der Ordnung  . Im Fall
. Im Fall  ist die Konvergenzordnung genau
ist die Konvergenzordnung genau  .
.
Beweis - Konvergenzsatz - Fixpunktiteration
[Bearbeiten]Taylorentwicklung von  um
um  liefert für beide Fälle in (5.10)
liefert für beide Fälle in (5.10)

 für
für 
Somit hat man
- (5.11)

so dass zu einem gegebenen  ein
ein  existiert und
existiert und

- (5.12)
![{\displaystyle =\left[C|x-x^{*}|^{p-1}\right]|x-x^{*}|={\tilde {C}}(x)|x-x^{*}|,\quad x\in {\mathcal {U}}_{\delta }(x^{*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e58834a9d47ac6dc3957e2caf24266cd247b2c40)
mit  und
und  gilt. Im Fall
gilt. Im Fall  sei dabei
sei dabei  so klein gewählt, dass
so klein gewählt, dass

ist, was aufgrund der Voraussetzung  möglich ist. Für
möglich ist. Für  ist es offenbar möglich,
ist es offenbar möglich,  so klein zu wählen, dass
so klein zu wählen, dass  für alle
für alle  folgt.
folgt.
Die Ungleichung (5.12) impliziert nun für  auch
auch  und damit im Fall
und damit im Fall  auch
auch  für alle
für alle  , so dass man
, so dass man

hat und daraus wegen  die Konvergenz
die Konvergenz  von mindestens der Ordnung
von mindestens der Ordnung  schließen kann. Ist die Zusatzbedingung
schließen kann. Ist die Zusatzbedingung  erfüllt und wird oben
erfüllt und wird oben  so gewählt, dass
so gewählt, dass  gilt, so gilt wegen (5.11)
gilt, so gilt wegen (5.11)
- (5.13)

Daraus folgt die genaue Konvergenzordnung  in diesem Fall, denn wäre diese mindestens
in diesem Fall, denn wäre diese mindestens  , so folgte mit (5.13) für ein
, so folgte mit (5.13) für ein  und ein
und ein 

und damit im Widerspruch zu Konvergenz von  gegen
gegen 

q.e.d.
In dem folgenden Satz wird nun unter verschiedenen Voraussetzungen eine jeweilige Konvergenzordnung des Newton-Verfahrens angegeben.
Es sei  gegeben und es existiere
gegeben und es existiere  mit
mit  . Mit einem
. Mit einem  sei weiter für Aussage (i)
sei weiter für Aussage (i)  und für Aussage (ii)
und für Aussage (ii)  . Dann gilt nach Streichung von Schritt (2) für die durch das Newton-Verfahren (Algorithmus 8) erzeugte Folge
. Dann gilt nach Streichung von Schritt (2) für die durch das Newton-Verfahren (Algorithmus 8) erzeugte Folge  :
:
- (i) Ist
 , dann existiert ein
, dann existiert ein ![{\displaystyle \delta \in (0,\eta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/477b0dff5329264802730305bce276edaba0ce7e) , so dass
, so dass  für jeden Startpunkt
für jeden Startpunkt  gegen
gegen  konvergiert und zwar mindestens quadratisch. Im Fall
konvergiert und zwar mindestens quadratisch. Im Fall  konvergiert
konvergiert  sogar von einer Ordnung
sogar von einer Ordnung  .
.
- (ii) Ist
 andererseits eine
andererseits eine  -fache Nullstelle von
-fache Nullstelle von  mit einem
mit einem  , d. h., ist
, d. h., ist

- und ist weiter
 in
in  zweimal differenzierbar, so ist die Iterationsfunktion
zweimal differenzierbar, so ist die Iterationsfunktion
- (5.14)

des Newton-Verfahrens differenzierbar in  mit
(5.15)
mit
(5.15)  und existiert ein
und existiert ein ![{\displaystyle \delta \in (0,\eta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/477b0dff5329264802730305bce276edaba0ce7e) , so dass
, so dass  für jeden Startpunkt
für jeden Startpunkt  (genau) linear gegen
(genau) linear gegen  konvergiert.
konvergiert.
Die Behauptung folgt mit Satz 5.9, wenn man diesen auf  in (5.14) anwendet sowie mit den folgenden Darstellungen. Im Fall (i) zeigt man zunächst die Stetigkeit von
in (5.14) anwendet sowie mit den folgenden Darstellungen. Im Fall (i) zeigt man zunächst die Stetigkeit von  und
und  in
in  . Man ermittelt dann
. Man ermittelt dann

so dass also

gilt. Damit folgt die Behauptung.
Im Fall (ii) erhält man

und somit
- (5.16)

Wegen  folgt damit
folgt damit  und ist demzufolge
und ist demzufolge  aus (5.14) stetig in
aus (5.14) stetig in  . Weiter hat man mit (5.16) wegen
. Weiter hat man mit (5.16) wegen 

![{\displaystyle =1-\lim _{h\to 0}{\frac {hz(x^{*}+h)}{h[mz(x^{*}+h)+hz'(x^{*}+h)]}}=1-{\frac {1}{m}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ca650da5666153643061161b75d081bd3e505b9)
Also ist  und damit insbesondere auch
und damit insbesondere auch  .
.
q.e.d.
Man beachte, dass das Newton-Verfahren pro Iteration zwei Funktionsauswertungen benötigt, während das Sekanten-Verfahren nur eine verlangt. Im Fall, dass der Grenzwert eine einfache Nullstelle ist, konvergiert letzteres Verfahren unter geeigneten Voraussetzungen aber nur superlinear, während das Newton-Verfahren dann mindestens quadratisch konvergiert. Es stellt sich also die Frage, welches der Verfahren in der Praxis effizienter ist. Bemerkenswert ist es daher, dass man zeigen kann, dass das Sekantenverfahren, wenn man zwei Iterationen zu einer zusammenfasst und es damit etwa gleichen Aufwand pro Iteration wie das Newton-Verfahren bekommt, eine Konvergenzrate von mindestens  hat, und es folglich lokal schneller als das Newton-Verfahren konvergiert. Allerdings neigt das Sekanten-Verfahren, anders als das Newton-Verfahren, aufgrund von Auslöschungen zu instabilem Verhalten.
hat, und es folglich lokal schneller als das Newton-Verfahren konvergiert. Allerdings neigt das Sekanten-Verfahren, anders als das Newton-Verfahren, aufgrund von Auslöschungen zu instabilem Verhalten.
- ↑ Isaarcson E., Bishop Keller, H. (1966) Analysis of Numerical Methods, Wiley Sons URL: https://vdocument.in/isaacson-keller-analysis-of-numerical-methods.html?page=1
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Numerik I' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

![{\displaystyle f\in {\mathcal {C}}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/574d77a18b0a63187362202b74f55b9039f9b499)


![{\displaystyle g\in {\mathcal {C}}^{2}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bc21aea0bf3108e60baae353083d0b466cb0928)






![{\displaystyle [a,b]:=[1,c]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a407f507eabf9fd10a871d351da9af69d75e95f)

![{\displaystyle [a,b]:=[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/983c4dfae229d88532461943515a0cc9a1298089)

![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)
![{\displaystyle g:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b1d5103d0e36767a27715bcfc57137119294aad)

![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)


![{\displaystyle [a,b]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a659536067aaaac2db1c44613a09a715f0cf7246)


![{\displaystyle [\alpha ,\beta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/878fce9eb3ba664f0ad4d025f04214fa85ee9583)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle x^{*}\in [\alpha ,\beta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f0d6f43e4635e2ea756d31f2ab81db9cd2a2f56)








![{\displaystyle [\xi _{i},\xi _{i+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18e1c100697a48d4681971e1827d50908ac554a5)





![{\displaystyle [a_{0},b_{0}]\subseteq [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ff30ecec8b72bbdae52ac31fc85cb525c41e275)
![{\displaystyle [a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13f59f1660676e1ffeb6e604b7011896c643a81d)


![{\displaystyle a_{0},b_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73d04358f92a94d44da1c43598383bf757dd90f4)



















![{\displaystyle 0\leq f(x)\ll 1,\quad x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bba1d178ff1d7b09bc298c3f4ef0cfd2a490eb08)











![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)


![{\displaystyle [a_{0},b_{0}]:=[-1,1],\quad x_{1}:=0,\quad f(x_{1})=0.1>0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ac04ac90f773d6e98169806737bfcc87ec5a744)
![{\displaystyle [a_{1},b_{1}]:=[-1,0],\quad x_{2}:=-0.5,\quad f(x_{2})=-0.4<0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52db422ead32d4c7945748294f4bd8135688eea7)













![{\displaystyle g_{k}:[a_{k},b_{k}]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cd1e5721d63a997ad1745dfe2ea24aa43d17e6c)

![{\displaystyle f:[a_{0},b_{0}]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f246baf7968b4e3ac0561d11db626e05b97646f7)
![{\displaystyle [a_{0},b_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2838ee9034d5bf96adfb08ff6cc185c1aee56c18)

![{\displaystyle [a_{k+1},b_{k+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60fbb3669535628fe816bec3d432cf054a45a063)






![{\displaystyle x_{-1},x_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/579b88d1c09214efb899288ff6eb38ba31e8bfe0)














![{\displaystyle x_{k+1}\in [a_{k},b_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a96d094c556bcbbade0927a484efb3132711e975)



![{\displaystyle x_{k+1}\in [x_{k-1},x_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2d65c993b1d0fa388de1d4680f28f9c4faac026)

![{\displaystyle x_{k+1}\in [x_{k},x_{k-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9142c70a922026ee59a8a5adbf5c8e20a3e15fc6)




![{\displaystyle [a_{n},b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e30ce1f218c7164247ad32fbbcde76c02c817bd1)

![{\displaystyle f\in {\mathcal {C}}^{2}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0851e7fb5e4bf3c491ec3b9aa3f70116010f3275)
![{\displaystyle x^{*}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/653f569c55a45a11e1088a0d2209659611277c27)








![{\displaystyle [a,b]:=[-2,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abd941b5a5d9f822d1a914249d8c183bbc60391f)

![{\displaystyle [a,b]:=[0,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1321450d119150dacc4a354c4d7371778ad3e017)















![{\displaystyle f\in {\mathcal {C}}^{1}[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9507efe3d8755c5daac928da5fef46814b664d87)

![{\displaystyle g_{k}\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad25571dac733bab9efda340794e557ebfa13d3e)
![{\displaystyle x_{k}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/106ca6612536b72829ef241cdae4b90c90be51f6)











![{\displaystyle f:[1,2]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ce45064f6ef30e9c581df7e8ca0d477ecf4f7c1)



![{\displaystyle x_{0}:=1.5\in [1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6771677fa26aca5c5042c3c7b10533fcdb32e69f)




























![{\displaystyle =\left[C|x-x^{*}|^{p-1}\right]|x-x^{*}|={\tilde {C}}(x)|x-x^{*}|,\quad x\in {\mathcal {U}}_{\delta }(x^{*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e58834a9d47ac6dc3957e2caf24266cd247b2c40)



























![{\displaystyle \delta \in (0,\eta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/477b0dff5329264802730305bce276edaba0ce7e)
















![{\displaystyle =1-\lim _{h\to 0}{\frac {hz(x^{*}+h)}{h[mz(x^{*}+h)+hz'(x^{*}+h)]}}=1-{\frac {1}{m}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ca650da5666153643061161b75d081bd3e505b9)


