Kurs:Räumliche Modellbildung/Gruppe 9
Gruppenseite - HP
[Bearbeiten]Diese Seite enthält die gesammelten Materialien der Gruppe 9 - VN für die Portfolioprüfung.
Teilnehmer-innen
[Bearbeiten]- Mezler, Erika
- Schäfer, Erik
- Dörr, Moritz
- Möhle, Kristin
Einordnung des Themas
[Bearbeiten]

Dieses Portfolio versucht sich an der mathematischen Modellierung der Verbreitung des Erregers der COVID-19 Erkrankung, SARS-CoV-2 (Severe acute respiratory syndrome coronavirus type 2) im Rahmen des Moduls 11 des Studiengangs Master of Education im Fach Mathematik.[1]
Sustainable Development Goals
[Bearbeiten]Die 17 Ziele für nachhaltige Entwicklung (englisch Sustainable Development Goals, SDGs) sind politische Zielsetzungen der Vereinten Nationen (UN), die auf Grundlage der Millenniums-Entwicklungsziele (MDGs) entworfen wurden und am 1. Januar 2016 mit einer Laufzeit von 15 Jahren, also bis zum Jahr 2030, in Kraft traten. Sie streben eine weltweite Sicherung nachhaltiger Entwicklung an.
- Ziel 3: Gesundes Leben für alle – ein gesundes Leben für alle Menschen jeden Alters gewährleisten und ihr Wohlergehen fördern[2]
- Ziel 13: Sofortmaßnahmen ergreifen, um den Klimawandel und seine Auswirkungen zu bekämpfen[3]
- Ziel 17: Umsetzungsmittel und globale Partnerschaft stärken – Umsetzungsmittel stärken und die globale Partnerschaft für nachhaltige Entwicklung mit neuem Leben füllen[4]
Zoonosen sind Krankheiten, bei denen der Erreger von Tieren übergesprungen ist. Darunter zählen unter anderem das Ebola-Virus (Zaire und Sudan, 1976), HIV/Aids-Virus (USA, ab 1981), die Vogelgrippe H5N1 (Hongkong, 1997) und Mers (Saudi-Arabien, 2012)[5]. Diese Krankheiten haben Epidemien bzw. Pandemien ausgelöst, teilweise mit Millionen Todesopfern. Auf die Frage, ob es bald neue Pandemie geben werde, antwortet der Virologe und Leiter Berliner Charité Christian Drosten: "Die Tierhaltung bietet ideale Bedingungen für ein Virus, um sich an den Menschen anzupassen. (...) Eine Wachsende Menschheit mit einem wachsenden Fleischhunger: Hier steckt das Risiko für künftige Pandemien."[6]. Doch auch die Abholzung von tropischen Regenwäldern und die damit verbundenen Zerstörung von Lebensraum können potentielle Zoonosen bei ihrer Verbreitung begünstigen. Unter Berücksichtigung der SDGs 3 und 13 lässt sich somit ein enger Zusammenhang zwischen dem Schutz des Klimas und der Gesundheit aller Menschen erkennen, oder mit anderen Worten: Klimaschutz ist Gesundheitsschutz.
Zeitlicher Überblick der Coronavirus-Pandemie
[Bearbeiten]30.12.2019: China meldet der WHO eine bisher unbekannte Lungenkrankheit
23.01.2020: Die chinesische Millionenstadt Wuhan wird abgeriegelt
27.01.2020: Erster Fall in Deutschland
16.03.2020: Schließung der Schulen in Deutschland
22.03.2020: Erster Lockdown in Deutschland mit Kontaktverboten
07.09.2020: Die Zahl der kumulierten Infizierten überschreitet die 500.000-Marke
28.10.2020: Bund und Länder beschließen einen "Lockdown light", der am 02.11. in Kraft tritt
13.11.2020: Die 7-Tage-Inzidenz erreicht ihren vorläufigen Höchsttand: 158,7
12.12.2020: Bund und Länder beschließen einen harten Lockdown, der am 16.12. in Kraft tritt
23.12.2020: Die 7-Tage-Inzidenz erreicht ihren vorläufigen Höchststand: 217,3
27.12.2020: Impfstart in Deutschland
15.01.2021: Die Zahl der kumulierten Infizierten überschreitet die 2.000.000-Marke
06.04.2021: Hausärzte starten Impfungen
21.04.2021: Bundesnotbremse, u.a. mit Ausgangssperren
07.06.2021: Impfpriorisierungen fallen
Juni 2021: Die Delta-Variante breitet sich in Deutschland aus.
23.08.2021: Die Hospitalisierungsrate wird neue Kennzahl der Pandemie.
Diskrete und kontinuierliche Modellierung
[Bearbeiten](vgl. hierzu Pauer, Franz und Stampfer, Florian: [7]) Mathematische Modellierung stellt einer der drei allgemeinen mathematischen Kompetenzen der Bildungsstandards. Darin heißt es:

"(Mathematisch) Modellieren bedeutet, einen Sachverhalt, einen VOrgang, einen Zusammenhang, ... durch Begriffe der Mathematik zu beschreiben. [...] Warum wird mathematisch modelliert? Man hofft, damit eine Fragestellung zur betrachteten Situation mit Hilfe mathematischer Methoden zumindest näherungsweise beantworten zu können."[8]
Dabei kann man unterschiedlich vorgehen. "Die Unterscheidung von Diskretem (Lat. discrētus =abgesondert, getrennt) und Kontinuierlichem (Lat.continuus = zusammenhängend) ist fast so alt wie die Mathematik selbst. Bereits die griechische Antike teilt die Mathematik, die Wissenschaft von den Größen, in diesem Sinne in zwei Bereiche ein: Mathematik ist zum einen Arithmetik, die Lehre von den diskreten Größen, also den Zahlen und zum anderen Geometrie, die Lehre von den kontinuierlichen Größen, also den Figuren in der Ebene oder im dreidimensionalen Raum."[9] Im Rahmen dieser Arbeit betrachtet man die aktuelle Corona-Situation von beiden Seiten: einmal wird ein diskretes und einmal ein kontinuierliches Modell angefertigt:
- Eine Situation diskret zu modellieren bedeutet, dass sie durch eine Funktion beschrieben wird, deren Definitionsbereich eine endliche Menge ist und die häfig eine Folge als Lösung einer Differenzengleichung hat.
- Dagegen bedeutet es eine Situation kontinuierlich zu modllieren, dass sie durch eine Funktion beschrieben wird, deren Definitionsbereich ein reeles Intervall ist. Häufig ist diese Funktion differenzierbar und die Lösung einer Differenzialgleichung.
Kontinuierliche Modellierung
[Bearbeiten]Tutoriumsaufgabe 1: Kontaktmodell
[Bearbeiten]Als erstes räumliches Modell wird das intuitive Deterministische Kontaktmodell betrachtet: Das Grundprinzip ist recht einfach: Zu Beginn werden Punkte, die die verschiedenen Individuen darstellen, gleichmäßig verteilt. Ab einem Zeitpunkt bewegen sich diese mit einer konstanten Geschwindigkeit in eine zufällig gewählte, aber feste Richtung. Zu Beginn ist ein Individuum (zunächst in der Mitte) infiziert. Dieser sei rot markiert. Sobald sich der infizierte Punkt einem anderen derart annähert, dass ein gewisser, festgelegter Abstand (Infektionsradius) unterschritten wird, so wird dieser Punkt ebenfalls infiziert. Dabei wirken sich verschiedene Faktoren, wie die Geschwindigkeit , die Position des Infizierten, etc unterschiedlich auf die Ausbreitung der Infizierung aus. Vorwegs sei anzumerken, dass das Modell die Realität nur stark eingeschränkt abbildet, da Infektionen keine deterministischen Prozesse sind. So kann beispielsweise ein Individuum nach einer Infektion nicht genesen. Insofern ist es ein gutes Modell, um die Ausbreitung einer Infektion zu visualisieren, nicht aber, um die Realität abzubilden.
Theoretische Grundlagen
[Bearbeiten]Das deterministische Kontaktmodell basiert darauf, dass eine Infektion nur dann erfolgt, sobald eine festgelegte Abstandsschranke unterschritten wurde. Der Abstand wird dabei anhand eines metrischen Raums bestimmt. Hierfür wird zunächst eine Abbildung auf der Menge der Person/Individuen definiert, die jeder Person den epidemiologischen Status zuordnet.
Ferner befindet sich ein infiziertes Individuum an dem Ort und eine empfängliche Person an dem Ort . Betrachtet man als Kontaktdistanzschranke für die Infektion und seien , dann infiziert die Person unter folgender Bedingung:
Zusammengefasst: Durch das Kontaktmodell wird die mögliche räumliche Ausbreitung einer Infektion durch den Kontakt von sich bewegenden Individuen innerhalb eines sogenannten Infektionsradius beschrieben. Sobald ein gewisser Mindestabstand unterschritten wurde, erfolgt eine Infizierung.
Konstruktion der statischen Matrix
[Bearbeiten]In einem ersten Schritt wird ein 20x10 Punktgitter erzeugt. Jeder Punkt steht dabei für ein (noch unbewegtes) Individuum innerhalb der Matrix:
Nx=20; %Anzahl der Punkte in x-Richtung Ny=10; %Anzahl der Punkte in y-Richtung x=[1:Nx]; %erstellt Koordinaten-Vektoren der Punkte y=[1:Ny]; %erstellt Koordinaten-Vektoren der Punkte [x,y]=meshgrid (x,y) %erzeugt das Punktgitter

Mit dem nachfolgendem Befehl können wir uns diese Matrix als eine Grafik ausgeben lassen:
figure (1) hold on; plot(x,y, '*b') ; axis([-5 25 -5 15); hold off;
Das erste infizierte Individuum
[Bearbeiten]Weiter folgt die Generierung des ersten infizierten Individuums. Der Einfachheit halber setzen wir diesen genau in die Mitte unserer Matrix.
xInf=x(1, Nx/2); %Position in x-Richtung yInf=y(Ny/2); %Position in y-Richtung IndInf2=Nx/2; %Spalte IndInf1=Ny/2; %Zeile IndInf1neu=IndInf1; IndInf2neu=IndInf2; close all;

Dies lassen wir erneut als Grafik ausgeben:
figure (2) hold on; plot(x,y, '*b') ; plot(xInf,yInf, 'sr') ; axis([-5 25 -5 15]); hold off;

Selbstverständlich kann die Position des ersten infizierten Individuums variiert werden. So zum Beispiel hier links oben im Eck:
xInf=x(1); %Position in x-Richtung yInf=y(Ny); %Position in y-Richtung IndInf2=1; %Spalte IndInf1=Ny; %Zeile IndInf1neu=IndInf1; IndInf2neu=IndInf2; close all;
Bewegung der Individuen
[Bearbeiten]Nun soll eine zufällig Bewegung generiert werden. Dies wird durch den Befehl gewährleistet. Dieser Befehl erstellt eine X-Matrix (hier eine X-Matrix) mit Zufallszahlen zwischen und . Mit Hilfe des Subtrahenden (d.h. ) entstehen somit Zufallszahlen zwischen und . Anschließend wird die neue Position bzw. von jedem Punkt durch die Addition der Zufallszahl zwischen und zur jeder -Koordinate generiert und mit der gegebenen Geschwindigkeit (hier zunächst ) skaliert.
Nun sollen sich die einzelnen Individuen in eine zufällige, aber feste Richtung mit konstanter Geschwindigkeit bewegen:
g=0.50; %feste Geschwindigkeit, mit der sich die Fußgänger bewegen T=6; %Zeiteinheiten Zeitschritte=4; %pro eine Zeiteinheit T dt=1/Zeitschritte; %Zeitschritte % Zielpunkt neuPosX=x.+g.*rand(Ny,Nx)-0.5*g; %neue x-Koordinate neuPosY=y.+g*rand(Ny,Nx)-0.5*g; %neue y-Koordinate
Diese neuen Positionen werden jedoch nur schrittweise erreicht: In jedem Zeitschritt wird zur aktuellen Position ein entsprechender Bruchteil der Gesamtbewegung addiert.
Bewegung ohne einen Infizierten
[Bearbeiten]Infolgedessen ist das Generieren einer Zeitschleife notwendig (zunächst ohne einen Infizierten). Man erhält damit eine Reihe von Bildern, die sich als gif generieren lassen:

Anzahl=0; %Zur zeitlichen Darstellung der Infiziertenzahl %Zeitschleife für 4 Zeitschritte pro eine Zeiteinheit T: for i=1:T*Zeitschritte neuX=x.+1*(neuPosX.-x)*i*dt; %dt = 1/Zeitschritte neuY=y.+1*(neuPosY.-y)*i*dt; figure (i+1) title (['t=' num2str(i*dt)]) %Gibt die jeweilige Zeit (4 Zeitschritte pro eine Zeiteinheit T) als Titel an axis([-5 25 -5 15]); hold on; plot(neuX,neuY, '*b') ; hold off; endfor
Bewegung mit einem Infizierten
[Bearbeiten]Möchte man die Ausbreitung der Infektion über die Bewegung generieren, so muss man noch zusätzlich einen Infektionsradius angeben (hier zunächst ). Zusätzlich ist eine Anpassung der Zeitschleife notwendig, da nicht nur in der Endposition der Abstand zwischen den einzelnen Individuen überprüft werden muss, sondern in jedem Zeitschritt. Ist der Abstand zwischen zwei Punkten geringer als der Infektionsradius, so findet Infektion statt.

radiusInf=0.80 %Infektionsradius %Bewegung und Ausbreitung mit erstem Infizierten - mittig Anzahl=0; %Zur zeitlichen Darstellung der Infiziertenzahl %Zeitschleife für 4 Zeitschritte pro eine Zeiteinheit T: for i=1:T*Zeitschritte neuX=x.+1*(neuPosX.-x)*i*dt; neuY=y.+1*(neuPosY.-y)*i*dt; figure (i+1) title (['t=' num2str(i*dt)]) axis([-5 25 -5 15]); hold on plot(neuX,neuY, '*b') ; %neue Infizierungen: In den Vektoren IndInf1, IndInf2 sind die i- und j-Indexen der (x,y)-Koordinaten der bereits Infizierten gespeichert for k1=1:length(IndInf1) for j=1:Nx for l=1:Ny abstand=norm ( [neuX(l,j)-neuX(IndInf1(k1),IndInf2(k1)), neuY(l,j)-neuY(IndInf1(k1),IndInf2(k1))]); if abstand<radiusInf %Abstand < Infektionsradius? abstand; plot(neuX(l,j),neuY(l,j), 'sr') ; k2=1; while k2 <=length(IndInf1)&&(l!=IndInf1neu(k2) || j!=IndInf2neu(k2)) %Überprüfen: Schon in Vektor der Infizierten enthalten? k2=k2+1; endwhile if k2 >length(IndInf1) IndInf1neu=[IndInf1neu l]; IndInf2neu=[IndInf2neu j]; endif endif IndInf1=IndInf1neu; IndInf2=IndInf2neu; endfor endfor endfor hold off lengt=length(IndInf1) Anzahl= [Anzahl lengt]; endfor Infiz1=[IndInf1; IndInf2] %Ausabe Inizierten Indexen hold off;
Auswirkungen der Anfangsposition des Individuums
[Bearbeiten]Verändert man nun die Anfangsposition des infizierten Individuums, zum Beispiel an die Position oben links und verändert den Befehl dahingehend, eribt sich beispielweise folgende Situation. Dabei lässt sich bei mehreren Durchläufen beobachten, dass sich die Infektion von der Mitte aus deutlich stärker ausbreitet als beispielsweise vom Rand aus.


%Bewegung und Ausbreitung mit erstem infizierten - Position oben links Anzahl=0; % Zur zeitlichen Darstellung der Infiziertenzahl %Zeitschleife für 4 Zeitschritte pro eine Zeiteinheit T: for i=1:T*Zeitschritte neuX=x.+1*(neuPosX.-x)*i*dt; neuY=y.+1*(neuPosY.-y)*i*dt; figure (i+1) title (['t=' num2str(i*dt)]) axis([-5 25 -5 15]); hold on plot(neuX,neuY, '*b') ; %neue Infizierungen: In den Vektoren IndInf1, IndInf2 sind die i- und j-Indexen der (x,y)-Koordinaten der bereits Infizierten gespeichert. for k1=1:length(IndInf1) for j=1:Nx for l=1:Ny abstand=norm ( [neuX(l,j)-neuX(IndInf1(k1),IndInf2(k1)), neuY(l,j)-neuY(IndInf1(k1),IndInf2(k1))]); if abstand<radiusInf %Abstand < Infektionsradius? abstand; plot(neuX(l,j),neuY(l,j), 'sr') ; k2=1; while k2 <=length(IndInf1)&&(l!=IndInf1neu(k2) || j!=IndInf2neu(k2)) %Überprüfen: Schon in Vektor der Infizierten enthalten? k2=k2+1; endwhile if k2 >length(IndInf1) IndInf1neu=[IndInf1neu l]; IndInf2neu=[IndInf2neu j]; endif endif IndInf1=IndInf1neu; IndInf2=IndInf2neu; endfor endfor endfor hold off lengt=length(IndInf1) Anzahl= [Anzahl lengt]; endfor Infiz1=[IndInf1; IndInf2] %Ausabe Inizierten Indexen hold off;
Die Grafik unterhalb der Simulation verdeutlicht, dass die zentrale Position des infizierten Individuum sich deutlich schneller ausbreitet als eine Positionierung am Rande. Infolgedessen lässt sich darauf schließen, dass sich eine Infektion, die ihren Ursprung am Rand hat, dementsprechend langsamer ausbreitet. Dies könnten wir als Containment (engl. containment für "Eindämmung" oder "Zusammenhalten") interpretieren: Durch die räumliche Isolation in Teilen wird die Ausbreitung der Infektion gebremst. Allerdings ist es beinahe unmöglich, den Ursprung der Infektion frühzeitig einzudämmen, weil wir uns gerade erst am Anfang der Virusausbreitung befinden.
Auswirkungen verschiedener Infektionsradien
[Bearbeiten]Nachfolgend betrachten wir nun, inwieweit sich eine Veränderung des Infektionsradius auf das Infektionsgeschehen auswirkt. Dabei ist zu erwarten, dass eine Vergrößerung des Infektionsradius ein erhöhtes Infektionsgeschehen mit sich führt. Umgekehrt sollte demnach eine Verkleinerung des Radius zu einem weniger ausgeprägten Infektionsgeschehen führen. Zunächst möchten wir den Infektionsradius vergrößern.
Vergrößerung des Infektionsradius
[Bearbeiten]Zur Vergrößerung des Radius addieren wir , also genau die Hälfte unseres ursprünglichen Infektionsradius.

%Bewegung mit Infizierten radiusInf=1.2; %neuer Infektionsradius (vorher radiusInf=0.8;) %erstes infizierte Individuum - mittig xInf=x(1,Nx/2); yInf=y(Ny/2); IndInf2=Nx/2; IndInf1=Ny/2; IndInf1neu=IndInf1; IndInf2neu=IndInf2; %Bewegung und Ausbreitung mit erstem infizierten - mittig Anzahl=0; %Zur zeitlichen Darstellung der Infiziertenzahl %Zeitschleife für 4 Zeitschritte pro eine Zeiteinheit T: for i=1:T*Zeitschritte neuX=x.+1*(neuPosX.-x)*i*dt; neuY=y.+1*(neuPosY.-y)*i*dt; figure (i+1) title (['t=' num2str(i*dt)]) axis([-5 25 -5 15]); hold on plot(neuX,neuY, '*b') ; %neue Infizierungen: In den Vektoren IndInf1, IndInf2 sind die i- und j-Indexen der (x,y)-Koordinaten der bereits Infizierten gespeichert for k1=1:length(IndInf1) for j=1:Nx for l=1:Ny abstand=norm ( [neuX(l,j)-neuX(IndInf1(k1),IndInf2(k1)), neuY(l,j)-neuY(IndInf1(k1),IndInf2(k1))]); if abstand<radiusInf %Abstand < Infektionsradius? abstand; plot(neuX(l,j),neuY(l,j), 'sr') ; k2=1; while k2 <=length(IndInf1)&&(l!=IndInf1neu(k2) || j!=IndInf2neu(k2)) %Überprüfen: Schon in Vektor der Infizierten enthalten? k2=k2+1; endwhile if k2 >length(IndInf1) IndInf1neu=[IndInf1neu l]; IndInf2neu=[IndInf2neu j]; endif endif IndInf1=IndInf1neu; IndInf2=IndInf2neu; endfor endfor endfor hold off lengt=length(IndInf1) Anzahl= [Anzahl lengt]; endfor Infiz1=[IndInf1; IndInf2] %Ausabe Inizierten Indexen hold off;
Man erkennt, dass bereits eine Vergrößerung des Infektionsradius um einen erheblichen Effekt auf das Infektionsgeschehen ausübt: Die Infektionen breitet in einem rasanten Tempo aus.
Verkleinerung des Infektionsradius
[Bearbeiten]Zur Verkleinerung des Radius subtrahieren , also wieder genau die Hälfte des ursprünglichen Infektionsradius.

%Bewegung mit Infiziertem radiusInf=0.4; %neuer Infektionsradius (vorher radiusInf=0.8;) %erstes infizierte Individuum - mittig xInf=x(1, Nx/2); yInf=y(Ny/2); IndInf2=Nx/2; IndInf1=Ny/2; IndInf1neu=IndInf1; IndInf2neu=IndInf2; %Bewegung und Ausbreitung mit erstem infizierten - mittig Anzahl=0; % Zur zeitlichen Darstellung der Infiziertenzahl %Zeitschleife für 4 Zeitschritte pro eine Zeiteinheit T: for i=1:T*Zeitschritte neuX=x.+1*(neuPosX.-x)*i*dt; neuY=y.+1*(neuPosY.-y)*i*dt; figure (i+1) title (['t=' num2str(i*dt)]) axis([-5 25 -5 15]); hold on plot(neuX,neuY, '*b') ; %neue Infizierungen: In den Vektoren IndInf1, IndInf2 sind die i- und j-Indexen der (x,y)-Koordinaten der bereits Infizierten gespeichert for k1=1:length(IndInf1) for j=1:Nx for l=1:Ny abstand=norm ( [neuX(l,j)-neuX(IndInf1(k1),IndInf2(k1)), neuY(l,j)-neuY(IndInf1(k1),IndInf2(k1))]); if abstand<radiusInf %Abstand < Infektionsradius? abstand; plot(neuX(l,j),neuY(l,j), 'sr') ; k2=1; while k2 <=length(IndInf1)&&(l!=IndInf1neu(k2) || j!=IndInf2neu(k2)) %Überprüfen: Schon in Vektor der Infizierten enthalten? k2=k2+1; endwhile if k2 >length(IndInf1) IndInf1neu=[IndInf1neu l]; IndInf2neu=[IndInf2neu j]; endif endif IndInf1=IndInf1neu; IndInf2=IndInf2neu; endfor endfor endfor hold off lengt=length(IndInf1) Anzahl= [Anzahl lengt]; endfor Infiz1=[IndInf1; IndInf2] %Ausabe Inizierten Indexen hold off;
Vergleich der verschiedenen Infektionsradien
[Bearbeiten]Beim Vergleich der beiden Infektionsradien ist ein signifikanter Unterschied erkennbar: Während ein Infektionsradius von kaum Infektionen mit sich bringt, schießen die Infektionen innerhalb eines Infektionsradius von geradezu in die Höhe. Erst ab einer Zeit von wachsen die Infektionszahlen nicht mehr so rasant, bleiben aber weiterhin auf einem beständig hohen Niveau. Dieses Abklingen der Änderungsrate der Infektionen lässt sich damit begründen, dass sich die Infektionen zwischen der Startzeit und so schnell stattfanden, dass nachfolgend nicht mehr viele nicht-infizierte Individuen übrig sind, die sich noch anstecken können. Diesen Zusammenhang werden wir im SIR-Modell noch genauer untersuchen. Weiterhin fällt auf, dass kein linearer Zusammenhang zwischen dem Infektionsradius und der Anzahl der Infektionen vorliegen kann: Ein dreimal so großer Infektionsradius ( im Vergleich zu ) bringt deutlich mehr als dreimal so viele Infektionen mit sich. Dahinter vermuten wir einen exponentiellen Zusammenhang. Auch diesen werden wir im SIR-Modell genauer betrachten.

Aus der Grafik lässt sich deutlich entnehmen, dass ein größerer Infektionsradius ein vermehrtes Infektionsgeschehen begünstigt. Ein größerer Infektionsradius lässt sich sinnbildhaft als Missachtung von Hygieneregeln interpretieren: Passanten husten ohne die Hand vor den Mund zu halten oder niesen nicht in ihre Ellenbeugen. Die Vergrößerung des Infektionsradius kann auch symbolisch sein für das Begrüßen der Passanten untereinander mit Händedruck. Umgekehrt hemmt ein geringerer Infektionsradius die Infektionsausbreitung, was beispielsweise als Verwenden von Mund-Nasen-Bedeckungen interpretiert werden kann. Hierbei kann man weitere Abstufungen vornehmen, indem man von unterschiedlichen Maskenarten (Stoffmaske, OP-Maske, FFP1, FFP2, etc.) ausgeht.
Diskussion: Infektionsradius größer als der Abstand
[Bearbeiten]Doch was passiert, wenn der Radius größer als der ursprüngliche Abstand der Punkte ist (hier größer als )? Aus obiger Simulation () lässt sich entnehmen, dass die Infektionen sehr schnell stattfinden. Doch inwiefern trägt in diesem Fall die Bewegung der Punkte etwas dazu bei? Würde die Infektion sich in diesem Fall verbreiten auch ohne Bewegung? Dies lässt sich aus der folgenden Grafik herauslesen:

Der rote Graf entspricht der bewegten Ausbreitung bei einem Infektionsradius größer als (hier ). Wie erwartet finden die Infektionen statt.
Dem gegenüber entspricht der blaue Graf der unbewegten Ausbreitung bei einem gleichen Infektionsradius größer als (hier ). Es lässt sich beobachten, dass sich die Infektion im unbewegten Zustand schneller ausbreitet als im bewegten Zustand und zu einem bestimmten Zeitpunkt alle infiziert sind.Dies lässt sich damit erklären, dass die Bewegung nicht nur die Infektion antreiben, sondern auch dämpfen kann, da sich durch die Bewegung der Abstand zu den infizierten Punkten nicht zwingend verkleinern, sondern (bedingt durch die konstante Richtung) auch vergrößern kann.
Dementsprechend begünstigt in den Fällen mit einem kleinerem Radius als der ursprüngliche Abstand die Bewegung die Ausbreitung des Infektionsgeschehen, während in den Fällen mit einem größeren Radius die Ausbreitung des Infektionsgeschehens minimal gehemmt wird.
Auswirkungen verschiedener Simulationszeiten
[Bearbeiten]Nun betrachten wir, wie sich eine Veränderung der Simulationszeit auf das Infektionsgeschehen ausübt. Zunächst betrachten wir die Auswirkungen, die eine Vergrößerung der Simulationszeit.
Vergrößerung der Simulationszeit
[Bearbeiten]Hierzu nehmen wir eine Verdopplung der Zeiteinheiten vor, d.h. . Der Einfachheit halber betrachten wir hier nun statt bloß Zeitschritte pro Zeiteinheit. Wir erwarten, dass die Ausbreitung der Infektionen begünstigt wird.

Nx=20; %Anzahl der Punkte in x Richtung Ny=10; %Anzahl der Punkte in y Richtung Zeitschritte=2; %pro eine Zeiteinheit T=1 (vorher Zeitschritte=4) T=12; %Die Berechnung wird für 12 Zeiteinheiten laufen (vorher T=6) g=0.50; %Geschwindigkeit mit der sich die Fußgänger bewegen x=[1:Nx]; y=[1:Ny]; dt=1/Zeitschritte; %Weiter wie vorher
Tatsächlich lässt sich eine erhöhtes Infektionsgeschehen beobachten.
Reduzierung der Simulationszeit
[Bearbeiten]Betrachten wir nun die Auswirkungen einer Reduzierung der Simulationszeit an. Hierzu halbieren wir unsere ursprüngliche Zeiteinheit, d.h. . Die Anzahl der Zeitschritte () pro Zeiteinheit bleibt unverändert gegenüber der ursprünglichen Einstellung.

Nx=20; %Anzahl der Punkte in x Richtung Ny=10; %Anzahl der Punkte in y Richtung Zeitschritte=4; %pro eine Zeiteinheit T=1 T=3; %Die Berechnung wird für 3 Zeiteinheiten laufen (vorher T=6) g=0.50; %Geschwindigkeit mit der sich die Fußgänger bewegen x=[1:Nx]; y=[1:Ny]; dt=1/Zeitschritte; %Weiter wie vorher
Wie zu erwarten, bleibt das Infektionsgeschehen überschaubar.
Auswirkungen verschiedener Bewegungsgeschwindigkeiten
[Bearbeiten]

Ein weiterer interessanter Aspekt ist der Einfluss der Bewegungsgeschwindigkeit auf das Infektionsgeschehen. Abermals ist dabei zu erwarten, dass eine Erhöhung der Bewegungsgeschwindigkeit ein erhöhtes Infektionsgeschehen mit sich führt. Umgekehrt wird dementsprechend erwartet, dass eine Reduzierung der Bewegungsgeschwindigkeit zu einem weniger ausgeprägten Infektionsgeschehen führt.
Zur Demonstration der Erhöhung der Bewegungsgeschwindigkeit der Individuen wird diese zunächst einmal verfünffacht (d.h. ):
g=2.5; %Geschwindigkeit mit der sich die Fußgänger bewegen (vorher g=0.5) neuPosX=x.+g.*rand(Ny,Nx)-0.5*g; neuPosY=y.+g*rand(Ny,Nx)-0.5*g; %Rest wie gehabt
Zur Demonstration der Reduzierung der Bewegungsgeschwindigkeit der Individuen wird die Ursprungsgeschwindigkeit mit 5 dividiert (d.h. ):
g=0.1; %Geschwindigkeit mit der sich die Fußgänger bewegen (vorher g=0.5) neuPosX=x.+g.*rand(Ny,Nx)-0.5*g; neuPosY=y.+g*rand(Ny,Nx)-0.5*g; %Rest wie gehabt
Ein direkter Vergleich ergibt folgende Grafik:

Es ist deutlich erkennbar, dass sich die höhere Bewegungsgeschwindigkeit stark auf das Infektionsgeschehen auswirkt. Im gleichen Zeitraum bleibt bei einer Geschwindigkeit von die Anzahl der Infektionen unter und bei einer Geschwindigkeit von unter . Bei einer Geschwindigkeit von finden beinahe Infektionen statt.
Geschwindigkeitspfeile
[Bearbeiten]Um die einzelnen Schritte besser nachvollziehen zu können, generieren wir für jeden Punkt den zugehörigen Geschwindigkeitspfeil mit folgendem Befehl: :

for i=1:T*Zeitschritte neuX=x.+1*(neuPosX.-x)*i*dt; % dt = 1/Zeitschritte neuY=y.+1*(neuPosY.-y)*i*dt; figure (i+1) title (['t=' num2str(i*dt)]) axis([-5 25 -5 15]); hold on; quiver(neuX,neuY,neuPosX.-x, neuPosY.-y) plot(neuX,neuY, '*b') ; hold off; endfor
Bewegungsrichtungen
[Bearbeiten]Nachfolgend soll die Bewegungsrichtung der einzelnen Punkten nicht mehr konstant sein, sondern sich nach jedem Schritt zufällig ändern. Dabei bleibt jedoch die Grundstruktur des Modells erhalten.

%Grundgerüst
Nx=20; %Anzahl der Punkte in x Richtung
Ny=10; %Anzahl der Punkte in y Richtung
g=0.50; %feste Geschwindigkeit, mit der sich die Fußgänger bewegen
T=6; %Zeiteinheiten
Zeitschritte=4; %pro eine Zeiteinheit T=1
radiusInf=0.80;%Infektionsradius
%--------------------------------------------------------------------------------------------
dt=1/Zeitschritte;
x=[1:Nx];
y=[1:Ny];
[x,y]=meshgrid (x,y) %erzeugt das Punktgitter
%Ausgabe "Keine Infektion" als Grafik:
figure (1)
hold on;
plot(x,y, '*b') ;
axis([-5 25 -5 15]);
hold off;
%Erster Infizierter (mittig)
xInf1=x(1, Nx/2); %Position in x-Richtung
yInf1=y(Ny/2); %Position in y-Richtung
IndInf2=Nx/2; %Spalte
IndInf1=Ny/2; %Zeile
IndInf1neu=IndInf1;
IndInf2neu=IndInf2;
close all;
%Ausgabe "Ein Infizierter in der Mitte" als Grafik:
figure (2)
hold on;
plot(x,y, '*b') ;
plot(xInf1,yInf1, 'sr') ;
axis([-5 25 -5 15]);
hold off;
%neue Position
% Zielpunkt
neuPosX=x.+g.*rand(Ny,Nx)-0.5*g;
neuPosY=y.+g*rand(Ny,Nx)-0.5*g;
neuPosX2=neuPosX.+g.*rand(Ny,Nx)-0.5*g;
neuPosY2=neuPosY.+g*rand(Ny,Nx)-0.5*g;
%Bewegung mit Infizierter Person:
Anzahl=0; %Zur zeitlichen Darstellung der Infiziertenzahl
%Zeitschleife für 4 Zeitschritte pro eine Zeiteinheit T:
for i=1:T*Zeitschritte
neuX=x.+1*(neuPosX.-x)*1*dt;
neuY=y.+1*(neuPosY.-y)*1*dt;
x=neuX;
y=neuY;
neuPosX=neuX.+g.*rand(Ny,Nx)-0.5*g;
neuPosY=neuY.+g.*rand(Ny,Nx)-0.5*g;
figure (i+2)
title(['t=' num2str(i*dt)])
plot(neuX,neuY, '*b') ;
hold on;
axis([-5 25 -5 15]);
quiver(neuX,neuY,neuPosX.-x,neuPosY.-y,'m')
title(['t=' num2str(i*dt)])
for k1=1:length(IndInf1)
for j=1:Nx
for l=1:Ny
abstand=norm ( [neuX(l,j)-neuX(IndInf1(k1),IndInf2(k1)), neuY(l,j)-neuY(IndInf1(k1),IndInf2(k1))]);
if abstand<radiusInf
abstand;
plot(neuX(l,j),neuY(l,j), 'sr') ;
%---------------------------
k2=1;
while k2 <=length(IndInf1)&&(l!=IndInf1neu(k2) || j!=IndInf2neu(k2))
k2=k2+1;
endwhile
if k2 >length(IndInf1)
IndInf1neu=[IndInf1neu l];
IndInf2neu=[IndInf2neu j];
endif
endif
endfor
endfor
endfor
IndInf1=IndInf1neu;
IndInf2=IndInf2neu;
hold off
lengt=length(IndInf1);
endfor
Tutoriumsaufgabe 2: Fundamentallösungen
[Bearbeiten]Theoretische Grundlagen
[Bearbeiten]Eine weitere Möglichkeit der Modellierung der Ausbreitung einer Infektion stellt die kontinuerliche Diffusionsmodellierung dar. Diese basiert auf die räumliche Diffusion. Darunter versteht man die zufällige Bewegung der Molekule eines Stoffes (vgl. hierzu die Brownsche Bewegung). Zunächst soll nachfolgend einfachheitshalber nur der homogene Diffusionsprozess betrachtet werden.
Mathematisch wird dieser Diffusionsprozess durch die folgende partielle Differentiagleichung beschrieben: wobei die Funktion :
- die unbekannte Teilchenkonzentrationsdichte/Temperaturdichte und
- den ortsabhängigen Diffusion-/Wärmeleitkoeffizienten beschreibt.
Die Herleitung beruht dabei ausschließlich auf die zwei folgenden physikalischen Gesetzen:
- Ficksches Gesetz:
- Die Diffusionsflussrate (Teilchenstromdichte) ist proportional zum Konzentrationsgradient, mit dem negativen ortsabhängigen Diffusionskoeffizienten (Proportionalitätskonstante) und es gilt:
- Die Teilchen bewegen sich in der Richtung des Konzentrationsabfalls.
- Massenerhaltungssatz.
- Erhaltungssatz: Der Stoff in einem Volumen entsteht oder verschwindet nicht, sondern bleibt erhalten (sofern nicht von aussen zugefügt oder weggenommen).
Stationäre (zeitunabhängige) Diffusion im eindimensionalen Raum
[Bearbeiten]Nach dem Fick’schen Gesetz ist die Teilchenstromdichte proportional zum Konzentrationsgradienten mit der Proportionalitätskonstante, dem negativen ortsabhängigen Diffusionskoeffizienten . Dabei gibt an, wieviel Teilchen in einem Ort von links nach rechts diffundieren. Somit erhält man folgende Gleichung für die Teilchenstromdichte: Folglich bewegen sich die Teilchen in der Richtung des Konzentrationsabfalls.
Ferner kann innerhalb eines Systems nach dem Massenerhaltungsgesetz keine Masse von selbst entstehen oder verschwindet, sondern bleibt erhalten (sofern diese nicht von außen zugefügt oder weggenommen wurde). Dementsprechend sollte sich die Gesamtanzahl der Teilchen in einem dem Intervall zwischen und , gegeben durch nicht ändern.
Durch die Brownsche Molekularbewegung kommt es zum Austausch der Teilchen an den Rändern , sodass der Zufluss am linken Rand () mit dem Ausfluss am rechten Rand () ausgeglichen werden muss. Daraus folgt:
Durch die Division durch (mit ) ergibt sich der Differenzenquotient : .
Für den Grenzübergang folgt daraus die sogenannte Erhaltungsgleichung
Setzen wir nun aus in ein, ergibt sich daraus:
Ist ferner der Diffusionskoeffizient konstant, so ergibt sich dann Dies entspricht der Laplace Gleichung im eindimensionalen Raum.
Zeitabhängige Diffusion im eindimensionalen Raum
[Bearbeiten]Die Herleitung der Gleichung für die zeitabhängige Diffusion erfolgt nahezu analog zur stabilen Diffusionsgleichung im eindimensionalen Raum. Der Hauptunterschied liegt in der gesuchten Dichtefunktion , die nun zusätzlich auch von der Zeit abhängt:
Da sich die Aussage des Fick'schen Gesetzes nicht ändert, erhält man die nachfolgende Gleichung für die Teilchenstromdichte: (Nach wie vor gibt an, wieviel Teilchen in einem Ort von links nach rechts diffundieren und den negativen ortsabhängigen Diffusionskoeffizienten .)
Beim Massenerhaltungssatz muss jedoch noch die zeitliche Veränderung angepasst werden, das heißt, dass der Einfluss am linken Rand nicht mehr dem Ausfluss am rechten Rand entspricht. Stattdessen deckt die Differenz der beiden Werte der zeitlichen Veränderung der Gesamtanzahl der Teilchen.
Abermals wird durch die Division durch und der Betrachtung beim Grenzübergang der Differenzquotient gebildet und man erhält:
Setzen wir nun aus in ein, ergibt sich daraus die homogene Diffusionsgleichung: bzw.
Inhomogene Diffusionsgleichung
[Bearbeiten]Für die Herleitung der inhomogene Diffusionsgleichung beeinflusst zusätzlich ein Quellterm das Massenerhaltungsgesetz. Das bedeutet, dass in das System von Außen zusätzlich Teilchen hinzugefügt werden bzw. innerhalb des Systems neue Teilchen entstehen (zum Beispiel bei einer chemischen Reaktion oder beim Populationswachstum):
Dementsprechend erhält man nach dem Grenzübergang die inhomogene Diffusionsgleichung:
Analytische Lösung: Stationäre (zeitunabhängige) Diffusion
[Bearbeiten]Implementierung der Fundamentallösung der Laplace Gleichung
[Bearbeiten]Die Formel der Fundamentallösung der Laplace-Gleichung für lautet:
Dabei beschreibt das Volumen der Einheitskugel in und die Vektornorm in . Indessen ist unabhängig von der Zeit und nur von einer räumlichen Variablen abhängig, es gilt also . Ferner sei zusätzlich zu beachten, dass die Fundamentallösung keine eigentliche Lösung der Laplace-Gleichung ist, wenn der Ursprung in liegt, da sie in diesem Punkt eine Singularität aufweist.
Zunächst erstellen wir ein Gitter, wobei der Abstand derart passend gewählt wird, sodass der Punkt aus dem Gitter 'ausgeschnitten' wird (Grund: Singularität).
step=0.1; X=[-1:step:-0.01, 0.01:step:1]; Y=[-1:step:-0.01, 0.01:step:1]; [x,y]=meshgrid(X,Y);
Im zweidimensionalen Raum lautet die Formel der Fundamentallösung .
phi=@(x,y) -1/(2*pi)*log(sqrt(x.^2+y.^2));
Die Lösung wollen wir nun plotten.
figure 1
meshc(x ,y, phi(x,y))
grid on
axis([-3 3 -3 3 -1 1])
xlabel('x')
ylabel('y')
zlabel('z')
title('Fundamentalloesung der Laplace-Gleichung')
Implementierung der Fundamentallösung der Poisson Gleichung
[Bearbeiten]Die Lösung der inhomogenen Laplace-Gleichung , der Poisson-Gleichung auf wird mithilfe der Faltung der Fundamentallösung und der Funktion der rechten Seite berechnet (Poissonformel) [10]: (Kurz: Bei der Darstellung der Poisson-Gleichung wird im Vergleich zur Fundamentallösung der Laplace-Gleichung zusätzlich ein Quellterm auf der rechten Seite der Gleichung betrachtet.)
Die Funktion stellt dabei eine Funktion mit kompakten Träger dar und es gilt: .

Dabei wird zuerst die Quellfunktion implementiert.
function wert=Quellfunktion(x,y) if sqrt((x.-0.6).^2+(y.-0.8).^2)<=0.3 wert=1; else wert=0; endif endfunction
Anhand der Abbildung erkennt man, dass die Quellfunktion eine Funktion mit kompakten Träger darstellt: Innerhalb eines bestimmten Gebietes entspricht der Wert der Quellfunktion 1 und ansonsten 0.
Zunächst wird ein rechteckiges Gitter erstellt:
step=0.03; X=[0:step:2]; Y=[0:step:2]; [x,y]=meshgrid(X,Y);
Anschließend erfolgt die Definition der Funktionswerte sowie das Einfügen der Quellfunktion:
for i=1:(length(X)) for j=1:(length(Y)) f(j,i)=1*Quellfunktion(x(j,i),y(j,i)); endfor endfor
Erst in einem nächsten Schritt erfolgt die Implementierung der Poissonformel:
for i=1:(length(X)) for j=1:(length(Y)) xstar=x(j,i)*ones(length(Y),length(X)); ystar=y(j,i)*ones(length(Y),length(X)); % Phi mit verschobenem Argument: phi=-log(sqrt((xstar.-x).^2+(ystar.-y).^2))/(2*pi); phi(j,i)=0; %numerische Integration I(j,i) = trapz(Y,trapz(X,phi.*f,1),2); endfor endfor
Die Werte der Fundamentalfunktion werden dabei um ein festes für jeden Gitterpunkt verschoben und in einer Matrix φ gespeichert. wird dabei durch die for-Schleife als Matrix mit konstanten Einträgen beschrieben, damit die Differenz der Argumente als Differenz der Matrizen durchführbar ist. Ferner wird für φ aufgrund der Singularität für festgeschrieben. Der Wert des Integrals wird dabei nicht verändert, da es eine Menge vom Maß Null ist. Anschließend wird das doppelte Integral mit der Trapezregel gelöst.
Abschließend folgt nur noch die grafische Ausgabe der Poisson-Gleichung:

%Grafische Ausgabe der Funktion auf der rechten Seite [vgl. Abbildung oben]
figure 1
surfc(x,y,f)
title ('Funktion der rechten Seite')

%Grafische Ausgabe 2:
figure 2
surfc(x,y,I)
title ('Loesung der Poisson-Gleichung')
figure 3
meshc(x,y,I)
grid on
title ('Losung von Poissongleichung')
xlabel('x')
xlabel ('y')
view([0,2,-1])
Instationäre (zeitabhängige) Diffusion (Tutoriumsaufgabe)
[Bearbeiten]Nun wollen wir den instationären Fall betrachten. Dieser unterscheidet sich vom stationären durch die Abhängigkeit von der Zeitvariablen .
Homogene instationäre Diffusion
[Bearbeiten]Für die homogene instationäre Diffusionsgleichung ist uns die folgende Lösungsformel bereits bekannt:
Dabei ist das Quadrat der euklidischen Norm von .
Unser Gitter bleibt zunächst unverändert.
step=0.1; % Schrittweite X=[-1:step:-0.01, 0.01:step:1]; % X ohne Null Y=[-1:step:-0.01, 0.01:step:1]; % Y ohne Null [x,y]=meshgrid(X,Y); % Gitter
Anschließend definiert man den Diffusionskoeffizienten und erstellt eine Zeitschleife, um die Abhängigkeit von t festzulegen:
a=0.2; %Konstanter Diffusionskoeffizient T=3; %Anzahl der Zeiteinheiten Zeitschritte=3; %Anzahl der Zeitschritte dt=1/(Zeitschritte*T); %Zwischenschritte t_0=0.1; %Anfangsbedingung
Erst in einem nächsten Schritt wird die bekannte Fundamentallösung der homogenen instationären Diffusionsgleichung angegeben und grafisch ausgegeben:

for i=0:T*Zeitschritte;
t=t_0+i*dt
psi=@(x,y,t) 1/(4*pi*a*t)*exp(-sqrt(x.^2+y.^2)/(4*a*t));
%grafische Ausgabe
figure (i+1)
meshc(x,y,psi(x,y,t))
grid on
title(['Zeitabhaengige Diffusion nach t=',num2str(t_0+i*dt)])
xlabel('x')
ylabel('y')
zlabel('z')
axis([-2 2 -2 2 0 1.1])
endfor
Anfangswertproblem der instationären, homogenen Diffusionsgleichung
[Bearbeiten]Im zweiten Teil der Tutoriumsaufgabe 2 soll nun die vorherige Diffusionsgleichung mit einer Anfangsbedingung um ein Anfangswertproblem ergänzt werden:
Die homogene, instationäre Diffusionsgleichung , mit konstanten Diffusionskoeffizient werden nun um eine Anfangsbedingung : ergänzt, die im Anfangszeitpunkt die Konzentrationsdichte bzw die Dichte der Infizierten beschreibt. Dementsprechend ist die Lösung des (homogenen) Anfangswertproblem für ist durch die Faltung der Fundamentallösung mit der Anfangsfunktion gegeben :
Und ähnlich wie bei der Poisson-Gleichung ist diese Faltung auch dann beschränkt, wenn diese Anfangswertfunktion beschränkt ist und einen kompakten Träger hat. Da zusätzclih in eine Singularität hat, ist auch dieses Anfangswertproblem in singulär.
Bei der Programmierung wurde die Quellfunktion derart angepasst werden, dass nun mehrere Infektionsherden (hier vier) gegeben sind:
function wert=Quellfunktion_2(x,y)
if sqrt((x.-0.3).^2+(y.-0.3).^2)<=0.1 wert=1;
else wert=0;
if sqrt((x.-0.3).^2+(y.-1.3).^2)<=0.2 wert=0.8;
else wert=0;
if sqrt((x.-1.5).^2+(y.-0.3).^2)<=0.07 wert=0.5;
else wert=0;
if sqrt((x.-1.5).^2+(y.-1.3).^2)<=0.3 wert=0.2;
else wert=0
endif
endif
endif
endif
endfunction
Wie bisher folgt nun die Erstellung des Gitters:
step=0.03; X=[0:step:2]; Y=[0:step:2]; [x,y]=meshgrid(X,Y);
Anschließend definiert man den Diffusionskoeffizienten und erstellt eine Zeitschleife, um die Abhängigkeit von t festzulegen:
a=0.2; %Konstanter Diffusionskoeffizient T=3; %Anzahl der Zeiteinheiten Zeitschritte=3; %Anzahl der Zeitschritte dt=1/(Zeitschritte*T); %Zwischenschritte t_0=0.1; %Startzeit
Darauf folgt die Festlegung der Funktionswerte in allen Punkten und die Initialisierung der Quellfunktion mit ihren vier Infektionsherden, die auf dem Gitter als unbeschränktes Gebiet verteilt werden:
for i=1:(length(X)) for j=1:(length(Y)) u0(j,i)=1*Quellfunktion_2(x(j,i),y(j,i)); endfor endfor
Erst dann erfolgt die Implementierung der Faltung. Die eingefügte Zeitschleife sichert dabei die zeitliche Abhängigkeit. Schlussendlich muss die Diffusion nur noch grafisch ausgegeben werden:

for s=0:T*Zeitschritte
t=t_0+s*dt
for i=1:(length(X))
for j=1:(length(Y))
xstar=x(j,i)*ones(length(Y),length(X)); %Verschiebung um ein festes x*
ystar=y(j,i)*ones(length(Y),length(X)); %Verschiebung um ein festes y*
% Psi mit verschobenem Argument:
psi=(1/(4*pi*a*t))*exp(-(((xstar.-x).^2+(ystar.-y).^2))/(4*a*t)); %Speicherung der verschobenen Werte in Psi
%numerische Integration
I(j,i,s+1) = trapz(Y,trapz(X,psi.*u0,2));
endfor
endfor
%grafische Ausgabe
figure (s+1)
meshc(x,y,I(:,:,s+1))
grid on
title(['Loesung der instationaeren, inhomogenen Diffusion=', num2str(t_0+s*dt)])
xlabel('x')
ylabel('y')
zlabel('z')
axis([0 2 0 2 0 0.35])
endfor
Tutoriumsaufgabe 3: SIR-Modell
[Bearbeiten]Theoretische Grundlagen
[Bearbeiten]Exponentielles Wachstum
[Bearbeiten]bezeichnet die kumulierte Anzahl der infizierten Individuen zum Zeitpunkt . bezeichnet den Anfangswert der infizierten Individuen. Die Anzahl der Infizierten im neuen Zeitpunkt errechnet sich durch die Formel
mit der Infektionsrate . Diese Infektionsrate lässt sich als Wahrscheinlichkeit einer Infektion zwischen zwei Individuen auffassen. Das exponentielle Modell nutzt also die Zahl der Infizierten im alten Zeitpunkt sowie die Änderung über den Zeitabschnitt, um die Zahl der Infizierten im neuen Zeitpunkt zu bestimmen. Durch das Teilen der Gleichung
durch sowie dem Grenzübergang erhalten wir das exponentielle Wachstumsmodell
mit der Exponentialfunktion als Lösung:
Da dieses Modell - wie der Name bereits impliziert - die rasant ansteigende, exponentielle Ausbreitung des Infektionsgeschehens erkennbar macht, ist es besonders für die akkurate Beschreibung von Anfangszuständen einer Pandemie geeignet. Es lässt dabei allerdings außer Acht, dass früher oder später eine Sättigung der Population statt findet. Da die Zahl der Infizierten nicht ins Unendliche steigen kann, sondern durch die Gesamtpopulation begrenzt ist, ist das exponentielle Wachstumsmodell weniger geeignet, langfristige epidemiologische Prozesse zu beschreiben.
Logistisches Wachstumsmodell
[Bearbeiten]Die Sättigung der Population soll nun mit einbezogen werden. Hierzu wird das logistische Wachstumsmodell betrachtet. Dieses sagt aus, dass das Populationswachstum stärker verlangsamt, je weniger freie Kapazität sich im System befindet. Im immunologischen Kontext beschreibt die freie Kapazität die Zahl der potentiellen Infektionsträger, also Individuen, die sich (noch) nicht mit dem Virus infizierten. Ausgehend von einer konstanten Gesamtpopulation wird die freie Kapazität durch beschrieben.
Die Änderung der Zahl der Infizierten im neuen Zeitpunkt ist also proportional dem Bestand der Infizierten und der freien Kapazität . Die Proportionalitätskonstante heißt logistische Wachstumsrate. Durch den Grenzübergang erhalten wir das logistische bzw. beschränkte Wachstumsmodell
mit logistischer Funktion als Lösung:
Die beiden genannten Modelle, das exponentielle als auch logistische, sind rein dynamische, also zeitabhängige Modelle, d.h. sie betrachten keinen räumlichen Austausch der Diffusion.
SI-Modell
[Bearbeiten]Als einfachstes der sogenannten Kompartimentmodellen teilt das SI-Modell die Gesamtpopulation in zwei Gruppen ein: kumulierte Infizierte (engl. 'infected', ) und Empfängliche (engl. 'susceptible', ). Es nimmt an, dass genesene Individuen aus der Gruppe der Infizierten gegen künftige Infektionen immun sind und nicht erneut in die Gruppe der Empfänglichen wechseln. Das SI-Modell, auch logistisches Modell genannt, lässt sich also wie folgt durch Differentialgleichungen ausdrücken:
Aus den beiden Differentialgleichungen folgt die Erhaltungsgleichung , die besagt, dass die Gesamtpopulation konstant bleibt. Das SI-Modell lässt Neugeborene außer Acht und ordnet Verstorbene den kumulierten Infizierten zu.
SIR-Modell
[Bearbeiten]Aufbauend auf dem SI-Modell betrachtet das SIR-Modell eine dritte Gruppe, die der aus dem System entnommenen (engl. 'removed', ). Diese Gruppe beinhaltet Individuen, die, nachdem sie die sich infiziert haben, entweder gestorben sind (engl. 'deceased') oder genesen sind (engl. 'recovered'). Der Wechsel zwischen den beiden Gruppen der Infizierten und Removed erfolgt mit einer bestimmten Wechselrate (Umkehrwert der Genesungszeit bzw. infektiösen Periode ). Die Wechselrate des Auslösers der COVID-19 Erkrankung, SARS-CoV-2, hat beispielsweise eine Wechselrate von
Das SIR-Modell lässt sich durch drei Differentialgleichungen beschreiben:
Es gilt die Erhaltungsgleichung die besagt, dass die Gesamtpopulation konstant erhalten bleibt.
Modifiziertes SIR-Modell
[Bearbeiten]Für den Fall, dass die gestorbenen Infizierten nicht in der Gruppe der Genesenen erfasst werden sollen, kann das SIR-Modell wie folgt modifiziert werden:
mit den Anfangsbedingungen und den folgenden Variablen:
- bezeichnet die Infektionsrate
- bezeichnet den prozentualen Anteil der durch Tests erfassten Infizierten
- bezeichnet die Sterberate, mit der die Infizierten aus der Gesamtpopulation ausscheiden
Es gilt die Erhaltungsgleichung die besagt, dass sich die Gesamtpopulation um die verstorbenen Infizierten d*I verringert.
Es wird vorausgesetzt, dass Krankheitsverläufe teilweise symptomfrei verlaufen, d.h. dass nur ein Teil der Infizierten Krankheitssymptome aufweist. Dies hat zur Folge, dass auch nur ein Teil der tatsächlich Infizierten erfasst werden. Beispielsweise lässt sich durch den Faktor annehmen, dass lediglich 20% der tatsächlich Infizierten erfasst wurden. Mit und erhalten wir unser klassisches SIR-Modell. Das modifizierte SIR-Modell betrachtet nicht die allgemeine Populationsdynamik, die durch Neugeborene sowie Verstorbene ohne Zusammenhang mit einer Infektion.
Bearbeitung der Aufgabenstellung
[Bearbeiten]Das Ziel der Tutoriumsaufgabe 3 ist die Darstellung des Infektions- und Impfgeschehens mittels des modifizierten SIR-Modells. Hierfür wurde in einem ersten Schritt die jeweiligen Zahlen des Infektionsgeschehens in die bereits von Frau Hundertmark vorgefertigte Funktion "coronaData" implementiert, indem die jeweiligen Infektionszahlen in der Funktion ergänzt wurden. Die jeweiligen Werte konnte man aus dem Internet entnehmen. Vergleiche hierzu [[1]]
Anschließend erfolgt die Ermittelung einer geeigneten Basisinfektionsrate , die das exponentielle Wachstum des Infektionsgeschehens bis Ende April 2020 annäherend abbildet. Seit Beginn der Corona-Ausbreitung wächst die Anzahl der Infizierten bis Ende April 2020 (in unserem Fall konkret: die ersten 30 Tage) annäherend exponentiell, da keinerlei Gegenmaßnahmen zur Eindämmung des Infektionsgeschehen getroffen wurden. Es gibt zwei Möglichkeite, wie eine passende Basisinfektionsrate bestimmt werden könnte: anhand des Augenmaßes oder mittels der Regression.
Aufgabenstellung 1.1 - Bestimmung der Basisinfektionsrate mittels Augenmaß
[Bearbeiten]Zu Beginn der Pandemie, als die gesamte Bevölkerung uneingeschränkt empfänglich für eine Infizierung war, wurden noch keine gezielten Maßnahmen zum Schutz vor einer Infizierung getroffen, sodass das Infektionsgeschehen annähernd exponentiell wächst. Zur Bestimmung anhand des Augenmaßes einer geeignete Basisinfektionsrate c, die das exponentielle Wachstum bis Ende April 2020 gut abbildet, wurden unterschiedliche Werte für die Infektionsrate eingegeben und sich derart annähernd die gesuchte Variable c ermittelt.

%Aktuelle Daten der ersten 30 Tage beginnend vom 25.02.2020 bis zum 25.03.2020
timesWHO=[0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 ];
inf_falleWHO=[16 18 21 26 53 66 117 150 188 240 400 639 795 902 1139 1296 1567 2369 3062 3795 4838 6012 7156 8198 10999 13957 16662 18610 22672 27436 31554 ];
n=length(inf_falleWHO);
%Ermitteln der Basisinfektionsrate mittels Augenmaß
Infektionsrate=0.266;
Startwert=16; %Infizierte zum Zeitpunkt t=0
EndZeitpunkt=30; %wie viele Tage werden betrachtet
Tage=[1:1:EndZeitpunkt]; %Betrachtung bis 25.03.2020
f1=Startwert*exp(Infektionsrate*(Tage)); %definiere Exponentialfuktion
%Plotten des exponentiellen Wachstums und der echten Fälle
figure(1)
plot ( timesWHO, inf_falleWHO, '*r', Tage, f1, '-b');
title (['Infizierte Deutschland und Expo.-Funktion mit Infektiosnrate = '
num2str(Infektionsrate)]);
xlabel ('Tage ab dem 26. Februar 2020')
ylabel ('Personen')
grid on
axis([0, 30, 0 , 28000])
Nach mehreren Durchläufen wirkte die Infektionsrate 0,266 als kompatibelste annäherung der geplotteten Daten.

Aufgabenstellung 1.2 - Bestimmung der Basisinfektionsrate mittels der Regression
[Bearbeiten]Eine genauere Methode zur Findung der Basisinfektionsrate k ist das Verfahren der exponentiellen Regression [11]. Dabei ist es notwendig zu jedem Datenpunkt ein möglichst geringes Residuum zu finden, sodass die Abweichungen zu den ursprünglichen Daten möglichst minimiert wird. Damit lässt sich die Regressionskurve bestimmen.
%Aktuelle Daten der ersten 30 Tage beginnend vom 25.02.2020 bis zum 25.03.2020
timesWHO=[0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 ];
inf_falleWHO=[16 18 21 26 53 66 117 150 188 240 400 639 795 902 1139 1296 1567 2369 3062 3795 4838 6012 7156 8198 10999 13957 16662 18610 22672 27436 31554 ];
n=length(inf_falleWHO);
%geschätzter Anfangswert
a=70;
%geschätzte konstante (tägliche) Infektionsrate k∈[0,1]
k=0.16;
expon=@(t,k,a) a*exp(k.*t);
%Regression für die Wachstumsrate k den geschätzten Anfangswert a:
kopt=0;
res_vector=0;
a_vector=0;
MaxN=100;
%erste for-Schleife
for j=-MaxN/10:2*MaxN
aj=a+j*a*10/MaxN;
for i=-MaxN:MaxN
ki=k+i*k/MaxN;
res(i+MaxN+1)=norm ((expon(timesWHO,ki,aj)-inf_falleWHO),2);
if res(i+MaxN+1)==min(res)
Ind=i;
kopt= [kopt ki];
res_vector=[res_vector min(res)];
a_vector=[a_vector aj];
endif
endfor
resMatrix(j+MaxN/10+1,:)= res;
endfor
%zweite for-Schleife
for i=2:length(res_vector)
if res_vector(i)==min(res_vector(2:length(res_vector)))
Ind2=i;
endif
endfor
koptvec=kopt;
kopt=kopt(Ind2);
res_vector(Ind2);
a_vector(Ind2);
%optimale Wachstumsrate, Anfangswert und minmaler Fehler
Optim_Wachsrate=kopt
Optim_Anfangswert=a_vector(Ind2)
Optim_Residuum=res_vector(Ind2)
plot ( timesWHO,inf_falleWHO, 's', "linewidth",2 )
hold on
plot ( timesWHO, expon(timesWHO, kopt,Optim_Anfangswert), '-',"linewidth",3 );
set(gca,'xtick',[0,5,10,12,14,16,18,20, 22, 24,26,28,30,32, 34,36,38])
set(gca,'ytick',[0, 2500,5000,10000,15000,20000,25000 30000 40000 50000 60000 70000 80000 90000 100000])
grid on
resi= res_vector(Ind2);
xlabel('Tage')
legend ("RKI Daten", "exponentiele Regression")
title (['Infizierte Deutschland und Expo.-Funktion mit Infektiosnrate = '

Entsprechend erhalten wir eine optimale Wachstumsrate von k=0.1872 mit einem optimalen Anfangswert von 119 und einem optimalen Residiuum von 2794.1.
Aufgabenstellung 2.1: Erweitern und Plotten der Corona-Data Funktion/Datenbank
[Bearbeiten]Zunächst wurden die in der Corona-Data Funktion enthaltenen Daten mit den offiziellen Daten des RKIs bis zum 03.06.2021 erweitert. Diese werden jedoch unter einer externen coronaData_neu.m - Datei gespeichert:
%Aktuelle Daten vom 25.02.2020 bis 03.06.2021 function y= coronaData () infects = [ 16.0 18.0 21.0 26.0 53.0 66.0 117.0 150.0 188.0 240.0 400.0 639.0 795.0 902.0 1139.0 1296.0 1567.0 2369.0 3062.0 3795.0 4838.0 6012.0 7156.0 8198.0 10999.0 13957.0 16662.0 18610.0 22672.0 27436.0 31554.0 36508.0 42288.0 48582.0 52547.0 57298.0 61913.0 67366.0 73522.0 79696.0 85778.0 91714.0 95391.0 99225.0 103228.0 108202.0 113525.0 117658.0 120479.0 123016.0 125098.0 127584.0 130450.0 133830.0 137439.0 139897.0 141672.0 143457.0 145694.0 148046.0 150383.0 152438.0 154175.0 155193.0 156337.0 157641.0 159119.0 160758.0 161703.0 162496.0 163175.0 163860.0 164807.0 166091.0 167300.0 168531.0 169218.0 169575.0 170508.0 171306.0 172239.0 173152.0 173772.0 174355.0 174697.0 175210.0 176007.0 176752.0 177212.0 177850.0 178281.0 178570.0 179002.0 179364.0 179717.0 180458.0 181196.0 181482.0 181815.0 182028.0 182370.0 182764.0 183271.0 183678.0 183979.0 184193.0 184543.0 184861.0 185416.0 185674.0 186022.0 186269.0 186461.0 186839.0 187184.0 187764.0 188534.0 189135.0 189822.0 190359.0 190862.0 191449.0 192079.0 192556.0 193243.0 193499.0 193761.0 194259.0 194725.0 195228.0 195674.0 196096.0 196335.0 196554.0 196944.0 197341.0 197783.0 198178.0 198556.0 198804.0 198963.0 199375.0 199726.0 200260.0 200843.0 201372.0 201574.0 201823.0 202345.0 202799.0 203368.0 204183.0 204964.0 205269.0 205609.0 206242.0 206926.0 207828.0 208698.0 209653.0 209893.0 210402.0 211281.0 212022.0 213067.0 214214.0 215336.0 215891.0 216327.0 217293.0 218519.0 219964.0 221413.0 222828.0 223453.0 224014.0 225404.0 226914.0 228621.0 230048.0 232082.0 232864.0 233575.0 234853.0 236429.0 237936.0 239507.0 240986.0 241771.0 242381.0 243599.0 244855.0 246166.0 247619.0 248997.0 249985.0 250799.0 252298.0 253474.0 255366.0 256850.0 258480.0 259428.0 260355.0 261762.0 263663.0 265857.0 267773.0 270070.0 271415.0 272337.0 274158.0 275927.0 278070.0 280223.0 282730.0 284140.0 285332.0 287421.0 289219.0 291722.0 294395.0 296958.0 299237.0 300619.0 303258.0 306086.0 310144.0 314660.0 319381.0 322864.0 325331.0 329453.0 334585.0 341223.0 348557.0 356387.0 361974.0 366299.0 373167.0 380762.0 392049.0 403291.0 418005.0 429181.0 437866.0 449275.0 464239.0 481013.0 499694.0 518753.0 532930.0 545027.0 560379.0 577593.0 597583.0 619089.0 642488.0 658505.0 671868.0 687200.0 705687.0 727553.0 751095.0 773556.0 790503.0 801327.0 815746.0 833307.0 855916.0 879564.0 902528.0 918269.0 929133.0 942687.0 961320.0 983588.0 1006394.0 1028089.0 1042700.0 1053869.0 1067473.0 1084743.0 1106789.0 1130238.0 1153556.0 1171323.0 1183655.0 1197709.0 1218524.0 1242203.0 1272078.0 1300516.0 1320716.0 1337078.0 1351510.0 1379238.0 1406161.0 1439938.0 1471238.0 1494009.0 1510652.0 1530180.0 1554920.0 1587115.0 1587115.0 1627103.0 1640858.0 1651834.0 1664726.0 1687185.0 1719737.0 1719737.0 1755351.0 1765666.0 1775513.0 1787410.0 1808647.0 1835038.0 1866887.0 1891581.0 1908527.0 1921024.0 1933826.0 1953426.0 1978590.0 2000958.0 2019636.0 2033518.0 2040659.0 2052028.0 2068002.0 2088400.0 2106262.0 2122679.0 2134936.0 2141665.0 2148077.0 2161275.0 2178828.0 2192850.0 2205171.0 2216363.0 2221971.0 2228085.0 2237790.0 2252001.0 2264909.0 2275394.0 2284010.0 2288545.0 2291924.0 2299996.0 2310233.0 2320093.0 2328447.0 2334561.0 2338987.0 2342843.0 2350399.0 2360606.0 2369719.0 2378883.0 2386559.0 2390928.0 2394811.0 2402818.0 2414687.0 2424684.0 2434446.0 2442336.0 2447068.0 2451011.0 2460030.0 2471942.0 2482522.0 2492079.0 2500182.0 2505193.0 2509445.0 2518591.0 2532947.0 2545781.0 2558455.0 2569245.0 2575849.0 2581329.0 2594764.0 2612268.0 2629750.0 2645783.0 2659516.0 2667225.0 2674710.0 2690523.0 2713180.0 2734753.0 2755225.0 2772401.0 2782273.0 2791822.0 2808873.0 2833173.0 2855061.0 2873190.0 2885386.0 2893883.0 2900768.0 2910445.0 2930852.0 2956316.0 2980413.0 2998268.0 3011513.0 3022323.0 3044016.0 3073442.0 3099273.0 3123077.0 3141262.0 3153699.0 3163308.0 3188192.0 3217710.0 3245253.0 3268645.0 3287418.0 3299325.0 3310301.0 3332532.0 3357268.0 3381597.0 3400532.0 3416822.0 3425982.0 3433516.0 3451550.0 3473503.0 3491988.0 3507673.0 3520329.0 3527251.0 3533376.0 3548285.0 3565704.0 3577040.0 3584934.0 3593434.0 3598846.0 3603055.0 3614095.0 3626393.0 3635162.0 3642244.0 3648958.0 3651640.0 3653551.0 3656177.0 3662490.0 3669870.0 3675296.0 3679148.0 3681126.0 3682911.0 3687828.0]; deads = [ 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 12.0 20.0 31.0 46.0 55.0 86.0 114.0 149.0 198.0 253.0 325.0 389.0 455.0 583.0 732.0 872.0 1017.0 1158.0 1342.0 1434.0 1607.0 1861.0 2107.0 2373.0 2544.0 2673.0 2799.0 2969.0 3254.0 3569.0 3868.0 4110.0 4294.0 4404.0 4598.0 4879.0 5094.0 5321.0 5500.0 5640.0 5750.0 5913.0 6115.0 6288.0 6481.0 6575.0 6649.0 6692.0 6831.0 6996.0 7119.0 7266.0 7369.0 7395.0 7417.0 7533.0 7634.0 7723.0 7824.0 7881.0 7914.0 7935.0 8007.0 8090.0 8147.0 8174.0 8216.0 8247.0 8257.0 8302.0 8349.0 8411.0 8450.0 8489.0 8500.0 8511.0 8522.0 8551.0 8581.0 8613.0 8646.0 8668.0 8674.0 8711.0 8729.0 8755.0 8763.0 8781.0 8787.0 8791.0 8800.0 8830.0 8856.0 8872.0 8883.0 8882.0 8885.0 8895.0 8914.0 8927.0 8948.0 8954.0 8957.0 8961.0 8973.0 8985.0 8994.0 9003.0 9010.0 9012.0 9016.0 9024.0 9036.0 9048.0 9054.0 9060.0 9063.0 9064.0 9068.0 9071.0 9078.0 9082.0 9083.0 9084.0 9086.0 9090.0 9095.0 9101.0 9111.0 9118.0 9118.0 9118.0 9122.0 9128.0 9134.0 9141.0 9148.0 9141.0 9148.0 9156.0 9168.0 9175.0 9183.0 9195.0 9196.0 9197.0 9201.0 9207.0 9211.0 9225.0 9231.0 9231.0 9232.0 9236.0 9243.0 9253.0 9260.0 9267.0 9269.0 9272.0 9277.0 9280.0 9285.0 9288.0 9289.0 9295.0 9298.0 9302.0 9313.0 9321.0 9322.0 9324.0 9325.0 9325.0 9329.0 9338.0 9341.0 9342.0 9347.0 9349.0 9350.0 9362.0 9368.0 9371.0 9378.0 9384.0 9386.0 9386.0 9396.0 9409.0 9428.0 9443.0 9452.0 9457.0 9460.0 9471.0 9488.0 9500.0 9508.0 9527.0 9529.0 9534.0 9546.0 9562.0 9578.0 9589.0 9604.0 9615.0 9621.0 9634.0 9677.0 9710.0 9734.0 9767.0 9777.0 9789.0 9836.0 9875.0 9905.0 9954.0 10003.0 10032.0 10056.0 10098.0 10183.0 10272.0 10349.0 10452.0 10481.0 10530.0 10661.0 10812.0 10930.0 11096.0 11226.0 11289.0 11352.0 11506.0 11767.0 11982.0 12200.0 12378.0 12485.0 12547.0 12814.0 13119.0 13370.0 13630.0 13884.0 14022.0 14112.0 14361.0 14771.0 15160.0 15586.0 15965.0 16123.0 16248.0 16636.0 17123.0 17602.0 18034.0 18517.0 18772.0 18919.0 19342.0 19932.0 20372.0 20970.0 21466.0 21787.0 21975.0 22475.0 23427.0 24125.0 24938.0 25640.0 26049.0 26275.0 27006.0 27968.0 28770.0 28770.0 29422.0 29778.0 30126.0 30978.0 32107.0 33071.0 33071.0 33960.0 34272.0 34574.0 35518.0 36537.0 37607.0 38795.0 39878.0 40343.0 40686.0 41577.0 42637.0 43881.0 44994.0 45974.0 46419.0 46633.0 47622.0 48770.0 49783.0 50642.0 51521.0 51870.0 52087.0 52990.0 53972.0 54913.0 55752.0 56546.0 56945.0 57120.0 57981.0 58956.0 59742.0 60597.0 61286.0 61517.0 61675.0 62156.0 62969.0 63635.0 64191.0 64742.0 64960.0 65076.0 65604.0 66164.0 66698.0 67206.0 67696.0 67841.0 67903.0 68318.0 68740.0 69125.0 69519.0 69888.0 70045.0 70105.0 70463.0 70881.0 71240.0 71504.0 71804.0 71900.0 71934.0 72189.0 72489.0 72810.0 73062.0 73301.0 73371.0 73418.0 73656.0 73905.0 74132.0 74358.0 74565.0 74664.0 74714.0 74964.0 75212.0 75440.0 75623.0 75780.0 75870.0 75913.0 76093.0 76342.0 76543.0 76775.0 76895.0 76963.0 77013.0 77103.0 77401.0 77707.0 78003.0 78249.0 78353.0 78452.0 78746.0 79088.0 79381.0 79628.0 79847.0 79914.0 80006.0 80303.0 80634.0 80893.0 81158.0 81444.0 81564.0 81624.0 81968.0 82280.0 82544.0 82850.0 83082.0 83192.0 83276.0 83591.0 83876.0 84126.0 84410.0 84648.0 84775.0 84829.0 85112.0 85380.0 85658.0 85848.0 86025.0 86096.0 86160.0 86381.0 86665.0 86902.0 87128.0 87298.0 87380.0 87423.0 87456.0 87726.0 87995.0 88187.0 88350.0 88406.0 88442.0 88595.0 88774.0]; recovered = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 13500.0, 16100.0, 18700.0, 21400.0, 23800.0, 26400.0, 28700.0, 30600.0, 33000.0, 46300.0, 49000.0, 53913.0 57400.0 60200.0 64300.0 68200.0 72600.0 77000.0 81800.0 85400.0 88000.0 91500.0 95200.0 99400.0 103300.0 106800.0 109800.0 112000 114500 117400.0 120400.0 123500.0 126900.0 129000.0 130600.0 132700.0 135100.0 137400.0 139900.0 141700.0 143300.0 144400.0 145600.0 147200.0 148700.0 150300.0 151700.0 152600.0 153400.0 154600.0 155700.0 156900.0 158000.0 159000.0 159900.0 160300.0 161200.0 162000.0 162800.0 163200.0 164100.0 164900.0 165200.0 165900.0 166400.0 167300.0 167800.0 168500.0 168900.0 169100.0 169600.0 170200.0 170700.0 171200.0 171600.0 171900.0 172200.0 172600.0 173100.0 173600.0 174100.0 174400.0 174700.0 174900.0 175300.0 175700.0 176300.0 176800.0 177100.0 177500.0 177700.0 178100.0 179100.0 179800.0 180300.0 181000.0 181300.0 181700.0 182200.0 182700.0 183100.0 183600.0 184000.0 184400.0 184600.0 185100.0 185500.0 186000.0 186400.0 186900.0 187200.0 187400.0 187800.0 188100.0 188600.0 189000.0 189400.0 189800.0 190000.0 190400.0 190800.0 191300.0 191800.0 192300.0 192700.0 192900.0 193500.0 194000.0 194600.0 195200.0 195900.0 196400.0 196800.0 197400.0 198100.0 198800.0 199500.0 200200.0 200800.0 201300.0 202100.0 203000.0 203900.0 204800.0 205800.0 206600.0 207100.0 208200.0 209300.0 210600.0 211900.0 213200.0 214200.0 214900.0 216200.0 217600.0 219100.0 220500.0 221900.0 222900.0 223700.0 225000.0 226500.0 228000.0 229400.0 230600.0 231400.0 232100.0 233300.0 234600.0 236000.0 237300.0 238700.0 239800.0 240700.0 242200.0 243700.0 245400.0 246900.0 248500.0 249700.0 250500.0 252500.0 254200.0 256000.0 257900.0 259500.0 260900.0 261900.0 263700.0 265600.0 267700.0 269600.0 271800.0 273500.0 274800.0 276900.0 279300.0 281900.0 284600.0 287600.0 290000.0 291900.0 294800.0 298300.0 302100.0 306100.0 310300.0 314100.0 317100.0 321600.0 326700.0 332800.0 339200.0 345700.0 351200.0 355900.0 363100.0 371500.0 381400.0 391600.0 402500.0 412000.0 419300.0 429600.0 441200.0 454800.0 467800.0 481700.0 493200.0 502300.0 515200.0 530200.0 546500.0 562700.0 579100.0 593100.0 603800.0 618800.0 636700.0 656400.0 676100.0 696100.0 711000.0 722300.0 739100.0 758800.0 779500.0 800000.0 820600.0 835700.0 846400.0 863300.0 881800.0 902100.0 922100.0 942100.0 957500.0 967900.0 984200.0 1003300.0 1025000.0 1047600.0 1069400.0 1085500.0 1097400.0 1115400.0 1136700.0 1160100.0 1184400.0 1184400.0 1223700.0 1236700.0 1255700.0 1277900.0 1302600.0 1328200.0 1328200.0 1368100.0 1381900.0 1401200.0 1424700.0 1451000.0 1474000.0 1494100.0 1511800.0 1525300.0 1545500.0 1570000.0 1596600.0 1620200.0 1641200.0 1657900.0 1672000.0 1691700.0 1716200.0 1741800.0 1762200.0 1780200.0 1795400.0 1807500.0 1823500.0 1844000.0 1866000.0 1883700.0 1898900.0 1911800.0 1921700.0 1935600.0 1954000.0 1973200.0 1991000.0 2008200.0 2020900.0 2029200.0 2041300.0 2057300.0 2073100.0 2087600.0 2101000.0 2112000.0 2119100.0 2128800.0 2141400.0 2154600.0 2165900.0 2176300.0 2185100.0 2190600.0 2198000.0 2207700.0 2217700.0 2226500.0 2235700.0 2243200.0 2248400.0 2255500.0 2264600.0 2274400.0 2283400.0 2292100.0 2299400.0 2304300.0 2310900.0 2319600.0 2328700.0 2337000.0 2345600.0 2352600.0 2358000.0 2365100.0 2374200.0 2383600.0 2392600.0 2401700.0 2409700.0 2415200.0 2423400.0 2433800.0 2445300.0 2456200.0 2467600.0 2477500.0 2484600.0 2494800.0 2507900.0 2521800.0 2535000.0 2548200.0 2560400.0 2569400.0 2581500.0 2597100.0 2614500.0 2631400.0 2647600.0 2661500.0 2671200.0 2683900.0 2700200.0 2718700.0 2736100.0 2752000.0 2765100.0 2775200.0 2787200.0 2803600.0 2824100.0 2845300.0 2865000.0 2882300.0 2893900.0 2910100.0 2931400.0 2954000.0 2975200.0 2995200.0 3012100.0 3024600.0 3040700.0 3061500.0 3084700.0 3107300.0 3128800.0 3147100.0 3159200.0 3175600.0 3196900.0 3220300.0 3240300.0 3259000.0 3275500.0 3286400.0 3300700.0 3320300.0 3340400.0 3358000.0 3374600.0 3387800.0 3397100.0 3408800.0 3423700.0 3438800.0 3450400.0 3461700.0 3471800.0 3478600.0 3486700.0 3498400.0 3509600.0 ]; y=[infects;deads;recovered]; endfunction
Anschließend erfolgt die Implementierung der gesammelten Corona-Daten:
%Parameter des SIR Models
NM=55000 % Kapazitätsgrenze, 2/3 der deutschen Befölkerung (In T)
c=0.1872 %Basisinfektionsrate- die Rate des exponenziellen Wachstums am Anfang der Pandemie (vgl. Aufgabe 1.2)
w=1/13.90; % Wechselrate zu den Genesenen
d=0.003 % Todesrate
%Anteil der erfassten Infizierten
r=0.1
%Implementierung der gesammelten Corona-Daten
A=coronaData_neu();
inf_falleWHO=A(1,:);
inf_falleWHOrecovered=A(3,:);
inf_falleWHOtoten=A(2,:);
inf_falleWHOaktuell=inf_falleWHO-inf_falleWHOrecovered; % Infizierten - Genesene ergeben die aktuellen Infizierten
n=length(inf_falleWHO) %wichtig, Vektoren benötigen die gleiche Länge
timesWHO=[0:1:n-1];
%Plotten der Grafik
figure(1)
title ('Corona- infizierten Detuschland, Quelle RKI')
plot (timesWHO, inf_falleWHO./1000, 'markersize', 1, 's', "linewidth",4, timesWHO,inf_falleWHOaktuell/1000,'markersize', 1, '*' , timesWHO,inf_falleWHOrecovered/1000,'markersize', 1,'s', timesWHO, inf_falleWHOtoten./1000 ,'markersize', 1, '*' ) %durch 1000 teilen, da die Daten absolute Zahlen sind
xlabel ('Tage vom 26. Februar')
ylabel ('Zahlen in Tausend')
legend ( "German data I +R" ,"German data I ","German data R", "German data deaths" ,"location", "north")
grid on
xticks([50,100,150,200,250,300,350,400,450,500])
axis([0,n, 0 ,4000])
Diese CoronaDatenbank wird anschließend geplottet:

Anahnd der Grafik ist das vergangene Infektionsgeschehen und die Auswirkungen der getroffenen Maßnahmen im Zeitraum vom 25.02.2020 bis zum 03.06.2021 erkennbar. Beispielsweise lässt sich ein Hochpunkt der Infektionen nach ungefähr 300 Tagen erkennen, also ungefähr um die Weihnachtszeit des Jahres 2020. Der anschließende Abfall deckt sich widerum ungefähr mit der Verschärfung der Regelungen und einem sich ständig verlängernden Lockdown. Ende Februar steigen die Zahlen wieder langsam an bis zum nächsten Peak ungefährt Mitte/Ende April bevor die Kurve abermals anfängt zu sinken. Den erneuten Anstieg der Zahlen kann man mit dem Auftreten der stärker infizierenden Mutation erklären. Zeitgleich steigt jedoch auch die Zahl der Geimpften und der Tests an: Ab Anfang März 2021 können sich alle Bürgerinnen und Bürger kostenlos in Testzentren auf eine Coronainfektion testen lassen. Die Notbremse über Ostern im April leistet ihren Beitrag zur Eindämmung der Infektion. [12]
Aufgabenstellung 2.2: Das klassische vs. modifizierte SIR-Modell
[Bearbeiten]Das Infektionsgeschehen im klassischen SIR-Modell
In einem nächsten Schritt wird das Infektionsgeschehen mittels eines SIR-Modells dargestellt. Dabei verwenden wir die in Aufgabe 1.2 ermittelte Infektionsrate c = 0.1872. Zunächst werden dabei die festen Parameter festgelegt: Ausgehend von einer Kapazität von 55'000= (ungefähr zwei Drittel von 80'000), der Infektionsrate c = 0.1872 und einer Genesungsrate von 1/14 wird das SIR-Modell für den Zeitraum von 465 Tagen, also vom 25.02.2020 bis zum 03.06.2021 konstruiert:
%Parameter des SIR-Models NM=55000 % Kapazitätsgrenze, 2/3 der deutschen Bevölkerung (In T) c=0.1872 %Basisinfektionsrate- die Rate des exponenziellen Wachstums am Anfang der Pandemie w=1/14; % Wechselrate zu den Genesenen time=(0:1:465) Anfangsinfizierte=16/1000 %Anteil der erfassten Infizierten Anfangsgenesene=0 %Spaltenvektor: S, I, R zu Beginn der Pandemie y0=[NM-Anfangsinfizierte; Anfangsinfizierte; Anfangsgenesene]
Für das klassische SIR-Modell folgt nun in einem nächsten Schritt die Implementierung der rechten Seite des Differentialgleichungssystems. Prinzipiell gehen wir zunächst von einer konstanten Gesamtbevölkerung aus.. Da weder Personen hinzugefügt, noch entfernt werden, gilt folgende Gleichung: , wobei N für die Größe der Population steht. Somit erhält man folgende Funktionen, die für die Funktion des Differentialgleichungssystems implementiert werden:
Somit erhält man das nachfolgende Differentialgleichungssystem. Zum Schluss wird das noch als Grafik ausgegeben:
f=@(y,x) [-c*y(1)*y(2)/NM; +c*y(1)*y(2)/NM-w*y(2); +w*y(2)];
y=lsode(f, y0, time)
figure (2)
plot(time, y (:,1), '-', time, y (:,2),'-', time, y (:,3), '-', time, y (:,3)+ y (:,2),'-')
legend ("Empfaengliche", "Infizierte", "Genesene/Tote", "kumulierte Infizierte", "location", "east")
axis([0 465 0 56000])

Das Infektionsgeschehen im modifizierten SIR-Modell
Es gilt nun:
- :
- :
- :,
- :
mit
- ist die Infektionsrate
- beschreibt die Wechselrate von der Gruppe der Infizierten in die Gruppe der Genesenen bzw. der Toten
- steht für die Todesrate.
- entspricht dem Perzentualanteil der durch Tests erfassten Infizierten (Erkrankten) .
Zudem gilt das Erhaltungsgesetz .
Nun muss zusätzlich der Wert r festgelegt werden.
%Parameter des SIR-Models
NM=55000 % Kapazitätsgrenze, 2/3 der deutschen Befölkerung (In T)
c=0.1872 %Basisinfektionsrate- die Rate des exponenziellen Wachstums am Anfang der Pandemie
w=1/14; % Wechselrate zu den Genesenen
d=0.003 %Todesrate
time=(0:1:465)
Anfangsinfizierte=16/1000 %Anteil der erfassten Infizierten
Anfangsgenesene=0
r=0.15 %konstanten Faktor, der den prorzentualen Anteil, der durch Tests erfassten Infizierten (Erkrankten) beschreibt
Anfangstote=0
y0=[NM-Anfangsinfizierte; Anfangsinfizierte; Anfangsgenesene; Anfangstote]
% Funktion f der rechten Seite des DGL-Systems y'=f(y,t)
f=@(y,x) [-c*y(1)*y(2)/(NM*r); + c*y(1)*y(2)/NM - w*y(2); w*y(2)-d*y(2); d*y(2)];
y=lsode(f, y0, time);
figure (3)
plot(time, y (:,1), '-', time, y (:,2),'-', time, y (:,3), '-', time, y (:,3)+ y (:,2),'-', time, y (:,4), '-')
title (['mod. SIR-Model mit r=' num2str(r)]);
legend ("Empfaengliche", "Infizierte", "Genesene", "kumulierte Infizierte", "Tote", "location", "east")
axis([0 465 0 56000])
xlabel ('Tage')
ylabel ('Bevoelkerung (in Tausend)')
Nach dem Plotten erhalten wir dann die nachfolgende Grafik:

Einschub: Aufgabenstellung 3 - Auswirkungen Veränderung Parameter r
Der Vergleich mit unterschiedlichen Abbildungen des SIR-Modells verdeutlicht die Rolle des Parameters r: je kleiner r gewählt wird, desto weniger tatsächlich infizierte Personen werden erfasst. Das bedeutet, dass eine hohe Dunkelziffer an nicht erkannten Infektionen existiert. Im Umkehrschluss bedeutet das aber auch, dass bei mehr Menschen falsch-positiv getestet wurden. Ist jedoch , so wurden alle Infizierten erfasst und es liegt das klassische SIR-Modell vor. Die nachfolgende Simulation verdeutlicht das SIR-Modell für unterschiedliche r-Werte:

Setzt man dieses Wissen mit den realen Gegebenheiten in Verbindung, so wird deutlich, dass zu Beginn der Pandemie ein kleiner r-Wert vorlag: Die Dunkelziffer nicht erkannter Infektionen war aufgrund mangelnder und stark eingeschränkter Testmöglichkeiten hoch, sodass Infizierte mit schwachen oder gar keinen Symptomen unentdeckt bleiben konnten.
Aufgabenstellung 2.3: Die Verlangsamungsfunktion/Slowdown-Funktion
[Bearbeiten]Um die Slowdown-Funktion approximieren zu können, weden zunächst die realen Werte des RKIs mit den Daten des modifizierten SIR-Modells verglichen. Hierfür werden in einem ersten Schritt beide Daten in einer Abbildung dargestellt und anschließend die Kurven miteinander verglichen.

Mit Hilfe der Slowdown-Funktion sollen die modellierten Kurven derart verändert werden, dass sie den breiteren Kurven entsprechen. Hierfür sind jedoch einige Informationen des bisherigen epidemiologischen Verlaufs notwendig: Zu Beginn der Pandemie stiegen die Werte der Infizierten exponentiell an, da die Entwicklung der Epidemie unterschätzt wurde und es nur wenige beziehungsweise keine Maßnahmen umgesetzt wurden. Ab dem 16. März 2020 wurde der erste Lockdown umgesetzt (ab dem 21. Tag), was sich natürlich auch etwas verzögert auf die Ausbreitung der Infizierung auswirkte (ab ca dem 35. Tag). Die nächsten Monate wurden weitere Maßnahmen ergriffen, unter anderem die Abstandsregelungen, die verschärfte Maskenpflicht aber auch die Kontaktbeschränkungen. Mit dem Beschluss vom 6. Mai 2020 (Tag 72 nach Pandemiebeginn) erhielten die Länder weitgehend die Verantwortung für weitere Lockerungen. Ab August/September (um den Tag 175 - 190) fand der Unterricht (nach den Sommerferien) wieder regulär im Präsenz statt, die Kontaktbeschränkungen werden gelockert. Infolgedessen stiegen die Zahlen der Neuinfektionen zeitnah wieder an, sodass ab dem 02.November 2020 (Tag 252) zunächst wieder veschärfte Maßnahmen und ein Lockdown light in Kraft trat, der kurz darauf später (Tag 275) abermals verschärft wurde. "Bürger wurden aufgefordert, soziale Kontakte auf ein absolutes Minimum zu reduzieren und der Aufenthalt in der Öffentlichkeit wurde auf kleine Gruppen beschränkt. Zahlreiche Einrichtungen wurden erneut geschlossen: Dazu gehörten Kultur-, Gastronomie- und Dienstleistungsbetriebe. Geöffnet blieben Schulen, Kindergärten und Groß- und Einzelhandelsbetriebe. [...] Die Pflicht zum Tragen einer Maske im öffentlichen Raum wurde weiter ausgedehnt."[13] Der gewünschte Effekt blieb jedoch aus, sodass aufgrund der weiterhin hohen Infektionszahlen ab dem 16. Dezember 2020 bis zum 10. Januar 2021 (Tag 296 - 312) die Infektionsschutzmaßnahmen mit einem zweitem Lockdown abermals verschärft wurden. Dies hat zur Folge, dass um die Weihnachtszeit die Zahlen abermals zu sinken beginnen. Knapp ein Jahr nach dem Ausbruch der Pandemie steigt die Anzahl der Infizierten erneut rasant an. Das Auftreten der britischen Variante erklärt den verstärkten Anstieg, sodass daraufhin die Bundesnotbremse und die ersten Erfolge der Impfkampagne dazu führen, dass nach kurzer Zeit die Zahl der Neuinfektionen wieder fällt.[14]
All diese Auswirkungen werden nun anhand des Parameters r in eine Funktion implementiert:
function Wert=slowdown(x);
if x<30
Wert=1.7;
elseif x<34
Wert=1.3;
elseif x<43
Wert=0.5;
elseif x<100
Wert=0.25;
elseif x<200
Wert=0.4;
elseif x<300
Wert=0.55;
elseif x<377
Wert=0.35;
elseif x<440
Wert=0.45;
else
Wert=0.3;
endif
endfunction
%Funktion slowdown einfügen und numerisch mittels Octave lösen lassen
for i=length (time)
Faktor_slowdown(i)=slowdown(i);
endfor
r=1;
f=@(y,x) [-c*slowdown(x)*y(1)*y(2)/(NM*r); +c*slowdown(x)*y(1)*y(2)/NM-w*y(2); +w*y(2)-d*y(2); d*y(2)];
y=lsode(f, y0, time);
%Plotten der Grafik
figure(22)
plot (timesWHO, inf_falleWHO/1000, '*c', timesWHO,inf_falleWHOaktuell/1000, '*r' , timesWHO, inf_falleWHOrecovered/1000,'*g', time, y (:,2),'r-', time, y (:,3), 'g-', time, y (:,3)+ y (:,2),'c-')
title ('Vergleich RKI mit Model')
xlabel ('Tage ab dem 26. Februar')
ylabel ('Zahlen in Tausend')
legend ( "kumulierte Infizierte (RKI)" ,"aktuell Infizierte (RKI)","genesen/imun (RKI)" , "Infizierte (Model)", "Genesene (Model)", "kumulierte Inzizierte (Model)", "location", "north")
grid on
axis([0,n,0,2000])
Das ergibt folgende Abbildung. Man sieht, dass das Modell mit Hilfe der slowdown-Funktion das modifizierte SIR-Modell (ausreichend) gut an die aktuellen Daten des RKIs annähert:


Der Vergleich der tatsächlichen mit der slowdown Infektionsrate ergibt mit den folgenden Befehlen die folgende Grafik:
%Slowdown-Funktion
for i=1:length(timesWHO)
cc(i)=slowdown (timesWHO (i) );
endfor
plot (timesWHO,cc)
hold on
%infektionsrate aus den RKI-Daten berechnet:
T=1
ccc(1)=cc(1);
for i=T+1:n
ccc(i-T)=(inf_falleWHO(i)-inf_falleWHO(i-T))/(inf_falleWHO(i-T));
% Infektionsrate aus dem beschränktem Modell
ccc2(i-T)=NM*(inf_falleWHO(i)-inf_falleWHO(i-T))/(inf_falleWHO(i-T)*(NM-0.001*inf_falleWHO(i-T)));
endfor
% Plot
x=0:1:500;
for i=1:1:length(x)
vec2(i)=slowdown(x(i));
endfor
plot(x,vec2)
plot (ccc, 'markersize', 0.5, '*', ccc2,'markersize', 0.5, 's')
grid on
title ('Tatsaechtliche und slowdown Infektionsrate')
legend ('slowdown Funktion', 'Infektionsrate c-Data' )
hold on
Man erkennt, dass die tatsächliche und die slowdown Infektionsrate doch sehr unterschiedlich sind. Das kommt auch bei der näheren Betrachtung des relativen Fehlers:

%zum Vergleich relativer Fehler der Infektionsraten aus beschänkten und unbeschränktem Modell
plot (abs(ccc-ccc2)./ccc)
%plot (NM-0.001*inf_falleWHO(2:length(timesWHO))) % Kapazität
title ('Relat Fehler der tatsaechlichen und slowdown Infektionsrate')
Numerische Lösung des SIR -Systems
Die Octave Funktion 'lsode' löst ein System gewöhnlicher Differentialgleichungen mit adequaten numerischen Methoden. 'lsode' übernimmt als Parameter den Namen der Funktion f der rechten Seite des System der gewönlicher Differentialgleichungen:
mit dem Anfangsvektor: und dem Vektor der Zeitschritte in den die Lösung berechnet werden sollte.

%Lösung des ODE Systems times=(0:0.1:465); %Anfangsbedingungen yo=[NM-16/1000;16/1000;0]; f=@(y,x) [-c*slowdown(x,25)*y(1)*y(2)/(r*NM);c*slowdown(x,25)*y(1)*y(2)/NM-w*y(2);w*y(2)-0*y(2)]; y = lsode (f, yo, times); %Grafikausgabe: figure(2) plot ( times, y (:,2), '.', times, y (:,3),'.',times, y (:,3)+y (:,2),'.') hold on plot (timesWHO, inf_falleWHO./1000, 's', "linewidth",4, timesWHO,inf_falleWHOaktuell/1000, '*' , timesWHO,inf_falleWHOrecovered/1000, '*' ) legend ( "Infected", "Removed", " Infected+Removed","German data I +R" ,"German data I ","German data R" ,"location", "west") axis([0,n, 0 ,2200])
Man erkennt, dass trotz einer guten Annäherung der Infiziertenzahlen die modellierte Zahlen der Genesenen deutlich von den Daten abweichen. Ferner musste die slowdown-Funktion weniger an die Daten der Infektionsrate als an die Infektionszahlen selbst angepasst werden. Kleine Änderungen in der slowdown Funktion führen somit zu großen änderungen in den modellierten Infektionszahlen. Wie folgt kann man sich den Fehler der Modellierung noch anzeigen lassen: Die nachfolgenden Befehle zeigen, wie man sich den Fehler der Modellierung anzeigen lassen kann:

%relat. Fehler Infizierte
%Interpolation der Funktionswerte an die RKI-Zeiten (Tage)
I=interp1 (times, y(:,2), timesWHO+1);
abs_I=abs(I-inf_falleWHOaktuell/1000);
rel_I=abs(I-inf_falleWHOaktuell/1000)./(inf_falleWHOaktuell/1000);
plot (timesWHO, rel_I)
title ('relativer Fehler, Infected , Recovered')
hold on
%Fehlermaß
maas_I=norm(abs_I)/norm(inf_falleWHOaktuell/1000)
%weiterer Fehlermaß Durchschnitt und Euklid-Norm
rel_I_mean=mean(rel_I)
rel_I_norm=norm(rel_I);
%relat. Fehler Genesene/Toten
R=interp1 (times, y(:,3), timesWHO+1);
abs_R=abs(R-inf_falleWHOrecovered/1000);
rel_R=abs(R-inf_falleWHOrecovered/1000)./(inf_falleWHOrecovered/1000);
plot (timesWHO, rel_R, '*')
hold off
legend('Infected', 'Recovered')
%Fehlermaß
maas_R=norm(abs_R)/norm(inf_falleWHOrecovered/1000)
% weiterer Fehlermaß: Durchschnitt und Euklid-Norm
rel_R_mean=mean(rel_R(36:length(timesWHO)))
rel_R_norm=norm(rel_R(36:length(timesWHO)));
Aufgabenstellung 4: Berücksichtigung der Impfungen (unvollständig)
[Bearbeiten]
In einem letzten Schritt sollen nun die Auswirkungen der Impfungen berücksichtigt werden. Um dies umsetzen zu können, werden zunächst die offiziellen Impfdaten der Bundesregierung in einer neuen Funktion ImpfData gesammelt. Am 26. Dezember 2020 haben die COVID-19-Impfungen in Deutschland begonnen, und ab dem 14. Januar 2021 bekamen die ersten Personen ebenfalls ihre zweite Impfdosis. Die Grafik[15] links stellt die Entwicklung der Gesamtanzahl der Personenseit Impfbeginn dar, welche die Erst- und die vollständige Impfung erhalten haben. Da erst zwei Wochen nach der Zweitimpfung ein optimaler Schutz gewährleistet werden kann wurden lediglich die Daten zu den Zweitimpfungen betrachtet[16]. Dementsprechend wurden in der neuen Funktion ImpfData die veabreichten Impfdaten ab Tag 312 (15.01.2021) eingetragen, die jedoch erst ab Tag 324 (29.01.2021) einen Einfluss auf unser Modell hat.
Impfungen=[ 0 0.610 0.906 17.362 15.771 34.964 51.584 41.907 35.559 44.959 23.147 38.685 48.439 59.638 46.098 57.646 52.167 30.533 61.486 67.732 95.445 70.776 77.174 53.065 26.096 56.783 74.221 76.798 67.443 76.095 45.579 25.265 55.632 54.694 55.776 51.296 54.841 37.115 29.107 60.108 59.759 59.583 58.507 65.425 40.029 24.285 49.384 53.698 69.059 62.836 67.409 49.305 34.462 52.505 54.742 65.745 60.894 71.717 49.439 35.993 58.894 67.036 79.509 75.353 82.847 53.862 38.762 76.189 83.513 88.191 80.002 88.656 63.177 52.750 89.034 93.359 103.115 92.615 71.658 66.012 53.518 73.375 99.281 97.184 89.794 88.768 65.551 50.020 76.911 73.605 83.524 71.035 75.368 56.518 39.188 60.850 61.886 71.919 66.335 67.946 59.851 47.866 73.340 90.484 127.377 132.811 137.762 76.382 67.960 116.008 162.431 227.883 219.748 231.902 154.720 103.519 192.554 284.650 362.851 159.407 230.327 164.932 122.007 204.786 355.842 533.059 487.112 436.746 258.427 159.531 181.350 377.132];
In einem ersten Schritt wurden nur die Impfdaten in einer Grafik ausgegeben. Diese wurde mit dem Befehl des gleitenden Durchschnitts zunächst geglättet, um Schwankungen auszugleichen, die aufgrund von geringeren Impfzahlen am Wochenende zustande kommen.

x=334:465; v1=Impfungen v=v1.*0.001; plot(x,v) hold on M=movmean(v,20); plot(x,M) hold off
Anschließend betrachtet man die Auswirkungen der Impfungen auf die Gruppe der Empfänglichen: Hierfür verleicht man die Kurve der Empfänglichen ohne Impfungen mit der Kurve der Empfänglichen unter Berücksichtigung der Impfungen. Dabei nehmen wir einige Annahmen vor: 1. Geimpfte können sich (vorerst) nicht mehr infizieren. 2. Die Impfwirksamkeit beträgt 90%. Das bedeutet, dass bei 10% der Geimpften kein ausreichender Schutz gegen eine mögliche Infektion besteht. Diese Personen werden folglich nicht von der Gruppe der Empfänglichen abgezogen, da sie infiziert werden können.
Die Befehle hierfür könnten so aussehen:
%Parameter des SIR Models
NMV=83000 %Anzahl der Gesamtbevlkerung in T
c=0.1872 %Basisinfektionsrate- die Rate des exponenziellen Wachstums am Anfang der Pandemie
w=1/13.90; % Wechselrate zu den Genesenen
d=0.003 % Todesrate
%Anteil der erfassten Infizierten
r=0.1
B=ImpfDataneu();
people=B(1,:); % die erste Zeile der Matrix wird "people" genannt, Einträge immer 83000
Infizierte=B(2,:); % die zweite Zeile der Matrix wird "Infizierte" genannt
Impfungen=B(3,:); % die dritte Zeile der Matrix wird "Impfungen" genannt
Impfwirksamkeit=0.9;
Empfaengliche=people-(Infizierte); %Anzahl der Empfängliche ohne Impfstoff ergibt sich aus der Differenz der Gesamtbevölkerung und den bereits Infizierten
EmpfaenglicheMitImpfung=people-(Infizierte)-(Impfungen)*Impfwirksamkeit; %Die ANzahl der Empfängliche mit Impfstoff ergibt sich aus der Differenz der Gesamtbevölkerung, den bereits Infizierten und der Anzahl der 90% geimpften Peronen, die durch den Impfstoff geschützt sind
n=length(people); % gibt mir die Länge der Zeile innerhalb der Matrix an
times=[0:1:n-1];
%Grafikauusgabe
figure(666)
title ('Anzahl der Empfaenglichen')
plot (times, Empfaengliche./1000, 'g-', times,EmpfaenglicheMitImpfung./1000, 'b-', times, people./1000,'r-')
xlabel ('Tage ab dem 25. Februar')
ylabel ('Zahlen in Tausend')
legend ( "Empfaenglich ohne Impfungen" ,"Empfaenglich inkl. Impfung", "Gesamtbevoelkerung", "location", "west")
grid on
xticks([50,100,150,200,250,300,350,400,450,500])
axis([0 , n , 0 , 85000]
Tutoriumsaufgabe 4: Numerische Diskretisierung der Poissongleichung mit Finite-Differenzen-Methode (FDM)
[Bearbeiten](oder: Die Implementierung der Randwertaufgabe für homogene Dirichlet-Randbedingungen auf dem Rechteck)
Die Finite-Differenzen-Methode ist ein auf ein Gitter basierendes Verfahren, die die unbekannte Funktion auf endlich vielen Gitterpunkten
approximiert. Dabei wird der Differenzenquotient zur Annäherung der Ableitung der gesuchten Funktion genutzt.
Folglich wird mit Hilfe der Poissongleichung auf einem rechteckigem Gebiet und der Finiten Differenzen Methode die stationäre Diffusion implementiert.
Theoretische Grundlagen
[Bearbeiten]Die grundlegende Idee des Verfahren ist die Approximierung der Ortableitungen in den Differentialgleichungen an endlich vielen äquidistanten Gitterpunkten durch Differenzenquotienten. Die approximierten Lösungen der Differenzialgleichungen an den Gitterpunkten lassen sich dann durch das entsprechende Gleichungssystem berechnen. (Sprich: Das Prinzip des Verfahrens ist, dass die gesuchte Funktion u, die die Laplae-Gleichung und später auch die Reaktionsdiffusionsgleichung lösen sollte, nicht als Funktion gesucht wird, sondern in endlich vielen Punkten ausgewertet bzw. die Funktionswerte in endlich vielen Punkten, am sogenannten Gitter, gesucht werden.) Dabei werden die Ableitungen durch die Differenzenquotienten näherungsweise bestimmt und ersetzt. Hierfür ist das Taylorpolynom von Bedeutung: Die Differenzenquotienten ergeben sich aus der Taylorentwicklung (approximation der Ableitungen nach Abbruch der Taylorreihe) für den Punkt x+h um den Entwicklungspunkt x. .
Erster Differenzenquotient
[Bearbeiten](Approximierung der 1. Ableitung)
Sei f hinreichend oft differenzierbar, dann folgt:
- vorwärts Differenzenquotient : mit
- rückwärts Differenzenquotient : mit
- zentraler Differenzenquotient : mit
Zweiter Differenzenquotient
[Bearbeiten]Analog gilt zur Approximierung der 2. Ableitung:
Sei f hinreichend oft differenzierbar, dann folgt für aus der Differenz der ersten Differenzenquotienten mithilfe der Taylorentwicklung bis zur vierten Ableitung:
Die Güte der Approximation
[Bearbeiten]Allgemein bietet die Güte der Approximation ein Maß dafür, wie gut die Annäherung jeweils ist. Den jeweiligen Fehler der Differenzenquotienten kann man mit Hilfe des Landau-Symbols beschreiben:
Die Funktion bezeichnet dabei die Abschätzung nach oben. Da folgt daraus, je höher die Potenz beim , desto genauer ist die Annäherung. Ferner heißt es hier, dass der Fehler geringer ist als eine Kosntakte , die mit bzw multippliziert wird.
Randwertproblem
[Bearbeiten]Zunächst soll die Diffusion auf einem beschränkten Gebiet betrachtet werden.Hierfür ist es hilfreich, das Verhalten der Funktion auf dem Rand des Gebietes zu betrachten. Bei einer Randwertaufgabe sind diese durch Bedingungen festgelegt. In dieser Aufgabe wird die schon bekannte stationäre Poisson-Gleichung betrachtet. Insgesamt gibt es zwei Möglichkeiten, wie das Randwertproblem angegangen werden kann: als Dirichlet-Randwertproblem oder als Neumann Randwertproblem.
Dirichlet Randwerproblem
[Bearbeiten]Ist die gesuchte Funktion am Rand durch eine gegebene Funktion festgelegt , erfüllt die Dirichlet Randbedingung:
Neumann Randwerproblem
[Bearbeiten]Sind die Richtungsableitungen der Funktion in der Richtung des äußeren Normalenvektors gegeben,
erfüllt die Neumann Randbedingung:
Randwertprobleme auf einem Intervall (1D)
[Bearbeiten]Dirichlet Randwerproblem
[Bearbeiten]Sei . Gesucht werden Näherungen für die Funktionswerte auf dem äquidistanten, das heißt auf dem gleiche Abstände aufweisenden Gitter
G=
die Werte am Rand sind bekannt (Randbedingungen ).
Die zweiten Ableitungen der Funktionswerte werden mit dem zweiten Differenzenquotienten diskretisiert.
Damit ergibt sich das folgende lineare Gleichungsystem:
mit einer tridiagonaler Systemmatrix
und der rechten Seite des Systems , bei der die Anfangsbedingungen eingebaut sind.
Neumann Randwerproblem
[Bearbeiten]In diesem Fall sind die Ableitungen in die Normalenrichtungen :
gegeben. Um die Ableitungen in den Randpunkten zu approximieren, führen wir neue Unbekannte ein.
1. Möglichkeit: Approximation erster Ordnung
Für die Approximation der Ableitung an den Rändern gilt:,
- vorwärts Differenzenquotient
- rückwärts Differenzenquotient
Für die neuen Unbekannten die 0-te und die - te Gleichung angeben, gilt:
,
.
2. Möglichkeit: Approximation zweiter Ordnung
Um die Approximationsgüte der zweiten Differenzquotienten für die Approximation von im Inneren des Intervalls . Um die Randbedingungen zu erhalten wird der erste zentrale Differenzenquotient verwendet:
- .
Damit man das lineare Gleichungssystem nicht wieder um neue Gleichungen für ergänzen muss, eliminiert man diese Variablen mithilfe der Randbedingungen. Man erhält aus obigen Gleichungen für folgende Gleichungen für :
- ,
Ersetzt man in den Gleichungen für den zweiten Differenzenquotient aus obigen Gleichungen, erhält man
anstelle der ersten und letzter Gleichung des linearen Systems:
Die 2. Möglichkeit ist zwar genauer, doch wenn die Funktion eine Lösung des Neumannproblems ist, dann ist diese Lösung nicht eindeutig: Auch für jede beliebige Konstante ist eine Lösung. Existiert eine Lösung, dann muss diese folgende Integration erfüllen:
Randwertprobleme in 2 Raumdimensionen(2D)
[Bearbeiten]Dirichlet Randwerproblem
[Bearbeiten]Sei u die gesuchte Funktion definiert auf einem Rechteck D: . Nachfolgend betrachten wir die Poissongleichung mit den dirichlet-Randwertproblem mit homogenen Randbedingungen, wobei D das rechteckige Gebiet ist. Dann lauten die zweiten Differenzenquotienten , die die zweiten partiellen Ableitungen jeweils in den Richtungen x und y approximieren:
- ,
in jedem Gitterpunkt . Damit erhalten wir schließlich das Approximationsschema: Folglich werden die Randgitterpunkte wie folgt ersetzt:
- ,
Damit lässt sich ein lineares Gleichungssystem erstellen mit der Blocktridiagonalen Matrix :
mit Diagonalblock
und der Einheitsmatrix auf der Nebendiagonale.
Sollten die Randwerte der gesuchten Funktion unterschiedlich von Null sein, dann verändert sich die Matrix nicht. Stattdessen tauchen die Randwerte an den jeweiligen Stellen der rechten Seite auf (und zwar immer an der ersten und letzten Stelle in jedem Block auf).
Neumann Randwerproblem
[Bearbeiten]Bearbeitung der Aufgabenstellung
[Bearbeiten]Quelldichtefunktion f der rechten Seite der Poissongleichung
[Bearbeiten]In einem ersten Schritt wird die Quelldichtefunktion der rechten Seite der Poissongleichung, die die Flussgeschwindigkeit in das System (hier: die kontinuierlich hinzukommenden Neuinfizierungen) beschreibt, definiert.
%Definition Quelldichtefunktion function wert=Quellfunktion(x,y) if sqrt((x.-3.25).^2+(y.-3).^2)<=0.35 wert=1; else wert=0; endif endfunction
Dirichlet-Randproblem in 2D
[Bearbeiten]Das Gebiet D
[Bearbeiten]Das Gebiet wird durch die Endpunkte der Intervalle und die konstante Schrittweite durch die Anzahl der innteren -Punkte festgelegt. Infolgedessen sind die (inneren) Gitterpunkte folgendermaßen definiert:
(Die Anzahl der -Punkte ist anhand der festgelegten Gittergröße bestimmt, sodass die Punkte der oberen Reihe nicht aus austreten.)
Demnach ist das Gebiet D wie folgt definiert:
%definiere Endpunkte xend=8; yend=5.0; N=50
%definiere Schrittweite und M hx=xend/(N+1) hy=hx; M=floor((yend/hy))-1
%Koordinatenmatrix der Gitterpunkte [x,y]=meshgrid(hx:hx:xend-hx,hy:hy:yend-hy);
%konstanter Diffusionskoeffizient zur Beschreibung der Geschwindigkeit %(beschreibt die Verbreitungsgeschwindigkeit; je größer, desto schneller) a=1.0;
Inhomogene Randwertbedingungen
Sobald eine abhängige Variable auf dem Rand vorgegeben wird, liegt eine sogenannte Dirichlet Randbedingung vor. Als Dirichlet-Randbedingungen bezeichnet man die Werte, die auf dem jeweiligen Rand des Definitionsbereichs der Funktion angenommen werden sollen. Demnach wird bei einem Dirichlet Randwertproblem die gesuchte Funktion am Rand durch eine Funktion festgelegt.[17]
In unserem Fall soll nun diese Funktion für die verschiedenen Ränder einen konstanten Wert annehmen. Infolgedessen werden an den Randpunkten einfache Gleichungen generiert, die die Einhaltung der Randbedingungen sicherstellen:
%Dirichlet-Randbedingungen wert_unten=0.01; wert_oben=-0.01; wert_links=0.01; wert_rechts=0.01;
Im Anschluss daran wird die Systemmatrix generiert.
% Systemmatrix %------------------------------------------- Vec1=ones(N*M,1); %erzeugt Vektor aus Einsern der Laenge N*M
%Systemmatrix N^2xM^2 mit -4 auf der Diagonale und 1 auf den Nebendiagonalen und 1 auf den N und -N-ter Nebendiagonale. BB=diag(-4.*Vec1,0)+diag(ones(N*M-1,1),1)+ diag(ones(N*M-1,1),-1)+diag(ones(N*(M-1),1),N)+diag(ones(N*(M-1),1),-N); %Korrektur der Matrix (Blocktridiagonalitaet) for i=1:(M-1) BB(i*N+1,i*N)=0;BB(i*N,i*N+1)=0; endfor
% Matrix mit Diffkoeff/h^2 multiplizieren BB=BB*a/hx^2;

%Matrixdarstellung
figure (11);
%surface (BB);
spy (BB);
xlabel("Spalten")
ylabel("Zeilen")
zlabel("Matrix B")
title ("Systemmatrix B");
Nun muss noch die rechte Seite des Systems miteinbezogen werden.
%rechte Seite des Systems clear f; for i=1:N for j=1:M f(j,i)=1*Quellfunktion(x(j,i),y(j,i)); %Dirichlet Randbedingung unten und Oben: if j==1 f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+ (a/hx^2)*wert_unten; endif if j==M f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+(a/hx^2)*wert_oben; endif %Dirichlet Randbedingung links und rechts: if (i==1) f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+ (a/hx^2)*wert_links; endif if (i==N )f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+(a/hx^2)*wert_rechts; endif endfor endfor
Wichtig hierbei ist es die Ecken-Beiträge zu berücksichtigen, da dort jeweils der Differenzquotientient in x als auch in y Richtung (oben/unten) approximiert und aufaddiert werden muss.
f(1,1)=1*Quellfunktion(x(j,i),y(j,i))+(a/hx^2)*wert_links+(a/hx^2)*wert_unten; f(1,N)= 1*Quellfunktion(x(j,i),y(j,i))+(a/hx^2)*wert_rechts+(a/hx^2)*wert_unten; f(M,1)=1*Quellfunktion(x(j,i),y(j,i))+ (a/hx^2)*wert_links+(a/hx^2)*wert_oben; f(M,N)=1*Quellfunktion(x(j,i),y(j,i))+ (a/hx^2)*wert_rechts+ (a/hx^2)*wert_oben;
size (f) b=-1*reshape(f',N*M,1);
Nun wird das System gelöst.
% Lösung sol=BB\b; sol_matrix=reshape(sol,N,M);% Matrix mit N(Zeilen)x M(Spalten) sol_matrix=sol_matrix'; % Transponiert, wegen reshape %-------------------------------------------------

%Oeffne ein Bildfenster und plotte die Lösung auf dem realen Koordinatenfeld
%-------------------------------------------------
figure(2);
surfc(x,y,sol_matrix);
title ("Loesung");
ylabel("y")
xlabel("x")
colormap("hsv")
colorbar

%weiteres Bild mit Quellfunktion- rechte Seite des Systems
figure(3);
surfc(x,y,f);
title ("Quellfunktion");
ylabel("y")
xlabel("x")
%%colormap("hsv")
Gemischte Randbedingungen: Dirichlet- und Neumann-Randbedingungen
[Bearbeiten]In einem ersten Schritt wird erneut die Quellfunktion und das Gebiet festgelegt.
%Definition der Quellfunktion(vgl. a) function wert=Quellfunktion(x,y) if sqrt((x.-3.25).^2+(y.-3).^2)<=0.35 wert=1; else wert=0; endif endfunction
%definiere Gebiet D xend=8; yend=5.0; %Anzahl von X-Punkten, verkleinern Sie diese um die Struktur der Matrix in weiteren Zellen besser zu erkennen. N=50 hx=xend/(N+1) hy=hx; M=floor((yend/hy))-1
%Koordinatenmatrix der Gitterpunkte [x,y]=meshgrid(0:hx:xend,0:hy:yend); %Diffussionskoeffizient a=1.0;
Im Anschluss daran werden die Dirichlet-Randbedingungen beliebig festgelegt und die Neumann-Bedingungen implementiert. Für das Neumann-Randproblem muss das Gitter vergrößert werden. Die Systemmatrix wird dabei um neue Blockzeilen und -spalten erweitert.
% Dirichlet-Randbedingung wert_oben=0.1; wert_unten=0.1;
% Neumann Randbedingung (hier wird die Hilfestellung auf der wikiversity- Seite genutzt, vgl.https://de.wikiversity.org/wiki/Kurs:R%C3%A4umliche_Modellbildung/Aufgaben_Tutorium_kontinuerliche_r%C3%A4umliche_Modellierung#4._%C3%9Cbungsaufgabe_SW7:_Poissongleichung_mit_FDM) N=N+2; M=M+2; % Systemmatrix Vec1=ones(N*M,1); %erzeugt Vektor aus Einsern der Laenge N*M BB=diag(-4.*Vec1,0)+diag(ones(N*M-1,1),1)+ diag(ones(N*M-1,1),-1)+diag(ones(N*(M-1),1),N)+diag(ones(N*(M-1),1),-N);
%Korrektur der Matrix (Blocktridiagonalitaet) for i=1:(M-1) BB(i*N+1,i*N)=0;BB(i*N,i*N+1)=0; endfor
% Matrix mit Diffkoeff/h^2 multiplizieren BB=BB*a/hx^2; % Neumann RB für x: c* partial_x u=0 - einzelne Zeilen der Matrix ersetzen %---------------------------------------------------------------------- for i=1:(M-2) vector_up=zeros(1,N*M); vector_up(N*i+1)=a/hx; vector_up(N*i+2)=-a/hx; vector_down=zeros(1,N*M); vector_down(N*i+N)=a/hx; vector_down(N*i+N-1)=-a/hx; BB(i*N+1,:)=vector_up ; BB(i*N+N,:)=vector_down ; endfor

%Matrixdarstellung
figure (11);
%surface (BB);
spy (BB);
xlabel("Spalten")
ylabel("Zeilen")
zlabel("Matrix B")
title ("Systematrix B");
In einem nächsten Schritt muss erneut die rechte Seite angepasst werden.
%rechte Seite clear f; for i=1:N for j=1:M f(j,i)=1*Quellfunktion(x(j,i),y(j,i)); %Dirichlet Randbedingung unten und Oben: if j==1 f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+ (a/hx^2)*wert_unten; endif if j==M f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+(a/hx^2)*wert_oben; endif endfor endfor
In den Eckpunkten kommen Neumann- und Dirichlet-Randbedingungen zusammen, weshalb die Ecken angepasst werden müssen.
f(1,1)=1*Quellfunktion(x(j,i),y(j,i)); f(1,N)=1*Quellfunktion(x(j,i),y(j,i)); f(M,1)=1*Quellfunktion(x(j,i),y(j,i)); f(M,N)=1*Quellfunktion(x(j,i),y(j,i)); size(f); b=-1*reshape(f',N*M,1);
Danach wird das System gelöst.
sol=BB\b; sol_matrix=reshape(sol,N,M);% Matrix mit N(Zeilen)x M(Spalten) sol_matrix=sol_matrix'; % Transponiert, wegen reshape

%Oeffne ein Bildfenster und plotte die Lösung auf dem realen Koordinatenfeld
%-------------------------------------------------
figure(2);
surfc(x,y,sol_matrix);
title ("Loesung");
ylabel("y")
xlabel("x")
colormap("hsv")
colorbar

%weiteres Bild mit Quellfunktion- rechte Seite des Systems
figure(3);
surfc(x,y,f);
title ("Quellfunktion");
ylabel("y")
xlabel("x")
%%colormap("hsv")
Tutoriumsaufgabe 5: Epidemiologische Modellierung als Reaktionsdiffusionsprozess mit FDM
[Bearbeiten]Theoretische Grundlagen
[Bearbeiten]Die letzte Tutoriumsaufgabe beschäftigt sich mit der numerischen Diskretisierung der Reaktionsdiffusionsprozesses der Populationsdynamik. Das Prinzip ist simpel: Die inhomogene Reaktions-Diffusionsgleichung
wird in vier aufeinander folgenden Schritten diskretisiert bis daraus ein numerisch lösbares System von Differentialgleichungen erstellen werden kann.
Dabei beschreibt die unbekannte Funktion die Populationsdichte der (aktuellen order kummulierten) Infizierten, wobei der Reaktionsterm die zeitliche Dynamik der aktuellen oder Infizierten steuert. Somit stellt der Reaktionsterm den Zusammenhang zwischen dem räumlichen Infektionsverbreitung als Diffusionsprozess und dem dynamischen Kompartimentmodellen dar. Die Diskretisierung erfolgt in folgenden vier Schritten, die anschließend näher erläutert werden:
- Räumliche (Semi-)Diskretisierung der homogenen Diffusionsgleichung
- Räumliche (Semi-)Diskretisierung der Reaktionsdiffusionsgleichung
- Zeitdiskretisierung der Reaktion-Diffusionsgleichung
- Raumdiskretisierung des regionaldifferenzierten Diffusionskoffizienten
Räumliche (Semi-)Diskretisierung der homogenen Diffusionsgleichung
[Bearbeiten]Räumliche (Semi-)Diskretisierung der Reaktionsdiffusionsgleichung
[Bearbeiten]Zeitdiskretisierung der Reaktion-Diffusionsgleichung
[Bearbeiten]Raumdiskretisierung des regionaldifferenzierten Diffusionskoffizienten
[Bearbeiten]Diskrete Modellbildung
[Bearbeiten]In der diskreten Modellbildung unterscheiden wir zwischen der räumlichen und der zeitlichen Diskretisierung. Im Folgenden werden wir verschiedene Modelle betrachten, um epidemiologische Prozesse am Beispiel des Coronavirus diskret abzubilden. Wir betrachten also die räumliche und zeitliche Verbreitung des Coronavirus. Dies geschieht mit der Hilfe von Tabellenkalkulationsprogrammen. Unsere Wahl fiel hierzu auf die Microsoft-Software Excel.
Kontaktmodell
[Bearbeiten]Ähnlich zum deterministischen Kontaktmodell, das über Octave implementiert wurde, wollen wir die Virusverbreitung unter Individuen auf einem bestimmten Gebiet mittels Tabellenkalkulation (Excel) näher betrachten. Ein wesentlicher Unterschied soll hierbei jedoch die Tatsache sein, dass wir von einem Infizierten in einem geschlossenen Raum mit vier weiteren, nicht infizierten Personen ausgehen. Außerdem wollen wir eine überschaubare Zeitspanne betrachten (wir entscheiden uns für eine Minute).
Zunächst definieren wir uns ein Gebiet (wir haben uns zunächst für ein X-Gebiet entschieden). Auf diesem Raum wollen wir Personen zufällig bewegen lassen. Unter diesen ist genau eine infektiös. Diese lassen wir genau in der Mitte des Gebietes starten. Um die zufällige Bewegung der Individuen zu simulieren, vereinfachen wir die mögliche räumliche Positionierung, indem wir ein Schachbrettmuster "drüber legen": ausgehend von der alten Position des Individuums generieren wir zunächst die Zufallszahlen und , die wir entweder zur ursprünglichen Koordinate addieren oder davon subtrahieren. Dies hat den Vorteil, dass wir lediglich ganze Zahlen als - bzw- -Koordinate der Individuen betrachten, was zur besseren Veranschaulichkeit dient. Wenn die Koordinaten am Rand des Gebiets (d.h. oder ) liegen, soll die nächste Koordinate wiederum im Gebiet liegen. Dies erhalten wir, indem wir die Randwerte als Sonderfall betrachten: wenn eine Koordinate den Wert erhält, soll die darauffolgende Koordinate entweder oder sein. Wir dürfen also nur oder addieren. Analog gilt zum Fall, dass die Koordinate den Wert erhält, dass diese im nächsten Schritt entweder bleibt oder den Wert erhält. Dies gelingt mit dem folgenden Befehl:
=IF(B3=0;B3+RANDBETWEEN(0;1);IF(B3=$U$3;B3-RANDBETWEEN(0;1);B3+RANDBETWEEN(-1;1)))
bzw.
=IF(C3=0;C3+RANDBETWEEN(0;1);IF(C3=$U$4;C3-RANDBETWEEN(0;1);C3+RANDBETWEEN(-1;1)))
Dieses Generieren einer neuen Position hat den Vorteil, dass die Personen in einem Zeitschritt ∆ sich maximal eine Längeneinheit in - bzw. -Richtung bewegen können. Ausgehend von der Längeneinheit Meter () und Zeiteinheit Sekunden () bewegen sich die Personen also maximal .
Die Startposition restlichen Personen (Person , , und ) lassen wir zufällig generieren, was mit dem Befehl geschieht. Sie erhalten das obige Bewegungsmuster. Personen bis sollen nicht infektiös sein, d.h. sie sind potentielle Virusträger und können von Person infiziert werden. Eine Infektion kann erst stattfinden, wenn sich die infektiöse Person ausreichend nahe einer empfänglichen Person - befindet. Dazu betrachten wir den Abstand der beiden Personen: Wenn beide x- und y-Koordinaten einer nicht infizierten Person näher als einen Infektionsabstand (hier zunächst ) an die Koordinaten der infizierten Person herankommen, also und , so soll zunächst ein Zufallsexperiment durchgeführt werden. (Anmerkung: Die Indizes stehen hierbei für die Indikation der Person - natürlich müssen die Koordinaten zum selben Zeitpunkt betrachtet werden.) Der Befehl generiert eine Zufallszahl zwischen und . Wenn der Abstand der Koordinaten größer als ist, so soll die Zelle mit "-" gefüllt werden:
=IF(AND(ABS(B3-D3)<U$6$; ABS(C3-E3)<U$6$); RAND(); "-")
Um den Status der Person im Zeitpunkt zu bestimmen (also anzuzeigen, ob die Person infiziert oder nicht infiziert wurde), müssen wir außerdem eine Formatierung durchnehmen: Dazu betrachten wir die Zelle der generierten Zufallszahl. Wenn diese Zufallszahl kleiner als eine Infektionswahrscheinlichkeit (hier zunächst ) ist, so kommt es zur Infektion - der Status der Person wird mit "INF" bezeichnet. Andernfalls ist die nicht infizierte Person der Infektion zunächst "entkommen" und bleibt weiterhin empfänglich - ihr Status wird mit "SUS" bezeichnet:
=IF(F3<$U$8; "INF"; "SUS")
Um den Wechsel von "nicht infiziert" zu "infiziert" zu verhindern, muss der Befehl ab dem Zeitpunkt erweitert werden: zunächst wird mittels einer ersten IF-Bedingung abgefragt werden, ob die Person zu einem früheren Zeitpunkt bereits als infiziert galt. Falls dies der Fall ist, soll auch diese Zelle zum Zeitpunkt mit "INF" gekennzeichnet sein. Falls dies nicht der Fall ist, soll der alte Befehl (s.o.) zum Tragen kommen. Dies erfüllt der folgende Befehl:
=IF(G3="INF";"INF"; IF(F4<$U$8;"INF"; "SUS"))
Es ist zu erkennen, dass früher oder später alle fünf Personen im Raum infiziert sind und die Infektionen von Person 1 hervorgerufen wurden. Anhand der Zellen der stattfindenden Zufallsexperimente erkennen wir, dass es durchaus öfter zur Unterschreitung des Abstandes kam, allerdings meist ohne die Folgen einer Infektion.
Im Folgenden wollen wir einige Parameter ändern und das veränderte Infektionsgeschehen betrachten. Dazu variieren wir die Starposition des Infizierten, die Größe des Gebiets, den Infektionsradius und die Infektionswahrscheinlichkeit.
Veränderte Startposition
[Bearbeiten]Veränderte Größe des Gebiets
[Bearbeiten]Zunächst betrachten wir ein größeres Gebiet als das Ursprüngliche. Dazu verdoppeln wir die Länge und Breite des Gebietes auf x. Dementsprechend vervierfacht sich die Fläche des betrachteten Gebietes. Daher erwarten wir, dass es zu weniger Begegnungen und Infektionen kommt.
Wir erkennen, dass es zu weniger Begegnungen des Infizierten mit anderen Personen kommt und auch nur eine einzige Infektion stattfindet.
Weiterhin wollen wir ein kleineres Gebiet betrachten. Dazu wählen wir ein x-Gebiet. Wir erwarten, dass am Ende des betrachteten Zeitintervalls alle vier Personen von Person 1 infiziert worden sind.
Tatsächlich lässt sich beobachten, dass es vermehrt zum Kontakten mit dem Infizierten sowie Infektion jeder Person kommt - und das nach nicht einmal .
Veränderung des Infektionsradius
[Bearbeiten]Wir betrachten zunächst die Vergrößerung des Infektionsradius: von auf . Wir erwarten mehr bzw. frühere Infektionen.
Tatsächlich werden vier von fünf Personen infiziert. Insgesamt kommt es zu deutlich mehr Begegnungen, bei denen sich die Personen infizieren können.
Nun betrachten wir einen verkleinerten Infektionsradius: von auf . Wir erwarten weniger Infektionen.
Tatsächlich kommt es zu lediglich zwei Infektionen.
Veränderung der Infektionswahrscheinlichkeit
[Bearbeiten]Wir betrachten einen vergrößerte Infektionswahrscheinlichkeit: statt . Wir erwarten mehr Infektionen.
Entgegen unserer Annahme kam es nicht unbedingt zu mehr Infektionen. Die Zahl der Infektionen unterschreitet sogar die im Vergleich zur Infektionswahrscheinlichkeit . Weitere Durchläufe bestätigen: eine größere Infektionswahrscheinlichkeit sorgt nicht automatisch für mehr Infektionen. Eine Infektion kann nur stattfinden, wenn sich die Personen ausreichend nah beieinander befinden. Erst dann kommt die Infektionswahrscheinlichkeit zum Tragen: sie erhöht das Risiko einer Person, infiziert zu werden.
Schließlich wollen wir noch die maximale Infektionswahrscheinlichkeit von betrachten. Das bedeutet, dass es bei einer Begegnung zwangsläufig zur Infektion kommt. Wir erwarten, dass alle infiziert werden.
Tatsächlich kommt es zu vielen Begegnungen und Infektionen. Da diese zwangsläufig zu einer Infektion führen, infizieren sich alle.
Vor- und Nachteile
[Bearbeiten]Vorteile
- Überblick über Status der Personen
- Überprüfen von Auswirkungen innerhalb eines geschlossenen Raumes
- realistische Gehgeschwindigkeit bei Zeiteinheit Sekunden und Längeneinheit Meter (ca. )
- Modell zur (Rück-)Verfolgung von Infektionen, die ein einziger Infizierter verursacht: insofern realitätsnah, als dass ein gerade frisch Infizierter nicht binnen Sekunden einen weiteren Menschen ansteckt
Nachteile
- Infektionen unter frisch Infizierten nicht betrachtet
- Wechseln von Infizierten zu Empfänglichen (Genesung) muss außer Acht gelassen werden
- keine räumliches Plotten (Tabellenkalkulation)
- Befehle werden sehr lang und unübersichtlich wenn Fehler entstehen bzw. andere Szenarien betrachtet werden sollen
SIR-Modell zur Corona-Verbreitung via Excel
[Bearbeiten]In vorangegangenen Abschnitten haben wir gesehen, wie das SIR-Modell funktioniert. Dieses wollen wir nun für die Modellierung der Verbreitung des Coronavirus heranziehen. Dazu betrachten wir Deutschland im Zeitraum von zwei Jahren (Januar 2020 bis Januar 2022). Das Startdatum soll der 1. Januar 2020 sein. Knapp vier Wochen nach dem Startdatum (genauer: am 27. Januar 2020) kam es zum ersten Corona-Fall in Deutschland. [18][19] Wir runden die Bevölkerungsanzahl Deutschlands auf 83,24 Millionen Einwohner.[20] Außerdem gehen wir von einer Infektionszeitspanne von 14 Tagen aus. Im folgenden wollen wir nun die Ausbreitung des Coronavirus mit verschiedenen Basisreproduktionszahlen (R0) modellieren.
Das Robert-Koch-Institut (RKI) definiert die Basisreproduktionszahl als Angabe, "wie viele Personen von einer infizierten Person durchschnittlich angesteckt werden, vorausgesetzt, dass in der Bevölkerung keine Immunität besteht und keine infektionspräventiven Maßnahmen ergriffen wurden. Eine Infektion breitet sich langfristig nur dann aus, wenn ihr R0 über 1 liegt. Für die Basisreproduktionszahl des ursprünglichen SARS-CoV-2 „Wildtyps“ wurde in mehreren systematischen Reviews (48-50) ein mittlerer Wert (Median) von 2,8 bis 3,8 ermittelt. Neue Virusvarianten können eine höhere Übertragbarkeit und dementsprechend höhere Basisreproduktionszahl aufweisen".[21] Weiterhin wird darauf hingewiesen, dass es in Studien zu Pandemiebeginn "zu einer Überschätzung des Wertes gekommen sein [kann], da sich die Infektion zu Beginn meist v.a. unter Personen ausbreitet, die überdurchschnittlich viele Kontakte haben und sich möglicherweise auch besonders sorglos und ungeschützt begegnet sind" (ebd.). Es ist wichtig, darauf hinzuweisen, dass die Basisreproduktionszahl eine "Größe [ist], die für eine bestimmte Bevölkerung zu einem bestimmten Zeitpunkt spezifisch ist, es kann somit kein allgemeingültiger Wert angegeben werden. Sie kann verstanden werden als das Produkt aus der durchschnittlichen Zahl der Kontakte mit anderen Personen pro Zeiteinheit, der Übertragungswahrscheinlichkeit und der Dauer der Infektiosität" (ebd.).
Beobachtung und Evaluation
[Bearbeiten]Es ist deutlich zu erkennen, dass bei einer höheren Basisreproduktionszahl die Anzahl der Infektionen steigt. Die Kurve der Infizierten (rot) wird also höher und zugleich steiler und verschiebt sich weiter nach links, d.h. der Peak der Infektionen findet früher statt. Dies scheint auch nicht verwunderlich: je mehr Leute sich infizieren, desto schneller ist die Bevölkerung durchseucht.
Weiterhin ist erkennbar, dass mit steigender Basisreproduktionszahl die Anzahl der Empfänglichen (gelb) schneller abnimmt. Bei einer niedrigeren Basisreproduktionszahl (z.B. R0=1,8) bleibt die Anzahl der Empfänglichen nach dem Abklingen der Infektionen beinahe konstant bei ca. 18.000.000, wohingegen sie bei einer höheren Basisreproduktionszahl (z.B. R0=2,5) auf einem beständigen niedrigen Niveau von ca. 2.000.000 bleibt.
Die Anzahl der Genesenen (grün) verhält sich "umgekehrt" zur Anzahl der Empfänglichen: Bei höherer Basisreproduktionszahl (z.B. R0=2,5) flacht die Kurve auf einem deutlich höheren Niveau (ca. 81.000.000) ab als bei einer niedrigeren Basisreproduktionszahl (ca. 66.000.000 bei R0=1,8).
Weiterhin ist erkennbar, dass das SIR-Modell bei höheren Basisreproduktionszahlen (R0=3 bzw. R0=3,3) an seine Grenzen stößt. Hier übersteigt die Anzahl der Genesenen die Zahl der Gesamtbevölkerung. Die Anzahl der Empfänglichen und die Anzahl der Infizierten werden sogar für kurze Zeit negativ. Beide Phänomene sind per definitionem nicht realitätsnah. Außerdem berücksichtigt dieses SIR-Modell weder infektionspräventiven Maßnahmen, wie etwa Kontaktbeschränkungen oder Impfungen, noch das Durchmischen von Bevölkerungsgruppen, bspw. hervorgerufen durch den internationalen Flugverkehr.
Zum Vergleich der Auswirkungen einer veränderten Bevölkerungszahl soll nachfolgend von der Gesamtbevölkerung der Erde ausgegangen werden (etwa 7,8 Milliarden Menschen im Mai 2020).[22]
Hier lassen sich die gleichen Phänomene beobachten, die zuvor bei dem von der deutschen Gesamtbevölkerung ausgehenden SIR-Modell.
Optimierung: Anpassen der Infektionszahlen über Basisreproduktionszahl
[Bearbeiten]Im folgenden wollen wir das SIR-Modell so anpassen, dass es grob das Infektionsgeschehen der andauernden Coronavirus-Pandemie abbildet (siehe nachfolgende Grafik).[23] Wir haben uns auf die Zahl der Infizierten beschränkt, da diese die über den gesamten Verlauf der Corona-Pandemie am häufigsten aufgetretene Zahl ist. Außerdem erleichtert uns diese Reduktion die Darstellung der Daten im Diagramm, da wir mit einem genaueren Maßstab arbeiten können.
Hierzu betrachten wir infektionspräventive Maßnahmen, die sich in das bestehende Modell einbauen lassen. Wir beschränken uns auf die Berücksichtigung der folgenden Eckdaten:
- 22.03.2020: Erster Lockdown in Deutschland mit Kontaktverboten, Schließung von Einzelhandel, Restaurants, Friseuren sowie Aussetzen des Präsenzunterrichts an Schulen
- 12.12.2020: Bund und Länder beschließen einen harten Lockdown, der am 16.12. in Kraft tritt
- 21.04.2021: Bundesnotbremse, u.a. mit Ausgangssperren
- Juni 2021: Die Delta-Variante breitet sich in Deutschland aus.
Diese wollen wir in das SIR-Modell einbauen, indem wir die Auswirkungen der Maßnahmen anhand der Abänderung der Basisreproduktionszahl abschätzen. Da die Wirkung der Maßnahmen frühestens zwei Wochen nach ihrer Einführung beobachtet werden können, betrachten wir die folgenden Eckdaten:
Die Historie der Fallzahlen liefert uns folgende Eckdaten:[24]
- 08.04.2020: 111.779 Infizierte
- 23.09.2020: 278.172 Infizierte
- 30.12.2020: 1.723.696 Infizierte
- 10.03.2021: 2.533.206 Infizierte
- 05.05.2021: 3.473.409 Infizierte
- 22.09.2021: 4.173.627 Infizierte
- 19.11.2021: 5.267.885 Infizierte
Durch Ausprobieren und Anpassen der Werte auf den zwischen den Eckdaten liegedenden Zeiträume erhalten wir die folgenden Basisreproduktionszahlen (inkl. Interpretation):
- 01.01.2020 bis 08.04.2020: R0=9,2 - exponentielle Verbreitung des Virus ohne jedwede Einschränkungen
- 08.04.2020 bis 23.09.2020: R0=0,628 - Abklingen der Fallzahlen
- 23.09.2020 bis 30.12.2020: R0=2,87 - erneute ungehinderte Virusverbreitung
- 30.12.2020 bis 10.03.2021: R0=0,8 - Abklingen der Fallzahlen
- 10.03.2021 bis 05.05.2021: R0=1,31 - vermehrte Ausbreitung des Virus
- 05.05.2021 bis 22.09.2021: R0=0,55 Abklingen der Fallzahlen
- 22.09.2021 bis 12.01.2021: R0=4,7 - vermehrte Ausbreitung des Virus
Weiterhin wollen wir das modifizierte SIR-Modell betrachten und die Zahl der Verstorbenen einbeziehen.
Transportmodell
[Bearbeiten]Im Folgenden wollen wir die Virusverbreitung zwischen verschiedenen Standorten genauer untersuchen. Dies geschieht in zwei Schritten:
- Transportprozess: Austausch von Personen zwischen Standorten
- Epidemiologischer Prozess: Virusverbreitung an den jeweiligen Standorten
Transportprozess
[Bearbeiten]Dazu betrachten wir die vier deutschen Millionenstädte Berlin, Hamburg, München und Köln. Diese sollen als Knotenpunkte dienen: Aufgrund ihrer geographischen Lage können diese stellvertretend für ihre umliegendenden Metropolregionen bzw. Bundesländer betrachtet werden. Wir möchten uns jedoch zunächst auf die Einwohnerzahlen der vier Städte beschränken.
Wir möchten zunächst die Transportprozesse zwischen diesen vier Knotenpunkten betrachten, was uns das nachfolgende Schema liefert. Die Knotenpunkte sind untereinander verknüpft. Die Doppelpfeile indizieren jeweils zwei Richtungen, in denen Transportprozesse stattfinden. Die Zahlen an den Pfeilenden stellt den relativen Anteil dar, die sich in Richtung dieses Pfeiles bewegen. Beispielsweise bedeutet die Zahl 0,2 an dem Ende des Pfeils, der von Berlin nach Hamburg zeigt, dass 20% der Einwohner bzw. Menschen, die sich gerade in Berlin aufhalten, nach sich nach Hamburg bewegen. Die Pfeile, die von einem Knotenpunkt auf denselben zeigt, indiziert den Anteil der Personen, die an diesem Knotenpunkten stationiert bleiben, diese Stadt also nicht verlassen. Die Anteile wurde aufgrund der geographischen Lage und Verbundenheit der Städte untereinander geschätzt und sollen lediglich als Richtwerte dienen. Beispielsweise ist der Austausch zwischen Berlin und Hamburg recht hoch, da diese Städte in der Realität eine etwa weite Autofahrt bzw. eine etwa zweieinhalbstündige ICE-Fahrt voneinander trennt. Im Gegensatz dazu trennt Berlin und München etwa bzw. fünfeinhalb Stunden ICE-Fahrt.
Zunächst fassen wir die Transportprozesse zwischen den Knotenpunkten mathematisch auf. Hier kommen Matrizen ins Spiel. Wir beziffern die Städte mit ihren jeweiligen Anfangsbuchstaben (H für Hamburg, B für Berlin, M für München und K für Köln) und fassen die Transportprozesse in einer 4x4-Matrix auf. Dies liefert uns die folgende Transportmatrix.
Die Transportmatrix wird nun "von oben nach links gelesen". Um den Transportprozess zwischen zwei Städten zu erkennen, betrachtet man also die Spalte des Ausgangsortes und die Zeile des Zielortes. Hierbei ist zu beachten, dass die Spaltensummen der Transportmatrix immer gleich dem Wert sin. Weiterhin fassen wir die Einwohnerzahlen der Städte als einen Spaltenvektor auf. Diesen ordnen wir dem anfänglichen Zeitwert zu. Mithilfe des Befehls , der die Matrizenmultiplikation durchführt, können wir nun unseren Anfangsvektor mit der Transportmatrix multiplizieren. Wir erhalten einen neuen Spaltenvektor, der uns die Einwohnerzahlen zum neuen Zeitpunkt angibt. Dieses Prozedere können wir nun fortführen, um zukünftige Einwohnerzahlen zu bestimmten Zeitpunkten zu bestimmen.
Epidemiologischer Prozess
[Bearbeiten]Im nächsten Schritt wollen wir den epidemiologischen Prozess der Virusverbreitung mit einbeziehen. Hierzu nutzen wir das SIR-Modell. Wir unterteilen die Personen an den jeweiligen Knotenpunkten in drei Gruppen: Susceptible (S), Infected (I) und Recovered (R).
Wir treffen die folgenden Annahmen:
- 70 % der empfänglichen Personen sollen weiterhin empfänglich bleiben, d.h. sie infizieren sich nicht mit dem Virus
- 30 % der Empfänglichen wechseln zur Gruppe der Infizierten, d.h. die infizieren sich mit dem Virus
- 50 % der Infizierten bleiben weiterhin infiziert
- 50 % der Infizierten wechseln zur Gruppe der Genesenen
- 100 % der Genesenen bleiben in dieser Gruppe, d.h. sie sind gegen das Virus immun
Diese haben wir im folgenden Schema veranschaulicht:
Das Schema fassen wir in einer 3x3-Matrix auf, die wir nennen. Dabei gilt es zu beachten, dass die Zeilensummen der Infektionsmatrix stets gleich dem Wert betragen muss.
Im Gegensatz zur wir die "von links nach oben gelesen". Um beispielsweise zu ermitteln, wie hoch der Anteil der Personen ist, die genesen sind und in die Gruppe der Infizierten wechseln, betrachtet man die Zeile der Genesenen (R) und die Spalte der Infizierten (I). Ein Eintrag mit dem Wert bedeutet, dass es zu keinem Austausch der beiden Gruppen in dieser Richtung gibt. Umgekehrt bedeutet der Wert , dass alle Personen in die jeweilige Gruppe wechseln.
Zum Anfangswert soll lediglich ein/e Infizierte/r im Knotenpunkt München sein, da dies die Region ist, in der der erste Corona-Fall ("Patient Null") in Deutschland auftrat.[25] Da zu Beginn noch niemand in Deutschland bzw. den Knotenpunkten Kontakt mit dem Virus hatte, sind alle restlichen Einwohner ihrer jeweiligen Gruppe der Empfänglichen zuzuordnen. Demnach gibt es zum Startwert auch noch keine Genesenen Personen. Die Ausgangssituation beschreibt die folgende Abbildung ( zum Zeitpunkt ):
Im folgenden wird zusätzlich zum Transportprozess die Virusinfektion mit einbezogen. Dazu wird erneut der Befehl verwendet, um die mit der zu multiplizieren. Die daraus resultierende Matrix gibt uns das Infektionsgeschehen an den Knotenpunkten aus. Diese wird wiederum unter Nutzung des Befehls mit der multipliziert, um die SIR-Lage zum neuen Zeitpunkt zu beschreiben. Anschließend kommt es wieder zum Infektionsgeschehen an den jeweiligen Knotenpunkten usw.
Plot
[Bearbeiten]Ausgehend von den obigen Parametern wollen wir das bisherige Modell nun grafisch ausgeben lassen, um die Zusammenhänge anschaulicher zu gestalten. Dazu nutzen wir die Excel-interne Plot-Funktion.
Es ist zu erkennen, dass die Zahl der Empfänglichen (S) schnell abnimmt. Durch den regen Austausch der Standorte untereinander verteilen sich Infizierte schnell. Da es zu keinen Einschränkungen kommt, befindet sich die Zahl der Infizierten auf einem hohen Niveau. Diese wechseln nach und nach zu den Genesenen (R), die sich der Einwohnerzahl der jeweiligen Standorte annähert. Da sich die Infizierten rasant ausbreiten und es sehr schnell zu Infektionen kommt, wollen wir die Ansteckungen ein wenig eindämmen. Im Folgenden wird das Modell mit einer Infektion von o,1 gefüttert:
Es ist eine deutlich langsamere Verbreitung erkennbar: die Empfänglichen lehmigen weniger schnell ab und die Genesenen nehmen weniger schnell zu. Das kommt von weniger Infektionen an den Standorten.
Ergänzungen Octave-Tutorial
[Bearbeiten]Diese Ergänzungen wurden bei dem Octave-Tutorial vorgenommen, um die Implementation der Gruppe bzgl. der verwendeten Octave-Befehle nachvollziehbar zu machen.
- Matrix-Multiplikation in Octave - notwendig für die Modellierung diskreter Transportprozesse.
Skripte in Octave
[Bearbeiten]Referenzieren Sie hier die von Ihnen verwendeten Skripte und Bibliotheken in Octave[26] oder R/Studio
Quellenangaben
[Bearbeiten]Notieren Sie hier die von Ihnen verwendete Literatur
- Boto von Querenburg (2013) Mengentheoretische Topologie - Springer-Lehrbuch
- Wikipedia-Artikel zu Epidemiologie (2020)[27]
- Seite „Finite-Differenzen-Methode“. In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 12. April 2021, 14:06 UTC. URL: https://de.wikipedia.org/w/index.php?title=Finite-Differenzen-Methode&oldid=210858579 (Abgerufen: 23. Juni 2021, 14:09 UTC)
Literatur
[Bearbeiten]- ↑ Coronaviridae Study Group of the International Committee on Taxonomy of, V. (2020). The species Severe acute respiratory syndrome-related coronavirus: classifying 2019-nCoV and naming it SARS-CoV-2. Nat Microbiol 5, 536-544.
- ↑ Health - United Nations Sustainable Development. In: United Nations Sustainable Development. (Online [abgerufen am 18. März 2018]).
- ↑ Climate Change - United Nations Sustainable Development. In: United Nations Sustainable Development. (Online [abgerufen am 18. März 2018]).
- ↑ Global Partnerships - United Nations Sustainable Development. In: United Nations Sustainable Development. (Online [abgerufen am 18. März 2018]).
- ↑ ZEIT ONLINE, 27. Oktober 2021 / DIE ZEIT Nr.44/2021, 28. Oktober 2021 https://www.zeit.de/2021/44/ursprung-coronavirus-labor-unfall-wuhan-debatte-pandemie
- ↑ ZEIT ONLINE, 10. November 2021 / DIE ZEIT Nr.46/2021, 11. November 2021 https://www.zeit.de/2021/46/christian-drosten-coronavirus-virologie-pandemie-wissenschaft-impfung
- ↑ https://www.oemg.ac.at/DK/LFT_Vortraege/2017/Folien_PauerStampfer.pdf
- ↑ https://www.oemg.ac.at/DK/LFT_Vortraege/2017/Folien_PauerStampfer.pdf (Folie 5)
- ↑ https://www.uni-siegen.de/fb6/src/mueller/berichte/extrakte_nr5.pdf
- ↑ Lawrence C. Evans: Partial Differential Equations. American Mathematical Society, Providence RI 1998, ISBN 0-8218-0772-2 (Graduate studies in mathematics 19)
- ↑ vgl. https://netmath.vcrp.de/downloads/Skripte/Hundertmark/ExpRegressionSeite/exponentielle_regression.html , insbesondere den Punkt Berechnung
- ↑ vergleich der Kurve mit Daten aus folgender Auflistung: https://www.gew-bw.de/aktuelles/detailseite/corona-rueckblick-2020/
- ↑ https://de.wikipedia.org/wiki/COVID-19-Pandemie_in_Deutschland
- ↑ vgl.: https://de.wikipedia.org/wiki/COVID-19-Pandemie_in_Deutschland
- ↑ https://de.wikipedia.org/wiki/COVID-19-Impfung_in_Deutschland#Impfstatistik
- ↑ https://impfdashboard.de/
- ↑ vgl. https://de.wikipedia.org/wiki/Dirichlet-Randbedingung
- ↑ Tagesschau, 28. Januar 2020.
- ↑ Süddeutsche Zeitung, 28. März 2020, https://www.sueddeutsche.de/bayern/coronavirus-bayern-ausbruch-rueckblick-1.4794769
- ↑ Weltbank, 2021, https://data.worldbank.org/indicator/SP.POP.TOTL?locations=DE
- ↑ RKI, 14. Juli 2021 https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Steckbrief.html;jsessionid=F3DDD2E2CD4006D0250FDA9AAEDEB210.internet091?nn=13490888#doc13776792bodyText4
- ↑ Countrymeters, 14. Mai 2020, https://countrymeters.info/de/World
- ↑ Bundesregierung bzw. Robert-Koch-Institut https://www.bundesregierung.de/breg-de/aktuelles/fallzahlen-coronavirus-1738210
- ↑ Berliner Morgenpost, 17. November 2021, https://interaktiv.morgenpost.de/corona-virus-karte-infektionen-deutschland-weltweit/
- ↑ Spiegel Online, 16. Mai 2020, https://www.spiegel.de/wissenschaft/medizin/erster-corona-fall-in-deutschland-die-unglueckliche-reise-von-patientin-0-a-2096d364-dcd8-4ec8-98ca-7a8ca1d63524
- ↑ Silva, I., & Moody, G. B. (2014). An open-source toolbox for analysing and processing physionet databases in matlab and octave. Journal of open research software, 2(1).
- ↑ „Epidemiologie“. In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 25. Juni 2020, 09:27 UTC. URL: https://de.wikipedia.org/w/index.php?title=Epidemiologie&oldid=201288758 (Abgerufen: 25. Juni 2020, 10:24 UTC)






















































![{\displaystyle x\in [0,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d35e3fa30fa9d0e9f57923fb0101848d4fea625a)



![{\displaystyle [x,x+\Delta x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3adcf4c82ed495a6478a43316b80154c95a040f5)









![{\displaystyle (5)([c(x)u'(x)])'=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4d45bf020ce06aa59711cc28333382eb3fc4166)











![{\displaystyle \partial _{t}u(x,t)-\partial _{x}(c(x)\partial _{x}u(x,t))=f(x,t),\ x\in [0,L]\subset \mathbb {R} \ \quad {\mbox{oder}}\quad \partial _{t}u(x,t)-div\ (c(x)\nabla u(x,t))=f(x,t),\ x\in \ \mathbb {R} ^{n},\ t\in \mathbb {R} ^{+}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b7d31a21c11d68430958208a765e1a760f66c42)












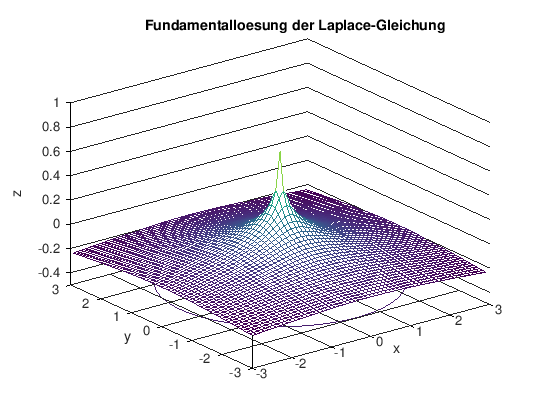


















































































![{\displaystyle {\vec {y}}'=f({\vec {y}},t),\quad t\in [t_{0},T],\ {\vec {y}}(t)=(y_{1}(t),y_{2}(t),y_{3}(t))^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/298cd7c7fe3f7d7da77fe04f9974038b04818e90)


































![{\displaystyle x\in [a,b]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/773c4531c022eddb88d782c0a6ccd2bae7fc18fa)
![{\displaystyle \{x_{i}=a+ih,\ i=1,\ldots ,n\in \mathbb {N} \}\subset [a,b],\quad h={\frac {b-a}{n+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab4c3721e88eb097b68924849616c30ce086c07c)


























![{\displaystyle u:\mathbb {R} ^{2}\to \mathbb {R} ,\ {\bf {x}}=(x,y)\in D:=[a,b]\times [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a87d21f93bf0f4dbb957b71fc78c2be7aa60735)















































































