Die nachfolgenden ZV werden hier kurz vorgestellt. Selbstverständlich können auch für die Parameter dieser Verteilungen Punkt- und Intervallschätzungen vorgenommen werden, es soll hier jedoch nicht weiter darauf eingegangen werden.
Die Zufallsvariable  heißt Poisson-verteilt mit der durch Beobachtung zu erwartenden Ereignishäufigkeit
heißt Poisson-verteilt mit der durch Beobachtung zu erwartenden Ereignishäufigkeit  , wenn ihre Wahrscheinlichkeitsfunktion gegeben ist durch
, wenn ihre Wahrscheinlichkeitsfunktion gegeben ist durch

für  .
.
Die Poissonverteilung gibt die Wahrscheinlichkeit für die Anzahl von Ereignissen an, die unabhängig voneinander in einem räumlichen Gebiet oder zeitlichen Intervall auftreten. Ist  Poisson-verteilt mit Parameter
Poisson-verteilt mit Parameter  , so gilt
, so gilt

und

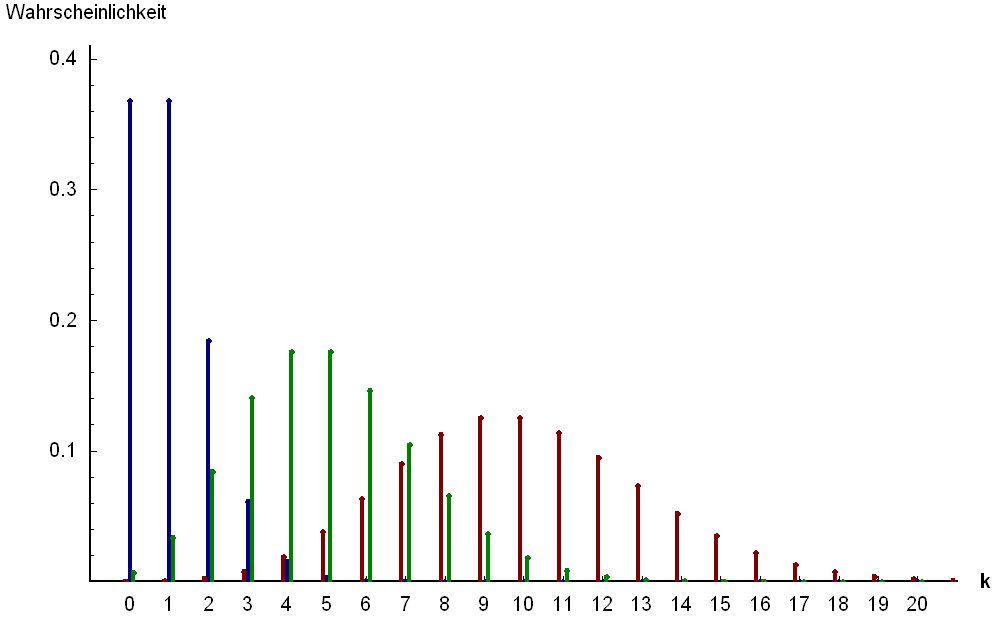
Mit  (blau),
(blau),  (grün) und
(grün) und  (rot).
(rot).
Für die Poissonverteilung gilt die Rekursionsformel

für  und es gilt
und es gilt  .
.
Es folgt wie zuvor für

und für
 .
.
Da bei der Poissonverteilung jedoch theoretisch gesehen unendlich viele Ereignisse in dem betrachteten Intervall auftreten können, wird die kumulierte Verteilung für  mittels einer unendlichen Summe dargestellt:
mittels einer unendlichen Summe dargestellt: 
Dennoch gilt die Normierbarkeit, da die Wahrschienlichkeiten für  abnehmen und sich beliebig nahe an die
abnehmen und sich beliebig nahe an die  annähern. Somit liegt zwar eine unendliche Summe vor, diese konvergiert jedoch, d.h. hat einen endlichen Wert, nämlich
annähern. Somit liegt zwar eine unendliche Summe vor, diese konvergiert jedoch, d.h. hat einen endlichen Wert, nämlich

An einer radioaktiven Probe aus Uran werden pro Sekunde im Mittel  Zerfälle gemessen. Die Zufallsvariable
Zerfälle gemessen. Die Zufallsvariable  , welche die Anzahl der Zerfälle pro Sekunde angibt, ist somit Poissonverteilt und es ergibt sich die folgende Wahrscheinlichkeitsverteilung:
, welche die Anzahl der Zerfälle pro Sekunde angibt, ist somit Poissonverteilt und es ergibt sich die folgende Wahrscheinlichkeitsverteilung:

Daraus resultieren die folgenden Wahrscheinlichkeiten für  :
:




Kommentar:  , andere Zerfälle sind auch möglich, aber die Wahrscheinlichkeiten sind so gering, dass sie nicht weiter aufgeführt werden.
, andere Zerfälle sind auch möglich, aber die Wahrscheinlichkeiten sind so gering, dass sie nicht weiter aufgeführt werden.

Die Poissonverteilung stellt den Grenzwert für eine binomialverteilte ZV mit unendlich vielen Versuchen dar.
Gegeben sei eine Poissonverteilte ZV  mit
mit  . Bestimmen Sie Erwartungswert, Varianz und die folgenden Wahrscheinlichkeiten:
. Bestimmen Sie Erwartungswert, Varianz und die folgenden Wahrscheinlichkeiten:
-

-

-

-

-

Zufallsexperimente mit geometrisch verteilten ZV können als Spezialfälle binomialverteilter ZV betrachtet werden, wobei hier zwischen zwei Varianten unterschieden wird:
- Durchführen eines binomialverteilten Zufallsexperiemnt, bis ein "Treffer "
erzielt wird und die ZV  gibt die Anzahl der Versuche an.
gibt die Anzahl der Versuche an.
- Durchführen eines binomailverteilten Zufallsexperiment, bis ein "Treffer"erzielt wird und die ZV
 gibt die Anzahl der Fehlversuche an.
gibt die Anzahl der Fehlversuche an.
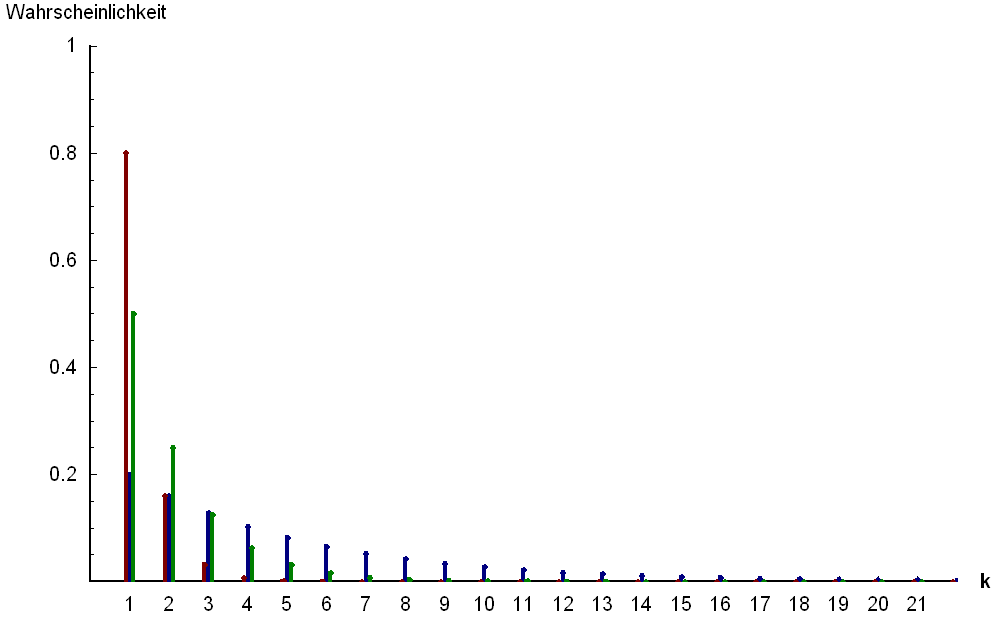
Zu Fall 1 (Anzahl der Versuche) mit  (blau),
(blau),  (grün) und
(grün) und  (rot).
(rot).
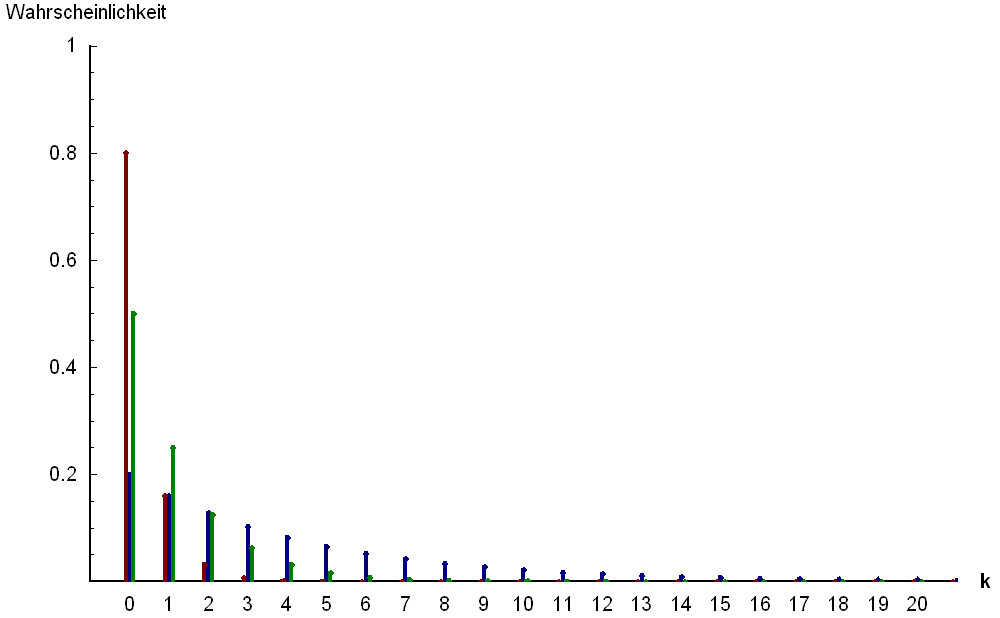
Zu Fall 2 (Anzahl der Fehlversuche) mit  (blau),
(blau),  (grün) und
(grün) und  (rot).
(rot).
Die beiden Varianten stehen in der Beziehung  .
.
Somit ergeben sich die beiden folgenden Formeln für die Bestimmung der Wahrscheinlichkeit:
Bestimmung der Wahrscheinlichkeiten für X
[Bearbeiten]Für die ZV  gilt:
gilt:





Bestimmung der Wahrscheinlichkeiten für Y
[Bearbeiten]Für die ZV  gilt:
gilt:





Werfen einer Münze bis zum Eintreten von Kopf.





In R wird die zweite Varainte betrachtet, welche die Anzahl der Fehlversuche zählt, https://stat.ethz.ch/R-manual/R-devel/library/stats/html/Geometric.html
Gegeben Sei die geometrisch verteilte ZV  mit
mit  . Bestimmen Sie Erwartungswert, Varianz und die folgenden Wahrscheinlichkeiten (Variante 2):
. Bestimmen Sie Erwartungswert, Varianz und die folgenden Wahrscheinlichkeiten (Variante 2):
-

-

-

-

-

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.






























































