Die Finite Differenzen Methode ist neben dem Finite Volumen Verfahren und dem Finite Elementen Verfahren eine der bekanntesten numerischen Diskretisierungsverfahren für partielle Differentialgleichungen.
u
(
x
,
t
)
{\displaystyle u(x,t)}
P
i
,
j
=
(
x
i
,
y
j
)
,
i
=
1
,
…
N
x
,
j
=
1
,
…
N
y
{\displaystyle P_{i,j}=(x_{i},y_{j}),\ i=1,\ldots N_{x},\ j=1,\ldots N_{y}}
In FDM werden die Ableitungen der gesuchten Funktion durch
Differenzenquotienten ersetzt.
Approximation von ln(x) durch Taylorpolynome der Grade 1, 2, 3 bzw. 10 um die Entwicklungsstelle 1. Die Polynome konvergieren nur im Intervall (0, 2]. Der Konvergenzradius ist also 1. Author: Georg Johann Die Taylorentwicklung der Funktion
f
:
R
→
R
{\displaystyle f:\mathbb {R} \to \mathbb {R} }
x
+
h
{\displaystyle x+h}
x
{\displaystyle x}
f
(
x
+
h
)
=
∑
k
=
0
∞
f
(
k
)
(
x
)
k
!
(
h
)
k
=
f
(
x
)
+
f
′
(
x
)
.
h
+
f
″
(
x
)
h
2
2
!
+
f
‴
(
x
)
.
h
3
3
!
+
…
{\displaystyle f(x+h)=\sum _{k=0}^{\infty }{\frac {f^{(k)}(x)}{k!}}(h)^{k}=f(x)+f'(x).h+f''(x){\frac {h^{2}}{2!}}+f'''(x).{\frac {h^{3}}{3!}}+\ldots }
Die Differenzenquotienten ergeben sich als Approximation der Ableitungen von
f
{\displaystyle f}
Sei Funktion
f
{\displaystyle f}
Lagrangeschem Restglied
f
(
x
+
h
)
=
f
(
x
)
+
h
f
′
(
x
)
+
f
″
(
x
)
h
2
2
+
f
‴
(
θ
)
h
3
3
!
{\displaystyle {\begin{array}{rcl}f(x+h)&=&f(x)+hf'(x)+f''(x){\frac {h^{2}}{2}}+f'''(\theta ){\frac {h^{3}}{3!}}\end{array}}}
mit
θ
∈
(
x
,
x
+
h
)
{\displaystyle \theta \in (x,x+h)}
für den ersten (vorwärts-) Differenzenquotient
D
h
+
f
(
x
)
:=
f
(
x
+
h
)
−
f
(
x
)
h
=
f
′
(
x
)
+
f
″
(
x
)
h
2
+
f
‴
(
θ
1
)
h
2
6
,
θ
1
∈
(
x
,
x
+
h
)
{\displaystyle D_{h}^{+}f(x):={\frac {f(x+h)-f(x)}{h}}=f'(x)+f''(x){\frac {h}{2}}+f'''(\theta _{1}){\frac {h^{2}}{6}},\ \ \theta _{1}\in (x,x+h)}
für den ersten (rückwärts-) Differenzenquotient mit Anwendung von
−
h
{\displaystyle -h}
h
{\displaystyle h}
D
h
−
f
(
x
)
:=
f
(
x
)
−
f
(
x
−
h
)
h
=
f
′
(
x
)
−
f
″
(
x
)
h
2
+
f
‴
(
θ
2
)
h
2
6
,
θ
2
∈
(
x
−
h
,
x
)
{\displaystyle D_{h}^{-}f(x):={\frac {f(x)-f(x-h)}{h}}=f'(x)-f''(x){\frac {h}{2}}+f'''(\theta _{2}){\frac {h^{2}}{6}},\ \ \theta _{2}\in (x-h,x)}
für den ersten zentralen Differenzenquotient durch aus der Summe
1
2
(
D
+
f
(
x
)
+
D
−
f
(
x
)
)
{\displaystyle {\frac {1}{2}}{\big (}D^{+}f(x)+D^{-}f(x){\big )}}
D
h
f
(
x
)
:=
f
(
x
+
h
)
−
f
(
x
−
h
)
2
h
=
f
′
(
x
)
+
(
f
‴
(
θ
1
)
+
f
‴
(
θ
2
)
)
h
2
12
,
θ
1
,
θ
2
∈
(
x
,
x
±
h
)
{\displaystyle D_{h}f(x):={\frac {f(x+h)-f(x-h)}{2h}}=f'(x)+(f'''(\theta _{1})+f'''(\theta _{2})){\frac {h^{2}}{12}},\ \ \theta _{1},\theta _{2}\in (x,x\pm h)}
Alle drei erste Differenzenquotienten approximieren die erste Ableitung:
D
h
±
f
(
x
)
,
D
h
f
(
x
)
≈
f
′
(
x
)
{\displaystyle D_{h}^{\pm }f(x),D_{h}f(x)\approx f'(x)}
h
→
0
{\displaystyle h\to 0}
f
{\displaystyle f}
[
a
,
b
]
{\displaystyle [a,b]}
x
,
x
±
h
∈
[
a
,
b
]
{\displaystyle x,\ x\pm h\in [a,b]}
Lemma 1:
Ist
f
∈
C
2
[
a
,
b
]
{\displaystyle f\in C^{2}[a,b]}
x
∈
[
h
,
b
−
h
]
{\displaystyle x\in [h,b-h]}
|
D
h
±
f
(
x
)
−
f
′
(
x
)
|
≤
h
2
C
1
{\displaystyle |D_{h}^{\pm }f(x)-f'(x)|\leq {\frac {h}{2}}C_{1}}
C
1
:=
max
x
∈
[
a
,
b
]
|
f
″
(
x
)
|
{\displaystyle C_{1}:=\max _{x\in [a,b]}|f''(x)|}
f
∈
C
3
[
a
,
b
]
{\displaystyle f\in C^{3}[a,b]}
x
∈
[
h
,
b
−
h
]
{\displaystyle x\in [h,b-h]}
|
D
h
f
(
x
)
−
f
′
(
x
)
|
≤
h
2
6
C
2
{\displaystyle |D_{h}f(x)-f'(x)|\leq {\frac {h^{2}}{6}}C_{2}}
C
2
=
max
x
∈
[
a
,
b
]
|
f
‴
(
x
)
|
{\displaystyle C_{2}=\max _{x\in [a,b]}|f'''(x)|}
Beweis: Aus den Gleichungen für
erste Differenzenquotienten
◻
{\displaystyle \ \square }
D
2
f
(
x
)
≈
f
″
(
x
)
{\displaystyle D^{2}f(x)\approx f''(x)}
x
{\displaystyle x}
f
{\displaystyle f}
Die Formel für
D
2
f
(
x
)
{\displaystyle D^{2}f(x)}
D
h
+
f
(
x
)
−
D
h
−
f
(
x
)
{\displaystyle D_{h}^{+}f(x)-D_{h}^{-}f(x)}
D
h
2
f
(
x
)
:=
f
(
x
+
h
)
−
2
f
(
x
)
+
f
(
x
−
h
)
h
2
=
f
″
(
x
)
+
(
f
(
I
V
)
(
θ
1
)
+
f
(
I
V
)
(
θ
2
)
)
h
2
4
!
.
{\displaystyle D_{h}^{2}f(x):={\frac {f(x+h)-2f(x)+f(x-h)}{h^{2}}}=f''(x)+{\big (}f^{(IV)}(\theta _{1})+f^{(IV)}(\theta _{2}){\big )}{\frac {h^{2}}{4!}}.}
Die Formel für den zweiten Differenzenquotient
D
h
2
f
(
x
)
{\displaystyle D_{h}^{2}f(x)}
D
h
/
2
f
(
x
)
{\displaystyle D_{h/2}f(x)}
D
h
/
2
(
D
h
/
2
f
(
x
)
)
=
D
h
/
2
(
f
(
x
+
h
/
2
)
−
f
(
x
−
h
/
2
)
h
)
=
1
h
(
f
(
x
+
h
)
−
f
(
x
)
h
−
f
(
x
)
−
f
(
x
−
h
)
h
)
≡
D
h
2
f
(
x
)
{\displaystyle D_{h/2}{\big (}D_{h/2}f(x){\big )}=D_{h/2}{\Big (}{\frac {f(x+h/2)-f(x-h/2)}{h}}{\Big )}={\frac {1}{h}}{\Big (}{\frac {f(x+h)-f(x)}{h}}-{\frac {f(x)-f(x-h)}{h}}{\Big )}\equiv D_{h}^{2}f(x)}
Lemma 2:
Ist
f
∈
C
4
[
a
,
b
]
{\displaystyle f\in C^{4}[a,b]}
x
∈
[
h
,
b
−
h
]
{\displaystyle x\in [h,b-h]}
|
D
h
2
f
(
x
)
−
f
″
(
x
)
|
≤
h
2
12
C
3
{\displaystyle |D_{h}^{2}f(x)-f''(x)|\leq {\frac {h^{2}}{12}}C_{3}}
C
3
:=
max
x
∈
[
a
,
b
]
|
f
(
I
V
)
(
x
)
|
{\displaystyle C_{3}:=\max _{x\in [a,b]}|f^{(IV)}(x)|}
Beweis: Aus der Gleichung für
zweiten Differenzenquotient .
Der Term
(
f
(
I
V
)
(
θ
1
)
+
f
(
I
V
)
(
θ
2
)
)
h
2
24
{\displaystyle {\Big (}f^{(IV)}(\theta _{1})+f^{(IV)}(\theta _{2}){\Big )}{\frac {h^{2}}{24}}}
D
h
2
f
(
x
)
{\displaystyle D_{h}^{2}f(x)}
◻
{\displaystyle \ \square }
Die Fehler der Differenzenquotienten kann man mithilfe des Landau-Symbols beschreiben:
D
h
f
(
x
)
=
f
′
(
x
)
+
O
(
h
2
)
{\displaystyle D_{h}f(x)=f'(x)+{\cal {O(h^{2})}}}
D
h
±
f
(
x
)
=
f
′
(
x
)
+
O
(
h
)
{\displaystyle D_{h}^{\pm }f(x)=f'(x)+{\cal {O(h)}}}
D
h
2
f
(
x
)
=
f
″
(
x
)
+
O
(
h
2
)
{\displaystyle D_{h}^{2}f(x)=f''(x)+{\cal {O(h^{2})}}}
Für die Approximation Ableitungen höherer Ordnung siehe Höhere Differenzenquotienten .
D
⊂
R
n
{\displaystyle D\subset {\mathbb {R} }^{n}}
∂
D
{\displaystyle \partial D}
−
Δ
u
(
x
)
=
f
(
x
)
.
{\displaystyle -\Delta u(x)=f(x).}
Ist die gesuchte Funktion
u
{\displaystyle u}
∂
D
{\displaystyle \partial D}
g
{\displaystyle g}
u
{\displaystyle u}
Dirichlet Randbedingung :
−
Δ
u
(
x
)
=
f
(
x
)
x
∈
D
{\displaystyle \displaystyle -\Delta u(x)=f(x)\qquad x\in D}
u
(
x
)
=
g
(
x
)
x
∈
∂
D
.
{\displaystyle \displaystyle \quad u(x)=g(x)\quad \ \ x\in \partial D.}
Richtungsableitung (L.Sittinger, S.Schmitz) Sind die Richtungsableitungen der Funktion
u
{\displaystyle u}
u
{\displaystyle u}
Neumann Randbedingung :
−
Δ
u
(
x
)
=
f
(
x
)
x
∈
D
{\displaystyle -\Delta u(x)=f(x)\quad x\in D}
∂
u
(
x
)
∂
n
→
≡
∇
u
⋅
n
→
=
g
(
x
)
x
∈
∂
D
.
{\displaystyle {\frac {\partial u(x)}{\partial {\vec {n}}}}\equiv \nabla u\cdot {\vec {n}}=g(x)\quad x\in \partial D.}
Numerische Diskretisierung des Randwertproblems [ Bearbeiten ]
Dirichletproblem auf dem Intervall (1D) [ Bearbeiten ] Sei
x
∈
[
a
,
b
]
⊂
R
{\displaystyle x\in [a,b]\subset \mathbb {R} }
[
a
,
b
]
{\displaystyle [a,b]}
{
x
i
=
a
+
i
h
,
i
=
1
,
…
,
n
∈
N
}
⊂
[
a
,
b
]
,
h
=
b
−
a
n
+
1
{\displaystyle \{x_{i}=a+ih,\ i=1,\ldots ,n\in \mathbb {N} \}\subset [a,b],\quad h={\frac {b-a}{n+1}}}
die Werte
u
(
a
)
,
u
(
b
)
{\displaystyle u(a),u(b)}
Diskretisierung durch Differenzenquotient [ Bearbeiten ] In diesem Fall handelt es sich um gewöhnliche Differentialgleichung. Die zweiten Ableitungen werden mit Hilfe des zweiten Differenzenquotienten diskretisiert:
D
h
2
u
(
x
i
)
=
u
i
+
1
−
2
u
i
+
u
i
−
1
h
2
≈
u
″
(
x
i
)
{\displaystyle D_{h}^{2}u(x_{i})={\frac {u_{i+1}-2u_{i}+u_{i-1}}{h^{2}}}\approx u''(x_{i})}
i
=
1
,
…
n
{\displaystyle i=1,\ldots n}
u
i
:=
u
(
x
i
)
{\displaystyle u_{i}:=u(x_{i})}
Nach der Anwendung der obigen Formel für jedes
i
=
1
,
…
n
{\displaystyle i=1,\ldots n}
u
0
=
u
(
a
)
,
u
n
+
1
=
u
(
b
)
{\displaystyle u_{0}=u(a),\ u_{n+1}=u(b)}
D
h
2
u
(
x
1
)
,
D
h
2
u
(
x
n
)
{\displaystyle D_{h}^{2}u(x_{1}),\ D_{h}^{2}u(x_{n})}
u
→
h
:=
(
u
1
,
…
u
n
)
T
{\displaystyle {\vec {u}}_{h}:=(u_{1},\ldots u_{n})^{T}}
A
h
u
→
h
=
f
→
h
,
{\displaystyle A_{h}{\vec {u}}_{h}={\vec {f}}_{h},}
A
h
{\displaystyle A_{h}}
f
→
h
{\displaystyle {\vec {f}}_{h}}
A
h
=
−
1
h
2
.
(
−
2
1
0
…
0
1
−
2
1
⋮
⋮
⋱
⋱
⋱
0
…
1
−
2
)
,
(
f
1
+
u
0
h
2
f
2
⋮
f
n
−
1
f
n
+
u
n
+
1
h
2
.
)
{\displaystyle A_{h}={\frac {-1}{h^{2}}}.{\begin{pmatrix}-2&1&0&\ldots &0\\1&-2&1&&\vdots \\\vdots &\ddots &\ddots &\ddots &\\0&&\ldots &1&-2\end{pmatrix}},\qquad {\begin{pmatrix}f_{1}+{\frac {u_{0}}{h^{2}}}\\f_{2}\\\vdots \\f_{n-1}\\f_{n}+{\frac {u_{n+1}}{h^{2}}}.\end{pmatrix}}}
siehe
dieses Beispiel .
[ Bearbeiten ] Die Systemmatrix
A
h
,
h
>
0
{\displaystyle A_{h},h>0}
positiv definit.
Der Lösungsvektor (numerische Lösung)
u
→
h
{\displaystyle {\vec {u}}_{h}}
Übersicht der Lösungsverfahren für lineare Gleichungssysteme.
SW7: Neumannproblem auf dem Intervall (1D) [ Bearbeiten ] Gegeben seien die Randbedingungen für die Ableitungen in den Normalrichtungen
−
1
,
1
{\displaystyle -1,1}
−
u
′
(
a
)
=
α
,
u
′
(
b
)
=
β
.
{\displaystyle -u'(a)=\alpha ,\ u'(b)=\beta .}
Um die Ableitungen in den Randpunkten zu approximieren, führen wir neue Unbekannte
u
0
:=
u
(
a
)
,
u
n
+
1
:=
u
(
b
)
{\displaystyle u_{0}:=u(a),\ u_{n+1}:=u(b)}
Verwendet man einseitige Differenzenquotienen für die Approximation der Ableitung an den Rändern,
den vorwärts -Differenzenquotient
D
h
+
u
(
a
)
=
u
1
−
u
0
h
=
u
′
(
a
)
+
O
(
h
)
{\displaystyle D_{h}^{+}u(a)={\frac {u_{1}-u_{0}}{h}}=u'(a)+{\mathcal {O}}(h)}
den rückwärts -Differenzenquotient
D
h
−
u
(
b
)
=
u
n
+
1
−
u
n
h
=
u
′
(
b
)
+
O
(
h
)
{\displaystyle D_{h}^{-}u(b)={\frac {u_{n+1}-u_{n}}{h}}=u'(b)+{\mathcal {O}}(h)}
erhält man für die neuen Unbekannte
u
0
,
u
n
+
1
{\displaystyle u_{0},\ u_{n+1}}
n
+
1
{\displaystyle {n+1}}
u
0
=
u
1
+
h
α
+
O
(
h
2
)
{\displaystyle u_{0}=u_{1}+h\alpha +{\mathcal {O}}(h^{2})}
u
n
+
1
=
u
n
+
h
β
+
O
(
h
2
)
{\displaystyle u_{n+1}=u_{n}+h\beta +{\mathcal {O}}(h^{2})}
Aufgabe Stellen Sie die Systemmatrix
A
~
h
{\displaystyle {\tilde {A}}_{h}}
O
(
h
)
{\displaystyle {\mathcal {O}}(h)}
Um die Approximationsgüte der zweiten Differenzquotienten für die Approximation von
u
″
(
x
)
{\displaystyle u''(x)}
O
(
h
2
)
{\displaystyle {\mathcal {O}}(h^{2})}
ersten zentralen Differenzenquotient :
D
h
u
(
a
)
=
u
1
−
u
−
1
2
h
=
u
′
(
a
)
+
O
(
h
2
)
{\displaystyle D_{h}u(a)={\frac {u_{1}-u_{-1}}{2h}}=u'(a)+{\mathcal {O}}(h^{2})}
D
h
u
(
b
)
=
u
n
+
2
−
u
n
2
h
=
u
′
(
b
)
+
O
(
h
2
)
{\displaystyle D_{h}u(b)={\frac {u_{n+2}-u_{n}}{2h}}=u'(b)+{\mathcal {O}}(h^{2})}
Damit man das lineare Gleichungssystem nicht wieder um neue Gleichungen für
u
−
1
,
u
n
+
2
{\displaystyle u_{-1},\ u_{n+2}}
D
h
{\displaystyle D_{h}}
u
−
1
,
u
n
+
2
{\displaystyle u_{-1},\ u_{n+2}}
u
−
1
=
u
(
a
−
h
)
=
u
1
−
2
h
u
′
(
a
)
+
O
(
h
3
)
=
u
1
+
2
h
α
+
O
(
h
3
)
{\displaystyle u_{-1}=u(a-h)=u_{1}-2hu'(a)+{\mathcal {O}}(h^{3})=u_{1}+2h\alpha +{\mathcal {O}}(h^{3})}
u
n
+
2
=
u
(
b
+
h
)
=
u
n
+
2
h
u
′
(
b
)
+
O
(
h
3
)
=
u
n
+
2
h
β
+
O
(
h
3
)
{\displaystyle u_{n+2}=u(b+h)=u_{n}+2hu'(b)+{\mathcal {O}}(h^{3})=u_{n}+2h\beta +{\mathcal {O}}(h^{3})}
Ersetzt man
u
−
1
,
u
n
+
2
{\displaystyle u_{-1},\ u_{n+2}}
D
h
2
u
(
x
0
)
,
D
h
2
u
(
x
n
+
1
)
{\displaystyle D_{h}^{2}u(x_{0}),\ D_{h}^{2}u(x_{n+1})}
2
u
1
−
2
u
0
h
2
=
−
2
α
/
h
+
O
(
h
)
,
2
u
n
−
2
u
n
+
1
h
2
=
−
2
β
/
h
+
O
(
h
)
.
{\displaystyle {\frac {2u_{1}-2u_{0}}{h^{2}}}=-2\alpha /h+{\mathcal {O}}(h),\quad {\frac {2u_{n}-2u_{n+1}}{h^{2}}}=-2\beta /h+{\mathcal {O}}(h).}
Bemerkung : Dass die ersten zwei Gleichungen die Approximation mit einem Fehler insgesamt von der Größenordnung
O
(
h
2
)
{\displaystyle {\mathcal {O}}(h^{2})}
h
/
2
{\displaystyle {h}/{2}}
Aufgabe : Stellen Sie die Systemmatrix
A
~
h
{\displaystyle {\tilde {A}}_{h}}
[ Bearbeiten ]
A
~
h
∈
R
(
n
+
2
)
×
(
n
+
2
)
{\displaystyle {\tilde {A}}_{h}\in \mathbb {R} ^{(n+2)\times (n+2)}}
A
~
h
1
=
0
{\displaystyle {\tilde {A}}_{h}{\bf {1}}={\bf {0}}}
1
=
(
1
,
1
,
…
,
1
)
,
0
=
(
0
,
0
,
…
,
0
)
.
{\displaystyle {\bf {1}}=(1,1,\ldots ,1),\ {\bf {0}}=(0,0,\ldots ,0).}
Man kann zeigen (Gauß Eliminierung)
R
a
n
g
(
A
~
h
)
=
n
+
1
,
{\displaystyle Rang({\tilde {A}}_{h})=n+1,\ }
Damit ist die Lösung dieses linearen System nicht eindeutig.
[ Bearbeiten ] Wenn die Funktion
u
(
x
)
{\displaystyle u(x)}
u
(
x
)
+
c
{\displaystyle u(x)+c}
Die Ableitungen am Rand bestimmen die Steigung der gesuchten Funktion, aber nicht deren Wert. Durch das Festlegen eines Wertes der gesuchten Funktion, z.B.
u
0
=
u
(
a
)
{\displaystyle u_{0}=u(a)}
∫
a
b
u
″
(
x
)
d
x
=
u
′
(
b
)
−
u
′
(
a
)
=
α
+
β
=
∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}u''(x)dx=u'(b)-u'(a)=\alpha +\beta =\int _{a}^{b}f(x)dx}
siehe
):
∫
D
Δ
u
(
x
)
d
x
=
∫
∂
D
∇
u
⋅
n
→
d
S
x
=
∫
∂
D
g
d
S
x
=
∫
d
f
(
x
)
d
x
{\displaystyle \int _{D}\Delta u(x)dx=\int _{\partial D}\nabla u\cdot {\vec {n}}dSx=\int _{\partial D}gdSx=\int _{d}f(x)dx}
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
g
{\displaystyle g}
f
{\displaystyle f}
Im stationären Zustand balanciert der Materialfluss durch die Ränder die Materialquelle im Inneren .
u
:
R
2
→
R
,
x
=
(
x
,
y
)
∈
D
:=
[
a
,
b
]
×
[
c
,
d
]
{\displaystyle u:\mathbb {R} ^{2}\to \mathbb {R} ,\ {\bf {x}}=(x,y)\in D:=[a,b]\times [c,d]}
Dirichlet-Randwertproblem mit homogenen Randbedingungen:
−
Δ
u
(
x
)
=
f
(
x
)
in
D
⊂
R
2
,
u
=
0
auf
∂
D
{\displaystyle {\begin{aligned}-\Delta u(x)&=f(x)\ \ {\mbox{in }}\ D\subset \mathbb {R} ^{2},\\u&=0\ \ \ \ \ \ \ \ {\mbox{auf}}\ \ \partial D\end{aligned}}}
Der einfachste Fall ist die Verwendung eines äquidistanten Gitters
{
(
x
i
,
y
j
)
,
i
=
1
,
…
n
,
j
=
1
,
…
m
}
{\displaystyle \{(x_{i},y_{j}),\ i=1,\ldots n,\,j=1,\ldots m\}}
h
=
x
i
−
x
i
−
1
=
y
j
−
y
j
−
1
=
b
−
a
n
+
1
=
d
−
c
m
+
1
,
i
=
1
,
…
n
,
j
=
1
,
…
m
{\displaystyle h=x_{i}-x_{i-1}=y_{j}-y_{j-1}={\frac {b-a}{n+1}}={\frac {d-c}{m+1}},\ i=1,\ldots n,\,j=1,\ldots m}
Man bezeichne die Approximationen der Lösung in den Gitterpunkten
(
x
i
,
y
j
)
:
{\displaystyle (x_{i},y_{j}):}
u
i
,
j
:≈
u
(
x
i
,
y
j
)
,
i
=
1
,
…
n
,
j
=
1
,
…
m
.
{\displaystyle u_{i,j}:\approx u(x_{i},y_{j}),\ i=1,\ldots n,\ j=1,\ldots m.}
Die zweiten Differenzenquotienten
D
h
,
x
2
u
(
x
i
,
y
j
)
,
D
h
,
y
2
u
(
x
i
,
y
j
)
{\displaystyle D_{h,x}^{2}u(x_{i},y_{j}),\ D_{h,y}^{2}u(x_{i},y_{j})}
∂
2
u
(
x
i
,
y
j
)
∂
x
2
≈
D
h
,
x
2
u
(
x
i
,
y
j
)
:=
u
(
x
i
+
1
,
y
j
)
−
2
u
(
x
i
,
y
j
)
+
u
(
x
i
−
1
,
y
j
)
h
2
=
u
i
+
1
,
j
−
2
u
i
,
j
+
u
i
−
1
,
j
h
2
{\displaystyle {\frac {\partial ^{2}u(x_{i},y_{j})}{\partial x^{2}}}\approx D_{h,x}^{2}u(x_{i},y_{j}):={\frac {u(x_{i+1},y_{j})-2u(x_{i},y_{j})+u(x_{i-1},y_{j})}{h^{2}}}={\frac {u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{h^{2}}}}
∂
2
u
(
x
i
,
y
j
)
∂
y
2
≈
D
h
,
y
2
u
(
x
i
,
y
j
)
:=
u
(
x
i
,
y
j
+
1
)
−
2
u
(
x
i
,
y
j
)
+
u
(
x
i
,
y
j
−
1
)
h
2
=
u
i
,
j
+
1
−
2
u
i
,
j
+
u
i
,
j
−
1
h
2
{\displaystyle {\frac {\partial ^{2}u(x_{i},y_{j})}{\partial y^{2}}}\approx D_{h,y}^{2}u(x_{i},y_{j}):={\frac {u(x_{i},y_{j+1})-2u(x_{i},y_{j})+u(x_{i},y_{j-1})}{h^{2}}}={\frac {u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{h^{2}}}}
(
x
i
,
y
j
)
{\displaystyle (x_{i},y_{j})}
Wir erhalten schließlich das Approximationsschema:
Δ
u
(
x
i
,
y
j
)
≈
u
i
+
1
,
j
+
u
i
,
j
+
1
−
4
u
i
,
j
+
u
i
−
1
,
j
+
u
i
,
j
−
1
h
2
,
i
=
1
,
…
n
,
j
=
1
,
…
m
.
{\displaystyle \Delta u(x_{i},y_{j})\approx {\frac {u_{i+1,j}+u_{i,j+1}-4u_{i,j}+u_{i-1,j}+u_{i,j-1}}{h^{2}}},\qquad i=1,\ldots n,\ j=1,\ldots m.}
In den Randgitterpunkten
(
x
0
,
⋅
)
,
(
x
n
+
1
,
⋅
)
,
(
⋅
,
y
0
)
,
(
⋅
,
y
m
+
1
)
{\displaystyle (x_{0},\cdot ),\ (x_{n+1},\cdot ),\ (\cdot ,y_{0}),\ (\cdot ,y_{m+1})}
u
{\displaystyle u}
u
(
x
0
,
y
j
)
=
u
(
x
n
+
1
,
y
j
)
=
0
,
j
=
1
,
…
m
{\displaystyle u(x_{0},y_{j})=u(x_{n+1},y_{j})=0,\ j=1,\ldots m}
u
(
x
i
,
y
0
)
=
u
(
x
i
,
y
m
+
1
)
=
0
,
i
=
1
,
…
n
{\displaystyle u(x_{i},y_{0})=u(x_{i},y_{m+1})=0,\ i=1,\ldots n}
Die unbekannten Approximationen der Lösung in den Gitterpunkten
(
x
i
,
y
j
)
,
u
i
,
j
≈
u
(
x
i
,
y
j
)
,
i
=
1
,
…
n
,
j
=
1
,
…
m
,
{\displaystyle (x_{i},y_{j}),\ u_{i,j}\approx u(x_{i},y_{j}),\ i=1,\ldots n,\ j=1,\ldots m,}
Beispiel:
y
1
{\displaystyle y_{1}}
x
1
→
x
n
{\displaystyle x_{1}\to x_{n}}
Die Approximationswerte
u
i
,
j
{\displaystyle u_{i,j}}
u
→
h
{\displaystyle {\vec {u}}_{h}}
u
→
h
=
(
u
1
,
1
,
u
2
,
1
,
…
u
n
,
1
|
…
|
u
1
,
m
,
…
u
n
,
m
)
T
.
{\displaystyle {\vec {u}}_{h}=(u_{1,1},u_{2,1},\ldots u_{n,1}|\ldots |u_{1,m},\ldots u_{n,m})^{T}.}
In der selben Reihenfolge wird auch der Vektor der rechten Seite aufgestellt,
f
→
h
=
(
f
1
,
1
,
f
2
,
1
,
…
f
n
,
1
|
…
|
f
1
,
m
,
…
f
n
,
m
)
T
,
f
i
,
j
:=
f
(
x
i
,
y
j
)
.
{\displaystyle {\vec {f}}_{h}=(f_{1,1},f_{2,1},\ldots f_{n,1}|\ldots |f_{1,m},\ldots f_{n,m})^{T},\ f_{i,j}:=f(x_{i},y_{j}).}
Nach der oben beschriebener numerischen Diskretisierung und Assemblierung des unbekannten Vektors ergibt sich ein lineares Gleichungssystem
A
h
u
→
h
=
f
→
h
{\displaystyle A_{h}{\vec {u}}_{h}={\vec {f}}_{h}}
Blocktridiagonaler Matrix
A
h
∈
R
n
.
m
×
n
.
m
{\displaystyle A_{h}\in {\mathbb {R} }^{n.m\times n.m}}
A
h
=
−
1
h
2
(
B
I
…
0
I
B
I
⋮
⋮
⋱
⋱
⋱
0
…
I
B
)
{\displaystyle A_{h}={\frac {-1}{h^{2}}}{\begin{pmatrix}B&I&&\ldots &0\\I&B&I&&\vdots \\\vdots &\ddots &\ddots &\ddots &\\0&&\ldots &I&B\end{pmatrix}}}
B
=
(
−
4
1
0
…
0
1
−
4
1
…
0
⋮
⋱
⋱
⋱
1
0
…
0
1
−
4
)
,
B
∈
R
n
×
n
{\displaystyle B={\begin{pmatrix}-4&1&0&\ldots &0\\1&-4&1&\ldots &0\\\vdots &\ddots &\ddots &\ddots &1\\0&\ldots &0&1&-4\end{pmatrix}},\quad B\in {\mathbb {R} }^{n\times n}}
Einheitsmatrix
I
=
E
n
∈
R
n
×
n
{\displaystyle I=E_{n}\in {\mathbb {R} }^{n\times n}}
u
|
∂
D
=
g
≠
0
{\displaystyle u|_{\partial D}=g\neq 0}
f
→
h
{\displaystyle {\vec {f}}_{h}}
Aufgabe:
Seien Funktionen
C
(
y
)
,
D
(
y
)
,
A
(
x
)
,
B
(
x
)
{\displaystyle C(y),\ D(y),\ A(x),\ B(x)}
∂
D
,
D
=
[
a
,
b
]
×
[
c
,
d
]
{\displaystyle \partial D,\ D=[a,b]\times [c,d]}
u
(
x
0
,
y
)
=
u
(
a
,
y
)
=
C
(
y
)
,
{\displaystyle u(x_{0},y)=u(a,y)=C(y),}
u
(
x
n
+
1
,
y
)
=
u
(
b
,
y
)
=
D
(
y
)
,
{\displaystyle u(x_{n+1},y)=u(b,y)=D(y),}
u
(
x
,
y
0
)
=
u
(
x
,
c
)
=
A
(
x
)
,
{\displaystyle u(x,y_{0})=u(x,c)=A(x),}
u
(
x
,
y
m
+
1
)
=
u
(
x
,
d
)
=
B
(
x
)
.
{\displaystyle u(x,y_{m+1})=u(x,d)=B(x).}
f
→
h
{\displaystyle {\vec {f}}_{h}}
Im Neumann-Problem mit äquidistanten Punktegitter wird die Anwendung der zweidimensionaler Differenzenquotienten in dasselbe Stern-Approximationsschema resultieren wie bei Dirichlet-Problem,
lediglich wird die Behandlung den Randbedingungen zu veränderter Struktur einiger Blöcke der tridiagonaler Matrix nach der Aufstellung des linearen Gleichungssystem führen.
Neumann-Randbedingungen auf dem Rechteck [ Bearbeiten ] Seien die Ableitungen der unbekannten Funktion in den Randpunkten des Rechtecks gegeben:
linker Rand:
∂
u
∂
n
→
(
x
0
,
y
j
)
=
α
,
n
→
=
(
−
1
,
0
)
T
,
{\displaystyle {\frac {\partial u}{\partial {\vec {n}}}}(x_{0},y_{j})=\alpha ,\ \quad {\vec {n}}=(-1,0)^{T},}
rechter Rand:
∂
u
∂
n
→
(
x
n
+
1
,
y
j
)
=
β
,
n
→
=
(
1
,
0
)
T
,
j
=
1
,
…
m
,
{\displaystyle {\frac {\partial u}{\partial {\vec {n}}}}(x_{n+1},y_{j})=\beta ,\ \quad {\vec {n}}=(1,0)^{T},\ j=1,\ldots m,}
unterer Rand:
∂
u
∂
n
→
(
x
i
,
y
0
)
=
γ
,
n
→
=
(
0
,
−
1
)
T
,
{\displaystyle {\frac {\partial u}{\partial {\vec {n}}}}(x_{i},y_{0})=\gamma ,\ \quad {\vec {n}}=(0,-1)^{T},}
oberer Rand:
∂
u
∂
n
→
(
x
i
,
y
m
+
1
)
=
δ
,
n
→
=
(
0
,
1
)
T
,
i
=
1
,
…
n
,
{\displaystyle {\frac {\partial u}{\partial {\vec {n}}}}(x_{i},y_{m+1})=\delta ,\ \quad {\vec {n}}=(0,1)^{T},\ i=1,\ldots n,}
wobei
∂
u
∂
n
→
≡
∇
u
⋅
n
→
=
∂
u
∂
x
n
1
+
∂
u
∂
y
n
2
.
{\displaystyle {\frac {\partial u}{\partial {\vec {n}}}}\equiv \nabla u\cdot {\vec {n}}={\frac {\partial u}{\partial x}}n_{1}+{\frac {\partial u}{\partial y}}n_{2}.}
Speziell
∂
u
∂
n
→
=
±
∂
u
∂
x
{\displaystyle {\frac {\partial u}{\partial {\vec {n}}}}=\pm {\frac {\partial u}{\partial x}}}
±
∂
u
∂
y
{\displaystyle \pm {\frac {\partial u}{\partial y}}}
Bei der Anwendung der einseitigen Differenzenquotienten, analog wie 1-dimensionalem Fall
muss der Vektor den Unbekannten
u
→
h
{\displaystyle {\vec {u}}_{h}}
u
0
,
j
,
u
n
+
1
,
j
,
u
i
,
0
,
u
i
,
m
+
1
{\displaystyle {u}_{0,j},\ {u}_{n+1,j},\ {u}_{i,0},\ {u}_{i,m+1}}
linker Rand: den vorwärts -Differenzenquotient
D
h
,
x
+
u
(
x
0
,
y
j
)
=
u
1
,
j
−
u
0
,
j
h
≈
∂
u
∂
x
(
x
0
,
y
j
)
)
≡
−
α
{\displaystyle D_{h,x}^{+}u(x_{0},y_{j})={\frac {u_{1,j}-u_{0,j}}{h}}\approx {\frac {\partial u}{\partial x}}(x_{0},y_{j}))\equiv -\alpha }
rechter Rand: den rückwärts -Differenzenquotient
D
h
,
x
−
u
(
x
n
+
1
,
y
j
)
=
u
n
+
1
,
j
−
u
n
,
j
h
≈
∂
u
∂
x
(
x
n
+
1
,
y
j
)
≡
β
,
j
=
1
,
…
m
{\displaystyle D_{h,x}^{-}u(x_{n+1},y_{j})={\frac {u_{n+1,j}-u_{n,j}}{h}}\approx {\frac {\partial u}{\partial x}}(x_{n+1},y_{j})\equiv \beta ,\ j=1,\ldots m}
unterer Rand: den vorwärts -Differenzenquotient
D
h
,
y
+
u
(
x
i
,
y
0
)
=
u
i
,
1
−
u
i
,
0
h
≈
∂
u
∂
y
(
x
i
,
y
0
)
)
≡
−
γ
{\displaystyle D_{h,y}^{+}u(x_{i},y_{0})={\frac {u_{i,1}-u_{i,0}}{h}}\approx {\frac {\partial u}{\partial y}}(x_{i},y_{0}))\equiv -\gamma }
oberer Rand: den rückwärts -Differenzenquotient
D
h
,
y
−
u
(
x
i
,
y
m
+
1
)
=
u
i
,
m
+
1
−
u
i
,
m
h
≈
∂
u
∂
y
(
x
i
,
y
m
+
1
)
)
≡
δ
,
i
=
1
,
…
n
.
{\displaystyle D_{h,y}^{-}u(x_{i},y_{m+1})={\frac {u_{i,m+1}-u_{i,m}}{h}}\approx {\frac {\partial u}{\partial y}}(x_{i},y_{m+1}))\equiv \delta ,\ i=1,\ldots n.}
(Hier wurde direkt die obige Neumann-Randbedingung für ein Rechteckgebiet
D
=
[
a
,
b
]
×
[
c
,
d
]
{\displaystyle \ D=[a,b]\times [c,d]}
Nach der Einordnung der unbekannter Werte in den Lösungsvektor wie obenbeschrieben (siehe Assemblierung ) ergibt sich
wie zuvor eine erweiterte Blocktridiagonale Systemmatrix
A
~
h
∈
R
(
n
+
2
)
(
m
+
2
)
×
(
n
+
2
)
(
m
+
2
)
{\displaystyle {\tilde {A}}_{h}\in {\mathbb {R} }^{(n+2)(m+2)\times (n+2)(m+2)}}
erweitert um die 0-te und m+1-te Blockzeile für die Approximation der Ableitung nach y in den Gitterpunkten am oberem und unterem Rand,
die Blöcke der Matrix:
B
,
I
,
0
{\displaystyle {B,\ I},\ 0}
B
{\displaystyle B}
A
~
h
{\displaystyle {\tilde {A}}_{h}}
Neumann-Problem in einer Raumdimension identisch.
Aufgabe: Stellen Sie die Systemmatrix
A
~
h
{\displaystyle {\tilde {A}}_{h}}
Wir untersuchen, unter welcher Vorausstetzungen und mit welcher Approximationsgüte Randwertproblem für Poissongleichung ,
u
i
{\displaystyle u_{i}}
u
i
,
j
{\displaystyle u_{i,j}}
u
→
h
{\displaystyle {\vec {u}}_{h}}
zu der exakten Lösung in den Gitterpunkten
u
(
x
i
)
{\displaystyle u(x_{i})}
u
(
x
i
,
y
j
)
{\displaystyle u(x_{i},y_{j})}
Im folgenden bezeichnen wir mit
u
→
{\displaystyle {\vec {u}}}
x
i
i
=
1
,
…
N
{\displaystyle x_{i}\ i=1,\ldots N}
(
x
i
,
y
j
)
i
=
1
,
…
N
,
j
=
1
,
…
M
{\displaystyle (x_{i},y_{j})\ i=1,\ldots N,\ j=1,\ldots M}
Assemblierung ).
Wir untersuchen den Unterschied der exakten und der numerischen Lösung in einer geeigneter Vektornorm auf
R
N
{\displaystyle {\mathbb {R} }^{N}}
‖
u
→
−
u
→
h
‖
,
u
→
=
(
u
(
x
1
)
,
…
u
(
x
N
)
)
T
,
u
→
h
=
(
u
1
,
…
u
N
)
T
,
u
i
≈
u
(
x
i
)
.
{\displaystyle \displaystyle \|{\vec {u}}-{\vec {u}}_{h}\|,\quad {\vec {u}}=(u(x_{1}),\ldots u(x_{N}))^{T},\ {\vec {u}}_{h}=(u_{1},\ldots u_{N})^{T},\ u_{i}\approx u(x_{i}).}
‖
u
→
−
u
→
h
‖
→
0
{\displaystyle \|{\vec {u}}-{\vec {u}}_{h}\|\to 0}
h
→
0
{\displaystyle h\to 0}
den Eigenschaften der Systemmatrix
A
h
{\displaystyle A_{h}}
der Approximationsgüte des Approximationschema (der Differenzenquotienten ) abhängig ist.
A
h
{\displaystyle A_{h}}
u
→
h
{\displaystyle {\vec {u}}_{h}}
A
h
u
→
h
=
f
→
h
=:
f
→
=
(
f
(
x
1
)
,
…
,
(
x
N
)
)
T
{\displaystyle A_{h}{\vec {u}}_{h}={\vec {f}}_{h}=:{\vec {f}}=(f(x_{1}),\ldots ,(x_{N}))^{T}}
Unter Anwendung der Verträglichkeit der Matrixnorm folgt
‖
u
→
−
u
→
h
‖
=
‖
A
h
−
1
A
h
u
→
−
A
h
−
1
f
→
‖
=
‖
A
h
−
1
(
A
h
u
→
−
f
→
)
‖
≤
‖
|
A
h
−
1
‖
|
.
‖
A
h
u
→
−
f
→
‖
,
{\displaystyle \displaystyle \|{\vec {u}}-{\vec {u}}_{h}\|=\|A_{h}^{-1}A_{h}{\vec {u}}-A_{h}^{-1}{\vec {f}}\|=\|A_{h}^{-1}(A_{h}{\vec {u}}-{\vec {f}})\|\leq \||A_{h}^{-1}\||.\|A_{h}{\vec {u}}-{\vec {f}}\|,}
wobei
‖
|
⋅
‖
|
{\displaystyle \||\cdot \||}
Vektornorm-induzierte (natürliche) Matrixnorm bezeichnet.
Folglich ist die Konvergenz
‖
u
→
−
u
→
h
‖
→
0
{\displaystyle \|{\vec {u}}-{\vec {u}}_{h}\|\to 0}
die Norm von
A
h
−
1
{\displaystyle A_{h}^{-1}}
h
{\displaystyle h}
‖
|
A
h
−
1
‖
|
≤
r
,
r
∈
R
{\displaystyle \||A_{h}^{-1}\||\leq r,\ r\in {\mathbb {R} }}
(Stabilität)
‖
A
h
u
→
−
f
→
‖
→
0
{\displaystyle \|A_{h}{\vec {u}}-{\vec {f}}\|\to 0}
h
→
0
{\displaystyle h\to 0}
A
h
u
→
h
=
f
→
{\displaystyle A_{h}{\vec {u}}_{h}={\vec {f}}}
Originalproblem ,
−
Δ
u
→
=
f
→
{\displaystyle -\Delta {\vec {u}}={\vec {f}}}
(Konsistenz) .Der zweite Punkt beschreibt, dass Restriktion der exakten Lösung auf die Gitterpunkte das Approximationschema annäherungsweise erfüllt.
Wir setzen voraus, dass die Funktion der rechten Seite
f
{\displaystyle f}
Definition: (Konsistenzordnung) die Poisson Randwertaufgabe hat bezüglich einer Vektornorm in
R
N
{\displaystyle {\mathbb {R} }^{N}}
p
{\displaystyle p}
u
→
{\displaystyle {\vec {u}}}
C
∈
R
+
{\displaystyle C\in {\mathbb {R} }_{+}}
‖
A
h
u
→
−
f
→
‖
=
‖
A
h
u
→
+
Δ
u
→
‖
≤
C
.
h
p
{\displaystyle \displaystyle \|A_{h}{\vec {u}}-{\vec {f}}\|=\|A_{h}{\vec {u}}+\Delta {\vec {u}}\|\leq C.h^{p}}
Konsistenz elliptischer Randwertprobleme [ Bearbeiten ]
Den Begriff der Konsistenz, Stabilität und schließlich der Beweis der Konvergenz für das FDM- Verfahren kann man auf
elliptische Randwertprobleme mit elliptischen Differenzialoperator
L
:
u
→
L
(
u
)
{\displaystyle L:u\to L(u)}
u
{\displaystyle u}
Vorausgesetzt
f
,
c
:
D
→
R
,
b
:
D
→
R
n
,
{\displaystyle f,c:D\to {\mathbb {R} },\ b:D\to {\mathbb {R} }^{n},}
R
n
{\displaystyle {\mathbb {R} }^{n}}
c
≥
0
{\displaystyle c\geq 0}
L
(
u
)
:=
−
Δ
u
(
x
)
+
b
(
x
)
⋅
∇
u
(
x
)
+
c
(
x
)
u
(
x
)
=
f
(
x
)
,
x
∈
D
⊂
R
n
,
{\displaystyle \displaystyle L(u):=-\Delta u(x)+b(x)\cdot \nabla u(x)+c(x)u(x)=f(x),\ \ x\in D\subset {\mathbb {R} }^{n},}
u
(
x
)
=
0
,
x
∈
∂
D
{\displaystyle u(x)=0,\ \ x\in \partial D}
Approximationschema des elliptischen Operators [ Bearbeiten ] Das entsprechende Approximationsschema
L
h
(
u
)
{\displaystyle L_{h}(u)}
L
(
u
)
{\displaystyle L(u)}
D
∈
R
2
{\displaystyle D\in {\mathbb {R} }^{2}}
Stern-Approximationsschema
für das Laplace Operator anhand der zweiten Differenzenquotienten
D
h
2
{\displaystyle D_{h}^{2}}
A
h
{\displaystyle A_{h}}
∇
u
=
(
∂
x
1
u
,
…
,
∂
x
n
u
)
T
{\displaystyle \nabla u=(\partial _{x_{1}}u,\ldots ,\partial _{x_{n}}u)^{T}}
D
h
±
,
D
h
{\displaystyle D_{h}^{\pm },\ D_{h}}
erste Differenzenquotient .
‖
L
h
u
→
−
f
→
‖
=
‖
L
h
u
→
−
L
(
u
→
)
‖
≤
C
.
h
p
.
{\displaystyle \displaystyle \|L_{h}{\vec {u}}-{\vec {f}}\|=\|L_{h}{\vec {u}}-L({\vec {u}})\|\leq C.h^{p}.}
Sei
u
∈
C
4
(
D
)
{\displaystyle u\in C^{4}(D)}
L
(
u
)
=
f
{\displaystyle L(u)=f}
L
h
{\displaystyle L_{h}}
p
=
1
{\displaystyle p=1}
D
h
±
{\displaystyle D_{h}^{\pm }}
p
=
2
{\displaystyle p=2}
D
h
{\displaystyle D_{h}}
∇
u
{\displaystyle \nabla u}
⋄
{\displaystyle \quad \diamond }
Beweis: basiert auf der Approximationsgüte der ersten und der zweiten Differenzenquotienten (Lemma 1 und 2). Für das Approximationsschema
A
h
{\displaystyle A_{h}}
A
h
u
→
=
−
Δ
u
→
+
O
(
h
2
)
{\displaystyle A_{h}{\vec {u}}=-\Delta {\vec {u}}+{\cal {O}}(h^{2})}
L
h
{\displaystyle L_{h}}
L
h
u
→
=
L
(
u
→
)
+
O
(
h
2
)
+
O
(
h
)
=
L
(
u
→
)
+
O
(
h
)
{\displaystyle L_{h}{\vec {u}}=L({\vec {u}})+{\cal {O}}(h^{2})+{\cal {O}}(h)=L({\vec {u}})+{\cal {O}}(h)}
L
h
u
→
=
L
(
u
→
)
+
O
(
h
2
)
{\displaystyle L_{h}{\vec {u}}=L({\vec {u}})+{\cal {O}}(h^{2})}
◻
{\displaystyle \square }
Im Fall
b
=
c
=
0
,
D
∈
R
2
−
{\displaystyle b=c=0,\ D\in {\mathbb {R} }^{2}-}
L
h
=
A
h
{\displaystyle L_{h}=A_{h}}
p
=
2
{\displaystyle p=2}
Im Fall dass
D
∈
R
{\displaystyle D\in {\mathbb {R} }}
Lemma 2 in der Maximum-Vektornorm
‖
⋅
‖
∞
{\displaystyle \|\cdot \|_{\infty }}
u
→
,
f
→
∈
R
N
{\displaystyle {\vec {u}},\ {\vec {f}}\in {\mathbb {R} }^{N}}
‖
A
h
u
→
−
f
→
‖
∞
=
‖
A
h
u
→
+
u
→
″
‖
∞
=
max
i
|
−
D
h
2
u
(
x
i
)
+
u
″
(
x
i
)
|
≤
h
2
12
max
x
∈
D
|
u
(
I
V
)
(
x
)
|
=
h
2
12
max
x
∈
D
|
f
″
(
x
)
|
.
{\displaystyle \|A_{h}{\vec {u}}-{\vec {f}}\|_{\infty }=\|A_{h}{\vec {u}}+{\vec {u}}''\|_{\infty }=\max _{i}\left|-D_{h}^{2}u(x_{i})+u''(x_{i})\right|\leq {\frac {h^{2}}{12}}\max _{x\in D}|{u}^{(IV)}(x)|={\frac {h^{2}}{12}}\max _{x\in D}|{f}''(x)|.}
Damit ist die Konstante
C
{\displaystyle C}
C
=
1
12
max
x
∈
D
|
f
″
(
x
)
|
.
{\displaystyle C={\frac {1}{12}}\max _{x\in D}|{f}''(x)|.}
Definition: (Stabilität)
L
(
u
(
x
)
)
=
f
(
x
)
,
x
∈
D
⊂
R
n
,
{\displaystyle \displaystyle L(u(x))=f(x),\ \ x\in D\subset {\mathbb {R} }^{n},}
u
(
x
)
=
0
,
x
∈
∂
D
{\displaystyle u(x)=0,\ \ x\in \partial D}
stabil (bezüglich einer Vektornorm
‖
⋅
‖
{\displaystyle \|\cdot \|}
C
,
h
0
{\displaystyle C,h_{0}}
C
,
h
0
∈
R
+
{\displaystyle C,h_{0}\in {\mathbb {R} }_{+}}
L
h
{\displaystyle L_{h}}
‖
|
L
h
−
1
‖
|
≤
C
{\displaystyle \||L_{h}^{-1}\||\leq C}
0
<
h
<
h
0
{\displaystyle 0<h<h_{0}}
Die Untersuchung der Stabilität anhand der Konstruktion der inversen Matrix
L
h
−
1
{\displaystyle L_{h}^{-1}}
Monotonie Eigenschaften der Matrix
L
h
{\displaystyle L_{h}}
Bemerkung:
Die Stabilitätsbedingung garantiert auch die Beschränkheit der numerischen Lösung als Lösung des linearen Systems
L
h
u
→
h
=
f
→
{\displaystyle L_{h}{\vec {u}}_{h}={\vec {f}}}
‖
u
→
h
‖
=
‖
L
h
−
1
f
→
‖
≤
‖
|
L
h
−
1
‖
|
.
‖
f
→
‖
{\displaystyle \|{\vec {u}}_{h}\|=\|L_{h}^{-1}{\vec {f}}\|\leq \||L_{h}^{-1}\||.\|{\vec {f}}\|}
‖
|
L
h
−
1
‖
|
{\displaystyle \||L_{h}^{-1}\||}
Eine reguläre Matrix
A
∈
R
N
×
N
{\displaystyle A\in {\mathbb {R} }^{N\times N}}
a
i
j
≤
0
{\displaystyle a_{ij}\leq 0}
i
≠
j
{\displaystyle i\neq j}
und
(
A
−
1
)
i
j
≥
0
{\displaystyle (A^{-1})_{ij}\geq 0}
A
−
1
≥
0
{\displaystyle A^{-1}\geq 0}
M-Matrix , oder Monotonie-Matrix .
Für eine M-Matrix
A
∈
R
N
×
N
{\displaystyle A\in {\mathbb {R} }^{N\times N}}
x
→
,
y
→
∈
R
N
{\displaystyle {\vec {x}},{\vec {y}}\in {\mathbb {R} }^{N}}
x
→
≤
y
→
⟹
A
−
1
x
→
≤
A
−
1
y
→
{\displaystyle {\vec {x}}\leq {\vec {y}}\implies A^{-1}{\vec {x}}\leq A^{-1}{\vec {y}}}
Beweis:
Ist
x
j
≤
y
j
∀
j
=
1
,
…
N
⟹
∑
j
=
1
N
(
A
−
1
)
i
j
x
j
≤
∑
j
=
1
N
(
A
−
1
)
i
j
y
j
,
{\displaystyle {x}_{j}\leq {y}_{j}\ \ \forall j=1,\ldots N\ \implies \ \sum _{j=1}^{N}(A^{-1})_{ij}x_{j}\leq \sum _{j=1}^{N}(A^{-1})_{ij}y_{j},\ }
(
A
−
1
)
i
j
≥
0
◻
.
{\displaystyle (A^{-1})_{ij}\geq 0\ \ \square .}
In diesem Abschnitt werden die Kriterien für Tridiagonalmatrizen wie die Systemmatrix
A
h
{\displaystyle A_{h}}
und die Matrix
L
h
{\displaystyle L_{h}}
elliptischen Randwertproblems in einer Raumdimension
x
∈
R
{\displaystyle x\in {\mathbb {R} }}
Satz: Monotonie tridiagonaler Matrizen [ Bearbeiten ] Jede irreduzibel diagonaldominante Tridiagonalmatrix mit positiven Diagonalelementen und negativen Nebendiagonalelementen ist eine M-Matrix.
⋄
{\displaystyle \quad \diamond }
Beweis: siehe [ 1]
◻
{\displaystyle \square }
Bemerkung:
Die Matrix
A
h
{\displaystyle A_{h}}
für das Dirichlet Randwertproblem is eine M-Matrix.
Beweis:
A
h
{\displaystyle A_{h}}
|
a
i
,
i
|
>
|
a
i
,
i
±
1
|
{\displaystyle |a_{i,i}|>|a_{i,i\pm 1}|}
A
h
{\displaystyle A_{h}}
◻
{\displaystyle \square }
Die Matrix
L
h
{\displaystyle L_{h}}
ersten zentralen Differenzenquotienten
D
h
{\displaystyle D_{h}}
für
u
′
(
x
i
)
,
i
=
1
,
…
N
{\displaystyle u'(x_{i}),\ i=1,\ldots N}
0
<
h
<
h
0
≡
2
max
x
∈
D
|
b
(
x
)
|
{\displaystyle 0<h<h_{0}\equiv {\frac {2}{\max _{x\in D}|b(x)|}}}
Beweis:
L
h
=
1
h
2
(
d
1
s
1
0
…
0
r
2
d
2
s
2
⋮
⋮
⋱
⋱
⋱
0
…
r
N
d
N
)
{\displaystyle L_{h}={\frac {1}{h^{2}}}{\begin{pmatrix}d_{1}&s_{1}&0&\ldots &0\\r_{2}&d_{2}&s_{2}&&\vdots \\\vdots &\ddots &\ddots &\ddots &\\0&&\ldots &r_{N}&d_{N}\end{pmatrix}}}
d
i
=
2
+
h
2
c
(
x
i
)
,
r
i
=
−
1
−
h
2
b
(
x
i
)
,
s
i
=
−
1
+
h
2
b
(
x
i
)
.
{\displaystyle {\begin{matrix}d_{i}=2+h^{2}c(x_{i}),\\r_{i}=-1-{\frac {h}{2}}b(x_{i}),\\s_{i}=-1+{\frac {h}{2}}b(x_{i}).\end{matrix}}}
|
h
2
b
(
x
i
)
|
<
1
,
i
=
1
,
…
N
{\displaystyle \left|{\frac {h}{2}}b(x_{i})\right|<1,\ i=1,\ldots N}
r
i
,
s
i
≠
0
{\displaystyle r_{i},\ s_{i}\neq 0}
⟹
L
h
{\displaystyle \implies L_{h}}
L
h
{\displaystyle L_{h}}
1
h
2
(
|
r
i
|
+
|
s
i
|
)
=
2
h
2
≤
d
i
h
2
{\displaystyle {\frac {1}{h^{2}}}(|r_{i}|+|s_{i}|)={\frac {2}{h^{2}}}\leq {\frac {d_{i}}{h^{2}}}}
c
(
x
)
≥
0
,
i
=
2
,
…
N
−
1
,
{\displaystyle c(x)\geq 0,\ i=2,\ldots N-1,}
i
=
1
,
N
{\displaystyle i=1,N}
◻
{\displaystyle \ \square }
[ Bearbeiten ]
Hier befassen wir ist mit der Frage wie aus der Monotonie Eigenschaft die Stabilität des Approximationsschemas folgt.
Die Beschränkheit der Matrix
L
h
−
1
{\displaystyle L_{h}^{-1}}
‖
|
⋅
‖
|
∞
{\displaystyle \||\cdot \||_{\infty }}
Zeilensummennorm ), die von der Maximum-Vektornom
‖
⋅
‖
∞
{\displaystyle \|\cdot \|_{\infty }}
[ 2]
Wir untersuchen folgendes Randwertproblem: gegeben sei
b
∈
C
2
[
0
,
1
]
{\displaystyle b\in C^{2}[0,1]}
−
w
″
(
x
)
+
b
(
x
)
w
′
(
x
)
=
1
,
{\displaystyle -w''(x)+b(x)w'(x)=1,}
w
(
0
)
=
w
(
1
)
=
0.
{\displaystyle \ w(0)=w(1)=0.}
Sei die Lösungsfunktion
w
∈
C
4
[
0
,
1
]
{\displaystyle w\in C^{4}[0,1]}
Lemma 3 :
Die Lösung
w
{\displaystyle w}
w
≥
0
∀
x
∈
[
0
,
1
]
{\displaystyle w\geq 0\ \forall x\in [0,1]}
Beweis:
w
≠
0
{\displaystyle w\neq 0}
w
=
0
{\displaystyle w=0}
Wäre
w
<
0
{\displaystyle w<0}
w
{\displaystyle w}
x
0
∈
(
0
,
1
)
{\displaystyle x_{0}\in (0,1)}
w
′
(
x
0
)
=
0
{\displaystyle w'(x_{0})=0}
w
″
(
x
0
)
≥
0
{\displaystyle w''(x_{0})\geq 0}
Damit erhalten wir aus der obigen Differenzialgleichung
−
w
″
(
x
0
)
+
b
(
x
0
)
w
′
(
x
0
)
=
−
w
″
(
x
0
)
=
1
⟹
w
″
(
x
0
)
≤
0
{\displaystyle -w''(x_{0})+b(x_{0})w'(x_{0})=-w''(x_{0})=1\implies w''(x_{0})\leq 0}
◻
{\displaystyle \square }
L
h
−
1
{\displaystyle L_{h}^{-1}}
[ Bearbeiten ]
Sei zusätzlich eine stetige nichtnegative Funktion
c
∈
C
[
0
,
1
]
,
c
≥
0
{\displaystyle c\in C[0,1],\ c\geq 0}
Für den elliptischen Operator mit Funktion
b
{\displaystyle b}
L
(
w
)
=
−
w
″
+
b
w
′
+
c
w
≥
1
,
{\displaystyle L(w)=-w''+bw'+cw\geq 1,}
Aus dem Satz über die Konsistenz des Approximationsschema für elliptische Operatoren erhalten wir für das Approximationsschema
L
h
{\displaystyle L_{h}}
L
{\displaystyle L}
w
→
{\displaystyle {\vec {w}}}
w
{\displaystyle {w}}
‖
L
h
w
→
−
L
(
w
→
)
‖
∞
≤
C
.
h
2
.
{\displaystyle \|L_{h}{\vec {w}}-L({\vec {w}})\|_{\infty }\leq C.h^{2}.}
|
(
L
h
w
→
−
L
(
w
→
)
)
i
|
≤
C
h
2
{\displaystyle |(L_{h}{\vec {w}}-L({\vec {w}}))_{i}|\leq Ch^{2}}
i
=
1
…
,
N
{\displaystyle i=1\ldots ,N}
L
(
w
→
)
+
C
h
2
1
≥
L
h
w
→
≥
L
(
w
→
)
−
C
h
2
1
,
1
=
(
1
,
…
,
1
)
T
.
{\displaystyle L({\vec {w}})+Ch^{2}{\bf {1}}\geq L_{h}{\vec {w}}\geq L({\vec {w}})-Ch^{2}{\bf {1}},\quad {\bf {1}}=(1,\ldots ,1)^{T}.}
Da
L
(
w
)
≥
1
,
{\displaystyle L(w)\geq {\bf {1}},}
L
h
w
→
≥
1
−
C
h
2
1
.
{\displaystyle L_{h}{\vec {w}}\geq {\bf {1}}-Ch^{2}{\bf {1}}.}
Folglich gilt für ausreichend kleine
h
<
h
0
{\displaystyle h<h_{0}}
h
0
{\displaystyle h_{0}}
Folgerung 2
1
2
1
≤
L
h
w
→
.
{\displaystyle {\frac {1}{2}}{\bf {1}}\leq L_{h}{\vec {w}}.}
Da
L
h
{\displaystyle L_{h}}
Eigenschaft der Monotonie der Matrix
L
h
{\displaystyle L_{h}}
1
2
L
h
−
1
1
≤
w
→
.
{\displaystyle {\frac {1}{2}}L_{h}^{-1}{\bf {1}}\leq {\vec {w}}.}
Weil
L
h
−
1
{\displaystyle L_{h}^{-1}}
‖
|
L
h
−
1
‖
|
∞
=
‖
L
h
−
1
1
‖
∞
{\displaystyle \||L_{h}^{-1}\||_{\infty }=\|L_{h}^{-1}{\bf {1}}\|_{\infty }}
‖
|
L
h
−
1
‖
|
∞
≤
2
‖
w
→
‖
∞
≤
2
max
x
∈
[
0
,
1
]
|
w
|
.
{\displaystyle \||L_{h}^{-1}\||_{\infty }\leq 2\|{\vec {w}}\|_{\infty }\leq 2\max _{x\in [0,1]}|w|.}
Nach der Voraussetzung (für die zweite Konsistenzordnung) ist
w
{\displaystyle w}
max
x
∈
[
0
,
1
]
|
w
|
{\displaystyle \max _{x\in [0,1]}|w|}
‖
|
L
h
−
1
‖
|
∞
≤
K
∈
R
+
.
{\displaystyle \||L_{h}^{-1}\||_{\infty }\leq K\in {\mathbb {R} }_{+}.}
Wir haben bewiesen:
L
h
{\displaystyle L_{h}}
[ Bearbeiten ] Sei
b
∈
C
2
[
0
,
1
]
,
c
∈
C
[
0
,
1
]
,
c
≥
0
{\displaystyle b\in C^{2}[0,1],\ c\in C[0,1],\ c\geq 0}
D
h
u
(
x
)
≈
u
′
(
x
)
{\displaystyle D_{h}u(x)\approx u'(x)}
L
h
u
→
h
=
f
→
{\displaystyle L_{h}{\vec {u}}_{h}={\vec {f}}}
Systemmatrix
L
h
{\displaystyle L_{h}}
elliptische Randwertprobleme stabil.
⋄
{\displaystyle \quad \diamond }
Hauptsatz: Zweite Konvergenzordnung des FDM-Verfahrens [ Bearbeiten ]
Sei
u
∈
C
4
[
0
,
1
]
{\displaystyle u\in C^{4}[0,1]}
elliptischen Randwertproblems ,
u
→
{\displaystyle {\vec {u}}}
u
→
h
{\displaystyle {\vec {u}}_{h}}
L
h
u
→
h
=
f
→
:=
f
→
h
{\displaystyle L_{h}{\vec {u}}_{h}={\vec {f}}:={\vec {f}}_{h}}
L
h
{\displaystyle L_{h}}
das Approximationschema mit zentralen Differenzenquotienten
D
h
u
(
x
)
≈
u
′
(
x
)
{\displaystyle D_{h}u(x)\approx u'(x)}
Dann gilt für eine hinreichend kleine Schrittweite
h
{\displaystyle h}
zweite Konvergenzordnung:
‖
u
→
−
u
→
h
‖
∞
≤
C
h
2
{\displaystyle \|{\vec {u}}-{\vec {u}}_{h}\|_{\infty }\leq Ch^{2}}
mit einer Konstante
C
>
0
{\displaystyle C>0}
⋄
{\displaystyle \quad \diamond }
Blocktridiagonaler Systemmatrix untersuchen.
SW10: Numerische Diskretisierung der Reaktionsdiffusionsgleichung mit FDM [ Bearbeiten ] Im folgenden wir die numerische Diskretisierung des Reaktionsdiffusionsprozesses in der Populationsdynamik beschrieben.
∂
t
u
(
x
,
t
)
−
d
i
v
(
c
(
x
)
∇
u
(
x
,
t
)
)
=
f
(
u
(
x
,
t
)
)
.
{\displaystyle \partial _{t}u(x,t)-div\ (c(x)\nabla u(x,t))=f(u(x,t)).}
Hier beschreibt die unbekannte Funktion
u
{\displaystyle u}
Reaktionsterm
f
=
f
(
u
)
{\displaystyle f=f(u)}
Kompartimentmodellen dar.
Alternativ kann
f
=
f
(
u
)
{\displaystyle f=f(u)}
unbeschränktes Wachstum .
[ Bearbeiten ] Zuerst wird Neumann Randwertproblem für die zeitabhängige homogene Diffusionsgleichung auf einem Rechteckgebiet D betrachtet.
∂
t
u
(
x
,
t
)
−
d
i
v
(
c
(
x
)
∇
u
(
x
,
t
)
)
=
0
,
x
∈
D
⊂
R
2
,
t
∈
(
t
0
,
T
)
,
{\displaystyle \quad \partial _{t}u(x,t)-div\ (c(x)\nabla u(x,t))=0,\ x\in \ D\subset \mathbb {R} ^{2},\ t\in (t_{0},T),}
∂
u
(
x
)
∂
n
→
≡
∇
u
⋅
n
→
=
g
(
x
)
x
∈
∂
D
.
{\displaystyle \quad {\frac {\partial u(x)}{\partial {\vec {n}}}}\equiv \nabla u\cdot {\vec {n}}=g(x)\quad x\in \partial D.}
Im folgenden nehmen wir an, dass der Diffusionskoeffizient ist konstant,
c
(
x
)
=
c
{\displaystyle c(x)=c}
∂
t
u
(
x
,
t
)
−
c
Δ
u
(
x
,
t
)
=
0
{\displaystyle \partial _{t}u(x,t)-c\Delta u(x,t)=0}
[ Bearbeiten ] Mithilfe der räumlichen Semidiskretisierung des Laplace Operators mit Finite-Differenzenverfahren unter Beachtung der homogenen Neumann Randbedingungen
α
=
β
=
γ
=
δ
=
0
{\displaystyle \alpha =\beta =\gamma =\delta =0}
Approximation der Richtungsableitungen erster Ordnung
erhält man für ein festes
t
∈
(
t
0
,
T
)
{\displaystyle t\in (t_{0},T)}
Stern-Approximationsschema
−
c
Δ
u
→
(
t
)
≈
A
h
u
→
h
{\displaystyle -c\Delta {\vec {u}}(t)\approx A_{h}{\vec {u}}_{h}}
hierbei ist
u
→
(
t
)
=
(
u
(
x
0
,
y
0
,
t
)
,
…
,
u
(
x
n
+
1
,
y
m
+
1
,
t
)
)
T
{\displaystyle {\vec {u}}(t)=(u(x_{0},y_{0},t),\ldots ,u(x_{n+1},y_{m+1},t))^{T}}
(
x
i
,
y
j
)
,
i
=
0
,
…
,
n
+
1
,
j
=
0
,
…
,
m
+
1
{\displaystyle (x_{i},y_{j}),\ i=0,\ldots ,n+1,\ j=0,\ldots ,m+1}
t
{\displaystyle t}
u
→
h
(
t
)
=
(
u
0
,
0
(
t
)
,
…
,
u
n
+
1
,
m
+
1
(
t
)
)
T
{\displaystyle {\vec {u}}_{h}(t)=(u_{0,0}(t),\ldots ,u_{n+1,m+1}(t))^{T}}
t
{\displaystyle t}
Die Matrix des Approximationsschema für Neumann Randbedingungen hat die Form:
A
h
=
−
c
h
2
(
−
h
I
h
I
…
0
I
~
B
I
~
⋮
⋮
⋱
⋱
⋱
0
…
h
I
−
h
I
)
,
{\displaystyle A_{h}={\frac {-c}{h^{2}}}{\begin{pmatrix}-hI&hI&&\ldots &0\\{\tilde {I}}&B&{\tilde {I}}&&\vdots \\\vdots &\ddots &\ddots &\ddots &\\0&&\ldots &hI&-hI\end{pmatrix}},}
B
=
(
−
h
h
0
…
0
1
−
4
1
…
0
⋮
⋱
⋱
⋱
0
…
1
−
4
1
0
…
0
h
−
h
)
,
I
~
=
(
0
…
0
0
1
0
…
0
⋮
⋱
⋱
⋱
⋮
0
…
0
1
0
0
…
0
)
I
~
,
B
∈
R
(
n
+
2
)
×
(
n
+
2
)
,
{\displaystyle B={\begin{pmatrix}-h&h&0&\ldots &0\\1&-4&1&\ldots &0\\\vdots &\ddots &\ddots &\ddots &\\0&\ldots &1&-4&1&\\0&\ldots &0&h&-h\end{pmatrix}},\quad {\tilde {I}}={\begin{pmatrix}0&&\ldots &&0\\0&1&0&\ldots &0\\\vdots &\ddots &\ddots &\ddots &\vdots \\0&\ldots &0&1&0\\0&&\ldots &&0\end{pmatrix}}\quad {\tilde {I}},B\in {\mathbb {R} }^{(n+2)\times (n+2)},}
Einheitsmatrix
I
=
E
n
∈
R
(
n
+
2
)
×
(
n
+
2
)
{\displaystyle I=E_{n}\in {\mathbb {R} }^{(n+2)\times (n+2)}}
d
d
t
u
→
h
(
t
)
=
−
A
h
u
→
h
(
t
)
{\displaystyle {\frac {d}{dt}}{\vec {u}}_{h}(t)=-A_{h}{\vec {u}}_{h}(t)}
Der Vektor der numerischen Lösung
u
→
h
{\displaystyle {\vec {u}}_{h}}
[ Bearbeiten ] [ Bearbeiten ] Der Reaktionsterm
f
(
u
(
x
,
y
,
t
)
)
{\displaystyle f(u(x,y,t))}
u
→
(
t
)
{\displaystyle {\vec {u}}(t)}
f
(
u
→
(
t
)
)
≈
F
(
u
→
h
(
t
)
)
:=
c
B
→
∗
u
→
h
(
t
)
∗
(
B
→
−
u
→
h
(
t
)
)
≡
c
(
u
0
,
0
B
0
,
0
(
B
0
,
0
−
u
0
,
0
)
⋮
u
n
+
1
,
m
+
1
B
n
+
1
,
m
+
1
(
B
n
+
1
,
m
+
1
−
u
n
+
1
,
m
+
1
)
)
(
t
)
,
{\displaystyle f({\vec {u}}(t))\approx F({\vec {u}}_{h}(t)):={\frac {c}{\vec {B}}}*{\vec {u}}_{h}(t)*({\vec {B}}-{\vec {u}}_{h}(t))\equiv c{\begin{pmatrix}{\frac {u_{0,0}}{B_{0,0}}}(B_{0,0}-u_{0,0})\\\vdots \\{\frac {u_{n+1,m+1}}{B_{n+1,m+1}}}(B_{n+1,m+1}-u_{n+1,m+1})\end{pmatrix}}(t),}
wobei Vektor
B
→
=
(
B
0
,
0
,
…
,
B
n
+
1
,
m
+
1
)
T
{\displaystyle {\vec {B}}=(B_{0,0},\ldots ,B_{n+1,m+1})^{T}}
(
B
)
i
,
j
=
B
(
x
i
,
y
j
)
{\displaystyle (B)_{i,j}=B(x_{i},y_{j})}
∗
{\displaystyle *}
Bemerkung: die logistische Infektionsrate
k
:=
c
B
→
{\displaystyle k:={\frac {c}{\vec {B}}}}
Modifiziertes SIR Modell berechnet sich als Rate der Infektionsverbreitung bei einer Kontaktrate: Wahrscheinlichkeit des Kontakts eines Infizierten mit einem Anfälligen.
[ Bearbeiten ] Im Falle der räumlichen Modellierung der Dichte der aktuellen Infizierten
u
I
{\displaystyle u_{I}}
u
S
{\displaystyle u_{S}}
nach dem Prinzip des SIR-Kompartimentmodells
werden drei einander gekopelte Reaktionsdiffusionsgleichungen für die Dichtefunktionen
u
I
,
u
S
,
u
R
{\displaystyle u_{I},\ u_{S},\ u_{R}}
∂
t
u
S
(
x
,
t
)
−
d
i
v
(
c
(
x
)
∇
u
S
(
x
,
t
)
)
=
f
S
(
u
S
(
x
,
t
)
,
u
I
(
x
,
t
)
)
.
{\displaystyle \partial _{t}u_{S}(x,t)-div\ (c(x)\nabla u_{S}(x,t))=f_{S}(u_{S}(x,t),u_{I}(x,t)).}
∂
t
u
I
(
x
,
t
)
−
d
i
v
(
c
(
x
)
∇
u
I
(
x
,
t
)
)
=
f
I
(
u
S
(
x
,
t
)
,
u
I
(
x
,
t
)
)
.
{\displaystyle \partial _{t}u_{I}(x,t)-div\ (c(x)\nabla u_{I}(x,t))=f_{I}(u_{S}(x,t),u_{I}(x,t)).}
∂
t
u
R
(
x
,
t
)
−
d
i
v
(
c
(
x
)
∇
u
R
(
x
,
t
)
)
=
f
R
(
u
I
(
x
,
t
)
)
.
{\displaystyle \partial _{t}u_{R}(x,t)-div\ (c(x)\nabla u_{R}(x,t))=f_{R}(u_{I}(x,t)).}
Diese partielle Differentialgleichungen werden durch die reche Seiten
f
S
,
f
I
,
f
S
{\displaystyle f_{S},\ f_{I},\ f_{S}}
f
S
(
u
S
,
u
I
)
,
f
I
(
u
S
,
u
I
)
{\displaystyle f_{S}(u_{S},u_{I}),f_{I}(u_{S},u_{I})}
f
R
(
u
I
)
{\displaystyle f_{R}(u_{I})}
f
S
(
u
→
(
t
)
)
≈
F
S
(
u
→
h
(
t
)
)
:=
−
c
B
→
∗
u
I
→
h
(
t
)
∗
u
S
→
h
(
t
)
{\displaystyle f_{S}({\vec {u}}(t))\approx F_{S}({\vec {u}}_{h}(t)):=-{\frac {c}{\vec {B}}}*{\vec {u_{I}}}_{h}(t)*{\vec {u_{S}}}_{h}(t)}
f
I
(
u
→
(
t
)
)
≈
F
I
(
u
→
h
(
t
)
)
:=
c
B
→
∗
u
I
→
h
(
t
)
∗
u
S
→
h
(
t
)
−
w
u
I
→
h
(
t
)
,
{\displaystyle f_{I}({\vec {u}}(t))\approx F_{I}({\vec {u}}_{h}(t)):={\frac {c}{\vec {B}}}*{\vec {u_{I}}}_{h}(t)*{\vec {u_{S}}}_{h}(t)-w{\vec {u_{I}}}_{h}(t),}
f
R
(
u
→
(
t
)
)
≈
F
R
(
u
→
h
(
t
)
)
:=
w
u
I
→
h
(
t
)
,
{\displaystyle f_{R}({\vec {u}}(t))\approx F_{R}({\vec {u}}_{h}(t)):=w{\vec {u_{I}}}_{h}(t),}
wobei
w
{\displaystyle w}
Da die erste und zweite partielle Differentialgleichung für
u
I
,
u
S
{\displaystyle u_{I},\ u_{S}}
u
R
{\displaystyle u_{R}}
u
R
{\displaystyle u_{R}}
[ Bearbeiten ] Nach der Zunahme des diskretisierten Reaktionstern
F
(
u
→
h
(
t
)
)
{\displaystyle F({\vec {u}}_{h}(t))}
räumlich diskretisierten Neumann Randwertproblems für die Diffusion ergibt sich folgendes System der gewöhnlichen Differentialgleichungen (GDGL) für die Reaktionsdiffusionsgleichung:
d
d
t
u
→
h
(
t
)
=
−
A
h
u
→
h
(
t
)
+
F
(
u
→
h
(
t
)
)
{\displaystyle {\frac {d}{dt}}{\vec {u}}_{h}(t)=-A_{h}{\vec {u}}_{h}(t)+F({\vec {u}}_{h}(t))}
mit einem linearen Anteil
−
A
h
u
→
h
(
t
)
{\displaystyle -A_{h}{\vec {u}}_{h}(t)}
F
(
u
→
h
(
t
)
)
{\displaystyle F({\vec {u}}_{h}(t))}
Dieses GDGL System, ergänzt um die Anfangsbedingung gegeben durch eine bekannte Funktion
u
0
(
x
,
y
)
{\displaystyle u^{0}(x,y)}
u
→
(
t
0
)
=
u
→
h
(
t
0
)
=
u
→
0
=
(
u
0
(
x
0
,
y
0
)
,
…
,
u
0
(
x
n
+
1
,
y
m
+
1
)
)
T
{\displaystyle {\vec {u}}(t_{0})={\vec {u}}_{h}(t_{0})={\vec {u}}^{0}=(u^{0}(x_{0},y_{0}),\ldots ,u^{0}(x_{n+1},y_{m+1}))^{T}}
definiert ein Anfangswertproblem für Reaktionsdiffusionsgleichung.
Zeitdiskretisierung der Reaktion-Diffusionsgleichung [ Bearbeiten ] Unter der Zeitdiskretisierung versteht man ein approximatives Vorgehen zur Bestimmung der Lösung eines Anfangswertproblems in
diskreten Zeitpunkten.
Der Zeitintervall
(
t
0
,
T
)
{\displaystyle (t_{0},T)}
(
t
k
,
t
k
+
1
)
{\displaystyle (t_{k},t_{k+1})}
Δ
t
=
t
k
+
1
−
t
k
,
k
=
0
,
1
,
…
K
,
T
=
t
0
+
K
Δ
t
{\displaystyle \Delta t=t_{k+1}-t_{k},\quad k=0,1,\ldots K,\ T=t_{0}+K\Delta t}
Das einfachste numerische Verfahren, das Euler- oder Polygonzugverfahren entsteht durch das Ersetzten der Zeitableitung
d
u
→
h
d
t
{\displaystyle {\frac {d{\vec {u}}_{h}}{dt}}}
Vorwärts- oder Rückwardsdifferenzenquotienten
D
Δ
t
±
u
→
h
(
t
)
=
u
→
h
(
t
±
Δ
t
)
−
u
→
h
(
t
)
Δ
t
≈
d
u
→
h
(
t
)
d
t
{\displaystyle D_{\Delta t}^{\pm }{\vec {u}}_{h}(t)={\frac {{\vec {u}}_{h}(t\pm \Delta t)-{\vec {u}}_{h}(t)}{\Delta t}}\approx {\frac {d{\vec {u}}_{h}(t)}{dt}}}
Dieses Verfahren hat die Konvergenzordnung 1, siehe Approximationsgüte der Differenzenquotienten .
Nach dem Anwenden des ersten Differenzenquotientes im obigen System von GDL ergeben sich folgende Approximationsschemas erster Ordnung:
Unter Verwendung von
D
Δ
t
+
{\displaystyle D_{\Delta t}^{+}}
u
→
h
(
t
k
+
1
)
=
u
→
h
(
t
k
)
+
Δ
t
(
−
A
h
u
→
h
(
t
k
)
+
F
(
u
→
h
(
t
k
)
)
)
,
k
=
0
,
1
,
…
K
,
T
=
t
0
+
K
Δ
t
.
{\displaystyle {\vec {u}}_{h}(t_{k+1})={\vec {u}}_{h}(t_{k})+\Delta t{\Big (}-A_{h}{\vec {u}}_{h}(t_{k})+F({\vec {u}}_{h}(t_{k})){\Big )},\quad k=0,1,\ldots K,\ T=t_{0}+K\Delta t.}
mit dem Startvektor
u
0
(
x
,
y
)
{\displaystyle u^{0}(x,y)}
u
→
h
(
t
0
)
=
u
→
0
=
(
u
0
(
x
0
,
y
0
)
,
…
,
u
0
(
x
n
+
1
,
y
m
+
1
)
)
T
{\displaystyle {\vec {u}}_{h}(t_{0})={\vec {u}}^{0}=(u^{0}(x_{0},y_{0}),\ldots ,u^{0}(x_{n+1},y_{m+1}))^{T}}
Die numerische Lösung in einem neuen Zeitschritt
u
→
h
(
t
k
+
1
)
{\displaystyle {\vec {u}}_{h}(t_{k+1})}
u
→
h
(
t
k
)
{\displaystyle {\vec {u}}_{h}(t_{k})}
Δ
t
{\displaystyle \Delta t}
Δ
t
{\displaystyle \Delta t}
Unter Verwendung von
D
Δ
t
−
{\displaystyle D_{\Delta t}^{-}}
u
→
h
(
t
k
+
1
)
=
u
→
h
(
t
k
)
+
Δ
t
(
−
A
h
u
→
h
(
t
k
+
1
)
+
F
(
u
→
h
(
t
k
+
1
)
)
)
,
k
=
0
,
1
,
…
K
,
T
=
t
0
+
K
Δ
t
.
{\displaystyle {\vec {u}}_{h}(t_{k+1})={\vec {u}}_{h}(t_{k})+\Delta t{\Big (}-A_{h}{\vec {u}}_{h}(t_{k+1})+F({\vec {u}}_{h}(t_{k+1})){\Big )},\quad k=0,1,\ldots K,\ T=t_{0}+K\Delta t.}
mit dem Startvektor
u
0
(
x
,
y
)
{\displaystyle u^{0}(x,y)}
u
→
h
(
t
0
)
=
u
→
0
=
(
u
0
(
x
0
,
y
0
)
,
…
,
u
0
(
x
n
+
1
,
y
m
+
1
)
)
T
{\displaystyle {\vec {u}}_{h}(t_{0})={\vec {u}}^{0}=(u^{0}(x_{0},y_{0}),\ldots ,u^{0}(x_{n+1},y_{m+1}))^{T}}
Die numerische Lösung im neuen Zeitschritt
u
→
h
(
t
k
+
1
)
{\displaystyle {\vec {u}}_{h}(t_{k+1})}
u
→
h
(
t
k
+
1
)
{\displaystyle {\vec {u}}_{h}(t_{k+1})}
Δ
t
{\displaystyle \Delta t}
Δ
t
{\displaystyle \Delta t}
[ Bearbeiten ] Sei eine gewöhnliche Differentialgleichung oder ein System von DGL gegeben allgemein als
y
˙
(
t
)
=
f
(
t
,
y
(
t
)
)
,
y
:
R
→
R
d
,
d
=
1
,
2
,
,
…
.
{\displaystyle {\bf {\dot {y}}}(t)=f(t,{\bf {y}}(t)),\quad {\bf {y}}:{\mathbb {R} }\to {\mathbb {R} }^{d},\ d=1,2,,\ldots .}
Unter Verwendung des zentralen Differenzenquotienten
D
Δ
t
/
2
{\displaystyle D_{\Delta t/2}}
die explizite Mittelpunktregel (verbessertes Eulerverfahren)
y
k
+
1
=
y
k
+
Δ
t
(
f
(
t
k
+
1
/
2
,
y
k
+
1
/
2
)
)
,
y
k
+
1
/
2
=
y
k
+
Δ
t
2
f
(
t
k
,
y
k
)
{\displaystyle {\bf {y}}_{k+1}={\bf {y}}_{k}+\Delta t{\Big (}f(t_{k+1/{2}},{\bf {y}}_{k+1/{2}}){\Big )},\quad {\bf {y}}_{k+1/{2}}={\bf {y}}_{k}+{\frac {\Delta t}{2}}f(t_{k},{\bf {y}}_{k})}
Ein weiteres Verfahren zweiter Ordnung ist die Trapezregel (Newmark scheme) :
y
k
+
1
=
y
k
+
Δ
t
2
(
f
(
t
k
,
y
k
)
+
f
(
t
k
+
1
,
y
k
+
1
)
)
{\displaystyle {\bf {y}}_{k+1}={\bf {y}}_{k}+{\frac {\Delta t}{2}}{\Big (}f(t_{k},{\bf {y}}_{k})+f(t_{k+1},{\bf {y}}_{k+1}){\Big )}}
Runge-Kutta und Mehrschrittverfahren .
Inhomogene Populationsdichte in unserem Beispiel, angepasst von Monitor Einwohnerzahl 2011 In folgender Animation wurde die Reaktionsdiffusiongleichung für kummulierte Infizierte mit explizitem Eulerverfahren auf einem Gebet von 15 x 18 km berechnet.
Animation der Epidemieausbreitung mit geographisch differenzierter Populationsdichte, Anzahl der Gesammtinfizierten pro Rasterzelle (220mx220m), konstanter Diffusionskoeffizient c=0.1, Infektionsrate 0.3. Animation mit konstantem Diffusionskoeffizient
c
=
0.1
{\displaystyle c=0.1}
B
(
x
,
y
)
{\displaystyle B(x,y)}
max
x
∈
D
B
(
x
)
=
800
/
[
k
m
2
]
{\displaystyle \max _{x\in D}B(x)=800/[km^{2}]}
Bevölkerungsdichte Deutschland 2011.
Raumdiskretisierung des regionaldifferenzierten Diffusionskoffizienten [ Bearbeiten ] Um die räumlichen Epidemieausbreitung regional zu differenzieren, nehmen wir an, dass der Diffusionskoeffizient von der Populationsdichte abhängig ist, siehe nicht-konstanter Diffusionkoeffizient
c
(
x
,
y
)
=
c
~
(
B
(
x
,
y
)
)
{\displaystyle c(x,y)={\tilde {c}}(B(x,y))}
Für diesen Fall muss Diffusionsmatrix (das Approximationsschema)
A
h
{\displaystyle A_{h}}
c
/
h
2
{\displaystyle c/h^{2}}
c
(
x
,
y
)
{\displaystyle c(x,y)}
A
h
{\displaystyle A_{h}}
Die homogene Neumann-Randbedingung in diesem Fall lautet:
∂
(
c
u
)
∂
n
→
≡
c
(
x
,
y
)
∇
u
(
x
,
y
)
⋅
n
→
{\displaystyle {\frac {\partial (cu)}{\partial {\vec {n}}}}\equiv c(x,y)\nabla u(x,y)\cdot {\vec {n}}}
Mit Anwendung der einseitigen Differenzenquotienten und der Bezeichnung
c
(
x
i
,
y
j
)
=:
c
i
,
j
{\displaystyle c(x_{i},y_{j})=:c_{i,j}}
am linken und rechten Rand des Rechtecks:
c
0
,
j
u
1
,
j
−
u
0
,
j
h
.
(
−
1
)
=
0
,
c
n
+
1
,
j
u
n
+
1
,
j
−
u
n
,
j
h
.
(
1
)
=
0
,
j
=
0
,
1
,
…
m
+
1
{\displaystyle c_{0,j}{\frac {u_{1,j}-u_{0,j}}{h}}.(-1)=0,\quad c_{n+1,j}{\frac {u_{n+1,j}-u_{n,j}}{h}}.(1)=0,\quad j=0,1,\ldots m+1}
am unteren und oberen Rand des Rechtecks:
c
i
,
0
u
i
,
1
−
u
i
,
0
h
.
(
−
1
)
=
0
,
c
i
,
m
+
1
u
i
,
m
+
1
−
u
i
,
m
h
.
(
1
)
=
0
,
i
=
0
,
1
,
…
n
+
1
{\displaystyle c_{i,0}{\frac {u_{i,1}-u_{i,0}}{h}}.(-1)=0,\quad c_{i,m+1}{\frac {u_{i,m+1}-u_{i,m}}{h}}.(1)=0,\quad i=0,1,\ldots n+1}
Das Approximationsschema für den Diffusionsterm
d
i
v
(
c
(
x
,
y
)
∇
u
(
x
,
y
)
)
=
∂
x
(
c
(
x
,
y
)
∂
x
u
(
x
,
y
)
)
+
∂
y
(
c
(
x
,
y
)
∂
y
u
(
x
,
y
)
)
{\displaystyle div{\Big (}c(x,y)\nabla u(x,y){\Big )}=\partial _{x}{\Big (}c(x,y)\partial _{x}u(x,y){\Big )}+\partial _{y}{\Big (}c(x,y)\partial _{y}u(x,y){\Big )}}
kann mit zweifacher Anwendung des zentralen Differenzenquotienten im obigen Ausdruck
in den inneren Gitterpunkten
(
x
i
,
y
j
)
,
i
=
1
,
…
n
,
j
=
1
,
…
m
{\displaystyle (x_{i},y_{j}),i=1,\ldots n,\ j=1,\ldots m}
d
i
v
(
c
(
x
,
y
)
∇
u
(
x
,
y
)
)
≈
D
h
/
2
,
x
(
c
(
x
i
,
y
j
)
D
h
/
2
,
x
u
(
x
i
,
y
j
)
)
+
D
h
/
2
,
y
(
c
(
x
i
,
y
j
)
D
h
/
2
,
y
u
(
x
i
,
y
j
)
)
{\displaystyle div{\Big (}c(x,y)\nabla u(x,y){\Big )}\approx D_{h/2,x}{\Big (}c(x_{i},y_{j})D_{h/2,x}u(x_{i},y_{j}){\Big )}+D_{h/2,y}{\Big (}c(x_{i},y_{j})D_{h/2,y}u(x_{i},y_{j}){\Big )}}
Herleitung des zweiten Differenzenquotienten bez. x:
D
h
/
2
,
x
(
c
(
x
i
,
y
j
)
D
h
/
2
,
x
u
(
x
i
,
y
j
)
)
=
D
h
/
2
,
x
(
c
i
,
j
u
i
+
1
/
2
,
j
−
u
i
−
1
/
2
,
j
h
)
{\displaystyle D_{h/2,x}{\Big (}c(x_{i},y_{j})D_{h/2,x}u(x_{i},y_{j}){\Big )}=D_{h/2,x}{\Big (}c_{i,j}{\frac {u_{i+1/2,j}-u_{i-1/2,j}}{h}}{\Big )}}
=
1
h
(
c
i
+
1
/
2
,
j
u
i
+
1
,
j
−
c
i
−
1
/
2
,
j
u
i
,
j
h
−
c
i
+
1
/
2
,
j
u
i
,
j
−
c
i
−
1
/
2
,
j
u
i
−
1
,
j
h
)
=
1
h
2
(
u
i
+
1
,
j
c
i
+
1
/
2
,
j
−
u
i
,
j
(
c
i
−
1
/
2
,
j
+
c
i
+
1
/
2
,
j
)
+
u
i
−
1
,
j
c
i
−
1
/
2
,
j
)
{\displaystyle \quad ={\frac {1}{h}}{\Big (}{\frac {c_{i+1/2,j}u_{i+1,j}-c_{i-1/2,j}u_{i,j}}{h}}-{\frac {c_{i+1/2,j}u_{i,j}-c_{i-1/2,j}u_{i-1,j}}{h}}{\Big )}={\frac {1}{h^{2}}}{\Big (}u_{i+1,j}c_{i+1/2,j}-u_{i,j}(c_{i-1/2,j}+c_{i+1/2,j})+u_{i-1,j}c_{i-1/2,j}{\Big )}}
hier bezeichnet
u
i
+
1
/
2
,
j
:=
u
(
x
i
+
h
/
2
)
{\displaystyle u_{i+1/2,j}:=u{\big (}x_{i}+{h}/{2}{\big )}}
(
x
i
,
y
j
)
,
(
x
i
+
1
,
y
j
)
{\displaystyle (x_{i},y_{j}),(x_{i+1},y_{j})}
Analog kann man für den zweiten Differenzenquotienten bez. y zeigen:
D
h
/
2
,
y
(
c
(
x
i
,
y
j
)
D
h
/
2
,
y
u
(
x
i
,
y
j
)
)
=
1
h
2
(
u
i
,
j
+
1
c
i
,
j
+
1
/
2
−
u
i
,
j
(
c
i
,
j
−
1
/
2
+
c
i
,
j
+
1
/
2
)
+
u
i
,
j
−
1
c
i
,
j
−
1
/
2
)
{\displaystyle D_{h/2,y}{\Big (}c(x_{i},y_{j})D_{h/2,y}u(x_{i},y_{j}){\Big )}={\frac {1}{h^{2}}}{\Big (}u_{i,j+1}c_{i,j+1/2}-u_{i,j}(c_{i,j-1/2}+c_{i,j+1/2})+u_{i,j-1}c_{i,j-1/2}{\Big )}}
Insgesamt gilt für den Diffusionsterm:
d
i
v
(
c
(
x
,
y
)
∇
u
(
x
,
y
)
)
≈
1
h
2
(
u
i
+
1
,
j
c
i
+
1
/
2
,
j
+
u
i
,
j
+
1
c
i
,
j
+
1
/
2
−
u
i
,
j
(
c
i
−
1
/
2
,
j
+
c
i
+
1
/
2
,
j
+
c
i
,
j
−
1
/
2
+
c
i
,
j
+
1
/
2
)
+
u
i
−
1
,
j
c
i
−
1
/
2
,
j
+
u
i
,
j
−
1
c
i
,
j
−
1
/
2
)
.
{\displaystyle div{\Big (}c(x,y)\nabla u(x,y){\Big )}\approx {\frac {1}{h^{2}}}{\Big (}u_{i+1,j}c_{i+1/2,j}+u_{i,j+1}c_{i,j+1/2}-u_{i,j}(c_{i-1/2,j}+c_{i+1/2,j}+c_{i,j-1/2}+c_{i,j+1/2})+u_{i-1,j}c_{i-1/2,j}+u_{i,j-1}c_{i,j-1/2}{\Big )}.}
Unter der Anwendung der Approximation der Randbedingungen und des Diffusionsterms erhalten wir folgende Systemmatrix
A
h
=
−
1
h
2
(
−
h
I
0
h
I
0
…
0
I
~
ℓ
,
1
B
1
I
~
r
,
1
⋮
⋮
⋱
⋱
⋱
0
…
h
I
m
+
1
−
h
I
m
+
1
)
,
{\displaystyle A_{h}={\frac {-1}{h^{2}}}{\begin{pmatrix}-hI_{0}&hI_{0}&&\ldots &0\\{\tilde {I}}_{\ell ,1}&B_{1}&{\tilde {I}}_{r,1}&&\vdots \\\vdots &\ddots &\ddots &\ddots &\\0&&\ldots &hI_{m+1}&-hI_{m+1}\end{pmatrix}},}
wobei
I
0
=
d
i
a
g
(
c
→
0
)
,
I
m
+
1
=
d
i
a
g
(
c
→
m
+
1
)
,
c
→
0
=
(
c
0
,
0
,
…
,
c
n
+
1
,
0
)
,
c
→
m
+
1
=
(
c
0
,
m
+
1
,
…
,
c
n
+
1
,
m
+
1
)
,
{\displaystyle I_{0}=diag({\vec {c}}_{0}),\ I_{m+1}=diag({\vec {c}}_{m+1}),\qquad {\vec {c}}_{0}=(c_{0,0},\ldots ,c_{n+1,0}),\quad {\vec {c}}_{m+1}=(c_{0,m+1},\ldots ,c_{n+1,m+1}),}
B
j
=
(
−
h
c
0
,
j
h
c
0
,
j
0
…
0
c
1
/
2
,
j
−
(
c
1
2
,
j
+
c
3
2
,
j
+
c
1
,
j
+
1
2
+
c
1
,
j
−
1
2
)
c
3
/
2
,
j
…
0
⋮
⋱
⋱
⋱
0
…
c
n
−
1
/
2
,
j
−
(
c
n
−
1
2
,
j
+
c
n
+
1
2
,
j
+
c
n
,
j
+
1
2
+
c
n
,
j
−
1
2
)
c
n
+
1
/
2
,
j
0
…
0
h
c
n
+
1
,
j
−
h
c
n
+
1
,
j
)
,
{\displaystyle B_{j}={\begin{pmatrix}-hc_{0,j}&hc_{0,j}&0&\ldots &0\\c_{1/2,j}&-(c_{{\frac {1}{2}},j}+c_{{\frac {3}{2}},j}+c_{1,j+{\frac {1}{2}}}+c_{1,j-{\frac {1}{2}}})&c_{3/2,j}&\ldots &0\\\vdots &\ddots &\ddots &\ddots &\\0&\ldots &c_{n-1/2,j}&-(c_{n-{\frac {1}{2}},j}+c_{n+{\frac {1}{2}},j}+c_{n,j+{\frac {1}{2}}}+c_{n,j-{\frac {1}{2}}})&c_{n+1/2,j}&\\0&\ldots &0&hc_{n+1,j}&-hc_{n+1,j}\end{pmatrix}},}
I
~
ℓ
,
j
=
(
0
…
0
0
c
1
,
j
−
1
2
0
…
0
⋮
⋱
⋱
⋱
⋮
0
…
0
c
n
,
j
−
1
2
0
0
…
0
)
,
I
~
r
,
j
=
(
0
…
0
0
c
1
,
j
+
1
2
0
…
0
⋮
⋱
⋱
⋱
⋮
0
…
0
c
n
,
j
+
1
2
0
0
…
0
)
,
j
=
1
,
…
m
,
I
~
ℓ
/
r
,
j
,
B
j
∈
R
(
n
+
2
)
×
(
n
+
2
)
{\displaystyle {\tilde {I}}_{\ell ,j}={\begin{pmatrix}0&&\ldots &&0\\0&c_{1,j-{\frac {1}{2}}}&0&\ldots &0\\\vdots &\ddots &\ddots &\ddots &\vdots \\0&\ldots &0&c_{n,j-{\frac {1}{2}}}&0\\0&&\ldots &&0\end{pmatrix}},\quad {\tilde {I}}_{r,j}={\begin{pmatrix}0&&\ldots &&0\\0&c_{1,j+{\frac {1}{2}}}&0&\ldots &0\\\vdots &\ddots &\ddots &\ddots &\vdots \\0&\ldots &0&c_{n,j+{\frac {1}{2}}}&0\\0&&\ldots &&0\end{pmatrix}},\quad j=1,\ldots m,\ \quad {\tilde {I}}_{\ell /r,j},B_{j}\in {\mathbb {R} }^{(n+2)\times (n+2)}}
I
0
,
I
m
+
1
=∈
R
(
n
+
2
)
×
(
n
+
2
)
{\displaystyle I_{0},\ I_{m+1}=\in {\mathbb {R} }^{(n+2)\times (n+2)}}
In den obigen Matrizen kann man die Zwischenwerte der Funktion c durch die Mittelwerte ersetzen:
c
i
±
1
2
,
j
≈
1
2
(
c
i
±
1
,
j
+
c
i
,
j
)
,
{\displaystyle c_{i\pm {\frac {1}{2}},j}\approx {\frac {1}{2}}(c_{i\pm 1,j}+c_{i,j}),}
c
i
,
j
±
1
2
≈
1
2
(
c
i
,
j
±
1
+
c
i
,
j
)
.
{\displaystyle c_{i,j\pm {\frac {1}{2}}}\approx {\frac {1}{2}}(c_{i,j\pm 1}+c_{i,j}).}
In diesem Fall braucht man für den raumabhängigen Diffusionsokeffizient nur die Matrix der Werte an den Gitterpunkten
c
i
,
j
{\displaystyle c_{i,j}}
Für stückweise lineare Funktion
c
{\displaystyle c}
c
i
±
1
2
,
j
,
c
i
,
j
±
1
2
{\displaystyle c_{i\pm {\frac {1}{2}},j},\ c_{i,j\pm {\frac {1}{2}}}}
Im Fall einer allgemeinen Funktion ist die Approximation durch die Mittelwerte von zweiter Ordnung, was nach der Addition der
Taylorpolynome für
c
(
x
i
±
h
2
,
y
j
)
,
{\displaystyle c{\Big (}x_{i}\pm {\frac {h}{2}},y_{j}{\Big )},}
c
(
x
i
,
y
j
±
h
2
)
{\displaystyle c{\Big (}x_{i},y_{j}\pm {\frac {h}{2}}{\Big )}}
Dieser Wiki2Reveal Foliensatz Kurs:Räumliche Modellbildung 'Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
↑ M. Hanke Burgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens, Kap. XV , Springer Verlag↑ Natürliche Matrixnormen Wikiversity Artikel zu Matrixnom, abgerufen am 17.06.2020



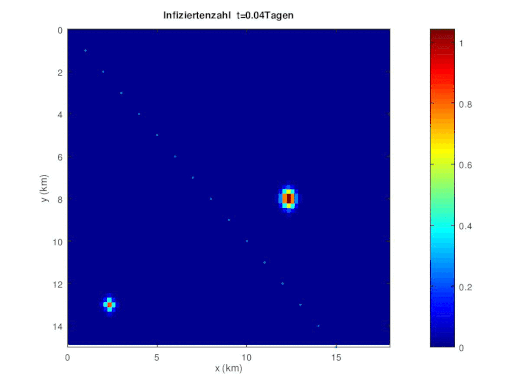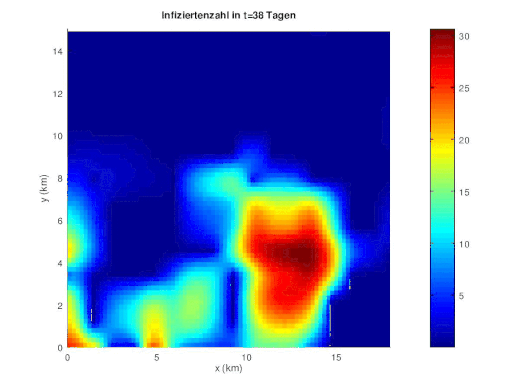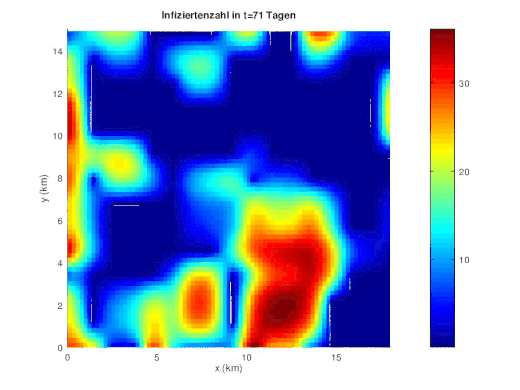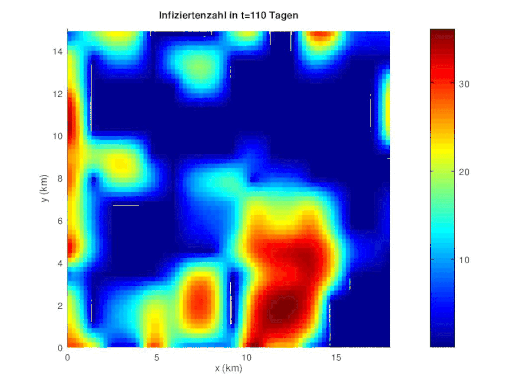


















![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle x,\ x\pm h\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32cf415d7dff0143e3ce9d7f81315a0b9b35f68f)
![{\displaystyle f\in C^{2}[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b220c385bd99fd8dda686821cf269306898af07)
![{\displaystyle x\in [h,b-h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac8bb7733be795bf4f70c67d431ae4fccda63359)

![{\displaystyle C_{1}:=\max _{x\in [a,b]}|f''(x)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b6d4a5addfed1112817b0de210644ee8a68f11e)
![{\displaystyle f\in C^{3}[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ae96d8ea41dcdf22fd790914a0fcd656a514286)

![{\displaystyle C_{2}=\max _{x\in [a,b]}|f'''(x)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35413db962b8e542b42ca404e51b65c718440de2)








![{\displaystyle f\in C^{4}[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f75332ff15579378a353f25337e0cdc6e9df21d)

![{\displaystyle C_{3}:=\max _{x\in [a,b]}|f^{(IV)}(x)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a182b3b1644bbc50eb427d85e104ec343e18ae2)













![{\displaystyle x\in [a,b]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/773c4531c022eddb88d782c0a6ccd2bae7fc18fa)
![{\displaystyle \{x_{i}=a+ih,\ i=1,\ldots ,n\in \mathbb {N} \}\subset [a,b],\quad h={\frac {b-a}{n+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab4c3721e88eb097b68924849616c30ce086c07c)














































![{\displaystyle u:\mathbb {R} ^{2}\to \mathbb {R} ,\ {\bf {x}}=(x,y)\in D:=[a,b]\times [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a87d21f93bf0f4dbb957b71fc78c2be7aa60735)


























![{\displaystyle \partial D,\ D=[a,b]\times [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba76e2c6e707338156fd382821a6458da10a4959)
















![{\displaystyle \ D=[a,b]\times [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f009059a09e4c5cf26ddc29159aad96360f51a4)
























































































![{\displaystyle b\in C^{2}[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d44dccbea206760027a8aa72619f8fc59a853dff)


![{\displaystyle w\in C^{4}[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62c7b98f5cafe3abfd84f422876f97c4e7a2b14b)

![{\displaystyle w\geq 0\ \forall x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1c30948dcfee415f6ef8696e552e4c569e49b12)







![{\displaystyle c\in C[0,1],\ c\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34a9ddfa117508e2cdc8351365a25c6748ca8767)
















![{\displaystyle \||L_{h}^{-1}\||_{\infty }\leq 2\|{\vec {w}}\|_{\infty }\leq 2\max _{x\in [0,1]}|w|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0b99c91339615452b1cb493f8f96ae48d70053e)
![{\displaystyle \max _{x\in [0,1]}|w|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b5599f4439fb90e1c18af80774ec66432f94c22)

![{\displaystyle b\in C^{2}[0,1],\ c\in C[0,1],\ c\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d4409531da6351800aff006f2161fb30811568f)

![{\displaystyle u\in C^{4}[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/873f01af0bc8e81d512598e78cbc902475c97221)

































































![{\displaystyle \max _{x\in D}B(x)=800/[km^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/441ea0daa924e8178f1f6985a39631dc42d4b6bc)



























