Kurs:Mathematische Modellbildung/Lehrerbedarf

Vorwort

In diesem Modell wird aus Gründen der besseren Lesbarkeit das generische Maskulin verwendet. Weibliche und anderweitige Geschlechteridentitäten sind dabei ausdrücklich mit zu verstehen, soweit es für die Aussage erforderlich ist.

Modellierungsproblem

Ziel der Modellierung

Häufig hört man in den Medien, dass es besonders in den sogenannten MINT-Fächern einen Lehrermangel gibt. Darunter fällt auch das Fach Mathematik. Von besonderer Bedeutung ist diese Thematik gerade für Studieninteressierte im Hinblick auf ihre Fächerwahl und die damit verbundenen Einstiegschancen in den Beruf. Aber auch für Bildungspolitiker sind die Zahlen essentiell um durch gezielte Maßnahmen dem Lehrerbedarf gerecht zu werden. Die Modellbildung geht der Frage nach, wie sich der Lehrerbedarf für das Jahr 2026 in Rheinland-Pfalz entwickelt und ob es dann auch genügend Lehrkräfte trotz sinkender Studierendenzahlen gibt. Die Modellbildung berücksichtigt neben verschiedenen Zahlen zu Studierenden auch die Entwicklung der Geburtenrate und Migration, die für Zahl zukünftiger Schülergenerationen entscheidend sind. Weiter werden auch bestehende Zahlen zu Lehrkräften und Personen die aus dem Lehrberuf ausscheiden, in den Blick genommen.

Zielgruppe der Modellbildung

• Sek I: Bildungspolitiker und Studieninteressierte
• Sek II: Bildungspolitiker und Studieninteressierte
• Uni: Bildungspolitiker und Studieninteressierte

Mehrwert der Modellbildung

Der Mehrwert der Modellbildung beläuft sich auf die Sicherung und Planung einer reibungslosen Lehre in der Schule. Sind beispielsweise geburtenstarke Jahrgänge in den kommenden Jahren zu erwarten, so liegt es an den Politikern darauf zu reagieren, indem geeignete Maßnahmen getroffen werden können. Demnach kann gezielte Werbung erfolgen, die Studieninteressierten den Lehramtszweig nahelegt und dafür sorgt, dass der erhöhte Lehrkräftebedarf zeitgerecht gedeckt wird, indem vorzeitig geworben wird um eine gewisse Zahl an Absolventen für einen späteren Zeitpunkt zu garantieren. Werbemaßnahmen könnten eine ansprechende Bezahlung oder eine "Verbeamtungsgarantie" sein. Andere Schritte um dem Schülerwachstum gerecht zu werden, könnten vereinfachte Bedingungen für Quereinsteiger sein, die den Wechsel in den Lehrerberuf erleichtern. Das Einstellen sogenannter PES-Kräfte könnte den Bedarf auch kurzzeitig decken. Letztere Maßnahmen sind eine Erweiterung der Klassengröße oder vermehrte digitale Inhalte in der Lehre.

Wiki2Reveal

• Einführung
• Mathematische Grundlagen
• Implementation
• Modellierungszyklus 1
• Modellierungszyklus 2
• Modellierungszyklus 3
• Bewertung der Modellbildung

Zuordnung zu Nachhaltigkeitszielen

SDG 4: Quality Education

Sustainable Development Goals

Unabdingbar für eine qualitativ hochwertige Bildung sind qualifizierte Lehrkräfte. Dabei ist zu berücksichtigen, dass ausreichend Lehrer vorhanden sein sollten, um Überlastungen und daraus resultierende Einbußen von Unterrichtsqualität zu vermeiden.

Rohdaten

Modellierungszyklus 1

Die Zahl der Studienanfänger für das Fach Mathematik allgemein wurde von dem Statistischen Bundesamt erhoben. Für den ersten Modellierungszyklus sind dabei die Zahlen ab 2017 interessant, da ein Studium in der Regel 5 Jahre dauert und die zukünftigen Absolventen bestimmt werden sollen. Die Zahl der Studienanfänger für das Jahr 2021 wurde bisher noch nicht in die Statistik integriert, weshalb diese Zahl geschätzt werden musste.

Bundesland Rheinland-Pfalz

Jahr	Studienanfänger Mathematik allgemein
2017	616
2018	625
2019	531
2020	500
2021	523

Modellierungszyklus 2

• Die nachfolgende Tabelle enthält Daten aus dem Jahr 2015, allgemein bezogen auf alle Hochschulstudenten ohne Fachbezug . Sie enthält Daten darüber, wie viele Studenten nach dem Studienabschluss im jeweiligen Bundesland bleiben.

Hochschulabsolventen, die nach dem Studium im eigenen Bundesland bleiben

Bundesland	Verbleib von Hochschulabsolventen
Rheinland-Pfalz	54,3%
Hessen	69,9%
Baden-Württemberg	69,3%
Nordrhein-Westfalen	75,1%
Saarland	72,8%

• $12\%$ von den Lehrkräften mit gesundheitlichen Problemen gehen vorzeitig in den Ruhestand.
• Gesamtzahl von $40.471$ Lehrkräften in Rheinland-Pfalz allgemein.
• Rheinland-pfälzische Bevölkerung $4.098.391$ (Stand: 31. Dezember 2020)
• Gesamtbevölkerung Deutschlands $83.129.285$ (Stand: 30. Juni 2021)
• Pensionierte Lehrkräfte in Deutschland $432.520$ (Stand 2019) .

Modellierungszyklus 3

Geburtenzahlen Rheinland-Pfalz

Jahr	Anzahl Geburten
2007	32.536
2008	32.223
2009	30.881
2010	31.574
2011	31.081
2012	31.169
2013	31.989
2014	33.427
2015	34.946
2016	37.518

Migration

Staat	Einwohner(*)	in DE (2018)	in DE (2020)
Ägypten	102.300.000	32.505	37.430
Libyen	6.871.000	14.780	14.900
Tunesien	11.820.000	35.560	38.405
Algerien	43.850.000	18.575	19.160
Marokko	36.910.000	76.200	79.725
Türkei	84.340.000	1.476.410	1.472.390
Syrien	17.500.000	745.645	818.460
Libanon	6.825.000	41.000	41.090

(*) jeweils erstes Ergebnis bei Google Suche "Einwohnerzahl Land"

• Bevölkerungspyramiden der jeweils in der obigen Tabelle behandelten Länder zur Ermittlung der Altersstruktur (Stand 2019)

Modellierungszyklus 1 - Niveau Sekundarstufe I

Der erste Modellierungszyklus ist so aufgebaut, dass Schüler der Sekundarstufe I mit ihrem mathematischen Vorwissen zugreifen können.

Inhaltliche Beschreibung

Die Zahl der neu ausgebildeten Lehrkräfte schwankt jährlich und wird von mehreren Faktoren beeinflusst. Im ersten Modellierungszyklus werden folgende Einflussfaktoren betrachtet:

• Zahl der Studienanfänger
• Abbrecherquote
• Quereinsteiger

Da keine Daten bezüglich der Studienanfänger für das Fach Mathematik auf Lehramt existieren, wird angenommen, dass 60 Prozent der Mathematikstudenten das Fach auf Lehramt studieren. Für ein Lehramtsstudium sind 10 Semester bzw. 5 Jahre vorgesehen. In dem Modell wird davon ausgegangen, dass alle Lehramtsstudierende ihr Studium in Regelstudienzeit abschließen. Die Abbrecherquote im Studienfach Mathematik ist deutlich höher als in anderen Studienfächern und beträgt laut einer Studie circa 40 Prozent . Auch wenn die Abbrecherquote keine feste Größe ist und von Jahr zu Jahr schwankt, wird sie im Folgenden zur Vereinfachung mit 40 Prozent jährlich angenommen. Um einen hohen Lehrerbedarf zu decken und Unterrichtsausfall zu vermeiden, werden Quereinsteiger in den Schuldienst aufgenommen. Während der Anteil der Quereinsteiger in den neuen Bundesländern mit 30 bis 40 Prozent sehr hoch ist, ist er in Rheinland-Pfalz mit einem Prozent sehr gering . Dennoch müssen die Quereinsteiger berücksichtigt werden, da sie zu den neu eingestellten Lehrkräften zählen. In dem Modell werden jährlich 10 Quereinsteiger betrachtet.

Mathematisches Modell

Um eine Aussage über die neu ausgebildeten Mathematiklehrkräfte in Rheinland-Pfalz zu treffen, genügen einfache Rechenoperationen, über die die Schüler der Sekundarstufe I verfügen.

Zahl der Studienanfänger

Die Zahl der Studienanfänger für das Fach Mathematik auf Lehramt wird mithilfe einer Prozentrechnung bestimmt. Dabei entspricht die Zahl der Studienanfänger für das Fach Mathematik allgemein dem Grundwert (G). Der Prozentsatz ist, wie in der inhaltlichen Beschreibung erläutert, mit 60% gegeben. Der gesuchte Prozentwert (W), das heißt die Zahl der Studienanfänger für das Fach Mathematik auf Lehramt, lässt sich mit der folgenden Formel ermitteln: $W=0,6\cdot G$

Der Prozentwert W kann bei dieser Rechnung auch eine Dezimalzahl darstellen. Die Zahl der Studienanfänger für das Fach Mathematik auf Lehramt muss jedoch zwingend eine natürliche Zahl sein, da nur ganze Personen gezählt werden können. Folglich muss das Ergebnis gerundet werden. Zeigt die erste Nachkommastelle eine der Zahlen 0, 1, 2, 3 oder 4, so wird abgerundet. Bei den Zahlen 5, 6, 7, 8 oder 9 wird aufgerundet.

Beispiel: Im Jahr 2017 haben 616 Personen angefangen, Mathematik zu studieren. Die Zahl der Lehramtsstudenten beträgt 370, da $0,6\cdot 616=369,6$.

Es ergeben sich die folgenden Werte:

Bundesland Rheinland-Pfalz

Jahr	Studienanfänger Mathematik allgemein	Studienanfänger Mathematik Lehramt
2017	616	370
2018	625	375
2019	531	319
2020	500	300
2021	523	314

Zahl der Absolventen

Die Zahl der Absolventen eines Jahres kann aus der Zahl der Studienanfänger fünf Jahre zuvor unter Berücksichtigung der Abbrecherquote von 40 Prozent ermittelt werden. Das mathematische Werkzeug hierzu ist wieder die Prozentrechnung. Der Prozentsatz für die Rechnung beträgt jedoch nicht 40 Prozent, sondern 60 Prozent, da man die Absolventen und nicht die Abbrecher bestimmen möchte. Der Grundwert (G) entspricht der Zahl der Studienanfänger für das Fach Mathematik auf Lehramt fünf Jahre zuvor. Die Zahl der Absolventen (Prozentwert W) wird nun mit $W=0,6\cdot G$ berechnet.

Auch hier muss analog zur ersten Rechnung gerundet werden.

Beispiel: Im Jahr 2022 werden 222 Lehramtsstudenten mit dem Fach Mathematik ihr Studium abschließen, da im Jahr 2017 370 mit ihrem Studium begonnen haben und $0,6\cdot 370=222$.

Es ergeben sich die folgenden Werte:

Bundesland Rheinland-Pfalz

Jahr	Studienanfänger Mathematik allgemein	Studienanfänger Mathematik Lehramt	Absolventen
2017	616	370
2018	625	375
2019	531	319
2020	500	300
2021	523	314
2022			222
2023			225
2024			191
2025			180
2026			188

Zahl der neu ausgebildeten Lehrkräfte

Die Zahl der neu ausgebildeten Lehrkräfte berechnet sich nun aus der Summe der Absolventen und der Quereinsteiger. Im Jahr 2026 sind 198 neue Lehrkräfte ausgebildet worden, da $188+10=198$.

Bundesland Rheinland-Pfalz

Jahr	Studienanfänger Mathematik allgemein	Studienanfänger Mathematik Lehramt	Absolventen	neu ausgebildete Lehrkräfte
2017	616	370
2018	625	375
2019	531	319
2020	500	300
2021	523	314
2022			222	232
2023			225	235
2024			191	201
2025			180	190
2026			188	198

Software

Tabellenkalkulation

Die Rechnungen, die im mathematischen Modell beschrieben wurden, lassen sich auch in ein Tabellenkalkulationsprogramm implementieren. Für diesen Zyklus wurde Microsoft Excel verwendet. Neben Excel kann auch das Open Source Programm LibreOffice Calc benutzt werden. Mithilfe der Software erhält man die Daten effizienter als mit der Hand oder dem klassischen Taschenrechner.

Implementation in Excel

• Um die Zahl der Studienanfänger für das Fach Mathematik auf Lehramt im Jahr 2017 zu bestimmen, wird der folgende Befehl verwendet:

=RUNDEN(B2*0,6;0)

• Um die Zahl der Absolventen des Jahres 2022 zu ermitteln, wird der folgende Befehl verwendet:

=RUNDEN(C2*0,6;0)

• Nachdem die Zahl der Absolventen bestimmt wurde, müssen nun noch die Quereinsteiger addiert werden. Für die Zahl der neu ausgebildeten Lehrkräfte im Jahr 2022 ergibt sich daher der folgende Befehl:

=D7+10

Die weiteren Jahre folgen jeweils analog.

Geogebra

Zur Visualisierung der errechneten Werte wird die dynamische Geometrie Software GeoGebra verwendet. Zunächst werden die Zahlen der Studienanfänger für das Fach Mathematik auf Lehramt in GeoGebra übertragen. Mithilfe des Tools „Analyse zweier Variablen“ und einem Regressionsmodell wird eine Sinusfunktion interpoliert.

Im Gegensatz zu einer Polynomfunktion oszilliert der Sinus zwischen einer oberen und unteren Schranke. Die Polynomfunktion hingegen würde keine sinnvolle Schranke erreichen. Daher die Sinusfunktion.

Die entstandene Funktionsgleichung lautet:

$f(x)=41.9239\cdot sin(1.1956\cdot x+2.1237)+336.1706$

Anmerkung: Die Herleitung dieser Gleichung sollte nicht mit den Schülerinnen und Schülern besprochen werden. Für den Unterricht sind lediglich die Anwendungen relevant.

Die Funktion $f$ ist in der Grafik in grün abgebildet. Die Punkte $P_{1},...,P_{5}$ geben die Zahlen der Studienanfänger für das Fach Mathematik auf Lehramt in Abhängigkeit von der Zeit an. Die $x$-Werte beschreiben somit das jeweilige Jahr und die $y$-Werte die Zahl der Studienanfänger.

Beispiel: $P_{5}$ sagt aus, dass es im Jahr 2021 314 Studienanfänger für das Fach Mathematik auf Lehramt gibt.

Die Punkte liegen nicht direkt auf dem Graphen von $f$. Daher werden neue Punkte $A,...,E$ erstellt, die dieselben $x$-Werte wie die Punkte $P_{1},...,P_{5}$ haben, aber auf dem Graphen von $f$ liegen. Dadurch verändern sich die $y$-Werte geringfügig. Diese Änderung ist jedoch im Hinblick auf das Ziel der Modellierung vertretbar.

Implementation der Studienanfänger in GeoGebra

Damit der Graph der Funktion gestaucht und verschoben werden kann, müssen Parameter in die Funktionsgleichung eingefügt werden. Die neu entstandene Funktion $g$ besitzt also die Funktionsgleichung:

$g(x)=a\cdot (41.9239\cdot sin(1.1956\cdot (x-c)+2.1237)+336.1706)+b$

Die Funktion $g$ ist in blau dargestellt. Zunächst wird der Parameter $a$ betrachtet. Dieser sorgt für eine Streckung bzw. Stauchung in $y$-Richtung. In dem Modell wird $a=0,6$ gesetzt, da eine Abbrecherquote von 40 Prozent vorliegt und somit 60 Prozent ihr Studium erfolgreich abschließen werden.

Implementation der Abbrecherquote in GeoGebra

Da das Studium 5 Jahre dauert, sind die Studienanfänger eines Jahres $t$ die Absolventen des Jahres $t+5$. Folglich muss der Graph von $g$ um fünf Jahre nach rechts verschoben werden. Dies wird durch den Parameter $c$ erreicht.

Implementation der Absolventen in GeoGebra

Abschließend müssen noch die Quereinsteiger zu den Absolventen addiert werden, wodurch eine Verschiebung des Graphen von $g$ in $y$-Richtung hervorgerufen wird. Die Anzahl der Quereinsteiger lässt sich mit dem Parameter $b$ steuern.

Die Punkte $A_{1},...,E_{1}$ stellen nun die neu verfügbaren Lehrkräfte dar.

Implementation der Quereinsteiger in GeoGebra

Resultate der Modellierung

Zyklus 1 beantwortet die Frage nach der Anzahl der neu ausgebildeten Mathematiklehrkräfte in Rheinland-Pfalz. Im Jahr 2026 können potenziell 198 neue Lehrkräfte eingestellt werden.

Bundesland Rheinland-Pfalz

Jahr	neu ausgebildete Lehrkräfte
2022	232
2023	235
2024	201
2025	190
2026	198

Bewertung und Optimierung

Bewertung

• Excel: numerisch genau
• GeoGebra: gute Visualisierung, Einsatz von Parametern

Verfügt man über die Zahl der Studienanfänger, so kann man unter Berücksichtigung der Abbrecherquote und den Quereinsteigern eine Aussage über die neu ausgebildeten Lehrkräfte in fünf Jahren treffen.

Modellkritik und Optimierung

• Anteil der Lehramtsstudenten von 60% an allen Mathematikstudenten wird angenommen
• Annahme Einhaltung der Regelstudienzeit trifft nicht immer zu
• Abbrecherquote und Quereinsteigerzahl werden zur Vereinfachung als konstant angenommen
• Referendariat nicht berücksichtigt
• Kleinere Rundungsfehler vorhanden, aber für Ergebnis nicht relevant
• Punkte dürfen eigentlich nicht verbunden werden (diskrete Werte)

• Annahme: Alle Absolventen bleiben nach dem Studium in Rheinland-Pfalz
• Aktuelle Anzahl an Lehrkräften im Dienst sowie Schülerzahlen nicht berücksichtigt

Modellierungszyklus 2 - Niveau Sekundarstufe II

Der zweite Modellierungszyklus ist so aufgebaut, dass Schüler der Sekundarstufe II mit ihrem mathematischen Vorwissen zugreifen können.

Um die Frage zu beantworten, ob für das Jahr 2026 ein Bedarf an Lehrern in der Sekundarstufe I im Fach Mathematik besteht, müssen weitere Indikatoren herangezogen werden. Einfluss auf den Lehrerbedarf haben unter anderem

• die Anzahl neu ausgebildeter Lehrkräfte (siehe Daten Zyklus 1): Hierbei berücksichtigen wir neu in diesem Zyklus, dass diese ebenfalls abwandern können, beispielsweise in benachbarte Bundesländer von Rheinland-Pfalz
• Lehrkräfte, die aus dem Schuldienst ausscheiden, etwa aus gesundheitlichen Gründen oder weil sie das Pensionsalter erreicht haben.

Teil 1: Wanderungsverhalten Absolventen

Inhaltliche Beschreibung

Nicht alle Studierende bleiben nach Abschluss ihres Lehramtsstudiums dem jeweiligen Bundesland erhalten. Einige von ihnen beschließen vor Antritt ihrer Stelle noch zu verreisen und wiederum andere wechseln aufgrund besserer Berufschancen, wie etwa der Verbeamtung, das Bundesland. Damit die Übergangsmatrix eine überschaubare Dimension hat, wurden die Wanderungsziele eingeschränkt. Naheliegend ist es hierbei, das Wanderungsverhalten zwischen Rheinland-Pfalz und seinen Nachbarbundesländer zu betrachten.

Folgende Bundesländer grenzen an Rheinland-Pfalz (RP):

• Hessen (H)
• Baden-Württemberg (BW)
• Nordrhein-Westfalen (NW)
• Saarland (S)

Die nachfolgende Tabelle enthält Daten aus dem Jahr 2015, allgemein bezogen auf alle Hochschulstudenten ohne Fachbezug . Diese Daten werden für das Modell genutzt, um annäherungsweise korrekte und realistische Daten für das Jahr 2026 zu generieren. Sie enthält Daten darüber, wie viele Studenten nach dem Studienabschluss in dem Bundesland bleiben.

Hochschulabsolventen, die nach dem Studium im eigenen Bundesland bleiben

Bundesland	Verbleib von Hochschulabsolventen
Rheinland-Pfalz	54,3%
Hessen	69,9%
Baden-Württemberg	69,3%
Nordrhein-Westfalen	75,1%
Saarland	72,8%

Mathematisches Modell

Mithilfe der realen Daten aus der obigen Tabelle über den Verbleib von Absolventen und weiteren geschätzten Anteilen, können die Werte der Wanderungsbewegungen angenähert werden. Die nachfolgende Skizze visualisiert die jeweiligen Bewegungen von Bundesland zu Bundesland. Die Abkürzung "SO" steht dabei für Sonstige, also die übrigen Bundesländer, welche nicht an Rheinland-Pfalz angrenzen.

Skizze Wanderungsverhalten von Absolventen

Im folgenden kann die Skizze in eine Tabelle umgewandelt werden, deren Einträge später in eine Übergangsmatrix überführt werden können. Die Tabelle wird so gelesen, dass in den Spalten die Bundesländer stehen, aus denen die Absolventen wegziehen und in den Zeilen die Bundesländer stehen, in die die Absolventen wandern. Also von wo nach wo eine Wanderung stattfindet.

Beispiel: Von Rheinland-Pfalz nach Nordrhein-Westfalen wandern 7,7% der Absolventen.

Wanderungsverhalten zwischen Rheinland-Pfalz und seinen Nachbarbundesländern

Bundesland	RP	H	BW	NW	S	SO
RP	54,3%	1,9%	4,8%	3,5%	9,6%	0,3%
H	9,1%	69,9%	6,5%	3,3%	2,7%	1,5%
BW	14,6%	6,5%	69,3%	1,6%	3,2%	2,2%
NW	7,7%	4,4%	3,1%	75,1%	2,5%	0,9%
S	2,1%	0,2%	0,1%	0,1%	72,8%	0%
SO	12,2%	17,1%	16,2%	16,4%	9,2%	92,7%

Der prozentuale Anteil der Absolventen aus den sonstigen Bundesländern, die in das Saarland wandern liegt nahe 0 und wird zur Vereinfachung mit 0 angenommen. Anschließend kann die Tabelle in eine Matrix, die Übergangsmatrix $W$ überführt werden. Die Matrix liest sich dann ebenfalls so wie die Tabelle. Dabei sind Prozentangaben in Dezimalzahlen umzuwandeln.

Zusammensetzung der Übergangsmatrix $W$

Um nun eine Vorhersage über die Anzahl an Absolventen nach einem Wanderungszyklus zu treffen, muss die entstandene Übergangsmatrix $W$ mit einem Vektor $A$ multipliziert werden. Dieser Vektor gibt die aktuellen Absolventenzahlen plus Quereinsteiger (im Jahr 2022) vor der Wanderung an. Der erste Eintrag des Vektors von 232 versteht sich dabei als Ergebnis des ersten Zyklus.

Zusammensetzung Vektor $A$

Veranschaulichung der Implementierung der Daten in Maxima

Das Ergebnis der Multiplikation der Übergangsmatrix $W$ der Wanderungsbewegungen mit dem Vektor $A$ der Anzahl der Absolventen wird dabei wieder als Vektor verstanden, der die Anzahl der Absolventen nach ihrer Wanderung angibt.

Der entstandene Vektor beinhaltet die Absolventen- und Quereinsteigerzahlen aus dem Jahr 2022 entsprechend für die jeweiligen Bundesländer. Die obige Rechnung wird nun weitere vier mal durchgeführt, die erste Zeile der Vektoren (Wert für RLP) wird für die Jahre 2023, 2024, 2025 und 2026 mithilfe der entsprechenden Ergebnisse aus Zyklus 1 angepasst. Aufgrund unzureichender Daten werden die Zahlen der Absolventen und Quereinsteigern in den anderen Bundesländern für alle fünf Jahrgänge verwendet.

Nach jeweils fünf Berechnungen mit Hilfe von Maxima erhält man folgende Ergebnisse. Dabei ist anzumerken, dass aus den entsprechenden Vektoren jeweils nur die erste Zeile betrachtet wurde, da uns nur die Zahlen für Rheinland-Pfalz in unserem Modell interessieren.

Absolventen/Quereinsteiger, die ihren Dienst in Rheinland-Pfalz antreten

	Anzahl Lehrkräfte
2022	201
2023	203
2024	184
2025	178
2026	183

Teil 2: Wanderungsverhalten im Dienstverhältnis

Inhaltliche Beschreibung

Zur Ermittlung des Lehrerbedarfs zu einem gewissen Zeitpunkt ist es ebenfalls notwendig, die Zahl an Ausscheidungen aus diesem Beruf zu berücksichtigen. Ein Grund für die Ausscheidung kann neben dem Eintreten in den Ruhestand auch der Wechsel des Berufszweiges sein. Nicht zu vernachlässigen ist auch die Zahl derer, die aufgrund von gesundheitlichen Problemen zum Pausieren oder Ausscheiden gezwungen sind. Als eine häufige "Lehrerkrankheit" ist hier der Burn-Out zu nennen. [Eine Schwangerschaft und der damit verbundene Dienstausfall wird in diesem Modell unter gesundheitlichen Problemen eingeordnet.]

Mathematisches Modell

Zur Berechnung der im Dienstverhältnis stehenden Lehrkräfte werden folgende fiktive Werte für die Wanderung angenommen. Beispielsweise nehmen von den schon pensionierten Lehrkräften (in diesem Modell "in Rente" genannt) $0,9\%$ wieder den Dienst auf während $12\%$ von den Lehrkräften mit gesundheitlichen Problemen in den vorzeitigen Ruhestand gehen.

Die $2,5\%$ der Lehrkräfte im Dienst, die innerhalb eines Jahres pensioniert werden, entsprechen dabei ${\frac {1}{40}}$ aller Lehrkräfte. Die Annahme folgt aus der Theorie, dass es insgesamt 40 Dienstjahre gibt, wovon jedes Jahr ein Dienstjahrgang ausscheidet und ein neuer hinzukommt.

Daraus ergeben sich Skizze und Tabelle (analog zu Teil 1) wie folgt:

Skizze Dienstverhältnis

Wanderungsverhalten im Dienstverhältnis

	Rente	Im Dienst	Gesundheitliche Probleme
Rente	99,1%	2,5%	12%
Im Dienst	0,9%	94,5%	28%
Gesundheitliche Probleme	0%	3%	60%

Die Daten aus der Tabelle bilden die Übergangsmatrix $D$. Um die Anzahl der aktuellen Mathelehrer in Rheinland-Pfalz im Jahr 2021 zu bestimmen wird angenommen, dass diese einen Anteil von $20\%$ an der Gesamtlehrerzahl von 40.471 ausmachen.

(Die 20% resultieren aus den Ergebnissen von Zyklus 1: Jährlich beginnen circa 200 neue Mathelehrer ihren Dienst. Wenn man davon ausgeht, dass man 40 Jahre in diesem Beruf arbeitet, ergeben sich $200\cdot 40=8000$ Mathelehrkräfte insgesamt. $8000$ von etwa $40.000$ Lehrern entspricht einem Anteil von $20\%$ (${\frac {8000}{40.000}}=0,2$). Zudem ergeben stichprobenartigen Überprüfungen von verschiedenen Schulbelegschaften auch etwa ein Prozentsatz von $20\%$ Mathelehrkräften.)

Somit ergeben sich $0,2\cdot 40.471=8094,2\approx 8094\in \mathbb {N}$ Mathelehrkräfte im Dienst für Rheinland-Pfalz.

Auf Grundlage von Daten aus dem Jahr 2019 für ganz Deutschland wird die Zahl der pensionierten Lehrkräfte berechnet. Im ersten Schritt betrachtet man, wie viel Prozent die rheinland-pfälzische Bevölkerung von der gesamten Deutschen Bevölkerung ausmacht: ${\frac {4.098.391}{83.129.285}}\approx 0.0493$, das sind etwa $4,93\%$.

Stand 2019 sind 432.520 Lehrkräfte in Deutschland pensioniert . Auf Rheinland-Pfalz bezogen ergeben sich dann ${432.520\cdot 0,0493}=21.323,236\approx 21.323\in \mathbb {N}$ pensionierte Lehrkräfte.

Da eine Verbeamtung früher üblich war, gehen wir davon aus, dass alle Lehrkräfte in Pension sind und vernachlässigen diejenigen Lehrer, die ohne Beamtenstatus in dem Beruf gearbeitet haben.

Spezifisch erhält man

$0,2\cdot 21.323=4264,6\approx 4265\in \mathbb {N}$ pensionierte Mathematiklehrkräfte in Rheinland-Pfalz.

Die Zahl der Mathelehrer, die aktuell aus gesundheitlichen Gründen dienstunfähig sind, wurde aufgrund fehlender Datengrundlage mit 6,6% geschätzt:

$0,066\cdot 8094=534,204\approx 534\in \mathbb {N}$

Somit ergibt sich $X$= ${\begin{pmatrix}4265\\8094\\534\end{pmatrix}}$

Veranschaulichung der Implementierung in Maxima

Bei obiger Rechnung wird analog zu Teil 1 die Übergangsmatrix $D$ mit dem Vektor $X$ multipliziert. Dieser Vektor gibt dabei die Gesamtzahlen an pensionierten Lehrkräften, Lehrern im Dienst und Lehrern, die aufgrund gesundheitlicher Probleme pausieren, an (speziell für Mathematik in Rheinland-Pfalz). Nach der Multiplikation erhält man die entsprechenden Werte für ein Jahr später. Da nicht nur Lehrer aus dem Dienst ausscheiden, werden im nächsten Schritt die neu eingestellten Lehrkräfte aus Teil 1 miteinbezogen und hinzu addiert. Um Dezimalstellen zu vermeiden wird das Ergebnis zum Schluss noch gerundet, da die Lehreranzahl nur sinnvoll mit Zahlen aus $\mathbb {N}$ angegeben werden kann. Die eben beschriebene Rechnung wird insgesamt fünf Mal (auf dem Bild sind die ersten zwei abgebildet) durchgeführt, jeweils für 2022, 2023, 2024, 2025 und 2026, wobei der Startvektor die Zahlen aus dem Vorjahr enthält.

Software

Zur Implementation des zweiten Zyklus wird das Open Source Computeralgebrasystem Maxima verwendet. Genauer wird die graphische Benutzeroberfläche wxMaxima genutzt. wxMaxima bietet neben vielen Funktionalitäten wie der Manipulation algebraischer Ausdrücke, Bestimmung von Grenzwerten, Lösung von Gleichungen oder der Berechnung von Matrizen eine benutzerfreundliche Oberfläche und einfache Bedienung. Bei Zyklus 2 steht das Rechnen mit Matrizen im Vordergrund. Wichtig bei der Nutzung von Maxima ist allgemein, dass bei der Eingabe von Dezimalzahlen anstatt Kommata Punkte eingegeben werden müssen

• Matrizen eingeben

1. Variante

Über "Algebra" auf "Matrix eingeben" klicken

Zeilen- und Spaltenanzahl der Matrix eingeben und diese benennen

Entsprechende Werte in die Matrix eintragen

2.Variante

Direkte Eingabe: Matrix wird zeilenweise eingegeben

matrix([0.991,0.025,0.12],[0.009,0.945,0.28],[0,0.03,0.6])

Eingabe mit der Tastenkombination Shift & Return abschließen

• Matrizenmultiplikation

Befehl zur Matrizenmultiplikation

• Addition zweier Matrizen

Befehl zur Addition zweier Matrizen/Zahlen

• Runden

Befehl zum Runden (eines Vektors)

Resultate der Modellierung

Zyklus 2 Teil 1 beantwortet die Frage, wie viele Absolventen den Dienst in Rheinland-Pfalz tatsächlich antreten mit Berücksichtigung der Ab- und Zuwanderung in andere Bundesländer.

Absolventen/Quereinsteiger, die ihren Dienst in Rheinland-Pfalz antreten

	Anzahl Lehrkräfte
2022	201
2023	203
2024	184
2025	178
2026	183

Zyklus 2 Teil 2 beantwortet die Frage, wie viele Lehrkräfte in einem bestimmten Jahr im Dienst sind unter Berücksichtigung derer, die in Rente gehen oder aufgrund von gesundheitlichen Problemen zeitweilig dem Dienst fern bleiben (müssen) und den Lehrkräften, die neu in den Dienst eintreten.

Mathematiklehrer im Dienst

	Neues Jahr	Vorjahr	Differenz
2022	8038	8094	-56
2023	7997	8038	-41
2024	7946	7997	-51
2025	7896	7946	-50
2026	7857	7896	-39

Bewertung und Optimierung

Aufgrund fehlender Daten mussten an einigen Stellen Werte geschätzt werden, somit bilden diese nicht exakt die Realität ab. Für eine bessere Übersicht wurden folgende Aspekte vernachlässigt:

• Auslandswanderung (Bezug des Wanderungsverhaltens nur auf Deutschland)
• Wechsel von Lehrkräften in ein anderes Berufsfeld
• Untergliederung in Gymnasium, Integrierte Gesamtschule und Realschule-Plus
• Sterben von pensionierten Mathematiklehrkräften

• Annahme: Anzahl angehender Lehrkräfte außerhalb RLP bleiben konstant
• Schwankungen bei der Zahl von pensionierten Lehrern, die wieder zurückkehren ist situationsbedingt
• Zahl der Rentner, die gesundheitliche Probleme als Verbindung in der Realität nicht bekannt

Ob nun aufgrund der sinkenden Lehrerzahlen ein erhöhter Bedarf besteht, kann zum jetzigen Zeitpunkt noch nicht beurteilt werden, da zu einer genaueren Aussage noch die entsprechenden Schülerzahlen fehlen. Jedoch ist der Trend erkennbar, dass die Zahl der Lehrkräfte im Dienst kontinuierlich abnimmt und so die Vermutung nahe liegt, das Lehrkräfte fehlen werden. Genauer wird das nochmal in Zyklus 3 untersucht.

Modellierungszyklus 3 - Niveau Uni

Der dritte Modellierungszyklus ist so aufgebaut, dass Studenten der Hochschule mit ihrem mathematischen Vorwissen zugreifen können. Auf der Basis ihrer Kenntnisse und Fähigkeiten sollen Handlungsempfehlungen für Bildungspolitiker aufgestellt werden, um den Lehrerbedarf zu steuern.

Nachdem in Modellierungszyklus 2 die Zahl der Lehrkräfte 2026 ermittelt wurde, müssen nun noch die Schülerzahlen für das Jahr 2026 bestimmt werden, um eine konkrete Aussage über den Lehrerbedarf treffen zu können. Dabei fokussiert sich das Modell auf die Schülerzahlen in der Sekundarstufe 1 in Rheinland-Pfalz.

Inhaltliche Beschreibung

Es wird angenommen, dass die Schüler in der Sekundarstufe zwischen 10 und 15 Jahren alt sind. Die Schülerzahl 2026 setzt sich daher aus den folgenden Punkten zusammen:

• Geburtenzahlen von 2011-2016 in Rheinland-Pfalz
• Kinder im Alter von 10 bis 15 Jahren, die zwischen 2020 und 2026 nach Rheinland-Pfalz wandern werden
• Kinder im Alter von 4 bis 9 Jahren, die bis 2020 nach Rheinland-Pfalz gewandert sind

Bei der Migration werden die nordafrikanischen Länder Ägypten, Libyen, Tunesien, Algerien und Marokko betrachtet. Die klimatischen Veränderungen können Menschen in diesen Ländern dazu zwingen, ihre Heimat zu verlassen. Aufgrund der geographischen Lage ist eine Migration nach Europa sehr wahrscheinlich. Deutschland ist als Zielland bei den Migranten sehr beliebt. Neben den nordafrikanischen Ländern, werden drei weitere Länder betrachtet, die ebenfalls am Mittelmeer liegen. Diese sind Syrien, Libanon und die Türkei. Aus der Türkei und Syrien waren die Migrantenströme in der Vergangenheit bereits hoch.

Mathematisches Modell

Geburtenzahlen 2011-2016

Mithilfe der Geburtenzahlen von 2011 bis 2016 lässt sich die Anzahl der Einschulungen in den Jahren 2021 bis 2026 bestimmen. Da in Deutschland bzw. Rheinland-Pfalz eine Schulpflicht besteht, werden alle Kinder (bis auf sehr wenige Ausnahmen, die zu vernachlässigen sind) in die 5.Klasse eingeschult. In der Regel sind die Schüler in der 5.Klasse 10 Jahre alt, sodass beispielsweise die Zahl der Geburten im Jahr 2012 der Zahl der Einschulungen in die weiterführende Schule im Jahr 2022 entspricht. Auch wenn die Kindersterblichkeit mit 0,4% in Deutschland sehr gering ist, wird sie dennoch im Modell betrachtet, um die Zahlen so realistisch wie möglich zu halten. Für Rheinland-Pfalz gibt es keine Daten über die Kindersterblichkeit. Jedoch sind die 0,4% auch in Rheinland-Pfalz annehmbar.

Die Zahl der Einschulungen in einem Jahr $t$ ergibt sich also aus der Zahl der Geburten im Jahr $t-10$ mal 0,996. Da eine Personenanzahl nur einer Natürlichen Zahl entsprechen kann, muss sinnvoll gerundet werden. Beispiel: Im Jahr 2022 werden 31.044 Schüler in die 5.Klasse eingeschult, da $31.169\cdot 0,996=31.044,324$.

Bundesland Rheinland-Pfalz

Jahr	Anzahl Geburten	Jahr	Anzahl Einschulungen 5.Klasse
2011	31.081	2021	30.957
2012	31.169	2022	31.044
2013	31.989	2023	31.861
2014	33.427	2024	33.293
2015	34.946	2025	34.806
2016	37.518	2026	37.368
$\sum$	200.130	$\sum$	199.329

Migration zwischen 2020 und 2026

Neben den in Rheinland-Pfalz geborenen Kinder werden im Jahr 2026 auch Kinder in der Sekundarstufe 1 sein, die erst noch nach Rheinland-Pfalz wandern werden. Um die Zahl dieser Kinder zu ermitteln, wird zunächst die Zahl der Migranten in Rheinland-Pfalz in den Jahren 2018 und 2020 betrachtet. Da diese Daten nicht vorliegen, werden sie mithilfe der Zahl der Migranten in Deutschland berechnet. Laut einer Studie leben 5 Prozent der in Deutschland erfassten Migranten in Rheinland-Pfalz . Somit wird die Zahl der Migranten, die in Deutschland leben, mal 0,05 genommen.

Implementation der Migranten 2018 & 2020 in Excel

Mithilfe der linearen Regression als Werkzeug könnten die ermittelten Wertepaare approximiert werden. Unter Berücksichtigung der Werte von 2018 bis 2020 ergibt sich die Funktionsvorschrift: $f(x)=-3.959.252,835+2022,5\cdot x$

Dieser Ansatz kann verworfen werden, da lineare Funktionen nicht konvergieren und somit gegen keine Sättigungsgrenze steuern. In der Realität erreicht die Migration aber eine obere Schranke, da nicht mehr Menschen aus einem Land auswandern können, als das Land Einwohner hat.

Stattdessen wird zunächst ein exponentieller Anstieg der Migrantenzahlen erwartet, die dann in ein beschränktes Wachstum übergehen. Dieser Zusammenhang kann mit dem logistischen Wachstum beschrieben werden. Die Formel für das logistische Wachstum lautet:

$f(t)={\frac {f(0)\cdot S}{f(0)+(S-f(0))\cdot e^{-S\cdot k\cdot t}}}$

Das Jahr 2018 entspricht $t=0$. Aus der Tabelle lässt sich ablesen, dass im Jahr 2018 122.034 Migranten in Deutschland lebten. Daher gilt:

$f(0)=122.034$

Nun muss die Sättigungsgrenze S ermittelt werden, das heißt wie viele Menschen maximal nach Rheinland-Pfalz wandern können. Dafür wird zunächst die Summe der Einwohner in den Herkunftsländern betrachtet. Diese beträgt 310.416.000 Menschen. Mit der Annahme, dass höchstens 20% nach Deutschland wandern, beträgt die Sättigungsgrenze S für Deutschland 62.083.200 Personen. Wie zuvor bereits beschrieben leben 5% der in Deutschland erfassten Migranten in Rheinland-Pfalz, sodass die Sättigungsgrenze S für Rheinland-Pfalz bei 3.104.160 liegt. Zusammengefasst gilt:

$S=310.416.000\cdot 0,2\cdot 0,05=3.104.160$

Um die Wachstumskonstante $k$ zu bestimmen, wird ein weiteres Wertepaar benötigt. Aus der Tabelle lässt sich entnehmen, dass 2020 126.079 Migranten in Deutschland lebten. Das Jahr 2020 entspricht $t=2$. Es gilt:

$f(2)=126.079$

Dieses Wertepaar wird nun zusammen mit $f(0)$ und $S$ in die Formel für das logistische Wachstum eingesetzt. Die Gleichung wird nach k aufgelöst.

$f(2)={f(0)\cdot S \over f(0)+(S-f(0))\cdot e^{-S\cdot k\cdot 2}}$

$\Leftrightarrow 126.079={122.034\cdot 3.104.160 \over 122.034+(3.104.160-122.034)\cdot e^{-3.104.160\cdot k\cdot 2}}$

$\Leftrightarrow 122.034+(3.104.160-122.034)\cdot e^{-3.104.160\cdot k\cdot 2}={122.034\cdot 3.104.160 \over 126.079}$

$\Leftrightarrow e^{-3.104.160\cdot k\cdot 2}={122.034\cdot 3.104.160 \over 126.079\cdot (3.104.160-122.034)}-{122.034 \over 3.104.160-122.034}$

$\Leftrightarrow e^{-3.104.160\cdot k\cdot 2}={122.034\cdot 3.104.160 \over 126.079\cdot 2.982.126}-{122.034 \over 2.982.126}$

$\Leftrightarrow -3.104.160\cdot k\cdot 2=ln({122.034\cdot 3.104.160 \over 126.079\cdot 2.982.126}-{122.034 \over 2.982.126})$

$\Leftrightarrow k={ln({122.034\cdot 3.104.160 \over 126.079\cdot 2.982.126}-{122.034 \over 2.982.126}) \over -6.208.320}$

$\Leftrightarrow k\approx 5,4711\cdot 10^{-9}$

Allgemein ergibt sich nun folgende Gleichung:

$f(t)={\frac {122.034\cdot 3.104.160}{122.034+(3.104.160-122.034)\cdot e^{-3.104.160\cdot 5,4711\cdot 10^{-9}\cdot t}}}$

Zur Bestimmung der Zahl der Migranten, die sich 2026 in Rheinland-Pfalz befinden, wird nun $t=8$ in $f$ eingesetzt.

$f(8)={\frac {122.034\cdot 3.104.160}{122.034+(3.104.160-122.034)\cdot e^{-3.104.160\cdot 5,4711\cdot 10^{-9}\cdot 8}}}=138.998,0903$

Somit leben im Jahr 2026 138.998 Migranten in Rheinland-Pfalz. Nun ist von Interesse, wie viele Menschen zwischen 2020 und 2026 hinzu gekommen sind. Dafür wird die folgende Differenz gebildet:

$138.998-126.079=12.919$

Folglich sind 12.919 Menschen von 2020-2026 nach Rheinland-Pfalz gewandert.

Um nun die Zahl der Kinder zwischen 10 und 15 Jahren unter den Migranten zu ermitteln, werden die Altersstrukturen der Länder (von 2020) betrachtet. Die Bevölkerungspyramiden liefen jedoch nur den Prozentanteil der Kinder zwischen 10 und 14 Jahren und zwischen 15 und 19 Jahren. Somit muss der Anteil der 15-Jährigen zu dem Anteil der 10- bis 14-Jährigen addiert werden. Zur Bestimmung des Anteils der 15-Jährigen wird eine Gleichverteilung in der Altersklasse der 15- bis 19-Jährigen angenommen. Daraus folgt, dass der Anteil der 15-Jährigen ein Fünftel des Anteils der 15- bis 19-Jährigen entspricht. Nun wird von den prozentualen Anteilen der migrierten Kinder zwischen 10 und 15 Jahren das arithmetische Mittel gebildet. Dies ist notwendig, da nicht jedes Land einzeln betrachtet werden kann.

Implementation Anteile der Migranten in Excel

Unter den 12.919 Menschen, die zwischen 2020 und 2026 nach Rheinland-Pfalz gewandert sind, sind 1.323 Kinder zwischen 10 und 15 Jahren, denn es gilt folgende Rechnung:

$12.919\cdot 0,1024=1.322,9056$

Migration bis 2020

Nun müssen noch die Kinder betrachtet werden, die nicht in Deutschland geboren sind und bis 2020 nach Rheinland-Pfalz gewandert sind. Hierbei müssen die 4- bis 9-Jährigen betrachtet werden, da sich diese Kinder im Jahr 2026 in der Sekundarstufe 1 befinden. Die Argumentation und Rechnung verläuft analog zu der Bestimmung der 10- bis 15-Jährigen im vorherigen Punkt.

Implementation der Migrantenanteile bis 2020 in Excel

Aus der Tabelle lässt sich somit ablesen, dass im Jahr 2020 13.427 Kinder im Alter von 4 bis 9 Jahren in Rheinland-Pfalz leben.

Nun werden alle Werte addiert und es ergibt sich die Schülerzahl für das Jahr 2026: $199.329+1.323+13.427=214.079$

Vergleich 2022

Um eine konkrete Aussage über den Lehrerbedarf zu treffen, müssen zum Vergleich die Schülerzahlen in der Sekundarstufe 1 in Rheinland-Pfalz für das Jahr 2022 bestimmt werden. Dies verläuft analog zu der Bestimmung der Schülerzahlen für das Jahr 2026 und wird daher im folgenden abgekürzt.

Die Geburtenzahlen von 2007 bis 2012 geben unter Berücksichtigung der Kindersterblichkeit eine Aussage über die Anzahl der Einschulungen in die 5.Klasse.

Bundesland Rheinland-Pfalz

Jahr	Anzahl Geburten	Jahr	Anzahl Einschulungen 5.Klasse
2007	32.536	2017	32.406
2008	32.223	2018	32.094
2009	30.881	2019	30.757
2010	31.574	2020	31.448
2011	31.081	2021	30.957
2012	31.169	2022	31.044
$\sum$	189.464	$\sum$	188.706

Zur Bestimmung der Migranten, die sich 2022 in Rheinland-Pfalz befinden, wird $t=4$ in $f$ eingesetzt.

Es gilt: $f(4)=130.252,2223$

Danach wird die Differenz zwischen den Jahren 2022 und 2020 gebildet: $130.252-126.079=4.173$

Somit sind 4.173 Menschen in den zwei Jahren nach Rheinland-Pfalz gewandert. Darunter sind 427 Kinder zwischen 10 und 15 Jahren, da $4173\cdot 0,1024=427,3152$.

Da die Kinder 2022 zwischen 10 und 15 Jahren alt sein sollen, betrachtet man nun die 8- bis 13-Jährigen, die bereits vor 2020 nach Rheinland-Pfalz gewandert sind.

Implementierung der Migrantenanteile 2020 in Excel

Nun werden alle Werte addiert und die Schülerzahl für das Jahr 2022 steht fest: $188.706+427+13.228=202.361$

Software

Tabellenkalkulation

Zur Implementation der Daten wurde das Tabellenkalkulationsprogramm Excel verwendet. Neben Excel kann auch das Open Source Programm LibreOffice Calc benutzt werden.

Implementation der Migranten 2018 & 2020 in Excel

• Einwohnerzahl der Herkunftsländer und Migrantenzahl in Deutschland bekannt
• Migrantenzahl in Rheinland-Pfalz soll bestimmt werden
• (D2) Befehl für die Migranten aus Ägypten in RLP (2018): =RUNDEN(0,05*C2;0)
• (F2) Befehl für die Migranten aus Ägypten in RLP (2020): =RUNDEN(0,05*E2;0)
• alle weiteren Länder analog
• (D11), (F11) Summe der in Rheinland-Pfalz lebenden Migranten über den Befehl: =SUMME(D2:D9) bzw. =SUMME(F2:F9)

Implementation Anteile der Migranten in Excel

• Anteil der 10- bis 14-Jährigen und 15- bis 19-Jährigen aus den Bevölkerungsdiagrammen der Länder entnommen
• Anteil der 15-Jährigen aus dem Anteil der 15- bis 19-Jährigen bestimmt
• (D2) 15-Jährige in Ägypten über den Befehl: =C2*0,2
• (E2) Damit 10- bis 15-Jährige in Ägypten über den Befehl: =B2+D2
• alle weiteren Länder analog
• (E12) Arithmetischer Mittelwert über den Befehl: =MITTELWERT(E2:E9)

Implementation der Migrantenanteile bis 2020 in Excel

• Anteil der 0- bis 4-Jährigen und 5- bis 9-Jährigen aus den Bevölkerungsdiagrammen der Länder entnommen
• Anteil der 4-Jährigen aus dem Anteil der 0- bis 4-Jährigen bestimmt
• (C2) 4-Jährige in Ägypten über den Befehl: =B2*0,2
• (E2) Damit 4- bis 9-Jährige in Ägypten über den Befehl: =C2+D2
• Migrantenzahl in Rheinland-Pfalz (2020) aus vorherigen Berechnungen bekannt
• (G2) Ägyptische Kinder zwischen 4 und 9 Jahren in Rheinlandpfalz über den Befehl: =RUNDEN(E2*F2;0)
• alle weiteren Länder analog
• (G12) Summe aller migrierten Kinder zwischen 4 und 9 Jahren in Rheinland-Pfalz (2020) über den Befehl: =SUMME(G2:G9)

wxMaxima

Zur Bestimmung der Funktionswerte für $t\in \{0,2,4,8\}$ wird wxMaxima verwendet.

Maxima 3.Zyklus Funktionswerte

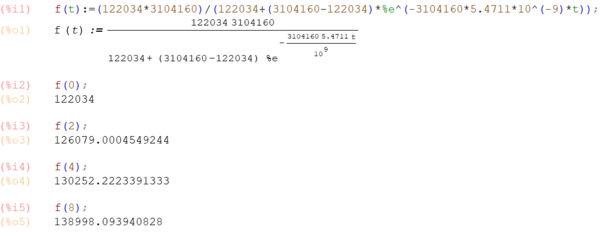
Resultate der Modellierung

Im Jahr 2026 sind 214.079 Schüler in der Sekundarstufe 1.

Lehrerbedarf?

Die folgende Tabelle zeigt die Anzahl der Schüler und Mathematiklehrkräfte in den Jahren 2022 und 2026. Im direkten Vergleich dieser Zahlen lässt sich bereits sagen, dass die Zahl der Schüler bis 2026 zunehmen wird, während die Zahl der Mathematiklehrkräfte abnimmt.

Zur Beurteilung, ob im Jahr 2026 Lehrerbedarf bzw. Lehrermangel vorliegt, wird das Verhältnis Schüler pro Mathematiklehrer gebildet. Im Jahr 2022 betreut ein Mathematiklehrer circa 25 Schüler, im Jahr 2026 sind es circa 27 Schüler. Somit muss eine Lehrperson im Jahr 2026 mehr Schüler betreuen als im Jahr 2022.

Dies kann zu einem Qualitätsverlust im Mathematikunterricht führen. Bildungspolitiker sollten daher handeln [1].

Bundesland Rheinland-Pfalz

Jahr	Anzahl Schüler	Anzahl Mathematiklehrkräfte	Schüler pro Mathematiklehrer*
2022	202.361	8.038	25,1755
2026	214.079	7.857	27,2469

(*Die Schülerzahl pro Mathematiklehrkraft darf nicht als Schülerzahl in einer Klasse interpretiert werden. Hier geht es um das direkte Betreuungsverhältnis eines Lehrers. Im Vergleich dazu lag das Verhältnis Schüler pro Lehrer allgemein in der Sekundarstufe an einem Gymnasium im Jahr 2019 bei 14,8 . Dieser Wert resultiert aus einer komplexeren Berechnung der Schüler-Lehrer-Relation und ist nicht mit dem Wert in diesem Modell gleichzusetzen. Dennoch ist dieser Wert deutlich geringer, weshalb somit auch auf einen Mathematiklehrermangel geschlossen werden kann.)

Bewertung und Optimierung

• Kritik: Sättigungsgrenze $S$ als geschätzter Wert ungenau

→ Optimierung: Die Konstante $S$ wird durch $S_{t}$ ersetzt

$f(t)={\frac {f(0)\cdot S}{f(0)+(S-f(0))\cdot e^{-S\cdot k\cdot t}}}$ ⇒ $f(t)={\frac {f(0)\cdot S_{t}}{f(0)+(S_{t}-f(0))\cdot e^{-S_{t}\cdot k\cdot t}}}$

Dabei ist $S_{t}=EW_{t}\cdot MD_{t}\cdot MRP_{t}$

$EW_{t}$ beschreibt die Zahl der Einwohner in den Herkunftsländern zum Zeitpunkt $t$ (in diesem Zyklus: 310.416.000)

$MD_{t}$ beschreibt den Anteil der Migranten, die zum Zeitpunkt $t$ nach Deutschland wandern (in diesem Zyklus: 20%)

$MRP_{t}$ beschreibt den Anteil der Migranten, die zum Zeitpunkt $t$ nach Rheinland-Pfalz wandern (in diesem Zyklus: 5%)

Einwohnerzahlen sind keine statischen Größen und können daher Schwankungen unterliegen. Die Anteile der Migranten, die nach Deutschland $MD_{t}$ oder Rheinland-Pfalz $MRP_{t}$ wandern, sind ebenfalls nicht konstant. Schwankungen lassen sich durch Faktoren wie Klimawandel, Naturkatastrophen, politischer Lage oder Krieg erklären.

Es wurden folgende Aspekte nicht berücksichtigt:

• Kinder, die in Rheinland-Pfalz geboren sind und vor Eintritt in die Sekundarstufe abwandern (z.B. in andere Bundesländer)
• Kinder und ältere Menschen migrieren deutlich weniger

→ repräsentativ werden die Zahlen der Bevölkerungspyramide für die Altersstruktur genommen, obwohl das nicht der Altersstruktur der Migranten entspricht

• Gewichtung des Mittelwertes (arithmetisches Mittel verwendet)
• Migranten aus verschiedenen Herkunftsländern können sich unterschiedlich auf die Bundesländer verteilen

• (Altersverteilung verschiebt sich bis zum Schuleintritt)

Mathematische Theorie für die Modellierungszyklen

Zyklus 1: Sekundarstufe I

Prozentrechnung

Prozentangaben dienen dazu, auszudrücken, wie groß der Anteil eines Teils des Ganzen am gesamten Ganzen ist. Der Grundgedanke ist dabei, dass man sich das Ganze in Hundertstel aufgeteilt denkt.

Ein Prozent ist dann ein Hundertstel des Ganzen. $100\%$ entspricht dem Ganzen, das ist dann der Grundwert. $1\%$ entspricht also ${\frac {1}{100}}$ des Grundwertes.

• Der Grundwert $G$ steht für das Ganze, von dem im Zusammenhang der Aufgabenstellung ausgegangen werden soll. $G={\frac {W}{p}}\cdot 100$

"Von $24$ Schülern einer Klasse..."

• Der Prozentwert $W$ ist der Teil des Ganzen, um den es im betreffenden Sachzusammenhang geht. $W={\frac {p\cdot G}{100}}$

"... mögen $6$ Schüler keine Prozentrechnung."

• Der Prozentsatz $p$ ist der in $\%$ ausgedrückte Anteil, den der Prozentwert am Grundwert hat. $p={\frac {W\cdot 100}{G}}$

"Das sind $25\%$ der Klasse."

Parameterfunktion

Unter Parameterfunktionen versteht man in der Analysis Funktionen, in deren Funktionsterm außer der unabhängigen Variablen noch ein oder mehrere konstante Parameter auftreten. Variiert man solch einen Parameter, erhält man eine Menge von miteinander verwandten Funktionen.

Die Auswirkungen von Parametern auf Funktionsgraphen allgemein:

$g(x)=a\cdot f(b\cdot (x+c))+d$

Dabei:

• Streckung in $y$-Richtung $|a|>1$
• Stauchung in $y$-Richtung $0<|a|<1$
• Streckung in $x$-Richtung $0<|b|<1$
• Stauchung in $x$-Richtung $|b|>1$

• Verschiebung in $x$-Richtung nach links $c>0$
• Verschiebung in $x$-Richtung nach rechts $c<0$
• Verschiebung in $y$-Richtung nach oben $d>0$
• Verschiebung in $y$-Richtung nach unten $d<0$

Trigonometrische Regression

Gegeben:

• Menge von Wertepaaren $(x_{i},y_{i})$
• Trigonometrische Funktion $f(x)=a\cdot sin\cdot (bx+c)+d$

Ziel der trigonometrischen Regression ist es, die Parameter a,b und c so zu wählen, dass die Menge der Wertepaare möglichst gut approximiert wird. Das bedeutet, dass die minimale Fehlerquadratsumme

$\Sigma (f(x_{i})-y_{i})^{2}$ so klein wie möglich sein soll.

Zyklus 2: Sekundarstufe II

Matrizen

• Matrix allgemein

Ein Zahlenschema mit $m$ Zeilen und $n$ Spalten wird als $m\times n-Matrix$ bezeichnet $(m,n\in \mathbb {N} )$. Ist $m=n$, dann ist die Matrix quadratisch. Die Einträge in der Matrix heißen Elemente $a_{ij}$ $(a\in \mathbb {R} )$, dabei ist $i$ die Zeilennummer und $j$ die entsprechende Spaltennummer. ${\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &a_{nn}\end{pmatrix}}$

• Matrizenmultiplikation

Eine Multiplikation $C=A\cdot B$ für Matrizen ist nur dann definiert, wenn die Matrix $A$ genau so viele Spalten hat, wie die Matrix $B$ Zeilen besitzt. Damit ist sie im Allgemeinen nicht kommutativ.

$A={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\\end{pmatrix}},$ $B={\begin{pmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\\b_{31}&b_{32}\\\end{pmatrix}},$

$C=A\cdot B={\begin{pmatrix}a_{11}\cdot b_{11}+a_{12}\cdot b_{21}+a_{13}\cdot b_{31}&a_{11}\cdot b_{12}+a_{12}\cdot b_{22}+a_{13}+b_{32}\\a_{21}\cdot b_{11}+a_{22}\cdot b_{21}+a_{23}\cdot b_{31}&a_{21}\cdot b_{12}+a_{22}\cdot b_{22}+a_{23}+b_{32}\\\end{pmatrix}}$

• Stochastische Matrizen

Eine Matrix $P$ heißt stochastische Matrix, wenn sie quadratisch ist und für jedes ihrer Elemente $a_{ij}$ gilt $0\leq a_{ij}\leq 1$. Zudem muss die Summe der Elemente in jeder Spalte 1 betragen. Der zu einer stochastischen Matrix gehörende Prozess heißt Austauschprozess. Bei einem Austauschprozess gibt das Element $a_{ij}$ der zugehörigen stochastischen Matrix an, welcher Anteil der Objekte im Zustand $j$ sich bei der nächsten Beobachtung im Zustand $i$ befindet. $P={\begin{pmatrix}0,7&0,3&0,2\\0,1&0,6&0,4\\0,2&0,1&0,4\end{pmatrix}}$

Im Fall von $P$ gibt die stochastische Matrix das Wechselverhalten an, beispielsweise bei den Kunden eines Cafés. Die Matrix wird so gelesen, dass in den Spalten die Cafés stehen, von denen die Kunden weggehen und in den Zeilen die Cafés stehen, in die die Kunden wechseln. Also von wo nach wo die Kunden wechseln. Konkret bleiben in diesem Beispiel also $70\%$ der Kunden dem Café A treu, während $20\%$ der Kunden von Café A zum Café C wechseln. Von Café B nach Café A wechseln beim nächsten Besuch $30\%$ der Kunden usw.

Zyklus 3: Uni-Niveau

Logistisches Wachstum

Logistisches Wachstum ist ein Modell, welches oft für Wachstumsprozesse verwendet wird. Dabei wird das Modell des exponentiellen Wachstums durch eine bestimmte Schranke angepasst, um eine gewisse Sättigung mit einzubeziehen. Zu Beginn verläuft der Wachstumsprozess somit exponentiell und bei Annäherung an eine Grenze wird der Prozess durch ein beschränktes Wachstumsmodell beschrieben.

$f(t)={\frac {a\cdot S}{a+(S-a)\cdot e^{-S\cdot k\cdot t}}}$

• $a$: Anfangswert zum Zeitpunkt $t=0$ mit $0<a<S$
• $S$: Sättigungsgrenze (Wert, der maximal möglich ist) mit $S=\lim _{t\to \infty }f(t)$
• $k$: Wachstumskonstante

Um eine geeignete Funktion zu erhalten, für die die Parameter der jeweiligen Situation entsprechen, muss zunächst eine Sättigungsgrenze $S$ geschätzt werden. Außerdem benötigt man den zum Zeitpunkt $t=0$ entsprechenden Wert $a$. Um die Wachstumskonstante $k$ zu bestimmen, wird ein weiteres Wertepaar (z.B. $(u|v),t=u$ und $f(u)=v$) benötigt. Sind alle Werte vorhanden, können diese in die Formel für das logistsiche Wachstum eingesetzt werden.

Es ergibt sich $v={\frac {a\cdot S}{a+(S-a)\cdot e^{-S\cdot k\cdot u}}}$ ${\overset {(*)}{\Leftrightarrow }}$ $k={\frac {ln({\frac {a\cdot S-v\cdot a}{v\cdot (S-a)}})}{(-S)\cdot u}}$

[(*) nach k auflösen]

Bezüge zu anderen Modellierungsprojekten

[2]:Lehrerbedarf in Deutschland

Gruppenmitglieder

• Lara Marie Drexler
• Emily Reiser
• Anna Schieler
• Helena Vogel