Kurs:Algorithmen und Datenstrukturen/Vorlesung/Graphen Typen
Typen von Graphen und Anwendungen
[Bearbeiten]In diesem Kapitel werden Graphen behandelt. Ein Graph ist das mathematische Modell eines Netzwerks bestehend aus Knoten und Kanten. Graphen haben einen vielfältigen Einsatz. So kommen sie bei Verbindungsnetzwerken (Bahnnetz, Flugververbindungen, Straßenkarten, ...), Verweisen (WWW, Literaturverweise, Wikipedia, symbolische Links, ...), Technischen Modellen (Platinen-layout, finite Elemente, Computergrafik) und Software Reengineering und - dokumentation zum Einsatz. Bäume und Listen sind spezielle Graphen.
Ungerichteter Graph
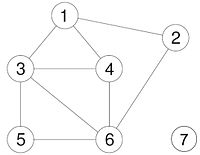
[Bearbeiten]Es gibt verschiedene Typen von Graphen. Der ungerichtete Graph ist beispielsweise eine Straßenverbindung, eine Telefonnetz oder ein soziales Netzwerk. Ein ungerichteter Graph ist ein Tupel G=(V,E). Wir haben eine endliche Menge V von Knoten (Vertices) und eine Menge E von Kanten (Edges), die aus ungeordneten Paaren aus V besteht. Es gilt, dass und jedes ist eine zweielementige Teilmenge der Knotenmenge . Im ungerichteten Graphen gibt es keine Schleifen, das heißt es gibt keine Kanten die von einem Knoten zu sich selbst laufen. Außerdem gibt es keine mehrfachen Kanten zwischen zwei Knoten, Parallelkanten genannt.
Hier können zum Beispiel die kürzesten Wege bei sozialen Netzwerken wie Facebook berechnet werden.
Spezielle Graphen
[Bearbeiten]Sei ein Graph.
G heißt planar, falls er ohne Überschneidungen der Kanten in der Ebene gezeichnet werden kann.
G heißt vollständig, falls
G heißt regulär, falls alle Knoten denselben Grad haben
G heißt bipartit, falls und
- keine zwei Knoten in sind adjazent
- keine zwei Knoten in sind adjazent
Beispiele
[Bearbeiten]Dieser Graph ist sowohl planar, regulär als auch vollständig.

Dieser Graph ist jedoch nur regulär und vollständig.

Hier handelt es sich nur um einen regulären Graphen.

Dies ist ein Beispiel für einen bipartiten Graph.

Gerichteter Graph
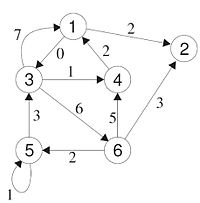
[Bearbeiten]Der gerichtete Graph ist beispielsweise eine Förderanlage oder ein Kontrollfluss in Programmen. Der gerichtete Graph (auch Digraph) ist ein Tupel G=(V,E) mit V als endliche Menge von Knoten und E einer Menge von Kanten, geordneten Paaren aus V. Jedes ist nun ein Tupel e=(a,b) mit . Schleifen der Form (a,a) sind nun erlaubt. Dazu ist (a,b) eine andere Kante als (b,a). Der Unterschied zwischen (a,b) und {a,b} besteht darin, dass das Tupel (a,b) geordnet ist. Die Reihenfolge kann nicht verändert werden. Hingegen ist {a,b} eine Menge, in der die Reihenfolge der Elemente keine Rolle spielt.
Gerichtete Graphen werden zum Beispiel als Web-Graph (Google`s PageRank) benutzt. Aber auch in der Scientometrie kommen sie zum Einsatz bei der Impact Faktoren Berechnung. Bei Datenstrukturen im Semantik Web werden gerichtete Graphen zum Speichern von Daten genutzt.
Gerichtete und ungerichtete Graphen
[Bearbeiten]Ein ungerichteter Graph kann in einen gerichteten Graphen transformiert werden, indem jede ungerichtete Kante {v,w} durch zwei gerichtete Kanten (v,w) und (w,v) ersetzt wird. Dann ist beispielsweise der Zusammenhang identisch mit dem starken Zusammenhang. Dazu haben gerichtete Graphen eine größere Ausdrucksstärke und daher wird "Graph" oft als Synonym für einen Digraph verwendet.
Gewichteter Graph
[Bearbeiten]Ein ungerichteter gewichteter Graph ist beispielsweise eine Flugverbindung mit Meilen oder Kosten, ein Straßennetz mit Kilometern oder ein Rohrsystem mit Durchfluss.
Ein gerichteter gewichteter Graph ist beispielsweise ein Straßennetz mit Einbahnstraßen, Rohre mit Ventilen oder ein Förderband.
Der Graph ist ein Paar G=(V,E) und wir haben eine Kantengewichtsfunktion g. Daraus erhalten wir G=(V,E,g) mit . Der Graph kann gerichtet oder ungerichtet sein und die Kantengewichte müssen nicht notwendigerweise natürliche Zahlen sein.
Ungerichtete gewichtete Graphen kommen zum Beispiel bei der Navigation beim Berechnen des kürzesten Weges zum Einsatz.
Gerichtete gewichtete Graphen kommen bei der Optimierung in der Telekommunikation zum Einsatz.
Hypergraph
[Bearbeiten]Es gibt aber noch viele weitere Varianten von Graphen wie Multigraphen oder Hypergraphen.
Ein Hypergraph ist ein Paar G=(V,E) mit einer Menge von Knoten V und einer Menge von Hyperkanten .