Kurs:Funktionalanalysis/Quotientenraum

Einleitung

Der Quotientenvektorraum, auch kurz Quotientenraum oder Faktorraum genannt, ist ein Begriff aus der linearen Algebra, einem Teilgebiet der Mathematik. Er ist derjenige Vektorraum, der als Bild einer Parallelprojektion entlang eines Untervektorraums entsteht. Die Elemente des Quotientenvektorraumes sind Äquivalenzklassen. In einem Quotientenvektorraum entspricht der Nullvektor dem Untervektorraum bzgl. dem der Quotientenraum gebildet wird. Alle anderen Elemente entstehen durch Verschiebung des Untervektorraumen mit einem Repräsentanten des Vektorraumes.

Definition: Aquivalenzrelation

Es sei $V$ ein Vektorraum über einem Körper $K$ und $U$ ein Untervektorraum von $V$ . Durch die Festsetzung

v_{1}\sim v_{2}\;:\!\iff v_{1}-v_{2}\in U

für

v_{1},v_{2}\in V

wird auf $V$ eine Äquivalenzrelation definiert.

Geometrische Interpretation

Die Vektoren $v_{1}$ und $v_{2}$ sind also äquivalent, wenn sie sich um einen Vektor aus $u\in U$ unterscheiden. Betrachtet man z.B. eine Gerade als eindimensionalen Untervektorraum $U$ durch den Ursprung, so kann man die Äquivalenz zweier Vektor $v_{1}$ und $v_{2}$ geometrisch wie folgt ausgedrücken:

Wenn die Gerade durch die Punkte

v_{1}

und

v_{2}

parallel zur durch

U

definierten Gerade ist, sind

v_{1}

und

v_{2}

äquivalent.

Äquivalenzklassen

Die Äquivalenzklasse eines Punktes $v$ ist

[v]:=v+U:=\{v+u\mid u\in U\}

,

anschaulich der zu $U$ „parallele“ affine Unterraum durch $v$ . Die Äquivalenzklassen werden auch als Nebenklassen bezeichnet (dieser Begriff stammt aus der Gruppentheorie).

Definition: Quotientenvektorraum

Der Quotientenvektorraum von $V$ nach $U$ ist die Menge aller Äquivalenzklassen und wird mit $V/U$ bezeichnet:

V/U:=\{[v]\mid v\in V\}

.

Er bildet einen Vektorraum, wenn die Vektorraumoperationen vertreterweise definiert werden:

$[v_{1}]+[v_{2}]=[v_{1}+v_{2}]$
$\lambda \cdot [v]=[\lambda v]$

für $v,v_{1},v_{2}\in V$ und $\lambda \in K$ .

Wohldefiniertheit der Operationen

Diese Operationen sind wohldefiniert, also von der Wahl der Vertreter unabhängig, d.h.

Für $v_{1},v_{2}\in [v]$ und $w_{1},w_{2}\in [w]$ gilt auch $[v_{1}+w_{1}]=[v_{2}+w_{2}]$
Für $v_{1},v_{2}\in [v]$ und $\lambda \in \mathbb {K}$ gilt auch $[\lambda \cdot v_{1}]=[\lambda \cdot v_{2}]$

bzw.

Für $v_{1}\in [v]$ und $w_{1}\in [w]$ gilt auch $[v_{1}+w_{1}]=[v+w]$
Für $v_{1}\in [v]$ und $\lambda \in \mathbb {K}$ gilt auch $[\lambda \cdot v_{1}]=[\lambda \cdot v]$

Beweisidee für den Nachweis der Wohldefiniertheit

Man zeigt jeweils zwei Mengeninklusionen für die Repräsentatenunabhängigkeit der definierten Operationen:

Seien $v_{1}\in [v]$ und $w_{1}\in [w]$ beliebig gewählt. Man zeigt $v_{1}+w_{1}\in [v+w]$ bzw. $[v]+[w]\subseteq [v+w]$
Für $v_{1}\in [v]$ und $\lambda \in \mathbb {K}$ zeigt man $\lambda \cdot v_{1}\in [\lambda \cdot v]$ bzw. $\lambda \cdot [v_{1}]\subseteq [\lambda \cdot v]$

Aufgabe für Studierende

Betrachten Sie die Inklusionen $[v]+[w]\subseteq [v+w]$ und $\lambda \cdot [v_{1}]\subseteq [\lambda \cdot v]$ . In meisten Fällen gilt sogar die Mengengleichheit $[v]+[w]=[v+w]$ und $\lambda \cdot [v_{1}]=[\lambda \cdot v]$ . Bestimmen Sie die Fälle, in denen eine echte Teilmengenbeziehung vorliegt!

Mengeninklusion für den Nachweis der Wohldefiniertheit

Exemplarisch wird für $v_{1}\in [v]$ der Nachweis Mengeninklusion $\lambda \cdot [v_{1}]\subseteq [\lambda \cdot v]$ geführt (Beweisen Sie die anderen 3 Mengeninklusionen analog als Übung):

Sei $x\in [\lambda \cdot v_{1}]$ , dann gilt es ein $u_{1}\in U$ mit $x=\lambda \cdot v_{1}+u_{1}\in [\lambda \cdot v_{1}]$ .
Ferner gibt es mit $v_{1}\in [v]$ ein $u_{2}\in U$ mit $v_{1}=v+u_{2}\in v+U=[v]$ .
Insgesamt erhält man: $x=\lambda \cdot v_{1}+u_{1}=\lambda \cdot (v+u_{2})+u_{1}=\lambda \cdot v+(\underbrace {\lambda \cdot u_{2}+u_{1}} _{\in U})\in [\lambda \cdot v]$ .

Ideal und Multiplikation

Ist $A$ eine Algebra und der Untervektorraum $U\subseteq A$ zugleich auch ein Ideal, dann kann man auch eine wohldefinierte Multiplkation auf dem Quotientenraum $A/U$ odefinieren. Für die Multiplikation im Quotientenraum $A/U$ muss man wieder die Repräsentantenunabhängigkeit nachweisen. Also mit $v_{1}\in [v]$ und $w_{1}\in [w]$ gilt auch:

v_{1}\cdot w_{1}\in [v\cdot w]

Zeigen Sie die Repräsentantenunabhängigkeit der Multiplikation im Quotientenraum!

Eigenschaften 1

Es gibt eine kanonische surjektive lineare Abbildung

\pi \colon \;V\to V/U,\;v\mapsto [v]

.

Ist $W$ ein Komplement von $U$ in $V$ , d. h. ist $V$ die direkte Summe von $U$ und $W$ , so ist die Einschränkung von $\pi$ auf $W$ ein Isomorphismus. Es gibt aber keine kanonische Möglichkeit, $V/U$ als Unterraum von $V$ aufzufassen.

Ist $V$ endlichdimensional, dann ergibt sich daraus die folgende Beziehung für die Dimensionen:

\dim U+\dim V/U=\dim V

Eigenschaften 2

Der Dualraum von $V/U$ kann mit denjenigen Linearformen auf $V$ identifiziert werden, die auf $U$ identisch $0$ sind.

Der Homomorphiesatz besagt, dass eine lineare Abbildung $f\colon \;V\to W$ einen Isomorphismus

V/(Kern(f))\to \mathrm {Im} (f)

zwischen dem Quotientenraum von

V

nach dem Kern von

f

und dem Bild von

f

induziert, d. h. die Verkettung

V\longrightarrow V/(Kern(f))\longrightarrow \mathrm {Im} (f)\longrightarrow W

ist gleich

f

.

Anwendung in der Funktionalanalysis

Viele normierte Räume entstehen auf die folgende Weise: Sei $V$ ein reeller oder komplexer Vektorraum und sei $p$ eine Halbnorm auf $V$ . Dann ist $U=\{v\in V\mid p(v)=0\}$ ein Untervektorraum von $V$ . Der Quotientenraum $V/U$ wird dann mit der Norm $[v]\mapsto p(v)$ ein normierter Vektorraum.

Allgemeiner: Sei $V$ ein topologischer Vektorraum, der nicht hausdorffsch ist. Dann lässt sich analog zu oben ein Unterraum definieren: $U=\{v\in V\mid {\text{Jede }}0{\text{-Umgebung enthält }}v\}={\overline {\{0\}}}$ . Der Quotientenraum $V/U$ wird mit der Quotiententopologie ein hausdorffscher topologischer Vektorraum.

Beispiele

Die folgenden Beispiele zeigen mathematische Anwendung für Quotientenräume:

$L^{p}$ -Räume
Unterräume, die durch Halbnormen definiert werden,
gemeometrische Interpretation

Abstrakt

Die $L^{p}$ -Räume sind Quotientenräume bei denen man Funktionen in einer Äquivalenzklasse zusammenfasst, die sich nur auf Nullmengen unterscheiden. Mit dieser Bemerkung für $L^{p}$ -Räume sind auch die Sobolew-Räume Quotientenvektorräume.

Konkret

Gegeben sei der Vektorraum $V=\mathbb {R} ^{2}$ und der eindimensionale Untervektorraum

U=\left\{\left.{\bigl (}{\begin{smallmatrix}x\\x\end{smallmatrix}}{\bigr )}\right|x\in \mathbb {R} \right\}

.

Dann ist zum Beispiel

{\bigl (}{\begin{smallmatrix}42\\12\end{smallmatrix}}{\bigr )}+U:=\left\{\left.{\bigl (}{\begin{smallmatrix}42\\12\end{smallmatrix}}{\bigr )}+u\,\right|u\in U\right\}

eine Äquivalenzklasse des Quotientenraumes $V/U$ .

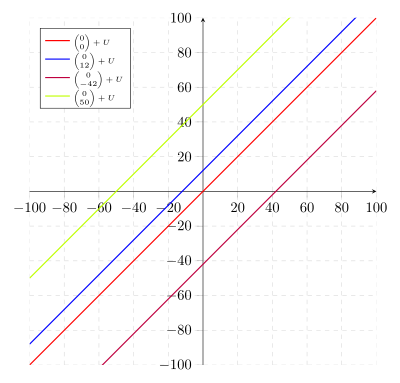
Geometrische Darstellung von Quotientenräumen

Anschaulich ist jede Gerade, die parallel zur winkelhalbierenden Gerade des 1. Quadranten ist, eine Äquivalenzklasse:

Siehe auch

Literatur

Gerd Fischer: Lineare Algebra. Vieweg-Verlag, lSBN 3-528-97217-3.
Klaus Jänich: Lineare Algebra. Springer-Lehrbuch, lSBN 3-540-66888-8.

Seiteninformation

Diese Lernresource wurde als Wiki2Reveal Foliensatz erstellt.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Funktionalanalysis' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Funktionalanalysis/Quotientenraum
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

Wikipedia2Wikiversitsy

Diese Seite basiert auf einer Wikipedia-Quelle, die dann als Wiki2Reveal-Präsentation in dieser Lernressource verwandelt wurde.