Kurs:Mathematische Modellbildung/Themen/Biodiversität
Gruppenthema 2: Modellierung von Biodiversitätshotspots zur Beurteilung des Managements von Flächen
1. Gruppenmitglieder
[Bearbeiten]- Clara Bröning
- Behcet Öztürk
- Guillaume Blin
- Janine Klotz
Folien
[Bearbeiten]2. Modellierungsproblem
[Bearbeiten]2.1 Einleitung
[Bearbeiten]Es leben etwa 60% weniger Wirbeltiere auf der Erde als 1970, typische Vogelarten sind zwischen 1998 und 2009 um mehr als 36% zurückgegangen und es droht weltweit weiterer Verlust von bis zu einer Millionen Arten. [1] Doch nicht nur die Zahl der Tiere nimmt drastisch ab, sondern auch die Vielfalt der Artgemeinschaften und das viel schneller als es normal wäre. Grund dafür ist der Mensch.
Etwa 75% der terrestrischen Ökosysteme und 66% der Meeresfläche wurden vom Menschen stark verändert. [2] Auch das Artensterben ist heute zwischen zehn- bis einhundertmal höher als im Durchschnitt der letzen zehn Millionen Jahre. [3] Und trotzdem bleibt die Frage bestehen, warum ist Biodiversität wichtig? Je weniger Arten, desto anfälliger sind Ökosysteme durch Stress, Störungen oder Veränderungen von außen. (Quelle) Ein geschwächtes Ökosystem ist instabil und kann nur noch eingeschränkt funktionieren. Für Menschen ist das vor allem wichtig, weil nur ein stabiles Ökosystem weiterhin wichtige Ökosystemdienstleistungen aufrecht erhalten kann.
2.2 Warum Biodiversität?
[Bearbeiten]Als Biodiversität bezeichnen die Vereinten Nationen die Vielfalt aller lebenden Organismen, Lebensräume und Ökosysteme auf dem Land, im Süßwasser, in den Ozeanen sowie in der Luft. Diese biologische Vielfalt ist jedoch bedroht und in Deutschland gelten knapp ein Drittel aller Tier- und Pflanzenarten als gefährdet. Die Menge an Fluginsekten ist in den letzten dreißig Jahren um mindestens 75 % zurückgegangen und gut zweihundert Blütenpflanzenarten stehen in Deutschland auf der „Roten Liste“ für gefährdete Pflanzen.[4]
Je höher die Biodiversität, desto besser ist die Anpassungsfähigkeit der Ökosysteme bei Veränderungen der Umweltbedingungen und desto stabiler sind die erbrachten Ökosystemleistungen.[5]
Artenvielfalt dient der Stabilität der Ökosysteme und spielt eine wichtige Rolle in der Klimaregulation. Unterschiedliche Arten besetzen unterschiedliche Nischen im Ökosystem. Durch fehlen Arten werden Ökokreisläufe gestört und aus dem Gleichgewicht gebracht.
Gemäss Millennium Ecosystem Assessment [6] lassen sich die Leistungen der Ökosysteme unterteilen in Versorgungsleistungen, regulierende Leistungen, kulturelle Leistungen und unterstützende Leistungen.
- Versorgungsleistungen: Zahlreiche Güter wie Nahrungsmittel, Trinkwasser, Energieträger, Kleidungsfasern, Baumaterialien oder medizinische Wirkstoffe existieren nur dank der Vielfalt der Organismen. Die genetischen Ressourcen sind die Grundlage für die Entwicklung neuer Nutzpflanzen, Medikamente und industrieller Rohstoffe.
- Regulierende Leistungen: Natürliche Lebensgemeinschaften in Ökosystemen speichern CO2, schützen vor Lawinen und Hochwasser, verhindern Erosion, regulieren das Klima und sichern die Bestäubung von Wild- und Kulturpflanzen.
- Kulturelle Leistungen: Lebensräume mit all ihren Arten tragen zu vielfältigen Landschaften bei, mit denen sich die Menschen identifizieren. Die Erholungsleistung und die Ästhetik der Biodiversität sind beachtlich.
- Unterstützende Leistungen: Grundlegende Leistungen der Ökosysteme: Sauerstoffproduktion, die Bodenbildung und -fruchtbarkeit, die Aufrechterhaltung der Nährstoffkreisläufe und des Wasserkreislaufs.
2.3 Einordnung SDGs(Sustainable Development Goals)
[Bearbeiten]Die Sustainable Development Goals (die globalen Nachhaltigkeitziele) sind als Richtlinien zu verstehen, nach denen sich Regierungen weltweit, die Bevölkerung, die Wirtschaft und Wissenschaft richten sollen, um eine nachhaltige Entwicklung in ökonomischen, ökologischen und sozialen Aspekten zu erreichen. Die 17 Ziele decken viele Themen ab, wie soziale Gleichberechtigung, Stärkung nachhaltiger Wirtschaft und auch Themen zum Umwelt- und Klimaschutz.[7]

Unser Modellierungsthema kann einigen der Suststainable Development Goals direkt und indirekt zugeordnet werden. Eine direkte Verbindung besteht mit den Zielen 13, 14 und 15, welche „Maßnahmen zum Klimaschutz“, „Leben unter Wasser“ und „Leben an Land“ sind. [8] Diese Ziele sollen durch unsere Modellbildung unterstützt werden, da wir mithilfe unseres Modells eine Grundlage für monetäre Entscheidungen im Naturschutz und Flächenmanagement erstellen wollen. In den Zielen 13-15 geht es vor allem darum Ökosysteme zu schützen und unsere Bewirtschaftungs- und Nutzungsansprüche zu ändern.[9] Einige weitere SDGs sind indirekt mit unserem Modellierungsansatz verknüpft, so sind die Ziele 3, 6 und 12 ebenso wichtig und Teil unseres Themas. Die Ziele umfassen „Gesundheit und Wohlergehen“, „Sauberes Wasser und Sanitäreinrichtungen“ und „Nachhaltige/r Konsum und Produktion“.[10] An diesen Zielen sieht man die Relevanz von Biodiversität und funktionierenden Ökosystemen. Denn nur funktionierende Ökosysteme können relevante Ökosystemdienstleistungen aufrecht erhalten, wie zum Beispiel sauberes Wasser oder fruchtbaren Boden für die Landwirtschaft.
2.4. Ziel der Modellbildung
[Bearbeiten]Das Ziel unseres Modellierungsprozesses ist es Entscheidungsvorgänge bezüglich von Flächenmanagement einfacher zu gestalten durch die Betrachtung und Visualisierung von Biodiversitätshotspots. Durch diese von uns angestrebte visuelle Aufarbeitung soll schneller ersichtlich werden welche benachbarten Flächen unterschiedlich hohe Biodiversitäten aufweisen und wo es am sinnvollsten ist Gelder in Naturschutz und Management, mit dem Ziel höherer Biodiversität, zu stecken. Unser Modellierungszyklus wird beispielhaft an beispielhaften imaginären Habitaten und an Flächen in der Umgebung von Landau durchgeführt, soll aber als Modell auch mit den Daten der verschiedenen Nutzergruppen durchgeführt werden können.
2.5 Zielgruppe der Modellbildung
[Bearbeiten]- NGOs
- Naturschutzorganisationen & -behörden
- Ökologisch orientierte Unternehmen
All diese Nutzergruppen sollen durch unsere Modellierungsergebnisse besser basierte Entscheidungen für die Finanzierung von Naturschutz treffen können.
3. Modellierungszyklen
[Bearbeiten]3.1. Modellierungszyklus 1 – Niveau Sekundarstufe 1
[Bearbeiten]Diversität bedeutet laut Duden "Vielfalt", "Vielfältigkeit" [11] und auch im Kontext der Biodiversität geht es genau darum. Um Vielfalt der Ökosysteme, der genetischen Vielfalt und dem Reichtum an Arten [12].
Im weitesten Sinn ist Artenvielfalt die Anzahl von verschiedenen Arten an einem Ort, das wird auch Artenreichtum genannt. Diese reine Summe der Arten hat aber Limitationen in dem Vergleich von der Diversitäten verschiedener Artgemeinschaften, deshalb gibt es weitere Maße die zur Beschreibung entwickelt wurden. So wird in verschiedene Arten von Diversitäten unterteilt, es gibt die Alpha-, Beta- und Gamma-Diversität. Die Alpha-Diversität liegt sehr nah an dem Maß des Artenreichtums, sie beschreibt die Anzahl der Arten in einem bestimmten Habitat oder einer Gemeinschaft. Sie wird genutzt um die Artzahl in einem bestimmten Ökosystemen zu vergleichen, beispielsweise in Seen oder Wäldern. (Beispiel: 100 ha Wald in Deutschland sind artenärmer z.B. weniger Baumarten als 100 ha Wald im Amazonas Regenwald). Man kann Alpha-Diversität auch zwischen zwei oder mehr Habitaten vergleichen, man betrachtet dann den Mittelwert der Artenzahl der Regionen. Gamma-Diversität betrachtet sehr diverse Landschaften oder größere geographische Skalen, es geht um die Artzahl in eine großen Region (z.B. große Steppe/Prärie USA) oder einem Kontinent. Der Unterschied zwischen der Alpha-Diversität und der Gamma-Diversität besteht darin, dass Gamma-Diversität nur auf größeren Skalen betrachtet wird die Gemeinsamkeit der zwei Diversitäten besteht darin, dass beide den Zweck einer inventareschen Diversität besitzen. Beta-Diversität hängt mit den anderen zwei Diversitäten zusammen, sie gibt die Änderung der Artzusammensetzung entlang ökologischen oder geographischen Gradienten an. Die Beta-Diversität ist hoch, wenn in jedem Seen einer Region andere Arten vorkommen und die Artzusammensetzung so sehr verschieden ausfällt.
Die unterschiedlichen Diversitäten haben unterschiedliche Aussagekraft über die tatsächliche Biodiversität einer Raumordnung. Man betrachtet einen regionalen Zuwachs an Alpha-Diversität, aber eine globale Abnahme an Beta-Diversität. Die Problematik dahinter ergibt sich daraus, dass die Beta-Diversität die Differenzierung von Lebensräumen angibt und die gilt es zu schützen, da unsere Ökosysteme durch eine hohe Vielfalt und "Arbeitsteilung" gut schädliche Umwelteinflüssen abfangen können und somit resilienter und resistenter sind.
3.1.1 Datenerstellung
[Bearbeiten]
Die Daten wurden mithilfe von Tabellenkalkulation erstellt und es wurden kleinere Berechnungen mit dieser durchgeführt. Unser Beispiel, bestehen aus drei Regionen und soll beispielhaft zeigen, wie sich die verschiedenen Diversitäten errechnen lassen. Hierfür beinhaltet unser Beispiel drei Regionen, die aus jeweils drei Bergen bestehen. Die Artzusammensetzung, die unserem Schaubild zu entnehmen ist, variiert von Berg zu Berg. Vor allem in Regionen 1 überschneiden sich die Zusammensetzungen sehr und in Regionen 3 ist fast keine Überschneidung vorzufinden. Um die Diversitäten zu errechnen muss man nun verschieden vorgehen.
3.1.2. Erste Berechnung
[Bearbeiten]Wir haben uns in unserer Modellierung für diese Berechnung der Diversitäten entschieden und erheben keinen Anspruch auf Vollständigkeit, da es auch noch andere Ansätze zur Berechnung gibt und es auch weiterhin ein offenes Feld für Forschung innerhalb der Ökologie ist.
Alpha-Diversität, kann man bezogen auf ein Habitat berechnen oder vergleichend zwischen zwei bis mehreren Habitaten. Betrachtet man die Alpha-Diversität für nur eine Fläche so genüg zu zählen, wie viele Arten in der Gemeinschaft vorkommen, sie gilt deshalb auch als „inventarische Diversität“. Die Frage ist nach der Summe der vorkommenden Arten. Wenn man Alpha-Diversität vergleichend zwischen zwei oder mehr Habitaten betrachtet nimmt man den Mittelwert der Artenzahl aus der Anzahl der Regionen. In unserem Beispiel hat Region 1 drei Berge mit Berg 1 6 Arten, Berg 2 5 Arten und Berg 3 7 Arten. Wir errechnen den Mittelwert mit der Formel

a=Anzahl der Arten pro Berg
n=Anzahl der Berge
der errechnete Mittelwert liegt bei 6, das ist die Alpha-Diversität der drei Berge zusammengefasst.
Die Gamma-Diversität ergibt sich aus der Summe der Arten einer Region. In dem Beispiel ist die Gamma-Diversität in Region 1 sieben, da sieben verschiedene, sich nicht überschneidende Arten über die drei Berge verteilt vorkommen.
Die Beta-Diversität kann man aus den anderen zwei Diversitäten errechnen. Hierfür wird die Gamma-Diversität durch die mittlere Alpha-Diversität geteilt. In dem Beispiel liegt die Beta-Diversität bei 1,17, da 7/6=1,17. Die Beta-Diversität ist dann sehr hoch, wenn sehr unterschiedliche Artzusammensetzungen von Habitat zu Habitat in der Region vorkommen.
3.1.3. Berechnung mit Tabellenkalkulation
[Bearbeiten]
Die genutzten Befehle beliefen sich auf relativ einfache Funktionen der Tabellenkalkulation, was gut zur Veranschaulichung in der Sek. 1 hilft. Genutzt Befehle und unsere Vorgehensweise:
* die Artzahlen und - Zusammensetzungen wurden von uns frei gewählt und absichtlich in einem kleinen Zahlenraum belassen * zur Berechnung der Alpha-Diversität wurde =MITTELWERT() genutzt * die Gamma-D kann anhand unseres Schaubilds abgelesen werden, hierfür wird die Summe der sich nicht überschneidenden Arten genommen * die Beta-Diversität wurde mit =γ/α berechnet * die Zellen wurden für die Übersichtlichkeit mit zwei Nachkommastellen formatiert
So kann man mit den Schüler*innen den Mittelwert erst per Hand ausrechnen und dann in der Tabellenkalkulation prüfen, ob richtig gerechnet wurde.
Die Daten und das von uns genutzte Fallbeispiel wurden relativ simpel und vom Umfang gering gehalten um das Prinzip der drei verschiedenen Diversitäten einfach und verständlich zu erklären.
Ergebnisinterpretation
Betrachtet man nun die Ergebnisse entstehen sehr unterschiedliche Eindrücke. So hat die Region 1 laut der Alpha-Diversität die höchste Biodiversität, aber laut Beta-Diversität den geringsten Wert. Umgekehrt gilt das für Region 3, die die höchste Beta-Diversität aufweist, aber die niedrigste Alpha-Diversität. Und betrachtet man die Gamma-Diversität hat die Region 2 den höchsten Wert. Man muss differenzieren welche Diversität man betrachten will:
* Alpha-Diversität: Artenreichtum eines Habitats/einer Region * Beta-Diversität: Differenzierung der Artenzusammensetzung einer Region * Gamma-Diversität: Artenreichtum eines größeren Gebiets
3.1.4. Modellkritik
[Bearbeiten]Angefangen damit, dass das Feld der Berechnung der Biodiversität immer noch ein weites Feld in der Ökologie ist und es verschiedene Arten und Weisen gibt die Diversitäten zu berechnen, ist dieses Modell zur Berechnung der Alpha-, Beta- und Gamma-Diveristät ist nur begrenzt einsetztbar, da die Berechnung selbst an ihre Grenzen kommt, gerade der Punkt der Beta-Diversität muss anders betrachtet und berechnet werden (komplexer und differenzierter). Weiter ausführen!
Ein weiterer Kritikpunkt ist die starke Vereinfachung und Abstraktion eines so komplexen Systems, wie dem eines Ökosystems. Man braucht Modelle um eben diese komplexen Zusammenhänge erklären zu können und mit Ihnen rechnen zu können, dennoch ist die Vorgehensweise, die wir für den Modellierungszyklus 1 gewählt haben sehr stark vereinfacht und entspricht so weniger den realen Gegebenheiten.
Dennoch bietet dieser Einstieg ein gute Möglichkeit um den Begriff der Biodiversität zu verstehen.
3.2 Modellierungszyklus 2 – Niveau Sekundarstufe 2
[Bearbeiten]Wie hängen die Ressourcen und die Artenzahl miteinander zusammen? (z.B. Bienen und Blütenzahl)
3.2.1 Datenvorstellung Tabelle
[Bearbeiten]
Die Grunddaten für die Modellierung wurden im Sommersemester 2022 zwischen dem 01.-10. Juli an der Universität Landau im Seminar Organismen und ihre Umwelt erhoben. Es handelt sich dabei um von den Studenten selbst gesammelte Daten, wobei sich jede der 20 Gruppen jeweils einer urbane und einer natürlichen Probestelle à 2m*2m gewidmet hat und 2 Probetage hatte.
Die Daten zur Anzahl der blühenden Pflanzenarten entstanden durch die einfache Zählung der in dem Testbereich aufzufindenden Pflanzen.
Das Aufkommen der Arten wurde durch Bodenfallen (Bodeninvertebraten) und einer zeitlich begrenzten ( 30 min) Zählung des Individuenaufkommens an einer blühenden Pflanze von den Lippenblütler (Bestäuber) bestimmt.
Die Temperatur wurde an beiden Probtagen 3 mal je alle 15 min gemessen und anschließend der Mittelwert berechnet.
Im Nachhinein wurde diese Daten bereinigt und dem Modellierungsziel angepasst.
3.2.2 Lineare Regression
[Bearbeiten]Testet, ob es einen Zusammenhang zwischen einer kontinuierlichen erklärenden Variablen und einer Zielvariable gibt.
Einfache Lineare Regression
Ziel der einfachen linearen Regression ist es, den Wert einer abhängigen Variable (Kriterium) aufgrund einer unabhängigen Variable (Prädiktor) vorherzusagen. Je größer der lineare Zusammenhang zwischen der unabhängigen und der abhängigen Variable ist, desto genauer ist die Vorhersage.

3.2.2.1 P-Wert
[Bearbeiten]Der p-Wert, auch Überschreitungswahrscheinlichkeit oder Signifikanzwert genannt, ist in der Statistik und dort insbesondere in der Testtheorie ein Evidenzmaß für die Glaubwürdigkeit der Nullhypothese, die oft besagt, dass ein bestimmter Zusammenhang nicht besteht.
Fällt beim Vergleich mit dem Signifikanzniveau der p-Wert < 0,05 , dann kann die Nullhypothese ablehnt und dafür die Alternativhypothese H1 angenommen werden.
Überschreitet der p Wert das Signifikanzniveau aber, musst die Nullhypothese vorläufig beibehalten werden.
Berechnen lässt sich der p Wert beispielsweise über allgemein über die z-Transformation und die Normalverteilungstabelle.
z-Transformation
Bei einer z-Transformation werden die Abweichungen der ursprünglichen Werte von ihrem Mittelwert durch ihre Standardabweichung geteilt.
Es wird also berechnet, wie weit der Wert eines Faktors vom Mittelwert der Verteilung entfernt liegt, gemessen in Standardabweichungen, sprich: Standardabweichungs-Einheiten.
Formel:

Normalverteilungstabelle
In der Tabelle der Standardnormalverteilung sind die ersten zwei Ziffern des z-Werts in der ersten Spalte und die zweite Nachkommastelle in der ersten Zeile dargestellt.
Standardabweichung
Formel:
- N - 1 = Anzahl der Freiheitsgrade (gibt an wie viele Werte in einer Berechnungsformel frei variieren dürfen)
- Standardabweichung = √ Varianz
3.2.3 Statistik Programm R
[Bearbeiten]Mit dem Statistikporgramm R kann die Signifikanz zwischen den verschiedenen Faktoren / Ressourcen und der Artenabundanz ermittelt werden. Dabei funktioniert ein p-Wert unter 0,05 als Indikator für einen signifikante Zusammenhang.
Dieser Schritt ist notwendig um bessere Vorhersagen treffen zu können und den Schülern ein Verständis für die beobachteten Ökosysteme und der Arbeit mit statistischen Fragestellungen zu geben.
lm (Abhängige Variable ~ Erklärende Variable)


3.2.3.1 Befehle
[Bearbeiten]Lineare Regression
Testet, ob es einen Zusammenhang zwischen einer kontinuierlichen erklärenden Variablen und einer Zielvariable gibt.
- model_1 <- lm(Zielvariable~Variable, data=Terrestrik)
speichert das Ergebnis des linearen Models (lm) in dem Objekt "model_1"
- summary(model_Tiere)
Der 'summary'-Befehl Zeigt das Ergebnis an.
- Output: Call = Zeigt noch einmal das berechnete Modell.
- Estimate = Steigung (Vorzeichen "-" heißt negativer Zusammenhang, "+" dementsprechend positiver)
- t value = gibt die Testatistik t an (je größer |t| desto eher ist die Regressionsgerade signifikant von Null verschieden, oder in anderen Worten: desto eher gibt, es einen stistischen Zusammenhang)
- P-Wert (= das wichtigste: ist der Zusammenhang signifikant (bei P < 0.05) oder nur Zufall)
Visualsierung mit Streudiagram:
die Regressionsgerade (abline-Befehl) sollte nur bei signifikantem Ergebnis hinzugefügt werden:
- plot(Zielvariable~Urban, data=Terrestrik)
- model_2 <- lm(Zielvariable~Variable, data=Terrestrik)
- summary(model_2)
- plot(Zielvariable~Variable, data=Terrestrik)
- abline(model_2)
Signifikanter Zusammenhang, also mit Regressionsgerade
3.2.4 Ergebnisse
[Bearbeiten]Die lineare Regression ist ein Spezialfall der Regressionsanalyse, also ein statistisches Verfahren, mit dem versucht wird, eine beobachtete abhängige Variable durch eine oder mehrere unabhängige Variablen zu erklären.
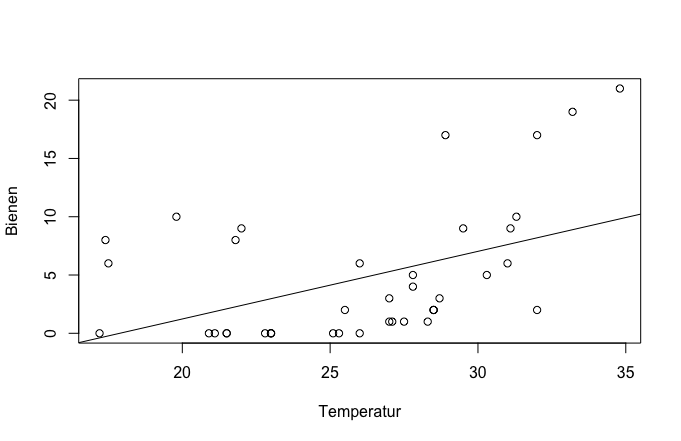
In diesem Fall fungieren die Temperatur und die Anzahl der blühenden Pflanzenarten als erklärende Variablen und die Bienen als abhängige Variable. Für unser Modell muss es eine Signifikanz zwischen der Abundanz der Art und der erklärenden Variable geben.
Interpretation der Ergebnisse:
Die aufgezeigten Plotanalysen veranschaulichen jeweils einen positiven Zusammenhang zwischen den erklärenden Variablen und der Abundanz der Bienen.
Zu beachten ist dabei allerdings, dass die hier aufgezeigten positiven Zusammenhänge nicht für beide erklärenden Variablen unendlich ist.
Während der Anstieg der Temperatur im Intervall von 0°C - 35°C begünstigend auf das Bienenaufkommen wirkt, ist ab einer höheren Temperatur ein rapider Rückgang der Bienenzahl zu erwarten.
Bei einem weiteren Anstieg der blühenden Pflanzenarten ist eine Stagnation in dem Anstieg der Bienenabnundanz zu erwarten.[13]
Eine solche Analyse der erhobenen Daten erleichtert das Verständis für die Zusammenhänge und Wechselwirkungen, welche ein Ökosystem formen.
So können die Faktoren in der Gelände- und Städteplanung berücksichtigt und miteinbezogen werden.
3.2.5 Modellkritik
[Bearbeiten]Dieses Methode zur Veranschaulichung der Ökosystem-Zusammenhänge ist geeignet um eine bestimmte Variable schnell auf ihren Einflussfaktor zu reduzieren und zu analysieren.
Dennoch ist es zur Veranschaulichung der Strukturen innerhalb eines Ökosystems aufgrund dessen Komplexität unzureichend. Um dies zu bewerkstelligen benötigt man zahlreiche Analysen verschiedenster Variabeln und Faktoren zueinder, welche aus einheitlichen Datensätzen stammen müssen. Darunter würde die Übersichtlichkeit der Ergebnisse und möglicher Interpretationen leiden.
Zudem werden nur gegenwärtige Zustände, ohne mögliche Entwicklungen der Zusammenhänge (postiv/negativ) beschrieben. Somit können nur die momentanen Realitätswerte aufgezeigt werden und es wird kein Blick über die Werte hinaus ermöglicht.
Dessen unbeachtet handelt es sich um ein gutes Tool um die Biodiversität und ihre unterstützenden bzw. gegenwirkenden Faktoren in kommende Inverstitions - bzw. Stadtplanungsentscheidungen einzubeziehen.
3.3. Modellierungszyklus 3 – Niveau Universität
[Bearbeiten]3.3.1 Vorstellung Simpson-Diversitätsindex
[Bearbeiten]
Der von Edward H. Simpson 1949 entwickelte Simpson-Index dient zu Beschreibung der Biodiversität. Die Biodiversität wird hier dadurch beschrieben, dass man errechnet wie wahrscheinlich es ist, dass zwei zufällig ausgewählte Individuen aus einer Probestelle nicht der gleichen Art angehören. Zur Berechnung wird die Wahrscheinlichkeit ausgerechnet, eine bestimmte bestimmte Art „zu ziehen“ und die gleiche Art dann erneut „zu ziehen“. Wobei es sich hier um „Ziehen ohne Zurücklegen“ handelt, da man das erste Individuum nicht mehr ziehen kann. Anschließend wird dieses Produkt für alle Arten summiert. Da man jetzt ausgerechnet hat, wie wahrscheinlich es ist zweimal die selbe Art zu ziehen muss man voran „1-“ stellen, um die Gegenwahrscheinlichkeit davon auszurechen. Das Ergebnis beschreibt die Wahrscheinlichkeit, mit der zwei ausgewählte Individuen nicht der selben Art angehören.
D ist 0, wenn es nur eine Art in dem Habitat gibt und folglich alle Individuen dieser Art angehören. Je größer die Diversität ist, desto näher kommt d der 1. Werte nah an 1 sind zu erwarten, wenn es viele verschiedene Arten gibt oder wenn alle vorkommenden Arten sehr ausgeglichene Abundanzen haben, die Biodiversität ist in diesem Fall hoch.
3.3.2 Probestellen
[Bearbeiten]Zur Festlegung der Streumaße für die 40 Formeln zur Darstellung der Bioviversität an den Probestellen haben wir die Standorte in Klein, Mittel und Groß untergliedert.
- Klein: Straßeninseln, Gärten etc.
- Mittel: Parks, mittelgroße urbane Grünflächen etc.
- Groß: Felder, Wälder etc.
Das Streumaß beschreibt für welchen Radius die erhobenen Messwerte übereinstimmen. (konzentrische Kreise)
So gelten die auf einer Straßeninsel erhobenen Daten nur für diesen sehr eingeschrenkten Bereich, während die auf einem Feld erhobenen Daten vermutlich mit den Werten des ganzen Feldes korrelieren und übereinstimmen.
Bei den hier festgelegten Streumaßen handelt es sich nur um Schätzungen und wir erheben keinen Anspruch auf konkrete Richtigkeit. Vielmehr möchten wir die Komplexität der Ökosysteme durch den addierten Faktor des Streumaßes aufzeigen und miteinbeziehen.
3.3.3 Grenzen der Software
[Bearbeiten]Unsere Visualisierung über CAS und Maxima sind an ihre Grenzen gekommen, da die Datenmenge beide Programme überfordert hat. Die Daten der 41 Probestellen hat die Programme vor allem durch die Angaben der Längen- und Breitengrade überfordert. Diese großen Dezimalzahlen mussten wir in unseren Formeln als Bruch darstellen und dabei entstanden Numerikfehler bei der Diskretisierung .
Da wir uns mit unserer Modellbildung nur im Raum Landau und Nahen Umfeld aufgehalten haben liegen die Koordinaten sehr nah beieinander. So hat die ursprüngliche Darstellung der Daten in den Computeralgebrasystemen nicht funktioniert die Peaks lagen zu nah beieinander und wurde so nur als ein Peak dargestellt.
In Maxima wurden zusätzlich auch die Werte der Z-Kooridnate addiert, da die x- und y- Werte so nah beieinander lagen, dass diese nur als ein Punkt im Koordinatensystem interpretiert wurden.
Auch das Streumaß, welches eigentlich zur Darstellung der Größe der Probefläche dienen soll, musste mehrfach angepasst werden, da auch schon eine Streuung von 1 um die Koordinaten deutlich zu groß war und keine Unterscheidung mehr sichtbar war. Viele der aufgetretenen Probleme liegen an den numerischen Methoden dahinter. Durch das abstrahieren unserer Daten und gerade der langen Bruchangaben durch die Längen- und Breitengrade, die auch noch räumlich sehr nah beieinander liegen, geht die Genauigkeit unserer sonst richtig aufgestellten Formeln zur Beschreibung der Biodiversitätskarten verloren. Durch diese Numerikfehler lassen sich unsere Daten ohne Anpassung nicht wie von uns gewünscht darstellen.

CAS4Wiki:
Maxima:

3.3.4 Lösungsansätze
[Bearbeiten]Karte mit veränderte Werte (Koordinaten, Streumaß, Diversitätsindex etc.)

Lösungsansätze:
- Längen- und Breitengrad anpassen
- Streumaße anpassen
- Nicht so viele Daten in Programm einlesen (Reduktion auf 4 Funktionen)
- Georeferenzierungs Programme nutzen da diese für Längen- und Breitengrade ausgelegt sind und damit umgehen können z.B. qGIS
3.3.5 Diversitätskarten Beispielhaft
[Bearbeiten]3.3.6 Modellkritik und Ausblick
[Bearbeiten]Maxima und CAS4Wiki bieten gute Werkzeuge um Funktionen in mehreren Dimensionen zu veranschaulichen.
Geogebra 3D Rechner war ebenfalls mit Datenmenge überfordert.
Voraussetzung für die Nutzung sind exakte Brüche und sich nicht zu eng überschneidende Daten. Dies steht im Widerspruch mit dem Einbezug von Koordinaten aus einem relativ kleinen Testungsgebiet.
Zudem sind die Programme nicht für die Darstellung großer Datensätze gemacht.
Somit sind die Software von Maxima als auch von CAS4Wiki mit unserem ursprünglichen Modellierungsanspruch an ihre Grenzen gekommen.
Maxima nicht für alle Systemlaufwerke (z.B. MacOS) möglich
Unsere Modellierung könnte man auch erweitern mit anderen Programmen visualisieren, wie zum Beispiel qGIS. Da dieses Programm vor allem auch einen Platz in der Geographie findet, könnte man gerade hier die geographische Darstellung thematisieren und mit Georeferenzierung arbeiten.
Unsere Modellierung soll auch für andere Daten und Modellierungsziele nutzbar sein und es sollen verschiedene Datensätze eingelesen werden können.
4.Softwarenutzung
[Bearbeiten]Welche Software wurde/wird in Ihrem Projekt für die Modellierung eingesetzt und welche Funktion hat diese für Sie?
Sek 1: Tabellenkalkulation
Sek 2: Statistikprogramm R
Uni-Niveau: Tabellenkalkulation, Maxima/CAS
5.Quellen
[Bearbeiten]- ↑ https://www.leopoldina.org/themen/biodiversitaet/warum-artenvielfalt/
- ↑ https://www.de-ipbes.de/de/Globales-IPBES-Assessment-zu-Biodiversitat-und-Okosystemleistungen-1934.html
- ↑ https://www.de-ipbes.de/de/Globales-IPBES-Assessment-zu-Biodiversitat-und-Okosystemleistungen-1934.html
- ↑ [2]
- ↑ [3]
- ↑ [https://www.millenniumassessment.org/documents/document.300.aspx.pdf
- ↑ https://www.bundesregierung.de/breg-de/themen/nachhaltigkeitspolitik/nachhaltigkeitsziele-erklaert-232174
- ↑ https://17ziele.de/ziele/13.html
- ↑ https://17ziele.de/ziele/15.html
- ↑ https://17ziele.de/ziele/6.html
- ↑ https://www.duden.de/rechtschreibung/Diversitaet
- ↑ https://www.umweltbundesamt.de/das-uba/was-wir-tun/forschen/umwelt-beobachten/biodiversitaet#umweltschutz-und-biodiversitat
- ↑ https://link.springer.com/article/10.1007/BF00339537#Abs1,











![{\displaystyle {}plot3d(a(x,y),b(x,y),c(x,y),d(x,y),x[49.2,50],y[7,9]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaafb0996e2f826c828ffd31866ccde145be7f41)



