Kurs:Mathematische Modellbildung/Themen/Biodiversität/Einführung

Einleitung

Text

• Erster Pinlkt
• Zweiter Puzbnkt

Warum Biodiversität?

Biodiversität = Vielfalt aller lebenden Organismen, Lebensräume und Ökosysteme auf dem Land, im Süßwasser, in den Ozeanen und in der Luft

• Stabilität der Ökosysteme
• Versorgungsleistungen
• Regulierende Leistungen
• Kulturelle Leistungen
• Unterstützende Leistungen

Sustainable Development Goals

Abbildung 1: Sustainable Development Goals

Direkte Verbindung:

• 13 „Maßnahmen zum Klimaschutz“, 14 „Leben unter Wasser“ und 15 „Leben an Land“

Indirekte Verbindung:

• 3 „Gesundheit und Wohlergehen“, 6 „Sauberes Wasser und Sanitäreinrichtungen“ und 12 „Nachhaltige/r Konsum und Produktion“

Ziel der Modellbildung und Zielgruppen

Ziel: Entscheidungsvorgänge bezüglich des Flächenmanagements einfacher gestalten

• Betrachtung und Visualisierung von Biodiversitätshotspots

Zielgruppen:

• NGOs
• Naturschutzorganisationen & -behörden
• Ökologisch orientierte Unternehmen

All diese Nutzergruppen sollen durch unsere Modellierungsergebnisse besser basierte Entscheidungen für die Finanzierung von Naturschutz treffen können.

Modellierungszyklus 1 - Niveau Sekundarstufe 1

• Artenreichtum = Artenvielfalt die Anzahl von verschiedenen Arten an einem Ort
• Limitationen im Vergleich der Diversitäten verschiedener Artgemeinschaften, deshalb wurden weitere Maße entwickelt

* Alpha-Diversität = Anzahl der Arten in einem bestimmten Habitat oder einer Gemeinschaft (Artenzahl in bestimmten Ökosystem vergleichen)
* zwischen zwei oder mehr Habitaten vergleichenbar

* Gamma-Diversität = Artzahl in eine großen Region (sehr diverse Landschaften oder größere geographische Skalen, z.B. große Steppe/Prärie USA) 
* Alpha- und Gamma-Diversität = inventaresche Diversität

* Beta-Diversität = Änderung der Artzusammensetzung entlang ökologischen oder geographischen Gradienten
* die Beta-Diversität ist hoch, wenn die Artzusammensetzung sehr verschieden ist
* Differenzierungsdiversität

• die unterschiedlichen Diversitäten haben unterschiedliche Aussagekraft über die tatsächliche Biodiversität eines Raumes

Datenerstellung

• drei Regionen, die aus jeweils drei Bergen bestehen
• die Artzusammensetzung variiert von Berg zu Berg
• Region 1 große Überschneidung, Region 3 kaum Überschneidung

Berechnung der Diversitäten

Alpha-Diversität:

• ein Habitat Anzahl = der Arten der Artgemeinschaft zählen (Summe der vorkommenden Arten)
• zwischen zwei oder mehr Habitaten = Mittelwert der Artenzahl aus der Anzahl der Regionen

Bild Formel Mittelwert

a=Anzahl der Arten pro Berg

n=Anzahl der Berge

Gamma-Diversität:

• Summe der Arten einer Region, es darf sich keine Art überschneiden

Beta-Diversität:

• errechnet man aus den anderen zwei Diversitäten
• Beta = Gamma / mittlere Alpha
• im Beispiel Beta=1,17, da 7/6=1,17
• Beta-Diversität ist dann sehr hoch, wenn sehr unterschiedliche Artzusammensetzungen von Habitat zu Habitat in der Region vorkommen

Tabellenkalkulation

Genutzt Befehle und unsere Vorgehensweise:

• die Artzahlen und - Zusammensetzungen wurden von uns frei gewählt und absichtlich in einem kleinen Zahlenraum belassen
• zur Berechnung der Alpha-Diversität wurde =MITTELWERT() genutzt
• die Gamma-D kann anhand unseres Schaubilds abgelesen werden, hierfür wird die Summe der sich nicht überschneidenden Arten genommen
• die Beta-Diversität wurde mit =γ/α berechnet
• die Zellen wurden für die Übersichtlichkeit mit zwei Nachkommastellen formatiert

Ergebnisinterpretation

• die Ergebnisse geben sehr verschiedene Eindrücke wieder

* Alpha-Diversität: Artenreichtum eines Habitats/einer Region
* Beta-Diversität: Differenzierung der Artenzusammensetzung einer Region
* Gamma-Diversität: Artenreichtum eines größeren Gebiets

• man muss differenzieren welche Diversität man betrachten will

Modellkritik

Text

• Erster Pinlkt
• Zweiter Puzbnkt

Modellierungszyklus 2 - Niveau Sekundarstufe II

Wie hängen die Ressourcen und die Artenzahl miteinander zusammen?

Datenvorstellung Screenshot Tabelle bereinigte mit Koordinaten

• Signifikanz geprüft und Daten bereinigen
• Daten dem Modellierungsziel angepasst

Lineare Regression

• Zusammenhang zwischen einer kontinuierlichen erklärenden Variablen und einer Zielvariable

Einfache Lineare Regression
Ziel: Wert einer abhängigen Variable aufgrund einer unabhängigen Variable vorherzusagen.
Je größer der lineare Zusammenhang zwischen der unabhängigen und der abhängigen Variable ist, desto genauer ist die Vorhersage.
'

Lineare Regression - T-Wert

t-Wert: berechnete Größe der Differenz relativ zur Streuung in den Stichprobendaten, dargestellt in Einheiten des Standardfehlers ( Werte - Tabelle)
→ Je größer der Betrag von t ist, umso stärker spricht dies gegen die Nullhypothese.

H0: Es besteht kein signifikanter Zusammenhang
H1: Es besteht ein signifikanter Zusammenhang

Ermittlung des P-Werts

P-Wert:Evidenzmaß für die Glaubwürdigkeit der Nullhypothese
Berechnung:

• über die Wahrscheinlichkeitsfunktion der Binomialverteilung
  
• allgemein über die z-Transformation und die Normalverteilungstabelle.
  

Z- Wert: Abweichungen der ursprünglichen Werte von ihrem Mittelwert geteilt durch ihre Standardabweichung -> Wie weit liegt der Wert eines Faktors vom Mittelwert der Verteilung entfernt?

Ermittlung des P-Werts

Standardabweichung:

• N - 1 = Anzahl der Freiheitsgrade (gibt an wie viele Werte in einer Berechnungsformel frei variieren dürfen)
• Standardabweichung = √ Varianz

Ermittlung des P-Werts

Normalverteilungstabelle

Statistik-Programm R

• Signifikanz zwischen den verschiedenen Faktoren / Ressourcen und der Artenabundanz ermittelt
• p-Wert unter 0,05 Indikator für einen signifikante Zusammenhang

lm (Abhängige Variable ~ Erklärende Variable)

Statistik-Programm R

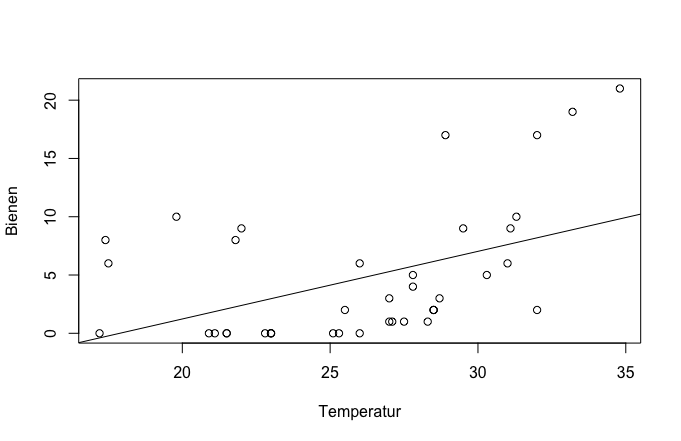
• Temperatur und die Anzahl der blühenden Pflanzenarten als erklärende Variablen und die Bienen als abhängige Variable
• Signifikanz zwischen der Abundanz der Art und der erklärenden Variable für Modell notwendig

Modellierungszyklus 2 - Modellkritik

• geeignet, um eine bestimmte Variable schnell auf ihren Einflussfaktor zu reduzieren und zu analysieren.
• zur Veranschaulichung der Strukturen innerhalb eines Ökosystems aufgrund dessen Komplexität unzureichend

→ zahlreiche Analysen verschiedenster Variablen und Faktoren zueinander, welche aus einheitlichen Datensätzen stammen notwendig

• nur gegenwärtige Zustände, ohne mögliche Entwicklungen der Zusammenhänge (positiv / negativ) beschrieben.

→ dennoch gutes Tool um die Biodiversität und ihre unterstützenden bzw. entgegenwirkenden Faktoren in kommende Investitions - bzw. Stadtplanungsentscheidungen einzubeziehen.

Modellierungszyklus 3 – Niveau Universität

Simpson - Index: Wie wahrscheinlich ist es, dass zwei zufällig ausgewählte Individuen aus einer Probestelle nicht der gleichen Art angehören?

Probestellen

Modellierungszyklus 3 - Grenzen der Software

a(x,y):=1/(1+((x-(49+50599/250000))^2+(y-(8+94237/1000000))^2)/(2/1000))
b(x,y):=1/(1+((x-(49+12669/62500))^2+(y-(8+127374/1000000))^2)/(2/1000))
c(x,y):=1/(1+((x-(49+2079513/10000000))^2+(y-(8+84061/1000000))^2)/(6/1000))
d(x,y):=1/(1+((x-(49+1889727/10000000))^2+(y-(8+602529/5000000))^2)/(1/100))

CAS4Wiki:
plot3d(a(x,y),b(x,y),c(x,y),d(x,y),x[49.2,50],y[7,9])

Modellierungszyklus 3 - Grenzen der Software

Maxima:

Lösungsansätze

Karte mit veränderte Werte (Koordinaten, Streumaß, Diversitätsindex etc.)

Lösungsansätze:

• Längen- und Breitengrad anpassen
• Streumaße anpassen
• Nicht so viele Daten in Programm einlesen (Reduktion auf 4 Funktionen)
• Georeferenzierungs Programme nutzen da diese für Längen- und Breitengrade ausgelegt sind und damit umgehen können z.B. qGIS

Diversitätskarte

Modellkritik und Ausblick

Sek 1: Tabellenkalkulation
Sek 2: Statistikprogramm R
Uni-Niveau: Tabellenkalkulation, Maxima/CAS