Kurs:Mathematische Modellbildung/Themen/Energiekosten/Modellierungszyklus - Sek II

Modellierung des Wärmerverlusts aufgrund der Bauweise eines Hallenschwimmbades

Im Modellierungszyklus 1 wurde das Hauptaugenmerk auf die Kosten für die Beschaffung des Wassers und dessen Erwärmung gelegt. Nun ist es so, dass auch die Halle an sich beheizt werden muss. Es findet aufgrund der Temperaturdifferenz zwischen Halle und Außenbereich ein ständiger Energiefluss in Form von Wärme von innen nach außen statt. Dieser muss durch das Heizen der Halle ständig ausgeglichen werden. Bei den meisten Hallenschwimmbädern bilden Glasflächen den Großteil der Außenwand. Der Wärmeaustausch soll hier durch folgende Formel beschrieben werden:

Formel[Bearbeiten]

$(1)E=k\cdot A\cdot {\frac {T1-T2}{d}}$

E ist der momentane Wärmeverlust pro Sekunde

Erläuterung[Bearbeiten]

Hierbei steht E für die momentane Energieabgabe pro Sekunde (da physikalische Formeln auf SI Einheiten genormt sind). Wollte man also die Energieabgabe in einer bestimmten Periode berechnen, müsste man den erhaltenen Wert mit der gewünschten Zeit in Sekunden multiplizieren. Mathematisch gesehen, stellt diese Gleichung also die momentane Energieabgabe dar. Ferner steht k für den Wärmeleitungskoeffizient des verwendeten Materials, A für die Fläche durch die die Wärme abgegeben wird, T1 (außen) und T2 (innen) für die Temperaturdifferenz zwischen Halle und Außenbereich und d für die Dicke der Glasscheibe durch die die Wärme abfließt.

Da sich nun die Außentemperatur im Laufe des Tages ändert, ändert sich dementsprechend auch die Temperaturdifferenz. Wir wollen nun untersuchen, welche Auswirkungen ein späteres Öffnen des Schwimmbades auf den Energieverbrauch der Heizung hätte.

Wir wollen infolgedessen davon ausgehen, dass das Schwimmabd anstatt um 7 Uhr morgens erst um 9 Uhr seine Pforten öffnet. Es muss demnach weniger geheizt werden. Den Anstieg der Temperatur in diesen zwei Stunden wollen wir durch eine Exponentialfunktion modellieren. Eine lineare Funktion würde diesen Verlauf nur annähernd beschreiben, da sich der Temperaturverlauf eines Tages zu dieser Uhrzeit exponentiell darstellt. Folgender Ansatz wird gewählt:

$(2)f(t)=c\cdot a^{t/3600}$

mit t in Sekunden ab 7 Uhr morgens

Selbstverständlich wird hier der Temperaturverlauf eines Wintertages betrachtet. In Karlsruhe wurde Stand heute eine Temperatur von 3°C um 7 Uhr gemessen. Um 9 Uhr waren es bereits 6°C. Diese beiden Wertepaar sollen die Grundlage für die Modellierung dieser Exponentialfunktion darstellen. Der Startwert c wird also für 7 Uhr morgens mit 3°C eingetragen. Der Wachstumsfaktor a wird berechnet, indem das Wertepaar (7200/6) in die Ursprungsformel eingetragen und nach a umgestellt wird. Es ergibt ich als dann in Wert von a=1,41. Aufgrund dieser beider Daten wird die Funktion nun zu:

$(3)f(t)=3\cdot 1,41^{t/3600}$

Erreicht wurde nun ein funktionaler Zusammenhang von Uhrzeit und Außentemperatur zwischen 7 und 9 Uhr morgens. Betrachtet man nun wieder die Funktion der momentanen Energieänderungen, wird deutlich dass dies in T1 eingesetzt werden kann. Somit wird der Wert für T1 zu einer variablen Größe. Geht man davon aus, dass die Innentemperatur des Hallenbades auf ca. 28°C gehalten werden soll, k für eine normale Glasscheibe bei ca. 0,76 liegt, die Dicke der Glasscheibe mit 0,02m angenommen wird und man die Fläche auf einen Quadratmeter normiert stellt dies die einzige Veränderliche dar. Eingesetzt in Formel (1) ergäbe dies folgenden Zusammenhang:

$(4)E(t)=0,76\cdot 1\cdot {\frac {3\cdot 1,41^{t/3600}-28}{0,02}}$

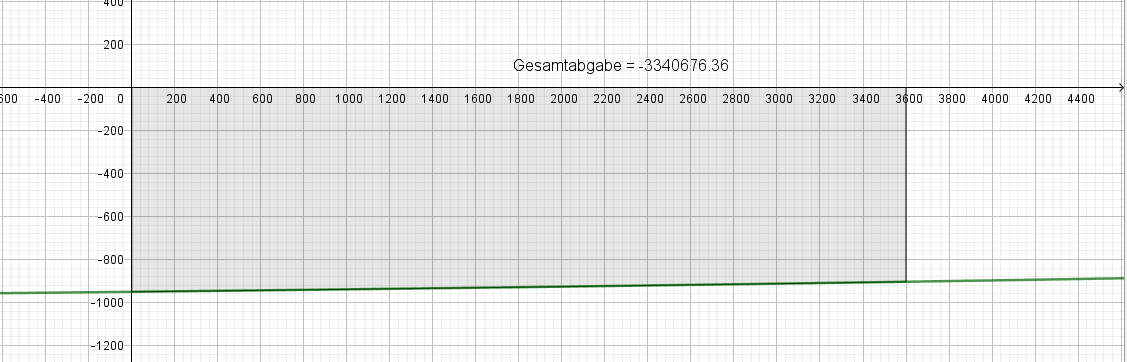
Wir erreichen somit einen funktionalen Zusammenhang zwischen der momentanen Energieabgabe und der Uhrzeit. Physikalisch gesehen sprechen wir hier quasi von der Ableitung der Gesamtenergiefunktion. Im Folgenden wollen wir mithilfe der Integralrechnung die gesamte abgegebene Energiemenge in diesem Zeitraum berechnen. Dies lässt sich übr die Integration über die beiden ersten Öffnungsstunden erreichen. In Geogebra lässt sich dies einfach berechnen wie im Bild links zu sehen. Die Stammfunktion errechnet sich mithilfe Maxima zu : $F(t)=38\cdot {\frac {31432,84\cdot 1,41^{(t/3600)}-28}{0,02}}$

Mithilfe von Geogebra lässt sich nun das Integral von 0 bis 2 berechnen. Dieser Wert stellt die abgegebene Energiemenge in diesen beiden Stunden pro Quadratmer Fensterfläche dar.

Wie anhand der Grafik zu sehen, gehen in diesen beiden ersten Stunden nach Eröffnung rund 3340 kW durch einen Quadratmeter Fensterfläche verloren. Dies ist hochgerechnet auf die Gesamtglasfläche eines Schwimmbads sehr erheblich.

Mögliche Lösungen Energie zu sparen könnten eine dickere Fensterscheibe sein (eventuell auch Doppelverglasung oder Dreifachverglasung), die Innentemperatur so niedrig wie möglich zu halten um das Delta zu verringern oder einfach Glasflächen durch Beton oder Mauerwerk zu ersetzen. Allerdings hätte dies zur Folge, dass sich diese Investition erst amortisieren müsste. Bei einer verringerten Öffnungszeit hätte man direkt Einsparungen in Energie und auch bzgl. der Personalkosten.

Seiteninformation[Bearbeiten]

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal[Bearbeiten]

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Mathematische Modellbildung' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Mathematische%20Modellbildung/Themen/Energiekosten/Modellierungszyklus%20-%20Sek%20II
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.