Kurs:Mathematische Modellbildung/Themen/Perfekter Freistoß/Zyklus 1
Erscheinungsbild
Zyklus 1: (Niveau Sekundarstufe 1)
[Bearbeiten]Vorgehen
[Bearbeiten]Ziel: Ermittlung der optimalen Höhe an der Mauer um Handlungsempfehlungen an den Schützen zu geben.
- Ausgehen von einem Spannschuss (lineare Funktion der Form f(x)=ax+b)
- näherungsweise (maschinelles) Annähern an "die perfekte Ballhöhe über der Mauer"
- Aufteilen in zwei lineare Funktionen
perfekte Freistoßkurve als lineare Funktionen
[Bearbeiten]
Berechnung (1)
[Bearbeiten]- Berechnung der Funktion des Spannschusses anhand der gegebenen Punkte (0/2.24) und (16/0)
- f(x)= -0,14x + 2,24
- Deuten des Ergebnisses: Ball überwindet Mauer nicht
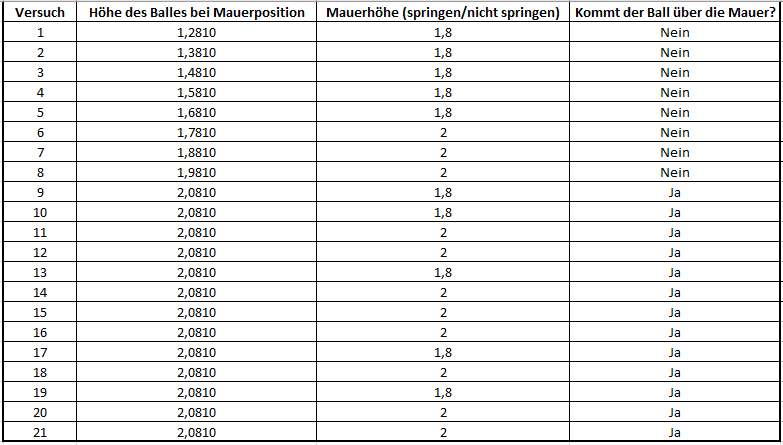
- Benutzen einer Schritttweite als Handlungsempfehlung für den Schützen (10cm)
- Handlungsempfehlung wird so lange ausgeführt, bis der Ball die Mauer überwindet (egal ob Mauer springt oder nicht), ca. 2,1m
Berechnung (2)
[Bearbeiten]- Einteilung in zwei lineare Funktionen
- Berechnen der linearen Funktionen
- 1. Funktion Freistoßpositon-Mauer: f(x)=-0,23x+3,68
- 2. Funktion Mauer bis Tor f(x)=-0,02x+2,24
perfekte Höhe des Balles bei Mauerposition
[Bearbeiten]
Ergebnisse
[Bearbeiten]- Höhe des Balles bei Mauer (2,1m)
- Spannschuss geht über das Tor bei optimaler Höhe an der Mauer
- Einteilung in Teilfunktionen, allerdings realitätsfern
- Daher Zyklus 2