Kurs:Mathematische Modellbildung/Themen/Perfekter Freistoß

Anmerkungen (AH) 05.02.2024

Dies ist ein altes Modellierungsportfolio. Sind im WS 2023/24 neue Inhalte dazugekommen? Wenn nicht, welchen Beitrag haben die Gruppenteilnehmer des aktuellen Semester hierzu geleistet?

Das Modell wurde im WS22/23 von allen vier Mitgliedern erstellt und im SS23 ebenfalls von allen zusammen überarbeitet. Im WS 23/24 wurden einige Erklärungen und Definitionen von Gruppenteilnehmer (Nr.4) erneut überarbeitet. Ebenso wurden Aufgaben des aktuellen Semesters hinzugefügt. Mathematische Berechnungen und Darstellungen wurden allerdings nicht verändert.

Bitte ergänzen Sie die zusammensetzung der Gruppe, s.u.

Die Zusammensetzung der Mitglieder wurde ergänzt.

Modellierungsthema und Zielsetzung

Modellierungsthema

Hier entsteht ein Portfolio zur Mathematischen Modellbildung zum Thema:
Der perfekte Freistoß
In der hier durchgeführten Modellierung geht es um die Frage, wie muss ein Freistoß ausgeführt werden, sodass der Ball in den oberen Winkel des Tores fliegt? Inwiefern ist es möglich, eine perfekte Freistoßkurve im Fußball mathematisch zu modellieren und auszuwerten? Kann man mit der Modellierung eine Auswertung erstellen um für eine Zielgruppe eine Art Lerneffekt zu erzielen?

Gruppenteilnehmer

1. Bastian Ottmann (SS23)
2. Pelle Pézsa (SS23)
3. Felix Mayer (SS23)
4. Lisa Glaub (WS23/24)

Definition - (perfekter) Freistoß

Im Fußball versteht man unter einem Freistoß einen Spielzug, der nach einem Regelverstoß der gegnerischen Mannschaft ausgeführt wird.
Regelverstöße sind Fouls jeglicher Art, allerdings können Schiedsrichter auch Unsportlichkeiten mit Freistößen bestrafen.
Bei einem Freistoß hat ein Spieler die Aufgabe, den auf dem Rasen ruhenden Ball von der gefoulten Stelle in das Tor zu befördern.
Hierbei darf die gegnerische Mannschaft nicht näher als 9,15 Meter an den Ball heran kommen. Sie hat allerdings die Möglichkeit Spieler an dieser Entfernungsmarke zu positionieren, um eine sogenannte "Mauer" zu bilden. So wird der Freistoß für den Schützen erschwert. Ebenso steht der Torwart des gegnerischen Teams im Tor und kann versuchen den Ball abwehren.
Es gibt zwei Arten von Freistößen - den direkten und den indirekten Freistoß.
Beim "indirekten Freistoß" muss der Ball von einem Mitspieler berührt werden, bevor er ins Tor geschossen werden darf.
Beim "direkten Freistoß" ist dies nicht nötig - der erste Ballkontakt kann somit unmittelbar zu einem Tor führen.
Es gibt diverse Varianten, einen Freistoß zu schießen.
Entscheidend ist hierbei unter anderem die Schusstechnik. Beim direkten Freistoß wird meist mit dem Rist, mit Effét oder Vollspann geschossen.
In unserem Modell werden wir uns die Variante des direkten Freistoßes genauer anschauen.
Des Weiteren definieren wir einen "perfekten Freistoß" als einen Schuss eines Spielers über eine Mauer, der im oberen, linken oder rechten Winkel des Tores landet.

Voraussetzungen

Grundannahmen

Grundannahmen sind Voraussetzungen, welche nicht verändert werden können. Hier legen wir also unsere Parameter für die Modellierung fest.

Bei unserer Modellierung gehen wir von einem Bundesliga Spielfeld mit den Standardmaßen von 68m x 105m aus.
Das Tor hat eine Breite von 7,32 Metern und eine Höhe von 2,44 Metern.
Die Distanz der Ausführungsmarke unseres gewählten Freistoßes bis zum Tor beträgt 16 Meter und befindet sich mittig davor.
Bälle der Bundesliga haben einen Durchmesser von 20cm. Dies entspircht der Ballgröße 5.
Falls der Ball direkt in einen der oberen Winkel geht, so sprechen wir von einem Tor. Direkt bedeutet, dass der Ball weder Mauer noch Pfosten oder andere Hindernisse berührt. Da wir in unserem Modell lediglich den "direkten Freistoß" betrachten, sehen wir ebenfalls vom Ballkontakt der eigenen Mitspieler ab.

Externe Faktoren

Externe Faktoren sind nicht vom Freistoßschützen veränderbar. Allerdings können diese je nach Situation und Gegner variieren, manche sind aber auch fest gesetzt und somit unveränderbar.

Die Distanz von der Ausführungsmarke unseres gewählten Freistoßes bis zur Mauer darf nicht weniger als 9,15 Meter betragen.
Die Mauerhöhe ist unter anderem abhängig von den jeweiligen Körpergrößen der Gegenspieler. Allerdings gehen wir in unserem Modell von der durchschnittlichen Größe eines Mannes in Deutschland aus, also von 1,80 Metern.
Außerdem nehmen wir an, dass die Mauer aus fünf Spielern besteht, die alle gleich groß sind.
Da "die Mauer" auch springen kann und wir von einer durchschnittlichen Sprunghöhe von zusätzlichen 20cm ausgehen, kann die Mauer also eine Höhe von 1,80 Metern bis maximal 2 Metern haben.
Die Stellung des Torwarts im Tor entscheidet ebenfalls über das Gelingen des Freistoßes. Versucht der Freistoßschütze in die oberen Ecken des Tores zu treffen, hat der Torwart, der ebenfalls 1,80 Meter groß ist, "schlechtere Chancen" an den Ball zu kommen.
Witterungen wie beispielsweise Regen, Schnee oder Sturm beeinflussen das Spielgeschehen deutlich. Je nachdem muss der Schütze zusätzliche Überlegungen für den Schuss treffen. Bei heftigem Wind spielen zum Beispiel Windrichtung und Windstärke eine wichtige Rolle.

Interne Faktoren

Interne Faktoren sind von dem Freistoßschützen abhängig.
So kann dieser je nach seiner persönlichen Einschätzung Anpassungen an seiner Schusstechnik vornehmen, um den Ball mit einer höheren Wahrscheinlichkeit in das Tor zu treffen.

Die Qualität des Schusses eines jeden Spielers hängt von mehreren Faktoren ab.
So kann der Ball beispielsweise in verschiedene Richtungen gelenkt werden, je nachdem wie der Freistoßschütze den Ball spielt. Zum Einen liegt der Fokus eines Vollspannschusses auf der Schussstärke, allerdings kann die Präzision darunter leiden. Zum Anderen hat der Ball bei einem Effétschuss keine lineare Flugbahn.
Des Weiteren spielt es eine Rolle, ob der Schütze mit links oder rechts schießt.
Es kommt nicht nur darauf an, wie der Freistoßschütze den Ball mit dem Fuß berührt, sondern ebenfalls wo der Ball damit getroffen wird. Ob der Ball mittig, oben oder unten getroffen wird, bestimmt ebenfalls seine Flugbahn.
Falls der Schütze Anlauf nimmt, ändert dies ebenfalls die Flugbahn des Balles, da die Schussstärke variiert.

________________________________________________________________________________________

Dies sind die Faktoren die wir in unserer Modellierung beachten.
Natürlich spielen weitere Faktoren, wie die Länge des Beines des Freistoßschützen oder die individuellen Torwartfähigkeiten, Reflexe und Reaktion ebenfalls eine Rolle bei der Ermittlung des perfekten Freistoßschusses. Jedoch werden diese und andere bei unseren Modellierungszyklen außer Acht gelassen.

Modellierungsziel

Welche Bedingungen muss ein Freistoß erfüllen, um dem perfekten Freistoß möglichst nah zu kommen?
Wie lassen sich Handlungsempfehlungen an den Schützen formulieren?
Lassen sich anhand dieser mathematisch modellierten Profile weitere Erkenntnisse analysieren?

Nutzergruppe

Mit Hilfe unserer Modellierung können fortgeschrittene Fußballspieler ihre Freistoßtechnik analysieren und somit verbessern. Aber auch Freizeitsportler bekommen mit unserem Modell einen ersten Einblick in ihre Leistungen und sehen von Beginn an an welchen Techniken und Fähigkeiten sie arbeiten müssen, um besser zu werden.

Softwarenutzung

Welche Software wird in Ihrem Projekt für die Modellierung eingesetzt und welche Funktion hat diese für Sie?

Wir benutzen folgende Software:

• Tabellenkalkulation - Damit erstellen wir unsere Datensätze und werten diese aus

• Geogebra - Dient zur Veranschaulichung der mathematischen Strukturen

• wxMaxima - Benutzen wir zur Berechnung der Datensätze

Zuordnung des Modellierungsthemas zu den UN-Nachhaltigkeitszielen [1]

Durch unsere Modellierung im Rahmen des Kurses „Mathematische Modellierung“ wollen wir uns am Nachhaltigkeitsprozess beteiligen. Denn dem Fußball aber auch Sportarten im Allgemeinen kann eine Entwicklungsaufgabe im Sinne der Nachhaltigkeit zugeschrieben werden. Gesundheit, Bildung und soziale Integration des Einzelnen sowie der gesamten Gemeinschaften können durch Förderung von Werten wie Gleichberechtigung, Toleranz, Fairness und Respekt gestärkt und gefestigt werden.

Die in der UN-Agenda „Transforming Our World: Agenda 2030 for Sustainable Development“ aufgeführten Ziele für eine nachhaltige Entwicklung können dabei mit Sport in Verbindung gebracht und somit mit unserem mathematischen Modell verknüpft werden.

• SDG3: Good Health and Well-being:
• SDG5: Gender Equality
• SDG10: Reduced Inequalities
• SDG16: Peace, Justice and Strong Institutions
• SDG17: Partnerships for the Goals

Niveauzuordnung

Niveau Sekundarstufe 1

• Flugbahn durch lineare Funktionen darstellen
• die optimale Höhe des Balles an der Mauerposition mittels Tabellenkalkulation bestimmen

Niveau Sekundarstufe 2

• durch maschinelles Lernen aus Zyklus 1: passendere Strukturen für die Modellierung erkennen
• Flugbahn durch quadratische Funktion darstellen
• Lineare Algebra anwenden um Gleichungssysteme zu lösen
• Kurvendiskussion und Annähern an die perfekte quadratische Funktion durch Integralberechnung und Matritzen.

Niveau Universität

• Wahrscheinlichkeitsdichte
• Schussprofil erstellen

Modellierungszyklen

Zyklus 1: (Niveau Sekundarstufe 1)

In unserem ersten Zyklus betrachten wir die Freistoßkurve als Verknüpfung mehrerer linearer Funktionen. Diese werden durch die Formel f(x)=ax+b bestimmt.
Der Ausgangspunkt, an dem der Freistoß ausgeführt wird, befindet sich genau 16 Meter von dem Tor entfernt und der Ball liegt ruhend auf dem Rasen.
So ergibt sich ein erster fester Punkt (16/0).
Das Tor, in das der Schütze bestenfalls schießen soll, hat eine Höhe von 2,44m. Damit der Fußball in das Tor geht, sollte aufgrund des Ball-Durchmessers die Unterkante des Balles auf der Höhe der Mauer bei 2,10m sein. 9,15 m von der Freistoßmarke entfernt, befindet sich die gegnerische Mauer. So liegt diese zwischen Tor und Freistoßposition.

Berechnung

Bei all unseren Berechnungen bezüglich der Flugeigenschaften des Fußballes, gehen wir von dessen Unterkante aus.
Zuerst benötigen wir die allgemeine lineare Funktion f(x)=ax+b.
Wir definieren a als die Steigung des Schusses und b als Schnitt mit der Y-Achse.
Der erste Punkt liegt bei (0 / 2,24), da der optimale Eintreffpunkt bei 2.24m liegt.
Ein weiterer Punkt finden wir bei (16 / 0). Dies ist die für das Modell angenommene Freistoßmarke.

Zyklus 1 - perfekte Freistoßkurve als lineare Funktionen

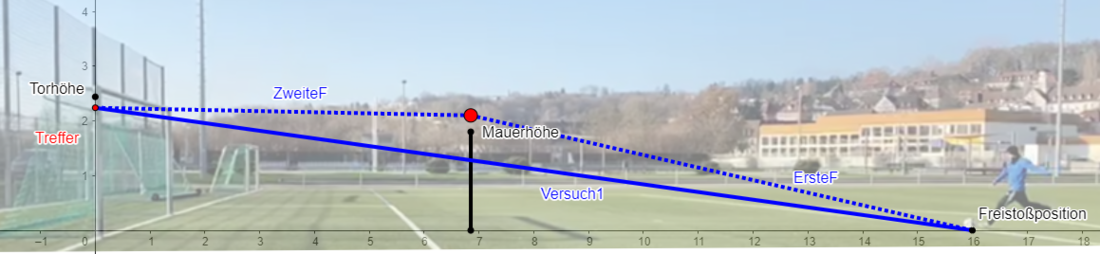
Nun muss ein Hindernis, hier in Form der Abwehrmauer, überwunden werden. Diese befindet sich zwischen Freistoßposition und Tor.
In unserem Schaubild ist der höchste Punkt der Mauer entweder bei Punkt (6,85/1,80) oder bei Punkt (6,85/2), je nachdem ob die „Mauer springt“ oder nicht.
Welcher der Werte berücksichtigt werden muss, hängt vom Zufall ab. Die zwei Werte werden jeweils zu 50% angenommen.
Die bereits ermittelte lineare Funktion F1 bildet einen Schnittpunkt mit der gegnerischen Mauer (Ausgangspunkt). Dieser muss so verändert werden, dass kein Schnittpunkt mehr vorliegt, da der Schuss sonst abgeblockt werden würde.
Daraus könne wir ableiten, dass sich die Werte a (Steigung) und b (Schnitt mit der Y-Achse) verändern.
Durch die Tabellenkalkulation in Excel [siehe Zyklus 1 - perfekte Höhe des Balles bei Mauerposition] kann der bestmögliche Punkt e, in diesem Fall (6,85/2,1), ermittelt und die Verbindung zur Freistoßposition als lineare Funktion und somit als Teil des optimalen Freistoßes festgesetzt werden.
Durch Verändern der Schusstechnik sowie Verlangsamen des Schusses, fällt der Ball ab einem gewissen Punkt ab. Diesen Vorgang haben wir vereinfacht ab dem Punkt e mit einer zweiten linearen Funktion F2 dargestellt. Dies ist die Strecke von e zu d.

Zyklus 2: (Niveau Sekundarsufe 2)

Rückblickend haben wir uns im ersten Zyklus mit einem Vollspannschuss und der damit einhergehenden linearen Funktion f(x)=ax+b beschäftigt.
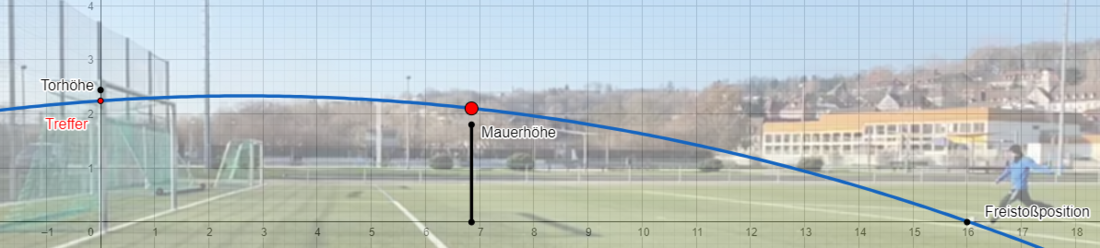
Nun geht es in unserem zweiten Zyklus weiterführend um den Schuss mit der Innenseite des Fußes. Diese Art des Schusses ist notwendig, damit die Flugkurve des Balles in einem Bogen erfolgt.
Um diese mathematisch darstellen zu können, benötigen wir die allgemeine quadratische Gleichung f(x)=ax²+bx+c.
Wir haben unsere quadratische Gleichung anhand drei bereits gegebener Punkte berechnet:
Die Freistoßmarke bestimmt unseren ersten Punkt (16/0). Die Höhe des Balles bei der Mauer, hier (6,85/2,1), legt den zweiten Punkt und der Treffer ins Tor bei (0/2,24) den dritten Punkt fest.
Um die quadratische Funktion unseres „perfekten Freistoßes“ zu berechnen, nutzen wir das Programm wxMaxima.
Mit der nun berechneten Funktion f(x)=-0,013x²+0,069x+2,24 und den konkreten Höhen des Balles über der Mauer (x= 6,85) und im Tor (x=0), können wir dem Freistoßschützen verschiedene Handlungsempfehlungen liefern.
Diese Korrekturvorschläge können dem Schützen helfen, sich immer mehr an „die perfekte Freistoßkurve“ anzunähern.
Ähnlich des ersten Zyklus stellen wir diese Korrekturvorschläge als maschinelles Lernen in einer Tabellenkalkulation in Excel dar.

Zyklus 2 - perfekte Freistoßkurve als quadratische Gleichung

Berechnung

Vorgehen zur Berechnung der Gleichungssysteme in Maxima:

A⋅x=b ⇔ A^-1⋅A⋅x=A^-1⋅b ⇔ x=A^-1⋅b

Wir schreiben:

A≔pF; x≔(a,b,c)^T;b≔x_n

Konkret heißt dies für die perfekte Freistoßkurve:

pF =[(0, 16², 6.85²)^T; (0, 16, 6.85)^T; (1, 1, 1)^T];

x = (a, b, c);

x_n bzw. x₁=(2.24, 0, 2.1)^T

Es folgt die Berechnung der perfekten Freistoßkurve in wxMaxima mit den Wertepaaren:
(0/2,24) also die Position des Balles bei dem Einschlag in das Tor,
(6,85/2,1) die Ballposition an der Mauer und
(16/0) ist die Position des Balles an der Freistoßmarke.
Die Berechnung der weiteren Schusskurven ist analog dazu.

1.Schritt

1.Schritt

Wir definieren unsere Werte der perfekten Freistoßkurve als Matrix pF.
Diese besteht aus unseren x-Werten (siehe oben)
Anschließend wird ihre Inverse berechnet.

2.Schritt

2.Schritt

Wir geben nun unseren Lösungsvektor x₁ der perfekten Freistoßkurve (pF) ein.
Von wxMaxima lassen wir uns nun die Matrixmultiplikation pF⋅x₁ ausspielen.
Somit ergibt sich die Funktion unserer perfekten Freistoßkurve.

3.Schritt

3.Schritt

Mit dem Integral berechnen wir nun die Flächen zwischen unserer perfekten Freistoßkurve (-0.013x²+0.069x+2.24) und den Schüssen des Schützen.
Hier betrachten wir seinen ersten Schussversuch (-0.0125x²+0.0127x+3).
Dieses Verfahren führen wir nach gegebenen Handlungsempfehlungen für alle weiteren Schussversuche analog weiter.

4.Schritt

Mithilfe des Programmes wxMaxima konnten wir den Wert 5,64 für das Integral des ersten Schusses ermitteln.
Dadurch können wir dem Schützen nun Handlungempfehlungen und Verbesserungsvorschläge geben, sodas er seinen nächsten Schuss dementsprechend anpassen kann.
Anschließend wird wieder die Schussbahn des Balles ermittelt, in wxMaxima berechnet und eine weitere Korrekturempfehlung ausgesprochen.
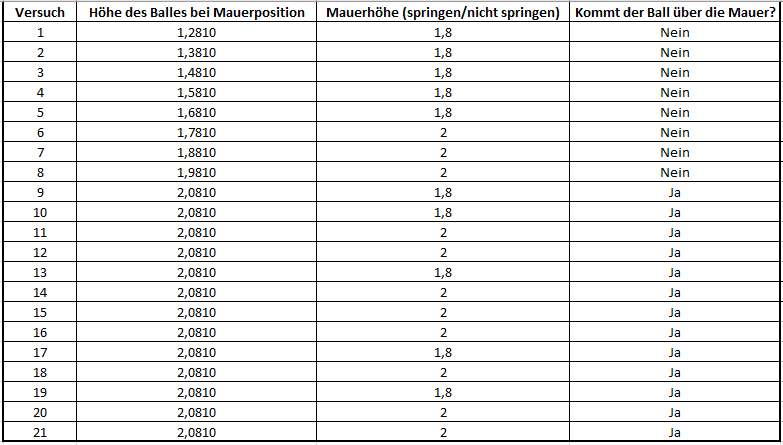
In der folgenden Tabelle wurden unsere Berechnungen festgehalten.
So wird schnell ersichtlich, dass die Schussversuche des Schützen aufgrund unserer errechneten Handlungsvorschläge immer besser werden.
Dies wird in der Tabelle (Zyklus 2- Handlungsempfehlungen) deutlich, da die Flächen zwischen den Funktionen (perfekte Freistoßkurve – Versuch n) immer geringer werden.
Kleinere Abweichungen sind natürlich nicht auszuschließen.

Zyklus 2 - Handlungsempfehlungen

Zyklus 3: (Niveau Universität)

In unserem dritten Zyklus schauen wir uns nun alle Torschussversuche des Schützen an. Besonders wollen wir uns auf die Anzahl der optimalen Treffer ins Tor fokussieren.
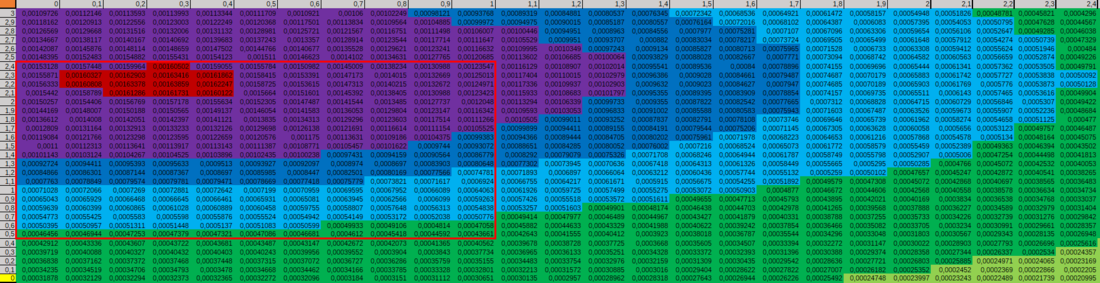
Um auswerten zu können, ob der Schütze mit unseren Handlungsempfehlungen eine Art Lernprozess entwickeln konnte, schauen wir uns das Koordinatensystem (siehe unten) an.
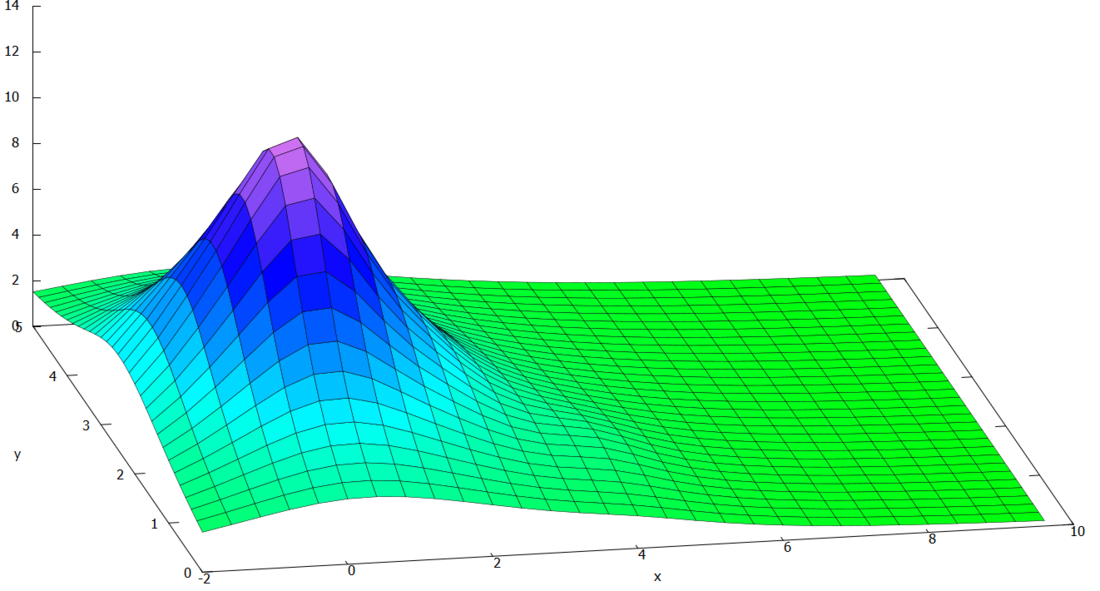
Dieses Schaubild zeigt die unterschiedlichen Wahrscheinlichkeitswerte des Schützen, den Ball mit der perfekten Freistoßkurve ins Tor zu treffen.
Mit der Wahrscheinlichkeitsdichte können wir klar erkennen, wie und wo sich die verschiedenen Merkmalsausprägungen verteilen und in welchem Bereich die meisten Schüsse einschlagen. Der Schütze hat 20 Freistöße ausgeübt.
In unserem Schaubild wird schnell deutlich, dass der Schütze mit den von uns vorgeschlagenen Korrekturmaßnahmen eher in der Lage ist, sich unserem "perfekten Freistoßtreffer" anzunähern. Diese Feststellung lässt sich durch den "höchsten Berg" im Diagramm belegen.
Ebenso kann man ein paar Fehlschüsse erkennen. Diese werden in der Grafik deutlich kleinere Hügel dargestellt und sind daher von geringerer Relevanz, da sie im Verhältnis zu den "erfolgreichen Schüssen" praktisch unerheblich sind. So sieht man beispielsweise ein paar Schüsse, die eher mittig einschlugen oder zu hoch. Folgende Schüsse konnten bei diesem Schützen gemessen werden (sie werden anschließend noch graphisch dargestellt):

f(x,y,x0,y0,h):=h/(1+Laenge(x-x0,y-y0)^2), mit Laenge(x,y):=sqrt(x^2+y^2)

Dichte(x,y):=f(x,y,0.2,2.24,1); f(x,y,0.2,3,1); f(x,y,2,2.6,1); f(x,y,0,2.3,1); f(x,y,-1,2.2,1); f(x,y,-0.5,2.2,1); f(x,y,0,2,1); f(x,y,0,2.3,1); f(x,y,0.2,2.2,1); f(x,y,0.3,2.2,1); f(x,y,0.5,2.5,1); f(x,y,0.5,2,1); f(x,y,0.3,2.2,1); f(x,y,1,2.3,1); f(x,y,0.8,2.5,1); f(x,y,0.4,2.3,1); f(x,y,0.3,2.2,1); f(x,y,0.3,2.1,1); f(x,y,2,1.8,1); f(x,y,0.2,2.1,1)

Trefferhäufigkeit bei 20 Schuss

Dichtefunktion Schussprofil F.M.

Abschließend kann man sagen, dass unsere Handlungsempfehlungen und Korrekturvorschläge dem Schützen weitergeholfen haben, seinen Schuss zum "perfekten Freistoßschuss" anzupassen.

Berechnung

Zunächst haben wir versucht das Doppelintegral: 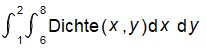zu berechnen. Jedoch kam wxMaxima an seine Grenzen. Es rechnete zu lange oder konnte nur nach einer Variabel (x oder y) aufleiten. Daher entschieden wir uns, numerisch bzw. annäherungsweise das Volumen zu berechnen.

Anhand einer Tabellenkalkulationssoftware (Excel) haben wir jeden Schuss einzeln in einem Intervall von x=[-1;6] und y=[0;3] dargestellt. Mit einer Schrittweite von 0,1 haben wir an jedem Punkt in dem Intervall die Höhe der Funktion berechnet. Diese haben wir am Ende summiert. Diesen Vorgang haben wir für die anderen Schüsse wiederholt. Dann konnten wir ein Schussprofil des Schützen erstellen, indem wir die jeweiligen Werte an allen Punkten summiert haben.

Nun wollten wir wissen, wie genau der Schütze bzw. seine 20 Schüsse waren. Dazu haben wir berechnet, wie wahrscheinlich es ist, dass der Schütze in einem vorgegebenen Intervall (um den perfekten Freistoß rum) trifft.

Es zeigt sich, dass rund 23 Prozent der 20 Schüsse im Bereich x=[0.0;1.0] und y=[0.5;2,4] liegen. Die Grundmenge bzw. der komplette Bereich war bis zu maximal den Außreißern bestimmt. Das heißt wir haben uns nur den Bereich angeschaut, in dem gerade so alle 20 Schüsse vorkamen.

Volumenberechnung

Fazit

Insgesamt zeigen die Modellierungen, dass der Freistoßschütze sich anhand unsere Handlungsempfehlungen verbesserte. Nicht nur hat er einen Richtwert für die Höhe des Balles über die Mauer (Zyklus1) erhalten, sondern auch die Erkenntnis gewonnen, dass ein Spannschuss unter der Berücksichtigung der Bedingungen nicht sinnvoll ist. Jedoch muss kritisch hervorgehoben werden, dass einige Einflussfaktoren (externe Faktoren), wie etwa Wetter, Material und Platzbedingungen, sowie (interne Faktoren) Begabung, etc. nicht berücksichtigt werden.

Trotz dieser kritisch hervorgehobenen Punkte muss man die Anwendung in der Schule hervorheben. Eine Anwendung ist möglich. Ein Schussprofil für jeden Schützen kann angefertigt werden. Sowohl Zyklus 1 und Zyklus 2 betrachten Funktionen bzw. Parameter von Funktionen und können daher im Schulunterricht Anwendung finden. Zyklus 3 hingegen scheint auf dem ersten Weg schwierig, dennoch kann dieser aufgrund einer numerischen Vorgehensweise durch eine Tabellenkalkulation vereinfacht dargestellt werden.

Zudem ist zu erwähnen, dass unter anderem auch wxMaxima seine Grenzen hat (Zyklus 3) und man dadurch gezwungen ist andere Programme mit aufwendigen Schritten zu verwenden.

Wiki2Reveal

• Einführung [2]
• Zyklus 1 [3]
• Zyklus 2 [4]
• Zyklus 3 [5]
• Bewertung der Modellbildung [6]
• komplette Präsentation [7]