Kurs:Mathematische Modellbildung/Themen/Perfekter Freistoß/Zyklus 2
Erscheinungsbild
Vorgehen
[Bearbeiten]- Erkenntnisgewinn aus Zyklus 1: Schusstechnik wird entsprechend angepasst
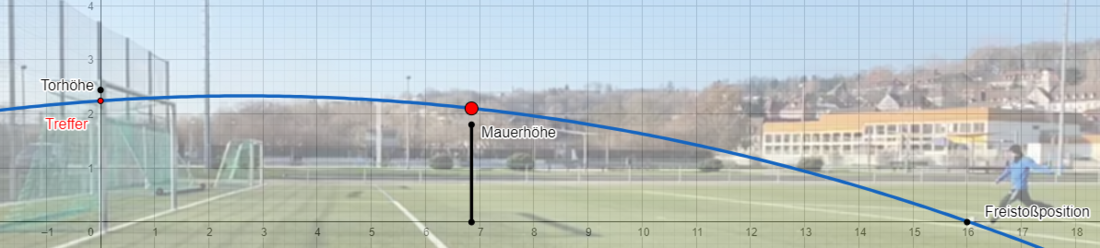
- Betrachten der perfekte Freistoßkurve nun als quadratische Funktion
- Berücksichtigen des Punktes (6,85/2,10)
- Verbesserung der Schusstechnik durch Differenz der Integrale sichtbar
Perfekte Flugkurve
[Bearbeiten]- Ziel: Durch Handlungsempfehlungen der "perfekten" quadratischen Funktion annähern
Herleitung Integral (1)
[Bearbeiten]- Idee: Einteilung der Fläche in viele kleine Rechtecke
- Rechtecke berechnen sich als Höhe x Breite, d.h. f(Stützwert) x Abstand der x-Werte
- Breite der Rechtecke ist äquidistant, d.h. gleich breit
- Fläche entspricht der Summe der unendlich vielen und kleinen Rechtecke
Herleitung Integral (2)
[Bearbeiten]- Abstand der x-Werte der Rechtecke geht gegen 0 und heißt Differential (dx)
- Riemann-Integral ist somit die unendliche Summe von den unendlich kleinen Rechtecken
Definition Integral
[Bearbeiten]
Berechnung
[Bearbeiten]wxMaxima
[Bearbeiten]- Berechnung der Freistoßfunktionen anhand eines Gleichungssystem der Form A*x=b
- b:= gemessene Werte, an den Stellen (x=0, x=16, x=6,85)^T
- Gleichungssystem auflösen nach x:= (a,b,c) durch Multiplikation mit A^-1 auf beiden Seiten
- Dann kann die Funktionsgleichung der Form f(x)= ax² + bx + c abgelesen werden
Exemplarische Berechnung
[Bearbeiten]
- --> Perfekte Freistoßkurve: f(x)=-0,013x²+0,069x+2,24
Geogebra
[Bearbeiten]- Berechnung der Fläche zwischen den realen Schüssen und der perfekten Kurve
Tabellenkalkulation (1)
[Bearbeiten]- Betrachtung der relevanten Punkte: Tor (2,24) und Mauer (2,1)
- Wenn der Schuss z.B. deutlich über die Mauer geht soll der Schütze nächstes mal tiefer gehen
- Wenn der Schuss in die Mauer geht, dann soll der Schütze nächstes mal höher schießen
- Analog erfolgt eine Handlungsempfehlung mit Blick auf die Höhe des Balles im Tor
Tabellenkalkulation (2)
[Bearbeiten]- Berechnete Flächen aus Geogebra dienen zur Interpretation

Ergebnisse
[Bearbeiten]- Durch individuelle Handlungsempfehlungen konnten wir die Schusstechnik des Schützens verbessern bzw. der perfekten Kurve annähren
- Handlungsempfehlungen dienen jedoch nur als grobe Orientierung
- Genauere Analyse des Schussprofils nötig (Zyklus 3)

