Kurs:Mathematische Modellbildung/Themen/Perfekter Freistoß/Zyklus 3

Vorgehen

Zunächst haben wir das Schussprofil (20 Freistöße) mittels einer Dichtefunktion erfasst. Anhand dieser konnten wir das Schussprofil graphisch darstellen und interpretieren.

Dichtefunktion allgemein

Eine Funktion f heißt Dichtefunktion (oder Dichte), falls folgende Bedingungen gelten:

f(x) ≥ 0 für alle x aus der Ergebnismenge
f ist integrierbar

Ihre Höhe gibt keine Wahrscheinlichkeit, sondern Dichte an.

Unsere Dichtefunktion

f(x,y,x0,y0,h):=h/(1+Laenge(x-x0,y-y0)^2)

Laenge(x,y):=sqrt(x^2+y^2)
x0 und y0 sind die gemessenen Einschlagskoordinaten eines Freistoßes
h ist die Häufigkeit
x und y sind die Koordinaten, die betrachtet werden

Wahrscheinlichkeitsdichtefunktion (WDF)

Bei uns bietet sich eine WDF an, da zwei Menschen nicht exakt gleich gut schießen bzw. zwei Schüsse kaum exakt gleich sind.

Mit so einer Funktion lässt sich nun die Wahrscheinlichkeit für ein beliebiges Intervall bspw. einer Schussgenauigkeit in einem bestimmten Bereich bestimmen.

Definition WDF

f: R --> R heißt WDF, falls gilt:

f ist nicht negativ, d.h. f(x) ≥ 0 für alle x
f ist integrierbar
f ist normiert, in dem Sinne, dass
WDF Normiert.svg

dann ist f eine WDF und wie folgt definiert:

WDF

Diese Formel gilt genauso für die Intervalle (a,b), (a,b] und [a,b]. Denn die WDF gibt im stetigen Fall keine Wahrscheinlichkeit für einen konkreten Wert an. Die Wahrscheinlichkeit für einen konkreten Wert X ist P(X)=0.

Kennzahlen WDF

Erwartungswert:

Varianz:

Standardabweichung: Wurzel(Var(x))

Berechnung

wxMaxima

Folgendes Schussprofil (20 Schüsse) konnten wir mithilfe unserer Dichtefunktion erstellen:

Dichte(x,y):=f(x,y,0.2,2.24,1)+f(x,y,0.2,3,1)+f(x,y,2,2.6,1)+....

Problem?

Nun wollten wir mittels wxMaxima die Dichte in einem bestimmten Intervall berechnen und ins Verhältnis mit dem Gesamtintegral setzen. Leider kam wxMaxima bei diesem Doppelintegral an seine Grenzen. Jedoch konnten wir das Integral annäherungsweise mittels Tabellenkalkulation (Excel) berechnen.

Tabellenkalkulation

Bestimmung der Funktionswerte durch vorgegebene Schrittweite für x und y von 0,1.

Für jeden Schuss haben wir so einzelne Schussprofile (Tabellenblätter) angelegt.

Durch aufsummieren aller Schussprofile ergab sich ein Gesamtschussprofil (Dichte) der 20 Schüsse.

Dividiert man jede Zelle durch das Gesamtintegral (Summe Gesamtbereich) erhält man die WDF, da nun das Gesamtintegral bzw. Gesamtsumme 1 entspricht.

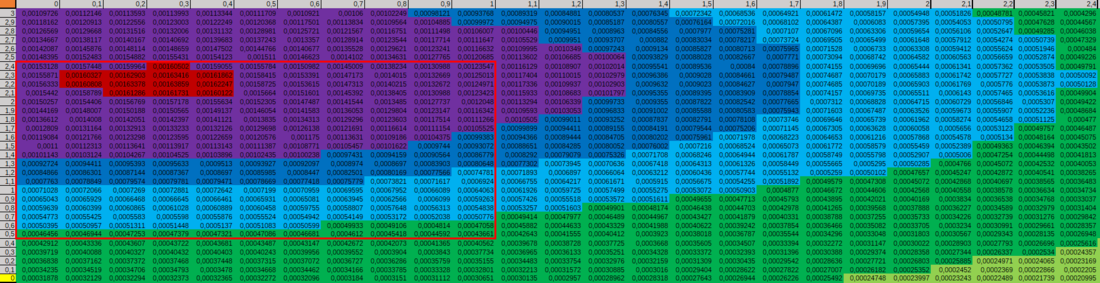
Darstellung - Geogebra

Ergebnisse

Maxima ist an seine Grenzen gekommen (Berechnungen der Integrale)
Daher näherungsweise Bestimmung des Volumens durch Excel
Im näherungsweise "interessanten Intervall": x=[0,1] und y=[0.5,2.4] liegen ca. 23%
Einschränkend muss erwähnt werden, dass wir als Gesamtintervall nur x ∈ [-1,6] und y ∈ [0,3] betrachtet haben, da -inf bis inf via Excel nicht darstellbar ist