Kurs:Mathematische Modellbildung/Themen/Volumenschätzung und Verbrauch von Ressourcen/Mathematische Lernvoraussetzungen Uni
Erscheinungsbild
Mathematische Lernvoraussetzungen - Niveau Uni
[Bearbeiten]Funktionen
[Bearbeiten]- Zuordnung zwischen einer Definitionsmenge und einer (Ziel-) Menge , die jedem Element x aus genau ein Element y aus zuordnet:
Wellenfunktion
[Bearbeiten]- beschreibt die Auslenkung eines von der Welle erfassten Teilchens in y-Richtung an einem beliebigen Ort x zu einem beliebigen Zeitpunkt t
- beschreibbar mithilfe der Sinus- oder Kosinus-Funktion
- 2π-periodische Wellenfunktion:
- abflachender/dämpfender Faktor:
- abflachender Faktor wird bei späterer Funktion weggelassen, da Faktor sehr groß wird und dadurch der Nenner des abflachenden Faktors sehr langsam abnimmt
- Betrachtung des Integrals am Ursprung der Funktion
Abschätzen von Funktionen
[Bearbeiten]- Abschätzungen von Funktionen mithilfe oberer Grenzen und Näherungsfaktoren
- unbestimmtes Integral
- F ist eine Funktion, deren erste Ableitung die ursprüngliche Funktion f ist
- F heißt Stammfunktion von f
- bei Addition und Subraktion einer beliebigen Zahl zu F, erhält man eine weitere Stammfunktion
- bestimmtes Integral ergibt eine Zahl: entspricht der Fläche zwischen dem Funktionsgraphen und der x-Achse
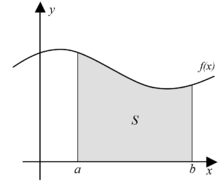
- Sei eine reelwertige stetige Funktion auf dem abgeschlossenen Intervall :
für alle ist die Integralfunktion mit differenzierbar und eine Stammfunktion von
für alle gilt:
- Sei eine stetige Funktion mit Stammfunktion
Berechnung Integral in den Integrationsgrenzen a und b:
.
Rotationsvolumen
[Bearbeiten]Rotation einer Sinuskurve
[Bearbeiten]
Rotation um die x-Achse
[Bearbeiten]- durch Drehung einer Kurve um die x-Achse ensteht ein Rotationskörper mit Volumen V
- Volumen berechnet sich im Intervall folgendermaßen:
Rotation um die y-Achse
[Bearbeiten]- durch Drehung einer Kurve um die y-Achse ensteht ein Rotationskörper mit Volumen V
- Volumen berechnet sich mithilfe der Umkehrfunktion mit stetig und monoton im Intervall folgendermaßen: mit und Grenzen des Wertebereichs mit oder:







![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
![{\displaystyle [a,b]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a659536067aaaac2db1c44613a09a715f0cf7246)
![{\displaystyle x_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06636653315ee7c3b5dc9bdb6ac3fb8cccadc145)
![{\displaystyle F\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/22aae183016ffbb759663208b693d6a28be4e69e)


![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)

![{\displaystyle \int _{a}^{b}f\left(x\right)dx=\left[F(x)\right]_{a}^{b}=F\left(b\right)-F\left(a\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e63f62d4c55d7fe69c3a69dfacb707cb72e0cef7)
![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)







