Kurs:Mathematische Modellbildung/Themen/Volumenschätzung und Verbrauch von Ressourcen
Vorwort
[Bearbeiten]In diesem Projekt wird für die Elefantendame Aruba des Kronberger Opel-Zoos ein Schwimmbecken konstruiert. Dabei wird der Beitrag zum Arterhalt, sowie eine Tierhaltung, die "stets hohen Anforderungen genügt" außer Betracht gelassen.
Modellierungsproblem
[Bearbeiten]Einleitung und Motivation
[Bearbeiten]An heißen Tagen brauchen Elefanten je nach Größe bis zu 150 Liter Wasser am Tag. Damit liegen sie nur knapp über dem durchschnittlichen Verbrauch der Menschen – in Hessen sind es 121 Liter Trinkwasser pro Kopf und Tag.
Die Elefantendame Aruba ist jedoch nicht die größte Wasserverbraucherin im Kronberger Opel-Zoo. Den höchsten Bedarf haben nach Auskunft des Zoodirektors die Flusspferde, weil ihre Becken einmal pro Woche gereinigt werden müssen. Mitarbeiter befüllen die beiden Becken mit Brauchwasser. Jedes fasst 20 Kubikmeter Flüssigkeit, das sind 20.000 Liter. Etwa die gleiche Menge pro Woche fließt über einen ständigen Zulauf in das Refugium der massigen Säugetiere.
Auch zum Reinigen der Gehege der übrigen Tiere verwenden die Zoomitarbeiter fast ausschließlich Brauchwasser. Es besteht aus Regenwasser, das der Tierpark in Zisternen sammelt und Wasser, das er aus zwei eigenen Brunnen gewinnt.
Pro Jahr benötigt der Zoo nach Angaben von Direktor Thomas Kauffels rund 26.000 Kubikmeter Wasser, drei Viertel davon sind Brauchwasser. Trinkwasser wird in der Verwaltung und im Besucherbereich verwendet. Um das Futter der Tiere zuzubereiten und die Futterküchen zu reinigen, benutzen die Tierpfleger ebenfalls Trinkwasser. [1]
Ziel der Modellierung
[Bearbeiten]Damit Aruba durch den Bau ihres Schwimmbeckens nicht zur größten Wasserverbraucherin des Zoos wird, sollen beim Bau und Befüllen des Beckens bestimmte Maßnahmen beachtet werden um den Wasserverbrauch möglichst gering zu halten.
Zunächst soll das Schwimmbecken nicht komplett mit Wasser befüllt werden, sondern durch eine geeignete Volumenschätzung von Aruba bestimmt werden, wie viel Wasser eingefüllt werden darf, sodass beim Baden von Aruba kaum Wasser verloren geht.
Da Aruba auch gerne mal etwas stürmiger ins Wasser geht und dabei eine Wasserwelle ensteht, soll eine große Glasscheibe dafür sorgen, dass die Welle an dieser abprallt und das Wasser wieder zurück in das Schwimmbecken fließen kann.
Schlussendlich wird Aruba "gedanklich" durch einen riesigen Eisblock ersetzt. Wenn dieser anfängt zu schmelzen, steigt der Wasserspiegel ähnlich wie bei einem Elefanten beim Baden. Ist das Schwimmbecken voll bevor der Eisblock vollständig geschmolzen ist, läuft das Wasser über den Beckenrand hinaus und überschwemmt angrenzende Umgebungen. Dieses Phänomen kann also vom Kleinen zum Großen übertragen werden. Während Aruba beim Baden in ihrem Schwimmbecken für eine minimale Überschwemmung ihrer Umgebung sorgt, sorgen riesige Eisblöcke in der Arktis, welche sich aufgrund der Erderwärmung lösen und beginnen zu schmelzen, für einen ansteigenden Meeresspiegel und Überflutungen auf der ganzen Welt. [2]
Zielgruppe der Modellbildung
[Bearbeiten]Die ersten beiden Zyklen der Modellierung entsprechen den Anforderungen der Sekundarstufe I und II, sodass auch die Schülerinnen und Schüler dieser Altersgruppe angesprochen werden sollen. Die SuS erfahren durch die sozialen Netzwerke häufig, dass in vielen Regionen der Welt, Wassermangel ein ernstes Problem ist - und auch wir in Deutschland teilweise dazu beitragen. So kann durch die Modellierung den SuS bewusst gemacht werden, dass jeder einzelne Mensch gegen das Aufrechterhalten wichtiger Ressourcen auf seine eigene Art und Weise was tun kann um den weltweiten Wassermangel zu stoppen.
Durch diese Modellbildung wollen wir den SuS mithilfe eines Zoos deutlich machen, wie man bei solch parkähnlich angelegten Geländen, die im Gegensatz zur Landwirtschaft viel, viel weniger Wasser benötigen, anfangen kann, Wasser zu "sparen" und effizienter zu nutzen um die Aufrechterhaltung wichtiger Ressourcen zu gewährleisten. Denn viele Schulen besuchen beispielsweise an Wandertagen Zoos und die SuS sind sich eigentlich gar nicht bewusst darüber, dass man schon durch das effiziente Befüllen des Schwimmbeckens von Aruba (siehe Modellierungszyklus 1) einiges an Wasser sparen und an anderer Stelle sinnvoll einsetzen kann.
Vor allem der letzte Modellierungszyklus soll Regierungen aller Länder auf das Eisschmelzen in der Arktis aufmerksam machen, denn die Region rund um die nördliche Polkappe erwärmt sich schneller als der Rest der Welt. Die steigenden Temperaturen in der Arktis bleiben nicht ohne Folgen: Das "ewige" Eis rund um den Nordpol schmilzt. Zwischen 2011 und 2020 war die jährliche durchschnittliche durch Eis bedeckte Fläche im arktischen Meer so gering wie seit mindestens 1850 nicht mehr. Und im Spätsommer - ein Zeitpunkt, zu dem das arktische Eis sein jährliches Minimum erreicht - war das von Eis bedeckte Gebiet so klein wie seit mindestens tausend Jahren nicht mehr. [3] Dieses Eis trägt zum Meeresspiegelanstieg bei, welcher sämtliche Küstenregionen der Erde - etwa durch Küstenerosionen, Sturmfluten und Überschwemmungen. Länder, die sich keinen Küstenschutz leisten können, sind am stärksten davon betroffen. [4]
Mehrwert der Modellbildung
[Bearbeiten]Wasser ist nicht nur das wichtigste Lebensmittel. Es wird auch im Haushalt, für Landwirtschaft, Industrie und in Zoos dringend benötigt. Der weltweite Wasserbedarf steigt, denn die Weltbevölkerung wächst – und ihre Konsumbedürfnisse nehmen zu. Das kann die Konkurrenz um das Wasser in manchen Regionen verschärfen. Gleichzeitig führt der Klimawandel zu Veränderungen im globalen Wasserhaushalt.
In Deutschland selbst ist Wassermangel normalerweise kein Problem, es ist ein wasserreiches Land. Doch extreme Dürre wie im Sommer 2018 wirft auch hier die Frage auf, wie sich die Verfügbarkeit von Wasser entwickelt, wenn es durch den Klimawandel häufiger zu Dürre- und Hitzeperioden kommt. Insgesamt ist die Versorgung in Deutschland sicher, doch in manchen Regionen sind unter Umständen Schwierigkeiten bei der Versorgung möglich. [5]
Allerdings löst der Begriff "Wasser" im ersten Moment sicher nur positive Gefühle aus, denn Wasser ist, wie bereits erwähnt, unersetzliche Grundlage für einen gesunden Naturhaushalt und wichtigstes Lebensmittel. Gleichzeitig kann Wasser aber auch unermessliches Leid ebenso wie Bedrohung, Furcht und Schrecken bedeuten, wenn wir an Dürre, Wassermangel, verseuchte Brunnen, Überschwemmungen und Muren denken. Wasser ist Leben und Wasser ist auch Tod. Seit jeher vereint das Element Wasser dieses konträre Potenzial in sich: Wasser, Fluch und Segen. [6]
Wiki2Reveal
[Bearbeiten]- Einführung (Foliensatz)

- Mathematische Lernvoraussetzungen Sek I (Foliensatz)

- Mathematische Lernvoraussetzungen Sek II (Foliensatz)

- Mathematische Lernvoraussetzungen Uni (Foliensatz)

- Modellierungszyklus 1 (Foliensatz)

- Modellierungszyklus 2 (Foliensatz)

- Modellierungszyklus 3 (Foliensatz)

Zuordnung zu den Nachhaltigkeitszielen
[Bearbeiten]
Beispiel für eine Textaufgabe im Mathematikunterricht
[Bearbeiten]Um die Modellierung im Schulalltag passend einzubetten, wäre ein Klassenausflug in einen Zoo empfehlenswert. Folgende Textaufgabe kann nach dem Zoobesuch in einer Unterrichtsstunde gemeinsam bearbeitet werden:
Der Kronberger Opel-Zoo möchte sein bereits vorhandenes Elefantengehege mit dem Bau eines Schwimmbeckens für Elefantendame Aruba erweitern. Das Schwimmbecken wird hierbei in Form eines dreieckigen Prismas mit folgenden Maßangaben gebaut: 12 m lang, 8 m breit und 6 m tief. Damit Aruba durch den Bau ihres Schwimmbeckens nicht zur größten Wasserverbraucherin des Zoos wird, sollen beim Bau und Befüllen des Beckens bestimmte Maßnahmen beachtet werden um den Wasserverbrauch möglichst gering zu halten.
a) (Modellierungszyklus 1 - Sekundarstufe I) Um möglichst wenig Wasser zu verbrauchen, wollen die Tierpfleger wissen, wieviel Wasser sie in das Becken einfüllen können. Da die Elefantenwaage zur Zeit aber noch nicht funktionstüchtig ist, müssen die Tierpfleger das Gewicht von Aruba näherungsweise bestimmen. Zerlege zunächst das vorgegebene Modell des Elefanten in geeignte geometrische Körper und berechne dann die Volumina der einzelnen Körper um das Gesamtvolumen des Elefantes zu erhalten. Berechne zum Schluss wie viel Wasser die Tierpfleger einfüllen dürfen, sodass kein Wasser beim Baden von Aruba über den Beckenrand verloren geht. Für schnelle SuS: Finde eine allgemeine Formel durch die das Gewicht verschieden großer Elefanten, mithilfe des Durchmessers ihres Fußabdruckes, bestimmt werden kann.
b) (Modellierungszyklus 2 - Sekundarstufe II) Nun soll das Schwimmbecken noch mit einer großen Glasscheibe zu den Besuchern abgetrennt werden, sodass die Zoogäste Aruba beim Baden beobachten können ohne nass zu werden. Wenn die Elefantendame Anlauf nimmt und sich in das Becken fallen lässt, stößt sie eine große Welle los. Wir möchten einen Weg finden, die Höhe der Welle bestimmen zu können, um dann abzuschätzen wie hoch die Glasscheibe auf der Seite der Besucher über den Wasserstand ragen muss. Dabei ist zu beachten, dass die Welle am Anfang des Schwimmbeckens am höchsten ist und sich bei Ausbreitung immer weiter abflacht. Folgende Funktion beschreibt den Querschnitt der Welle, welche beim Baden von Aruba entsteht: .
Bestimme nun mithilfe von Geogebra und der angegebenen Funktion die Höhe der Welle an der Glasscheibe und daraus resultierend die Höhe der Glasscheibe, welche 30 cm über der Höhe der ankommenden Welle liegen soll.
Modellierungszyklus 1 - Niveau Sekundarstufe I
[Bearbeiten]Ziel der Modellierung
[Bearbeiten]In dieser Modellierung wird das Gewicht eines Elefanten annäherungsweise bestimmt, sodass sich daraus resultierend die Wasserverdrängung eines Elefanten beim Baden ergibt.
Mathematische Lernvoraussetzungen
[Bearbeiten]Zur Berechnung des Gewichts werden folgende Lerninhalte vorausgesetzt:
- Auf- und Umstellen einer Formel
- Rechnen mit Größen
- Kenntnisse über geometrische Körper und deren Formeln zur Volumenberechnung
- Volumenbestimmung durch Zerlegen
- Umrechnungen von Maßeinheiten
- Dreisatz
Zur Approximation des Volumens eines Elefanten benötigen wir die folgenden Formeln der grundlegenden geometrischen Körper:
| Figur | Volumen | Schaubild |
|---|---|---|
| Ellipsoid | 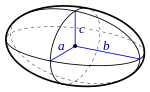
| |
| Zylinder | 
| |
| Kegel | 
|
Vorgehensweise
[Bearbeiten]Zunächst bestimmen wir das Gesamtgewicht eines Elefanten durch Zerlegung in einzelne Körperteile. Dazu nehmen wir verschiedene geometrische Körper und nähern diese den Körperteilen des Elefanten an, sodass wir im Anschluss die Volumina der einzelnen Körperteile berechnen können. Durch Addition der Volumina ergibt sich dann das gesuchte Gesamtvolumen des Elefanten.
Der Rumpf und der Kopf können jeweils durch einen Ellipsoid angenähert werden. Zur Darstellung der Beine, des Schwanzes und des unteren Teils des Rüssels kann jeweils die geometrische Form des Zylinders verwendet werden. Der obere Teil des Rüssels kann mit einem Kegel angenähert werden. Die Ohren werden hierbei aufgrund des geringen Gewichts, verglichen mit dem schweren Rumpf des Elefanten, vernachlässigt.
Davon ausgehend wird ein beispielhaftes Modell in JSON 3D Editor for AFrame erstellt. Mithilfe dieses Modells können die Parameter, wie Länge, Höhe und so weiter, der einzelnen geometrischen Körper bestimmt werden. Durch das Einsetzen der Größen in die Voluminaformeln der einzelnen Körperteile, erhalten wir durch Addieren der einzelnen Volumina schließlich das Gesamtvolumen eines Elefanten. Mit dem Gesamtvolumen des Elefanten können wir dann die Wasserverdrängung im Schwimmbecken bestimmen und wissen wie viel Wasser in das Schwimmbecken eingefüllt werden darf.
Durchführung
[Bearbeiten]Größenangaben eines Elefanten
[Bearbeiten]Die Größenangaben, welche benötigt werden um ein geeignetes Modell eines Elefanten zu erstellen, ergeben sich idealerweise aus dem Biologieunterricht der Sekundarstufe I oder können im Internet nachgeschaut werden. [7] Genauso kann ein Bild eines Elefanten zur Abschätzung der Größen genutzt werden. Durch einen nebenstehenden Tierpfleger können die Größenangaben des Elefanten noch besser abgeschätzt werden.
Modellierung eines Elefanten in JSON 3D Editor for AFrame
[Bearbeiten]Zu Beginn der Erstellung eines Elefanten in JSON 3D Editor for AFrame werden der Rumpf und der Kopf mithilfe zweier Ellipsoide annäherungsweise dargestellt. Dabei bildet der Mittelpunkt des Ellipsoids den Mittelpunkt des Rumpfes des Elefanten ab. Die Beine werden jeweils durch einen Zylinder angenähert, sodass jedes Bein des Elefanten gleichweit von dem Mittelpunkt des Rumpfes entfernt ist. Zusätzlich ist das vordere, linke Bein das Spiegelbild des vorderen, rechten Beins gespiegelt an der z-Achse. Gleiches gilt für die beiden hinteren Beine.

Folgende Werte werden aus der Modellierung des Elefanten in JSON 3D Editor for AFrame zur Berechnung der Volumina der einzelnen Körperteile entnommen und werden in Längeneinheiten (LE) angegeben:
Ellipsoid (Rumpf des Elefanten)
[Bearbeiten]Länge Rumpf:
Breite Rumpf:
Höhe Rumpf:
Ellipsoid (Kopf des Elefanten)
[Bearbeiten]Länge Kopf:
Breite Kopf:
Höhe Kopf:
Zylinder (Beine des Elefanten)
[Bearbeiten]Breite Bein:
Höhe Bein:
Volumen Bein:
Dreieck (Ohren des Elefanten)
[Bearbeiten]Die Ohren werden in JSON 3D Editor for AFrame jeweils als eine Fläche angenommen. Daraus folgt für das Volumen eines Ohres: .
Außerdem überschneiden sich stellenweise die Volumina der einzelnen geometrischen Körper im Modell, sodass sich die zwei fehlenden Flächen der Ohren dadurch ausgleichen lassen.
Zylinder und Kegel (Rüssel des Elefanten)
[Bearbeiten]Der Rüssel des Elefanten setzt sich aus zwei Rüsselteilen zusammen. Der untere Teil des Rüssels wird mithilfe eines Zylinders und der obere Teil des Rüssels mithilfe eines Kegels dargestellt.
Breite Rüssel (unten):
Höhe Rüssel (unten):
Breite Rüssel (oben):
Höhe Rüssel (oben):
Zylinder (Schwanz des Elefanten)
[Bearbeiten]Breite Schwanz:
Höhe Schwanz:
Gesamtvolumen des modellierten Elefanten
[Bearbeiten]Die Volumina aller Körperteile des Elefanten summieren sich zum Gesamtvolumen:
Problematik der erhaltenen Zahl
[Bearbeiten]16,86 beträgt das Volumen des modellierten Elefanten in LE3. Dieser Wert lässt sich mittels Dreisatz, in das Gewicht eines Elefanten mit einem vorgegebenen Fußdurchmesser in cm3 umwandeln:
geg.: Fußdurchmesser , Modellfußdurchmesser
Daraus resultierend lässt sich folgende Formel aufstellen:
Die aufgestellte Formel zur Berechnung des Volumens des Elefanten gilt allerdings nur für einen Fußdurchmesser von 30 cm. Der Durchmesser des Fußes des Elefanten lässt sich zwar variieren, aber aufgrund des linear funktionalen Zusammenhangs weicht das erhaltene Ergebnis von der ursprünglichen Funktion ab, sodass die Funktion nur bei einem Fußdurchmesser getroffen wird.
In Folge dessen erstellen wir eine allgemeine Formel zur Berechnung des Gewichts verschiedener Elefanten anhand deren Fußdurchmessers.
Anmerkung: Um das Volumen eines Elefanten aus dem Gewicht zu folgern wird außerdem noch seine Dichte benötigt. Wir haben diese zu Beginn der Modellierung mit 1 abgeschätzt, da ein Elefant unter der Wasseroberfläche schwimmen beziehungsweise tauchen kann. Somit nehmen wir also an, dass dessen Dichte nicht viel größer als 1 sein kann. Da ein Elefant aber auch nicht auf der Wasseroberfläche schwimmt und untertauchen kann, ist seine Dichte mit ziemlicher Sicherheit kaum kleiner als 1. Aus der Formel, dass sich das Gewicht, beziehungsweise die Masse, aus dem Produkt der Dichte und des Volumens ergibt, lässt sich aus unserer Annahme (Dichte von 1) folgern, dass die Masse in diesem Fall gleich dem Volumen abgeschätzt werden kann.
Bewertung und Optimierung
[Bearbeiten]Eine allgemeine Formel zur Berechnung des Gesamtvolumen eines Elefanten in Abhängigkeit des Fußdurchmessers wird wie folgt ermittelt:
Nebenrechnung für von abhängig:
Nebenrechnung in Abhängigkeit von :
(Gewicht in )
(Gewicht in )
Zur Überprüfung auf Richtigkeit der allgemein aufgestellten Formel, wurden in der ersten Spalte der Exceltabelle 51 Zufallszahlen zwischen 25 und 45 cm Fußdurchmesser durch folgenden Excelbefehl: generiert. Die Begrenzung des Zufallsbereichs ergibt sich dabei aus dem Fußdurchmesser eines kleinen Elefanten von rund 25 cm, sowie eines ausgewachsenen Elefanten von rund 45cm.
In der zweiten Spalte wurde die ermittelte Formel eingeben und für den Parameter jeweils die voherige Zelle eingesetzt. Außerdem wurde die ursprüngliche Formel mit der Division von 1.000.000 ergänzt um das Gewicht des Elefanten direkt in Tonnen angeben zu können (z.B.: ) .
Um die Entwicklung der errechneten Gesamtgewichte in Abhängigkeit der jeweiligen Fußdurchmessern graphisch darzustellen, wurde in Ecxel ein Diagramm erstellt. Zusätzlich ergeben sich durch das Drücken der "Löschtaste" in der erstellten Exceldatei immer wieder neue Zufallswerte, die alle auf dem exponentiellen Graphen liegen.
 |
Modellierungszyklus 2 - Niveau Sekundarstufe II
[Bearbeiten]Ziel der Modellierung
[Bearbeiten]In dieser Modellierung wird die Höhe der ankommenden Welle, welche ein Elefant beim Baden erzeugt, an der Glasscheibe bestimmt, sodass sich daraus resultierend die Höhe der Glasscheibe ergibt.
Mathematische Lernvoraussetzungen
[Bearbeiten]Funktionen
[Bearbeiten]- Zuordnung zwischen einer Definitionsmenge und einer (Ziel-) Menge , die jedem Element x aus genau ein Element y aus zuordnet:
Wellenfunktion
[Bearbeiten]- beschreibt die Auslenkung eines von der Welle erfassten Teilchens in y-Richtung an einem beliebigen Ort x zu einem beliebigen Zeitpunkt t
- beschreibbar mithilfe der Sinus- oder Kosinus-Funktion
- 2π-periodische Wellenfunktion:
- abflachender/dämpfender Faktor:
- Daraus folgt als annähernde Wellenfunktion:
Abschätzen von Funktionen
[Bearbeiten]- Abschätzungen von Funktionen mithilfe oberer Grenzen und Näherungsfaktoren
- unbestimmtes Integral:
- F ist eine Funktion, deren erste Ableitung die ursprüngliche Funktion f ist
- F heißt Stammfunktion von f
- bei Addition und Subraktion einer beliebigen Zahl zu F, erhält man eine weitere Stammfunktion
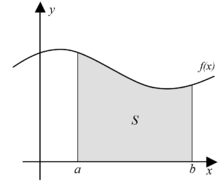
- bestimmtes Integral ergibt eine Zahl
- bestimmte Integral entspricht der Fläche zwischen dem Funktionsgraphen und der x-Achse
Sei eine reelwertige stetige Funktion auf dem abgeschlossenen Intervall , dann ist für alle die Integralfunktion
- mit
differenzierbar und eine Stammfunktion von , das heißt, für alle gilt .
Sei eine stetige Funktion mit Stammfunktion , dann gilt für die Berechnung des Integrals in den Integrationsgrenzen a und b:
Rotationsvolumen
[Bearbeiten]
Rotation um die x-Achse
[Bearbeiten]- durch Drehung einer Kurve um die x-Achse ensteht ein Rotationskörper mit Volumen V
- Volumen berechnet sich im Intervall folgendermaßen:
Rotation um die y-Achse
[Bearbeiten]- durch Drehung einer Kurve um die y-Achse ensteht ein Rotationskörper mit Volumen V
- Volumen berechnet sich mithilfe der Umkehrfunktion mit stetig und monoton im Intervall folgendermaßen:
- mit und Grenzen des Wertebereichs mit
- oder
Vorgehensweise
[Bearbeiten]Durch eine Funktion möchten wir eine Welle annähern. Sinus und Kosinus bieten sich dafür an und je nachdem wo die Welle beginnen soll, ist eine der Beiden sehr vorteilhaft.
Durch einen Faktor, den wir nennen, möchten wir diese Welle verzerrungsfrei skalieren, um den Wellenberg in der Mitte mit dem Gewicht des Elefanten abzuschätzen. Das Gewicht des zentralen Wellenbergs kann nicht übersteigen.
Durch einen weiteren Faktor lassen wir die Welle mit größerer Entfernung zum Ursprung abflachen.
Zur besseren Visualisierung erstellt man in Geogebra eine Datei. Das Programm bietet uns den Vorteil, einen Schieberegler für zu erstellen, mit dem wir durch Ausprobieren einen Wert finden können.
Hat man einen Parameter gefunden, welcher zum bereits bekannten korrespondiert, so kann man im Zusammenhang mit dem abflachenden Faktor in der Formel verwenden um einen Funktionswert für die Höhe der Welle bei gegebener Entfernung zur Wand zu berechnen.
Durchführung
[Bearbeiten]Die Elefantendame Aruba lässt sich mit vollem Einsatz in das Becken fallen und stößt eine große Welle los. Den Querschnitt der Welle lässt sich durch die Funktion beschreiben.

Betrachten wir nun die Funktion. Durch eine vollständige Rotation um die y-Achse wird die Welle dreidimensional. Das Volumen des größten Wellenbergs, in der Mitte, lässt sich nach oben abschätzen durch das Gewicht des Elefanten. Natürlich, denn es kann nach dem Eintauchen keine Welle entstehen, die eine größere Masse als der Elefant besitzt.
Zur Erinnerung, unsere Faustformel zur Berechnung des Gewichts anhand seines Fußdurchmessers lautet . Das Ergebnis wird in Kubikzentimetern angegeben und kann mit Division durch 1 000 000 in Kubikmeter, also metrische Tonnen, umgerechnet werden. Ab hier verwenden wir Meter als Angabe für beispielsweise die Höhe und Entfernung der Wand.
Betrachten wir den letzten Teil der Funktion , der gegeben wird durch . Da wir den übrigen Teil der Funktion mit einem bisher unbestimmten Skalierungsfaktor multiplizieren, können wir behaupten, dass eine obere Grenze für unsere Funktion darstellt. Diese werden wir verwenden um die Höhe der Welle zu bestimmen, jedoch benötigen wir dazu dringend den Faktor .

Der Faktor zur Skalierung der Größe der Welle lässt sich in einem dynamischen Geometriesystem, wie etwa GeoGebra, durch Ausprobieren annähern, doch er lässt sich durch ein paar Tricks auch rechnerisch bestimmen. Dazu benötigen wir das Integral von im Bereich bis , um dann mit dem Rotationsvolumen, die Masse des Wellenbergs zu bestimmen. Wir wählen hierbei den Maßstab: 1 Einheit im Koordinatensystem = 1 Meter. Aufgrund des Gewichts als oberer Grenze gilt .

Der Ausdruck beschreibt das Rotationsvolumen der Fläche . In GeoGebra können wir mit einem Schieberegler für die Masse des Wellenbergs annähern indem wir den Wert von variieren. Hierbei bietet es sich an eine Funktion mit aufzustellen. Durch Ausprobieren lässt sich ebenfalls ein ungefährer Bereich für festlegen. Für wird die zu gering für einen Babyelefanten, und für ist der Wellenberg schwerer als ein großer Elefant.
Leider gelangen wir so immer noch nicht rechnerisch an den Wert von , deshalb benötigen wir eine Hilfsfunktion, aus der wir ausklammern können. Wichtig dabei ist, dass die Funktion in der Nähe des Ursprungs nicht stark von der skalierten Funktion abweicht. Wir wählen die Funktion , und überprüfen diese bei verschiedenen Werten für auf Abweichungen.
Klar ist für , dass die Funktionen übereinstimmen und nicht von beeinflusst wird. liegt im Bereich und skaliert das Volumen des Wellenbergs, der von erzeugt wird, nicht jedoch, den von . Das Integral von im Bereich von bis ist nun ein fester Wert, gegeben mit . Für und im Bereich gilt: Die Amplitude von ist skaliert mit , und die obere Grenze des Integrals ist skaliert mit . Man kann bestimmen, dass das Integral beschreibt, wobei bekanntermaßen ein fester Wert bleibt.

Nun führen wir alle Schritte zusammen. Es gilt und . Daraus folgt dann . Rundet man , ergibt sich damit . Wir können also nun berechnen und die Funktion für die Höhe der Welle verwenden.
Sei der Abstand der Wand zum Eintrittsort des Elefanten. Diese Angabe lässt sich nicht allgemein bestimmen, da das Becken unterschiedliche Formen haben kann. So folgt letztlich für die Höhe der Wand an der Stelle : .
Beispiel - Durchführung
[Bearbeiten]Ein Elefant mit dem Fußdurchmesser besitzt das angenäherte Gewicht Tonnen. Der Skalierungsfaktor ist somit . Eine Wand, die 10 Meter entfernt von der Eintrittstelle entfernt ist muss also Meter hoch sein, damit die Welle nicht überläuft.
Bewertung und Optimierung
[Bearbeiten]Die obere Abschätzung der Welle zeigt die Höhe des Wassers, wo die Welle auf die Glasscheibe des Schwimmbeckens trifft. Somit können wir also mithilfe des Fußdurchmessers, insbesondere des Gesamtgewichts, eines Elefanten und der Entfernung zur Glasscheibe, die Höhe der ankommenden Welle an der Glasscheibe angeben. Daraus resultierend lässt sich dann die Höhe der Glasscheibe optimal bestimmen.
Das Auftreffen der Welle an der Glasscheibe, sowie deren Abprallen und Zurückwerfen in die entgegengesetzte Richtung, wird hier im Modell nicht betrachtet. Unbeachtet lassen wir auch die Tatsache, dass jedes Bein des Elefanten, eine eigene Welle erzeugen und diese sich jeweils kreisförmig ausbreiten kann. In unserem Modell springt der Elefant also vollständig in das Becken hinein.
Genauso wird die Form der Wellen hier mit der Kosinus-Funktion angenähert. Wie eine Welle im realen Leben aussieht, muss empirisch erprobt und beobachtet werden.
Für unsere aufgestellte Funktion der Welle, haben wir ein GeoGebra Applet erstellt. Mithilfe des dort erstellten Schiebereglers lässt sich der Fußdurchmesser eines Elefanten variieren. Hierbei gilt: je größer der Fußdurchmesser des Elefanten, umso höher auch das Gewicht. So vergrößert sich in unserem Applet mit Zunahme des Fußdurchmesser auch das Volumen der Welle. Ein weiterer Schieberegler gibt die Entfernung des Beckenrandes zur Glasscheibe an und ist ebenfalls beliebig veränderbar.
Im Folgenden erweitern wir unser Modell auf ein gesellschaftlich klimatisch wichtiges Thema. Wir wollen den Elefant auf ein ins Meer fallenden Eisblock übertragen und dessen erzeugte Welle auf mögliche Auswirkungen nahe gelegener Landmassen überprüfen.
Modellierungszyklus 3 - Niveau Uni
[Bearbeiten]Ziel der Modellierung
[Bearbeiten]
Wir übertragen unser Modell nun auf klimatisch gesellschaftlich wichtige Themen.
In dieser Modellierung wird die Höhe der ankommenden Welle, welche ein Eisblock bei der Kalbung eines Gletschers erzeugt, auf angrenzende Küstenregionen bestimmt, sodass sich daraus resultierend beispielsweise die Höhe eines Deiches oder sonstiger Schutzmaßnahmen ergibt.
Exkurs - Perito-Moreno-Gletscher
[Bearbeiten]
Der Perito-Moreno-Gletscher liegt im Los Glaciares Nationalpark und ist zugleich eine der größten Natur-Sehenswürdigkeiten im südlichen Patagonien. Jenseits der Pole bildet er den größten Gletscher im Inland und ist schon deshalb ein Ereignis der Superlative.
Seine fast haushohen Gletscherbrocken brechen mit einem schussähnlichen, sehr lauten Knacken ins Wasser und erzeugen dadurch riesige Wellen. Diesen tosenden Vorgang nennt man „Kalben“, denn hier schmilzt der Gletscher nicht, sondern bricht in Blöcken weg. Besucher müssen nicht lange auf dieses Spektakel warten, denn die fast 70 Meter hohe Gletscherfront des Perito-Moreno wirft kleinere Eisblöcke mehrfach im Stundentakt ab. Größeres Kalben, wenn der Gletscher bis an die Magellan-Halbinsel vorstößt und den Lago Argentino aufstaut und dann „zerdrückt“ wird, kommt in größeren, etwa halbjährlichen Abständen vor. [8]
Mathematische Lernvoraussetzungen
[Bearbeiten]Die mathematischen Lernvoraussetzungen sind analog zu Modellierungszyklus 2. Der Unterschied besteht lediglich in der Änderung der Wellenfunktion, welche auf die größeren Dimensionen des Gewichtes der abfallenden Gletscherteile angepasst wird.
Funktionen
[Bearbeiten]- Zuordnung zwischen einer Definitionsmenge und einer (Ziel-) Menge , die jedem Element x aus genau ein Element y aus zuordnet:
Wellenfunktion
[Bearbeiten]- beschreibt die Auslenkung eines von der Welle erfassten Teilchens in y-Richtung an einem beliebigen Ort x zu einem beliebigen Zeitpunkt t
- beschreibbar mithilfe der Sinus- oder Kosinus-Funktion
- 2π-periodische Wellenfunktion:
- abflachender/dämpfender Faktor:
Der abflachende Faktor wird bei der späteren Funktion ausgelassen, da wir davon ausgehen, dass der Faktor sehr groß wird und dieser im Nenner des abflachenden Faktors nur sehr langsam abnimmt. Je näher man am Ursprung ist, desto weniger hat dieser Faktor eine Auswirkung auf die Funktion und kann deswegen auch weggelassen werden, da wir nur das Integral am Ursprung betrachten.
Abschätzen von Funktionen
[Bearbeiten]- Abschätzungen von Funktionen mithilfe oberer Grenzen und Näherungsfaktoren

- unbestimmtes Integral:
- F ist eine Funktion, deren erste Ableitung die ursprüngliche Funktion f ist
- F heißt Stammfunktion von f
- bei Addition und Subraktion einer beliebigen Zahl zu F, erhält man eine weitere Stammfunktion
- bestimmtes Integral ergibt eine Zahl
- bestimmte Integral entspricht der Fläche zwischen dem Funktionsgraphen und der x-Achse
Sei eine reelwertige stetige Funktion auf dem abgeschlossenen Intervall , dann ist für alle die Integralfunktion
- mit
differenzierbar und eine Stammfunktion von , das heißt, für alle gilt .
Sei eine stetige Funktion mit Stammfunktion , dann gilt für die Berechnung des Integrals in den Integrationsgrenzen a und b:
Rotationsvolumen
[Bearbeiten]
Rotation um die x-Achse
[Bearbeiten]- durch Drehung einer Kurve um die x-Achse ensteht ein Rotationskörper mit Volumen V
- Volumen berechnet sich im Intervall folgendermaßen:
Rotation um die y-Achse
[Bearbeiten]- durch Drehung einer Kurve um die y-Achse ensteht ein Rotationskörper mit Volumen V
- Volumen berechnet sich mithilfe der Umkehrfunktion mit stetig und monoton im Intervall folgendermaßen:
- mit und Grenzen des Wertebereichs mit
- oder
Vorgehensweise
[Bearbeiten]Die Welle, welche durch die Kalbung eines Gletschers entsteht, nähern wir mithilfe der Kosinus Funktion an. Im Vergleich zur Sinus Funktion bietet die Kosinus Funktion den Vorteil, dass diese an der y-Achse bei dem Funktionswert 1 einen ihrer Hochpunkte hat.
Wie bereits in Zyklus 2 greifen wir auf den Skalierungsfaktor zurück, um die Welle verzerrungsfrei darzustellen und den zentralen Wellenberg mit dem Gewicht des Gletscherbrockens maximal abzuschätzen.
Wir nehmen an, dass die Form des Gletscherbrockens keine Rolle spielt sondern nur allein das Gewicht des Brockens. Dadurch beschreiben wir das Volumen des Brockens mithilfe eines symmetrischen Zylinders.
Die Volumina des Zylinders und dem zentralen ersten Wellenberg sind hierbei identisch. Dadurch kann man annehmen, dass im Zweidimensionalen die Flächen der Kosinus Funktion und dem Rechteck, aus welchem durch Rotation der symmetrische Zylinder entsteht, ebenfalls identisch sind.
Hieraus können die Seitenlängen des Rechtecks und mithilfe des Skalierungsfaktors und des Gewichts abgeschätzt werden.
Die obere Abschätzung der Wellenfunktion erhält man durch die -Funktion.
Durchführung
[Bearbeiten]Beim Ausdehnen des Modells auf sehr große Maßstäbe, wie beispielsweise bei einem hundert Millionen Tonnen schweren Eisbrocken, welcher aufgrund der Gletscherkalbung ins Wasser fällt, ist es nicht von Bedeutung, welche Form dieser besitzt. Allein die Masse genügt um ein sinnvolles Modell zu erstellen. Aus diesem Grund lässt sich das Volumen aus Symmetriegründen vorteilhaft mithilfe eines Zylinders beschreiben.
Die entstehende Welle, nach dem Aufprall, lässt sich wieder durch das Gewicht als obere Grenze abschätzen, indem wir das Rotationsvolumen der Funktion im Bereich von bis berechnen. Somit ist mit . Um hierbei von dem Gewicht eines Eisblocks auf das Volumen schließen zu können, müssen wir das Gewicht mit der Dichte von Eis multiplizieren.

Für ein Rechteck der selben Fläche, also gilt folglich . Wenn ein in Abhängigkeit von existiert für das gilt, so wählen wir die Position des Rechtecks so, dass durch Rotation von ein Zylinder entsteht.

Zur besseren Veranschaulichung haben wir ein GeoGebra Applet erstellt.
Wie in der Abbildung dargestellt, sind die Kantenlängen des Rechtecks gerade und und somit gilt .
Es folgt:
Dabei ist die Annahme zu beachten, dass stets positiv sein muss, weshalb keine Fallunterscheidung von Beträgen beim Wurzelziehen nötig ist.
Nun, da man mit gegebenem (oder geschätztem) Gewicht ein korrelierendes herausgefunden werden kann, muss noch ein passendes gefunden werden. Die Funktion kann so angepasst werden, dass es leichter fällt Faktor a herauszufinden, ohne jedoch die Fläche A zu verändern.
Es gilt:

Bei Betrachtung der Funktion fällt auf, dass eine Hilfsfunktion aufgestellt werden kann, mit , für die das Integral ist. ist von doppelter Amplitude, aber von halber Länge und das Maß der Fläche ist gleich.

Analog zu Zyklus 2 gilt nun . Die Beziehung der Flächen zueinander ist in folgendem GeoGebra Applet dargestellt.

Es folgt:
Da man jetzt ein bestimmen kann, können wir dieses verwenden um die Höhe der Welle zu bestimmen indem wir es in einsetzen, wobei mit die Entfernung vom Zentrum bis zum nächsten Festland beschrieben wird. Beachte, dass hier die x-Achse in Kilometern gemessen wird.
Beispiel - Durchführung
[Bearbeiten]Gegeben sei ein großer Eisbrocken der Masse .
einsetzen in
Daraus folgt, dass bei einer Küste, welche entfernt ist, die losgestoßene Welle 3,46 m hoch ist.
Bewertung und Optimierung
[Bearbeiten]In dieser Modellierung betrachten wir die Gletscherkalbung. Dabei lassen wir das Schmelzen schwimmender Eisberge, welche zur Erhöhung des Meeresspiegels beitragen, sowie der Anstieg der Wassertemperatur, welche ebenfalls für die Kalbung der Gletscher verantwortlich ist, außer Betracht.
Zusätzlich ist anzumerken, dass es sich hierbei um eine Idee handelt und die Übertragung des ursprünglichen Modells aus Zyklus 2 auf große Maßstäbe nicht fehlerfrei geschehen kann. Würde man dieses Modell präzisieren wollen, müsste man Forschungen betreiben, wie weit sich Wellen ausbreiten bis sie letztendlich abflachen und einen Weg finden die Frequenz der Wellen gezielt darzustellen.
Eine weitere Möglichkeit dieses Modell zu verbessern, könnte sein, hinsichtlich der Globalen Erderwärmung und deren Auswirkungen auf Küstenregionen, eine interaktive Landkarte, auf welcher die Auswirkungen des Klimawandels deutlich werden, zu erstellen. Diese könnte dabei wie folgt aussehen: Climate Central.
Auf diesen Karten, die Ende Oktober veröffentlicht wurden, ist demnach zu sehen, welche Gebiete künftig wegen eines steigenden Meeresspiegel bedroht sein sollen, ab 2050 regelmäßig überflutet zu werden. Neben der Nordseeküste von Schleswig-Holstein und Niedersachsen könnten Hamburg und Bremen ebenfalls unter Wasser stehen, heißt es in verschiedenen Meldungen dazu. Auch in sozialen Medien wurden Screenshots der Karten geteilt - oft mit dem Hinweis, hier sei zu sehen, welche katastrophalen Folgen der Klimawandel in Europa haben werde. [9]
Gruppenmitglieder
[Bearbeiten]- David Spang
- Katharina Müller
- Zoe Richtscheid
- Anna Braun
Softwarenutzung
[Bearbeiten]- Geogebra
- Libre Office Calc
- JSON 3D Editor for Aframe
Quellennachweise
[Bearbeiten]- ↑ https://www.fr.de/rhein-main/viel-wasser-verbraucht-11322878.html (Stand: 25.01.2023)
- ↑ https://coastal.climatecentral.org/map/4/26.1495/44.776/?theme=sea_level_rise&map_type=coastal_dem_comparison&basemap=roadmap&contiguous=true&elevation_model=best_available&forecast_year=2100&pathway=rcp85&percentile=p95&refresh=true&return_level=return_level_1&rl_model=gtsr&slr_model=kopp_2017 (Stand: 26.01.2023)
- ↑ https://www.ardalpha.de/wissen/umwelt/klima/klimawandel/eisschmelze-eis-polkappen-antarktis-arktis-100.html (Stand: 26.01.2023)
- ↑ https://www.quarks.de/umwelt/klimawandel/was-passiert-wenn-der-meeresspiegel-steigt/ (Stand: 26.01.2023)
- ↑ https://www.umwelt-im-unterricht.de/hintergrund/das-wasser-der-welt-eine-geteilte-ressource/ (Stand: 25.01.2023)
- ↑ https://www.cipra.org/de/news/1277 (Stand: 26.01.2023)
- ↑ https://www.wwf-junior.de/tiere/elefanten-steckbriefe (Stand: 27.01.2023)
- ↑ https://argentinien.de/perito-moreno-gletscher/ (Stand: 11.02.2023)
- ↑ https://www.tagesschau.de/faktenfinder/klimawandel-ueberflutungen-101.html (Stand: 12.02.2023)








































![{\displaystyle V=(d\cdot {\frac {5}{3}}\cdot {\sqrt[{3}]{16,86}})^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/626e8f4260830af9545481cb25fcd44ebf9a7f1f)



































![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
![{\displaystyle [a,b]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a659536067aaaac2db1c44613a09a715f0cf7246)
![{\displaystyle x_{0}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06636653315ee7c3b5dc9bdb6ac3fb8cccadc145)
![{\displaystyle F\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/22aae183016ffbb759663208b693d6a28be4e69e)


![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)

![{\displaystyle \int _{a}^{b}f\left(x\right)dx=\left[F(x)\right]_{a}^{b}=F\left(b\right)-F\left(a\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e63f62d4c55d7fe69c3a69dfacb707cb72e0cef7)
![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)























![{\displaystyle [0.75;1.2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/441c3533a62a627fcc160633a837c3de246fb313)







![{\displaystyle {\sqrt {\sqrt {\frac {g}{\pi }}}}={\sqrt[{4}]{\frac {g}{\pi }}}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5c50f77a402e3af9ef2478b306536ac4108668a)





![{\displaystyle a={\sqrt[{4}]{\frac {g}{\pi }}}={\sqrt[{4}]{\frac {3,841}{\pi }}}=1,051}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e495204cff9deba78e251bac6ec0d5a826b61194)




















![{\displaystyle <=>{\sqrt[{4}]{\frac {0,92\cdot g}{4\cdot \pi }}}=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acb89a766ddbb44e702f212f744e4af34f84a157)











![{\displaystyle b={\sqrt[{4}]{\frac {0,92\cdot g}{4\cdot \pi }}}=92,50\longrightarrow a=130,81}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1534ccc2acb62da099ad68a3c945ab24f54cb339)
