Kurs:Mathematische Modellbildung/Themen/Volumenschätzung und Verbrauch von Ressourcen/Modellierungszklus 1

1. Ziel der Modellierung

In dieser Modellierung soll zunächst das Gewicht eines Elefanten bestimmt werden.

Um die Modellierung im Schulalltag passend einzubetten, wäre ein Wandertag in den Zoo anzuraten. In einer der folgenden Stunden könnte auf diesem Zoobesuch mit einer Textaufgabe zur Gewichtsfrage eines Elefanten aufgebaut werden.

1.1 Beispiel einer Textaufgabe

"Der Landauer Zoo hat ein Elefantengehege gebaut. Im Elefantengehege ist das Wasserbecken mit einer großen Glasscheibe zu den Besuchern hin abgetrennt, sodass die Besucher den Elefanten beim schwimmen und baden zuschauen können.

a) (Modellierungszyklus 1 - Sekundarstufe I) Um möglichst wenig Wasser zu verschwenden, wollen die Tierpfleger wissen, wieviel Wasser sie in das Becken einfüllen können ohne den Elefanten ihren optimalen Badespaß zu vermiesen, aber auch kein Wasser verloren geht, wenn es über den Beckenrand schwappt. Da die Elefantenwaage momentan noch nicht funktionstüchtig ist, müssen sie das Gewicht durch mathematische Rechnungen näherungsweise bestimmen. Berechne zunächst das Gewicht eines Elefanten anhand des vorgegeben Modells (Modell vgl. weiter unten in der Durchführung). Für fleißige: Finde eine Formel, die das Gewicht verschieden großer Elefanten angeben kann.

b) (mögliche Folgeaufgabe) Das Becken des Elefanten hat die Form eines Prismas um den Elefanten den Einstieg zu erleichtern. Das Becken ist 12 Meter lang und 8 Meter breit. An der tiefsten Stelle ist das Becken 5 Meter tief. Bestimme die Änderung des Wassers, wenn ein Elefant im Becken ist.

c) (Modellierungszyklus 2 - Sekundarstufe II) Um zu verhindern, dass die Zuschauer von dem vergnügten Elefanten zu nass gespritzt werden, möchte der Zoo die Glasscheibe zum Zuschauerbereich erhöhen. Um die Höhe der Glasscheibe zu bestimmen wird die Höhe der Welle gesucht, die an das Glas anschlägt und hochschwappt. Folgende Funktion für die Wellendarstellung sei gegeben: ("Funktion")

d) (Modellierungszyklus 3 - Uniniveau) ...

2. Mathematische Lernvoraussetzung

Zur Berechnung des Gewichts können folgende Lerninhalte vorausgesetzt werden: Auf- und Umstellung einer Formel, Bedeutung von Größen sowie die Bekanntheit verschiedener geometrischer Körper und deren Formeln zur Volumenberechnung.

Zur Approximation des Volumens eines Elefanten benötigen wir die folgenden Formeln der grundlegenden geometrischen Körpern:

Figur	Volumen	Schaubild
Ellipsoid	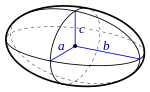$V={\frac {4}{3}}\pi abc$
Zylinder	$V=r^{2}\cdot \pi \cdot h$
Kegel	$V={\frac {1}{3}}\cdot \pi \cdot r^{2}\cdot h$

2.1 Einordnung in den schulischen Rahmenlehrplan

3. Vorgehensweise

Zunächst wollen wir das Gesamtgewicht eines Elefanten anhand des Volumens der einzelnen Körperteile bestimmen. Dazu nehmen wir verschiedene geometrische Körper zur Annäherung der einzelnen Körperteilen des Elefanten an.

Der Körper und der Kopf können somit durch ein Ellipsoid angenähert werden. Zur Darstellung der Beine, des Schwanzes und einem Teil des Rüssels kann die geometrische Form des Zylinders verwendet werden. Den anderen Teil des Rüssels kann mit einem Kegel angenähert werden.

Die Ohren werden hier wegen des geringen Gewichts im Gegenteil zum eigentlichen Körper vernachlässigt. Hieraus wird ein beispielhaftes Modell in JSON 3D Editor for AFrame erstellt. Anhand dieser Darstellung werden die Parameter der einzelnen geometrischen Körper bestimmt. Durch Ausrechnen der Formeln erhält man das Volumen der einzelnen Körper die in Summe das Gesamtvolumen eines Elefanten ergeben. Anhand dessen kann man die Wasserverdrängung in einem Wasserbecken ermitteln.

In einem zweiten Schritt ist es Möglich dieses Vorgehen so zu optimieren, dass man eine Formel herleitet, die von einer einfach zu bestimmenden Messung abhängt. Und man so das Gewicht von verschiedenen Elefanten bestimmen kann.

4. Durchführung

4.1 Größenangaben eines Elefanten

Die Größenangaben oder Schätzungen, um ein geeignetes Modell zu erstellen, ergeben sich idealerweise aus dem Biologieunterricht der Sekundarstufe I oder können auf der Internetseite (https://www.wwf-junior.de/tiere/elefanten-steckbriefe) nachgeschaut werden. Genauso können Bilder von Elefanten zur Abschätzung der Größenverhältnisse genutzt werden.

4.2 Modellierung des Elefanten in JSON 3D Editor for AFrame

Zu Beginn der Modellierung des Elefanten in JSON 3D Editor wurde der Rumpf und der Kopf durch ein Ellipsoid bestimmt. Dabei wurde der Mittelpunkt des Körper-Ellipsoids als Mittelpunkt des Rumpfes des Elefanten festgelegt. Die Beine wurden mithilfe eines Zylinders angenähert und jedes Bein des Elefanten ist gleichweit von dem Mittelpunkt des Rumpfes entfernt. Außerdem ist das vordere, linke Bein das Spiegelbild des vorderen, rechten Beins gespiegelt an der z-Achse.

Der nebenstehende Screenshot dient zur besseren Veranschaulichung der Erstellung des Elefanten in JSON 3D Editor for AFrame.

4.3 Ellipsoid (Körper)

Folgende Werte sind in Längeneinheiten zu betrachten.

Länge Elefant: $l=2\cdot 1,25$ $\Rightarrow$ $b={\frac {1}{2}}\cdot l=1,25$

Breite Körper: $b=2\cdot 4$ $\Rightarrow$ $a={\frac {1}{2}}\cdot b=4$

Höhe Köper: $h=2\cdot 1,25$ $\Rightarrow$ $c={\frac {1}{2}}\cdot h=1,25$

Volumen Körper: $V_{K{\ddot {o}}rper}={\frac {4}{3}}\cdot \pi \cdot 1,25\cdot 4\cdot 1,25=26,18$

4.4 Ellipsoid (Kopf)

Länge Kopf: $l=2\cdot 0,85$ $\Rightarrow$ $b={\frac {1}{2}}\cdot l=0,85$

Breite Kopf: $b=2\cdot 0,75$ $\Rightarrow$ $a={\frac {1}{2}}\cdot b=0,75$

Höhe Kopf: $h=2\cdot 0,75$ $\Rightarrow$ $c={\frac {1}{2}}\cdot h=0,75$

Volumen Körper: $V_{Kopf}={\frac {4}{3}}\cdot \pi \cdot 0,85\cdot 0,75\cdot 0,75=2,003$

4.5 Zylinder (Beine)

Radius Bein: $r=0,3$

Höhe Bein: $h=2\cdot 1,5=3$

Volumen Bein: $V_{Bein}=0,3^{2}\cdot \pi \cdot 3=0,848$

4.6 Dreieck (Ohr)

Das Ohr wurde in Aframe als Fläche angenommen. Daraus folgt für das Volumen des Ohres $V_{Ohr}=0$ . Diese Annahme wurde getroffen, da sich die Volumina in dem Modell teilweise überschneiden und die Fläche ausgleichen.

4.7 Zylinder (Rüssel)

Der Rüssel des Elefanten setzt sich aus zwei Rüsselteilen zusammen.

Radius Rüssel: $r=0,1+0,1=0,2$

Höhe Rüssel: $h=(2+0,2)\cdot 2=4,4$

Volumen Rüssel: $V_{R{\ddot {u}}ssel}=0,2^{2}\cdot \pi \cdot 4,4=0,553$

4.8 Zylinder (Schwanz)

Radius Schwanz: $r=0,5$

Höhe Schwanz: $h=1,5\cdot 2=3$

Volumen Schwanz: $V_{Schwanz}=0,5^{2}\cdot \pi \cdot 3=2,356$

4.9 Gesamtvolumen des modellierten Elefanten

Alle Volumina der jeweiligen Körperteile des Elefanten summieren sich zum Gesamtvolumen.

 $V_{Gesamt}=V_{K{\ddot {o}}rper}+V_{Kopf}+4\cdot V_{Bein}+V_{R{\ddot {u}}ssel}+V_{Schwanz}=31,94$

4.10 Problematik der erhaltenen Zahl

Was bedeutet die Zahl im Zusammenhang zu dem gesuchten Volumen eines Elefanten?

31,94 ist das Volumen unseres modellierten Elefanten in LE³. Dieser Wert kann mittels Dreisatz in das Gewicht eines Elefanten mit einem vorgegeben Fußdurchmesser umgewandelt werden:

geh.: Fußdurchmesser d=30cm, Modellfußdurchmesser m=0,6LE

Fehler beim Parsen (Syntaxfehler): {\displaystyle \text{geg.: Fußdurchmesser: d=30cm}, \text{Modellfußdurchmesser: m=0,6}\\  30cm=0,6LE \\ \Leftrightarrow 50cm=1LE\\\Leftrightarrow 158,7cm=3,194 LE\\\Leftrightarrow 3.996.969m^{3}=31,94LE^{3}}

geg.: Fußdurchmesser  $d=30cm$ , Modellfußdurchmesser  $m=0,6$ 
 $30cm=0,6LE\Leftrightarrow 50cm=1LE\Leftrightarrow 158,7cm=3,194LE\Leftrightarrow 39996969m^{3}=31,94LE^{3}$

Man kann durch folgende Formel aufstellen : ... Der Vorfaktor um ein geeignetes Gewicht zu erhalten, funktioniert nur für diesen Fuß und dieses Gewicht. Das liegt an dem funktionalen Zusammenhang. Hier liegt eine lineare Funktion vor. Wenn ich die große des Fußabdrucks ändere weiche ich von der ursprünglichen Funktion ab und treffe sie nur in diesem einen fall mit d=30cm. Wir möchten nun aber eine universelle Formel zur Berechnung des Gewichts verschiedener Elefanten haben.

5. Bewertung und Optimierung

Die Berechnung des Gewichts, durch die Darstellung verschiedener geometrischer Körper ist durch die Menge an Zahlen die man dazu braucht äußerst aufwendig und für den allgemeinen Gebrauch zu aufwendig. Abhilfe könnte eine Formel schaffen, die den Durchmesser eines Fußabdrucks in Beziehung zum Volumen des gesamten Elefantenkörpers setzt.

Die Formel kann wie folgt ermittelt werden: (vgl. dazu die Abbildung in JSON 4A Frame)

.-.

Die Anwendung dieser absolut kürzeren Formel ist bedeutend einfacher als die Summe der einzelnen Volumina der Körperteile.

Im nachfolgenden Bild ist die Anwendung der Formel beispielhaft erkennbar:

Die Tabelle (vgl. Bild rechts) zeigt die Überprüfung der oben errechneten Formel zur Bestimmung des Gewichts durch den Fußabdruck. Um diese Formel zu überprüfen, wurden 51 Zufallszahlen zwischen 25 und 45 cm Fußdurchmesser durch den Excelbefehl: =Zufallsbereich(25;45) generiert. Die Begrenzung ergibt sich daraus, dass die Fußgröße eines kleinen Elefanten auf rund 25 cm geschätzt wurde, sowie die eines sehr großen und ausgewachsenen Elefanten auf 45cm (Werte können sowohl bei einem Wandertag im Zoo ermittelt oder erfragt werden, als auch im Internet nachgeschaut werden).

In der zweiten Spalte wurde die errechnete Formel eingeben und das d mit der jeweils vorigen Zelle. Die ursprüngliche Formel wurde um die Division durch 1.000.000 um Kubikzentimeter (Einheit der oben errechneten Formel)ergänzt um das Gewicht direkt in Tonnen angeben zu können. (z.B.: d=45 cm --> 70,1*45^3/1.000.000=6,388t)

Um den Verlauf des Graphen, der Entwicklung des Fußdurchmessers zum errechneten Gewicht eines Elefanten, besser erkennen zu können, wurde ebenfalls in Ecxel das Diagramm (rechts) erstellt. Wie im vor hinein vermutet, verläuft der Graph exponentiell. Durch drücken der "Löschtaste" in der erstellten Exceldatei, ergeben sich immer neue Zufallswerte die alle auf diesem Graph liegen.

Der Einfachheit halber, lässt sich der Durchmesser des Elefantenfußes im Unterricht durch ablesen in sandigem Boden im Zoo oder, mit der Erlaubnis des Zoos und unter Aufsicht des Fachpersonals durch anfertigen eines Kunstdrucks mit Farbe auf auf Papier im Rahmen des Faches Bildende Kunst.

6. Quellenangaben

Gewichtsangaben eines Elefanten: https://www.wwf-junior.de/tiere/elefanten-steckbriefe