Kurs:Räumliche Modellbildung/Gruppe 1

Gruppenseite - NWG

Diese Seite enthält die gesammelten Materialien der Gruppe 1 - NWG für die Portfolioprüfung.

• COVID-19/Mathematische Modellbildung

Teilnehmer-innen

• Geiß, Annika
• Nebel, Ve
• Wolf, Sarah

Ziel der Veranstaltung

Das Modul M11: Entwicklung der Mathematik in Längs- und Querschnitten unterteilt sich in zwei Teilbereiche, einmal die diskreten Prozesse (Herr Niehaus) und einmal die Kontinuierlichen Diffusionsprozesse (Frau Hundertmark). Beide dienen am Ende einer Modellierung der COVID-19-Pandemie. In beiden Teilen wurde sowohl die zeitliche als auch die räumliche Betrachtung eingebaut.

Diskrete Diffusionsprozesse (Niehaus)

Thema und Ziel der Modellierung

In der folgenden Modellierung soll zunächst mithilfe des sogenannten SIR-Modells (siehe Kompartimentmodelle) und danach mithilfe eines Schachbrettmusters einer 10x10-Matrix und einer Transportmatrix, die Verbreitung des Corona-Virus sowohl räumlich als auch zeitlich implementiert werden. Die Modellierung erfolgt mittels CoCalc, sodass die Modelle als Gruppenarbeit mit Octave implementiert werden können.

Arbeitsauftrag 1: SIR-Modell

Versuch 1: Transportmatrix [1]

Festlegung der Werte zum Startzeitpunkt

Betrachtet wird das Beispiel Landau. Somit ergeben sich für S (Susceptible), I (Infected) und R (Removed) zum Zeitpunkt T₀ vor der Infektion folgende Werte:

$S=46677$
$I=0$
$R=0$

Der Vektor T₀ setzt sich damit aus S,I und R zusammen und zeigt den Startzustand an.

Erstellen der Transportmatrix

Die Transportmatrix gibt den Verlauf des Virus pro Tag an. Wir nehmen an, dass während der Krise 98 Prozent der infizierbaren Einwohner empfänglich für den Virus bleiben, während sich 2 Prozent wirklich infizieren. Von den infizerbaren Einwohnern wird keiner resistent. Betrachten wir nun die Infizierten. Hier nehmen wir an, dass 70 Prozent infiziert bleiben und 30 Prozent immun gegen den Virus werden.Bei den immunisierten Einwohnern nehmen wir an, dass diese sich nicht infizieren können sondern immun bleiben.

Somit ergibt sich folgende Transportmatrix $A$:

${\begin{pmatrix}0,98&0&0\\0,02&0,7&0\\0&0,3&1\end{pmatrix}}$

Beispielsweise beträgt der Anteil an Empfänglichen, welche infiziert werden 0,02, also 2 %.

Anwendung des Virus auf die Stadt Landau

Mit Hilfe einer Schleife (50 Tage) wird der Vektor $T_{i}$, mit $S_{i}$, $I_{i}$ und $R_{i}$, täglich mit der Transportmatrix (in diesem Fall$A$) multipliziert.

for  $i=1:50$
  $T_{i}=A^{i}*T_{0}$
  $S_{i}=T_{i}(1,1)$
  $I_{i}=T_{i}(2,1)$
  $R_{i}=T_{i}(3,1)$
 hold on
  plot (i, Si, 'b')
  plot (i, Ii, 'r')
  plot (i, Ri, 'g')
  legend ("Succeptible","Infected","Recoverd" )
 hold off
endfor 

Graphische Darstellung: SIR-Modell über eine Transportmatrix

Da man den genauen Verlauf der Infizierten im oberen Graphen nicht genau sehen kann, haben wir ihn in unterem Graphen neu geplottet.

Verbesserungsideen

Bemerkung

Im Rahmenlehrplan Mathematik Rheinland-Pfalz sind Matrizen in den Wahlpflichtgebieten der Oberstufe vorgeschrieben. Im Grundfach gibt es das Wahlpflichtgebiet "Matrizen in der praktischen Anwendung", in welchem sich eine solche Modellierung durchaus eignet.

Versuch 2: Funktionen [2]

Im zweiten Versuch soll der Verlauf der Infizierungen mehr einer Glockenkurve gleichen. Deshalb wird das Modell verbessert, indem wir anstelle einer Transportmatrix Funktionen für S, I und R erstellen, die den Verlauf der Pandemie möglichst gut abbilden.

Definition der Parameter

* Infektionsrate: $beta=0.3219$
* Genesungsrate: $gamma=0.1$
* Anzahl der Tage: $N_{t}=160$

t = linspace(0, N_t, N_t+1);

Erstellung der Vektoren

In diesem Schritt werden jeweils Vektoren für S, I und R erstellt. Es handelt sich hierbei um Spaltenvektoren, die alle mit 0 versehen sind und die Dimension N_t+1 besitzen.

$S=$zeros$(N_{t}+1,1)$;
$I=$zeros$(N_{t}+1,1)$; 
$R=$zeros$(N_{t}+1,1)$;

Bestimmung der Anfangswerte

Wir betrachten an dieser Stelle die Einwohnerzahl für die Stadt Landau (46677). Die Anfangswerte sehen dann wie folgt aus (relativer Anteil):

$S(1)=1$;
$I(1)=0.00002142$;    %relativer Anteil eines Infizierten Einwohners 
$R(1)=0$;

Zeitschleife

Wir lassen nun eine Zeitschleife über die Anzahl der festgelegten Tage 1 bis 160 laufen und implementieren für S, I und R jeweils Funktionen, welche den Wechsel von S nach I, I nach R usw. beschreiben. Für die erste Funktion betrachten wir die Anzahl der Infizierbaren am Tag n+1. Dafür benötigen wir die Anzahl der Infizierbaren am Tag zuvor, also am Tag n. Da die Anzahl von S abnimmt muss nun die Anzahl der Infizierten subtrahiert werden. Dies erfolgt durch die Multiplikation von S mit I und der Infektionsrate beta. Die Multiplikation von S und I beschreibt die Anzahl der Möglichkeiten, sich bei einer gewissen Anzahl von Menschen zu infizieren (vgl. Kombinatorik). Die Anzahl der Infizierten, welche in der ersten Funktion abgezogen wurden, werden in der zweiten Funktion dazu addiert, da die Zahl der Infizierten ansteigt. Hinzu kommt bei I, dass diejenigen, die wieder gesund sind, von der Anzahl der Infizierten abgezogen werden und in der dritten Funktion bei R dazu addiert werden. Hier wird also die Genesungsrate gamma benötigt, um den Anteil von Genesenen der Infizierten zu berechnen. So findet ein Wechsel zwischen S, I und R statt.

for  $n=1:N_{t}$
 $S(n+1)=S(n)-beta*S(n)*I(n)$
 $I(n+1)=I(n)+beta*S(n)*I(n)-gamma*I(n)$
 $R(n+1)=R(n)+gamma*I(n)$
endfor 

Graphische Darstellung: SIR-Modell über Funktionen

hold on
 plot(t,S,'b');
 plot(t,I,'r');
 plot(t,R,'g');
 axis([0 160 0 1.03]);
 legend ("Succeptible","Infected","Recoverd","location","east" )
hold off

Der dargestellte Graph zeigt den Verlauf unseres SIR-Modells. Die Kurve der Infizierten (rot) gleicht einer Glockenkurve und erreicht nach ca. 30 Tagen ihr Maximum.

mögliche Änderungen

Verbesserungsideen

• unterschiedlich lange Genesungsraten
• unterschiedliche Infektionsraten (angepasst an die Maßnahmen, z.B. Lockdown)
• räumliche Betrachtung

Arbeitsauftrag 2: Schachbrettmuster [3]

Im folgenden Modell soll mithilfe eines Schachbrettmusters einer 10x10-Matrix und einer Transportmatrix, die Verbreitung des Corona-Virus sowohl räumlich als auch zeitlich implementiert werden.

Erzeugung des Schachbrettmusters

Im ersten Schritt erzeugen wir ein Schachbrettmuster einer 10x10-Matrix. Anschaulich und in der realen Situation stehen die einzelnen Knoten des Schachbrettes für einen Ort oder zum Beispiel für einen Flughafen.

Schachbrettmuster einer 10x10 Matrix

Nx=10;
Ny=10;
x=[1:Nx];
y=[1:Ny];
[x,y]=meshgrid(x,y);

figure (1)
hold on;
plot (x,y,'*k')
axis([1 10 1 10]);
hold off;

SIR: Anfangswerte generieren

Nun müssen für jeden Gitterpunkt Anfangswerte für S, I und R festgelegt werden. Dazu werden die Anfangswerte für S zufällig gewählt. Für die Infizierten soll eine Matrix vorliegen die überall Nulleinträge besitzt, außer einem einzigen Wert. In diesem Ort beginnt die Infizierung. Die R-Anfangsmatrix ist eine Nullmatrix, da noch niemand die Infizierung überstanden hat.

$S_{0}=$round(rand$(10)*1000000)$
$I_{0}=$round(ones$(10).*{\begin{pmatrix}0&0&0&0&0&0&1&0&0&0\end{pmatrix}}).*{\begin{pmatrix}0\\0\\0\\0\\0\\0\\1\\0\\0\\0\end{pmatrix}})$ 
$R_{0}=$round(zeros$(10))$

${\begin{aligned}{\text{S0}}&=\\\\&\ {\begin{array}{r}3779&41440&90596&43113&81765&38178&99925&2173&22896&43216\\76583&99579&7898&54721&39423&67052&78157&26324&65523&22073\\3885&17505&31736&28836&36290&40688&60741&34663&27654&16019\\38235&69820&35272&87728&68645&26161&52232&10297&4138&83877\\54132&76714&32345&47613&82820&60987&51033&55658&14414&52942\\12409&86106&89868&23896&4192&73200&33384&91911&11533&82639\\52091&13310&43725&79233&62838&99455&49679&9221&58318&69665\\42973&58542&6601&87115&81938&1226&5665&72532&26392&20705\\16438&75787&41476&84899&12281&61524&40631&2858&6701&2984\\78087&55499&28406&42280&65653&44141&91851&70508&47556&73411\end{array}}\end{aligned}}$ ${\begin{aligned}{\text{I0}}&=\\\\&\ {\begin{matrix}0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&1&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\end{matrix}}\end{aligned}}$ ${\begin{aligned}{\text{R0}}&=\\\\&\ {\begin{matrix}0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\\0&0&0&0&0&0&0&0&0&0\end{matrix}}\end{aligned}}$

Gesamtanzahl der einzelnen Orte werden bestimmt.

for a=1:10
for b=1:10
G(a,b)=S0(a,b)+I0(a,b)+R0(a,b);
endfor
endfor

Von S,I und R werden relative Anteile zum weiterrechnen erstellt.

S0=S0./G;
I0=I0./G;
R0=R0./G;

Nun soll die zeitliche Änderung betrachtet werden.

SIR: Funktionen einbauen

Im folgenden werden für die drei Angfangsmatrizen jeweils neue Matrizen für die folgenden Tage berechnet. Dies kann man sich dann als eine 3D-Matrix vorstellen. Jeder weitere Tag bildet eine neue Matrix, die auf die vorherigen "gelegt" wird. Das ganze muss einmal für die Succesible, einmal für die Infected und schließlich für die Removed durchgeführt werden.

Definition der Parameter

* Anzahl der Tage: $N_{t}=20$
* Infektionsrate: $beta=0.5219$
* Genesungsrate: $gamma=0.08$

Aufstellung der Funktionen

Die Funktionen entsprechen denen, die auch im Arbeitsauftrag 1 verwendet wurden. Eine solche Implementierung kann folgendermaßen aussehen:

Sx=S0;
Ix=I0;
Rx=R0;
for t=1:N_t
   Sx=Sx-beta*Sx.*Ix;
   Ix=Ix+beta*Sx.*Ix-gamma*Ix;
   Rx=Rx+gamma*Ix;
   S=round(Sx.*G);
   I=round(Ix.*G);
   R=round(Rx.*G);
 hold on
 plot(t,S(7,7),'b',t,I(7,7),'r',t,R(7,7),'g',t,S(1,1),'bd',t,I(1,1),'rd',t,R(1,1),'gd',t,S(3,4),'bs',t,I(3,4),'rs',t,R(3,4),'gs')
 legend ("S (7,7)  ","I (7,7)  ","R (7,7)  ","S (1,1)  ","I (1,1)  ","R (1,1)  ","S (3,4)  ","I (3,4)  ","R (3,4)  ","location","southeast" )
endfor

Plots für 3 Orte

Transportmatrix

Zufällige Transportmatrix

Da für die Orte eine 10x10 Matrix gewählt wurde, muss für die Transportmatrix eine 100x100 Matrix generiert werden. Zunächst soll diese zufällig gewählt werden. Dabei muss aber die Summe der einzelnen Spalten 100% bzw. 1 ergeben da von einem Ort nicht mehr als 100% der Personen existieren.

${\begin{array}{r}0.0029645576&0.0186806020&0.0115510975&0.0038690357&0.0120527028&\\0.0145219023&0.0114634808&0.0048356911&0.0123540463&0.0057008587&\\0.0120104752&0.0002135190&0.0185543072&0.0082393831&0.0034665799&\\0.0186904996&0.0002094063&0.0179701547&0.0197176007&0.0053494958&\\0.0164324725&0.0088613570&0.0062407924&0.0168407343&0.0200401271&\\0.0133403514&0.0105458314&0.0115253475&0.0158437097&0.0049620685&\\0.0161884629&0.0011923745&0.0019497951&0.0116370675&0.0052994212&\\0.0088320056&0.0106939930&0.0034806168&0.0165959163&0.0178774891&\\0.0005707920&0.0088628687&0.0111539823&0.0181160896&0.0051886704&\\0.0073511810&0.0162083292&0.0000570935&0.0033836295&0.0058084401&\\0.0068639620&0.0127085878&0.0057059106&0.0140611505&0.0189740006&\\0.0083710869&0.0056314259&0.0168502342&0.0120188163&0.0112536046&\\0.0162861988&0.0109797986&0.0068640307&0.0193800996&0.0034605572&\\0.0090803988&0.0146059182&0.0190100647&0.0088732884&0.0025645727&\\0.0046820570&0.0075358754&0.0022364862&0.0093404441&0.0002879530\end{array}}$

for $j=1:100$
   $x=$rand$(100,1)$;
   $x=x/$sum$(x)$; 
   $T(1:100,j)=x$;
endfor

Anwendung auf Anfansmatrizen

Um die 100x100-Transportmatrix auf die 10x10-S₀-Matrix anwenden zu können, muss die S₀-Matrix in einen langen Vektor mit 100x1 umgeformt werden. Nach der Matrizenmultiplikation kann der entstandene Vektor wieder in eine 10x10-Matrix umgeformt werden.

Sx=S0;
Ix=I0;
Rx=R0;
 for t=1:N_t
   Sx=Sx-beta*Sx.*Ix;
   Ix=Ix+beta*Sx.*Ix-gamma*Ix;
   Rx=Rx+gamma*Ix;
   Sx=reshape(Sx,100,1);
   Sx=T*Sx;
   Sx=reshape(Sx,10,10);
   S=round(Sx.*G);
   Ix=reshape(Ix,100,1);
   Ix=T*Ix;
   Ix=reshape(Ix,10,10);
   I=round(Ix.*G);
   Rx=reshape(Rx,100,1);
   Rx=T*Rx;
   Rx=reshape(Rx,10,10);
   R=Rx.*G;
  hold on
  plot(t,S(7,7),'b',t,I(7,7),'r',t,R(7,7),'g',t,S(1,1),'bd',t,I(1,1),'rd',t,R(1,1),'gd',t,S(3,4),'bs',t,I(3,4),'rs',t,R(3,4),'gs')
  legend ("S (7,7)  ","I (7,7)  ","R (7,7)  ","S (1,1)  ","I (1,1)  ","R (1,1)  ","S (3,4)  ","I (3,4)  ","R (3,4)  ","location","southeast" )
 endfor

Plots für 3 Orte

Verbesserte Transportmatrix

Nun soll berücksichtigt werden, dass die meisten Menschen den Ort nicht wechseln. Dies entspricht der Diagonale auf der Transportmatrix. Dazu soll zunächst eine Matrix mit passenderen Werten erstellt werden, die im nächsten Schritt normiert wird, sodass die einzelnen Spalten der Matrix wieder 1 ergeben.

Für die Diagonale werden nun Werte zwischen 50 und 90 festgelegt.

$x=$rand$(1,100)*40+50$;
$v(1:100)=x$;          
$D=diag(v,0)$;

Dazu wird eine zweite Matix mit Werten zwischen 0 und 10 festgelegt. Alternativ hätte man die Werte hier auch kleiner wählen können.

B=rand(100,100)*10;

Die beiden Matrizen werden im nächsten Schritt addiert und anschließend normiert.

${\begin{array}{r}0.60999008744&0.00138479881&0.00401305211&0.00044698317&0.00246012890\\0.00169868305&0.63228661893&0.00383945012&0.00296569974&0.00597072136\\0.00580967449&0.00604640658&0.62739041874&0.00713924442&0.00309323581\\0.00466655264&0.00379375645&0.00036955497&0.61736443364&0.00103263484\\0.00665620798&0.00088243311&0.00561151725&0.00318886431&0.66220061985\\0.00503605231&0.00372589469&0.00764759528&0.00056010657&0.00271091672\\0.00067158108&0.00653913238&0.00428399407&0.00348056655&0.00344044172\\0.00072057776&0.00021624527&0.00066245180&0.00178163751&0.00476231060\\0.00040008491&0.00350108610&0.00247219739&0.00235955350&0.00337456177\\0.00656945435&0.00162275569&0.00763364405&0.00586140224&0.00501994659\\0.00660314274&0.00218224218&0.00472114802&0.00615499151&0.00348945574\\0.00307720025&0.00767247167&0.00745230541&0.00068888055&0.00716250951\\0.00582673448&0.00539452511&0.00613837243&0.00673362539&0.00304135557\\0.00278788495&0.00607230050&0.00584739347&0.00276247525&0.00430695428\\0.00246565542&0.00357726740&0.00558888292&0.00632216486&0.00741504525\\0.00255940957&0.00177055083&0.00295046221&0.00738431314&0.00453287733\\0.00302851771&0.00303909144&0.00597940848&0.00002860110&0.00418741117\end{array}}$

$C=D+B$;
for $n=1:100$
   $j=$sum$(C(:,n))$; 
   $X=(C(:,n)/j)$;
   $T_{neu}(1:100,n)=X$;
endfor

Anwendung auf Anfansmatrizen

Sx=S0;
Ix=I0;
Rx=R0;
for t=1:N_t
   Sx=Sx-beta*Sx.*Ix;
   Ix=Ix+beta*Sx.*Ix-gamma*Ix;
   Rx=Rx+gamma*Ix;
   Sx=reshape(Sx,100,1);
   Sx=Tneu*Sx;
   Sx=reshape(Sx,10,10);
   S=round(Sx.*G);
   Ix=reshape(Ix,100,1);
   Ix=Tneu*Ix;
   Ix=reshape(Ix,10,10);
   I=round(Ix.*G);
   Rx=reshape(Rx,100,1);
   Rx=Tneu*Rx;
   Rx=reshape(Rx,10,10);
   R=round(Rx.*G);
 hold on
 plot(t,S(7,7),'b',t,I(7,7),'r',t,R(7,7),'g',t,S(1,1),'bd',t,I(1,1),'rd',t,R(1,1),'gd',t,S(3,4),'bs',t,I(3,4),'rs',t,R(3,4),'gs')
 legend ("S (7,7)  ","I (7,7)  ","R (7,7)  ","S (1,1)  ","I (1,1)  ","R (1,1)  ","S (3,4)  ","I (3,4)  ","R (3,4)  ","location","southeast" )
endfor

Plots für 3 Orte

Transportmatrix mit Berücksitigung der Distanz

Für die Ortswechsel soll nun die Distanz der einzelnen Orte berücksichtigt werden. Je näher Orte aneinander liegen, desto eher findet ein Austausch statt. Eine Möglichkeit die Distanz zu berücksichtigen ist, diese reziprok in die Transportmatrix einzubauen. Dadurch folgt, je näher die Orte, desto größer der Wert in der Matrix. Damit jedoch nicht durch Null geteilt wird, wenn der Abstand eines Ortes zu sich selbst bestimmt wird, wird ${\frac {1}{1+dist}}$ eingesetzt.

Zunächst wird die Distanz in einer Funktion definiert.

function ret=norm(i,j);
       ret =sqrt(i^2+j^2);
endfunction

function dist=distanz(i,j,k,l);
       dist = norm(i-k,j-l);
endfunction

In einer Schleife wird nun ein Vektor XX gebildet, der die Distanz zwischen allen Punkten in der Form ${\frac {1}{1+dist}}$ enthält. Anschließend wird der Vektor in eine 100x100-Matrix überführt.

XX=0;

for i=1:Nx
  for  j=1:Ny
     norm(i,j);
     for  k=1:Nx
        for  l=1:Ny
            Xneu=(1/(1+norm(i-k,j-l)));
            XX=[XX Xneu];
        endfor
     endfor
  endfor
endfor
XX(2:10001);
XXX=reshape(XX(2:10001),100,100); 

${\begin{array}{r}0.0639758&0.0293422&0.0185205&0.0134418&0.0105881&0.0088234&\\0.0319879&0.0586844&0.0277808&0.0179224&0.0132351&0.0105881&\\0.0213253&0.0293422&0.0555615&0.0268835&0.0176469&0.0132351&\\0.0159939&0.0195615&0.0277808&0.0537671&0.0264703&0.0176469&\\0.0127952&0.0146711&0.0185205&0.0268835&0.0529406&0.0264703&\\0.0106626&0.0117369&0.0138904&0.0179224&0.0264703&0.0529406&\\0.0091394&0.0097807&0.0111123&0.0134418&0.0176469&0.0264703&\\0.0079970&0.0083835&0.0092603&0.0107534&0.0132351&0.0176469&\\0.0071084&0.0073356&0.0079374&0.0089612&0.0105881&0.0132351&\\0.0063976&0.0065205&0.0069452&0.0076810&0.0088234&0.0105881&\\0.0319879&0.0243079&0.0171695&0.0129177&0.0103337&0.0086802&\\0.0264996&0.0293422&0.0230143&0.0166149&0.0127191&0.0103337&\\0.0197696&0.0243079&0.0277808&0.0222710&0.0163595&0.0127191&\\0.0153704&0.0181345&0.0230143&0.0268835&0.0219287&0.0163595&\\0.0124877&0.0140991&0.0171695&0.0222710&0.0264703&0.0219287&\\0.0104895&0.0114549&0.0133488&0.0166149&0.0219287&0.0264703&\\0.0090326&0.0096219&0.0108453&0.0129177&0.0163595&0.0219287\end{array}}$

for n=1:100
 P=XXX(1:100,n)/sum(XXX(1:100,n));
 Tneu2(1:100,n)=P;
endfor

Anwendung auf Anfansmatrizen

Sx=S0;
Ix=I0;
Rx=R0;
for t=1:N_t
   Sx=Sx-beta*Sx.*Ix;
   Ix=Ix+beta*Sx.*Ix-gamma*Ix;
   Rx=Rx+gamma*Ix;
   Sx=reshape(Sx,100,1);
   Sx=Tneu2*Sx;
   Sx=reshape(Sx,10,10);
   S=round(Sx.*G);
   Ix=reshape(Ix,100,1);
   Ix=Tneu2*Ix;
   Ix=reshape(Ix,10,10);
   I=round(Ix.*G);
   Rx=reshape(Rx,100,1);
   Rx=Tneu2*Rx;
   Rx=reshape(Rx,10,10);
   R=round(Rx.*G);
 hold on
 plot(t,S(7,7),'b',t,I(7,7),'r',t,R(7,7),'g',t,S(1,1),'bd',t,I(1,1),'rd',t,R(1,1),'gd',t,S(3,4),'bs',t,I(3,4),'rs',t,R(3,4),'gs')
 legend ("S (7,7)  ","I (7,7)  ","R (7,7)  ","S (1,1)  ","I (1,1)  ","R (1,1)  ","S (3,4)  ","I (3,4)  ","R (3,4)  ","location","southeast" )
endfor

Plots für 3 Orte

Transportmatrix mit Berücksitigung der Infiziertenbewegung

Da sich die Infizierten kaum bewegen soll für die Infizierten die Zuhausebleibematrix und für beide anderen Gruppen die Distanzmatrix gelten (s.o.).

${\begin{array}{r}0.0639758&0.0293422&0.0185205&0.0134418&0.0105881\\0.0319879&0.0586844&0.0277808&0.0179224&0.0132351\\0.0213253&0.0293422&0.0555615&0.0268835&0.0176469\\0.0159939&0.0195615&0.0277808&0.0537671&0.0264703\\0.0127952&0.0146711&0.0185205&0.0268835&0.0529406\\0.0106626&0.0117369&0.0138904&0.0179224&0.0264703\\0.0091394&0.0097807&0.0111123&0.0134418&0.0176469\\0.0079970&0.0083835&0.0092603&0.0107534&0.0132351\\0.0071084&0.0073356&0.0079374&0.0089612&0.0105881\\0.0063976&0.0065205&0.0069452&0.0076810&0.0088234\\0.0319879&0.0243079&0.0171695&0.0129177&0.0103337\\0.0264996&0.0293422&0.0230143&0.0166149&0.0127191\\0.0197696&0.0243079&0.0277808&0.0222710&0.0163595\\0.0153704&0.0181345&0.0230143&0.0268835&0.0219287\end{array}}$

${\begin{array}{r}0.948850266372&0.001013550854&0.000868282200&0.000129565249&\\0.000159536828&0.940115778528&0.000060781347&0.000792339941&\\0.000028599445&0.000528718170&0.956839043908&0.000738232882&\\0.000824900769&0.000050046736&0.000396391855&0.944593411851&\\0.000624169755&0.000115683468&0.000792342776&0.000709492625&\\0.000890196010&0.000608938549&0.000294551621&0.001018323000&\\0.000454071023&0.000973882436&0.000263840266&0.000138081054&\\0.000825504848&0.001043283581&0.000428529882&0.000860224698&\\0.000116584021&0.000549162764&0.000267662808&0.000437187473&\\0.000796738578&0.000916046985&0.000533148238&0.000904167747&\\0.000204051030&0.000267521656&0.000564845326&0.000883089870\end{array}}$

Plots für 3 Orte

Weitere Vorgehensweise - Möglichkeiten

• Zeitschritte variieren (z.B. in jedem Zeitschritt, wöchentlich usw.)
• Reelle Orte und Distanzen einbauen

Skripte in Cocalc

A1:SIR-Modell über Transportmatrix [4]

A1:SIR-Modell über Funktionen [5]

A2:Schachbrettmuster [6]

Kontinuierliche Diffusionsprozesse (Hundertmark)

Thema und Ziel der Modellierung

Im folgenden werden verschiedenen Modelle auf die Corona-Situation angewendet. Die Berechnungen sollen möglichst aussagekräftige bzw. realistische Vorhersagen über die Verbreitung des Virus treffen.

1.Tutoriumsaufgabe: Kontaktmodell [7]

Das Kontaktmodell beschreibt die räumliche Ausbreitung einer Infektion durch direkten Kontakt von sich bewegenden Menschen. Ab einem gewissen Abstand erfolgt automatisch eine Infizierung.

Erstellung eines 20x20 Schachbrettmusters

Zunächst wird eine 20x20-Matrix erstellt, sowie einige Parameter festgelegt.

$Nx=20$;
$Ny=20$;
$g=0.5$;  %Bewegungsgeschwindigkeit 
$T=3$;    %Zeiteinheit 
$Zeitschritte=3$; %pro Zeiteinheit 
$dt={\frac {1}{Zeitschritte}}$; 
$x=[1:Nx]$;
$y=[1:Ny]$;
$[x,y]=$meshgrid$(x,y)$;

Damit dieses als Schachbrettmuster angezeigt wird, werden folgende Befehle benötigt. Hierbei werden die Matrixeinträge als Blaue Sterne festgelegt. Diese entsprechen jeweils einer realen Person, zunächst nur statisch, also ohne Bewegung.

Schachbrettmuster einer 20x20 Matrix

figure (1)
hold on;
 plot(x,y, '*b') ;
 axis([-5 25 -5 25]);
hold off;

Generieren einer Bewegung

Im nächsten Schritt soll die Bewegung generiert werden, damit sich die einzelnen Punkte des Schachbrettmusters (also Personen) bewegen. Die Bewegungsrichtung sowie die zurückgelegte Entfernung soll zufällig sein, was durch den Befehl "rand" gewährleistet wird.

Mit dem Befehl rand$(Ny,Nx)$ wird eine NyxNx-Matrix, also in unserem Fall eine 20x20-Matrix mit Werten zwischen 0 uns 1 erstellt. Durch Subtraktion von 0.5 werden die Zufallszahlen in das Intervall $]-0.5,0.5[$ verschoben. Somit wird die neue Position jeders Punktes durch Addition der Zufallszahl zwischen -0.5 und 0.5 zur ensprechenden x,y-Koordinate generiert und mit der Geschwindigkeit g skalliert.

Bewegung ohne Infizierten

neuPosX=x.+g.*rand(Ny,Nx)-0.5*g;
neuPosY=y.+g.*rand(Ny,Nx)-0.5*g;

Die neue Position wird jedoch nicht in einem Schritt erreicht. In jedem Zeitschritt $i$ wird nur der entsprechende Bruchteil $i*dt$ zur alten Position addiert. Daher muss eine Zeitschleife generiert werden.

 for i=1:T*Zeitschritte
  neuX=x.+1*(neuPosX.-x)*i*dt;   % dt = 1/Zeitschritte
  neuY=y.+1*(neuPosY.-y)*i*dt;

  figure (i+1)
  title (['t=' num2str(i·dt)])
  axis([-5 25 -5 25]);
  hold on;
   plot(neuX,neuY, '*b') ;
  hold off;
 endfor

Infizierter hinzufügen

Nun soll ein Infizierter hinzukommen. Dieser ist durch ein rotes Quadrat gekennzeichnet und wird zunächst in die Mitte des Schachbrettmusters gesetzt. Außerdem wird ein Ansteckungsradius als Abstandsschranke festgelegt.

Schachbrettmuster einer 20x20 Matrix mit einem Infizierten

$xInf=x(1,{\frac {Nx}{2}}\ );$
$yInf=y({\frac {Ny}{2}}\ );$
$IndInf2={\frac {Nx}{2}}\ ;$
$IndInf1={\frac {Ny}{2}}\ ;$
$IndInf1neu=IndInf1;$
$IndInf2neu=IndInf2;$
$radiusInf=0.80;$              %Ansteckungsradius

figure (11)
hold on;
 plot(x,y, '*b') ;
 plot(xInf,yInf, "sr")
 axis([-5 25 -5 25]);
hold off;

Bewegung mit Infiziertem

Bewegung mit Infiziertem

Die neue Position der einzelnen Individuen ist unabhägig von einer Infizierung und entspricht daher der normalen Generierung einer Bewegung.

neuPosX=x.+g.*rand(Ny,Nx)-0.5*g;
neuPosY=y.+g.*rand(Ny,Nx)-0.5*g;

Allerdings muss die Zeitschleife angepasst werden, da nicht nur in der Endposition, sondern in jedem Zeitschritt der Abstand zwischen den einzelnen Individuen überprüft werden muss. Ist dieser kleiner als der Ansteckungsradius, so wird die Infektion übertragen und es entsteht ein neuer Infizierter.

for  i=1:T*Zeitschritte
  neuX=x.+1*(neuPosX.-x)*i*dt;
  neuY=y.+1*(neuPosY.-y)*i*dt;
  figure (i+20)
  title(['t=' num2str(i*dt)])
  axis([-5 25 -5 25]);
   hold on
    plot(neuX,neuY, '*b');
       for  k1=1:length(IndInf1) 
        for  j=1:Nx
         for  l=1:Ny
           abstand=norm([neuX(l,j)-neuX(IndInf1(k1),IndInf2(k1)), neuY(l,j)-neuY(IndInf1(k1),IndInf2(k1))]);
             if  abstand<radiusInf1 %Abstand<Asteckungsradius?
               abstand;    
               plot(neuX(l,j),neuY(l,j), 'sr') %Färbe rot 
               k2=1;
                 while  k2 <=length(IndInf1)&&(l!=IndInf1neu(k2) || j!=IndInf2neu(k2)) % Überprüfen: Schon in Vektor der Infizierten enthalten?
                   k2=k2+1;
                 endwhile 
                   if   k2 >length(IndInf1)
                     IndInf1neu=[IndInf1neu l];
                     IndInf2neu=[IndInf2neu j];
                   endif  
              endif  
          endfor 
         endfor 
        endfor 
     IndInf1=IndInf1neu;
     IndInf2=IndInf2neu;
    hold off
  lengt=length(IndInf1);
endfor 

Änderung Ansteckradius

Radius größer

Im folgenden soll die Auswirkung eines veränderten Ansteckungsradius demonstriert werden. Dabei bleibt der Code der Implementierung gleich. Nur der Wert des Ansteckungsradius wird variiert.

• größerer Ansteckradius:

radiusInf1=0.95  %vorher 0.80

Radius kleiner

• kleinerer Ansteckradius:

radiusInf2=0.60

Ergebnis: An den Animationen auf der rechten Seite kann man erkennen, dass sich der Verlauf der Infizierungen deutlich verändert, sobald der Ansteckungsradius variiert wird. So zeigt sich zum Beispiel, dass sich bei einem größeren Ansteckungsradius mehr Menschen in kürzerer Zeit infizieren als bei einem kleineren Ansteckungsradius.

Änderung Bewegungsgeschwindigkeit

Geschwindigkeit höher

Ebenso soll der Einfluss der Bewegungsgeschwindigkeit demonstriert werden. Dazu werden folgende Veränderungen im Code vorgenommen:

• höhere Geschwindigkeit:

neuX=x.+5*(neuPosX.-x)*i*dt;
neuY=y.+5*(neuPosY.-y)*i*dt;  %vorher neuY=y.+1*(neuPosY.-y)*i*dt

Geschwindigkeit geringer

• niedrigere Geschwindigkeit:

neuX=x.+0.2·(neuPosX.-x)·i·dt;
neuY=y.+0.2·(neuPosY.-y)*i·dt;

Ergebnis:Auch hier kann man erkennen, dass die Veränderung der Bewegungsgeschwindigkeit Auswirkungen auf den Verlauf der Infizierung hat. Bei einer höheren Geschwindigkeit werden deutlich mehr Menschen infiziert. Bei geringerer Geschwindigkeit verläuft die Infizierung langsamer.

Änderung Bewegungsrichtung

Bewegungsrichtung

Richtungsänderung in jedem Zeitschritt

for  i=1:T*Zeitschritte
   x=neuX;
   y=neuY;
   neuPosX=x.+g.*rand(Ny,Nx)-0.5*g;
   neuPosY=y.+g*rand(Ny,Nx)-0.5*g;
   neuX=x.+1*(neuPosX.-x)*i*dt;
   neuY=y.+1*(neuPosY.-y)*i*dt;
   ...
endfor 

Um die Schritte besser nachvollziehen zu können werden Richtungspfeile angezeigt:

quiver(neuX,neuY,neuPosX.-x, neuPosY.-y)

Änderung Anfangsposition des Infizierten

Anfangsposition am Rand

• Rand:

xInf=x(1,Nx/2);
yInf=y(1);           %vorher yInf=y(Ny/2); 
IndInf2=Nx/2;
IndInf1=1;

Anfangsposition in der Ecke

• Ecke:

xInf=x(1,1);
yInf=y( 1);
IndInf2=1;
IndInf1=1;

Ergebnis: Je weiter die infizierte Person am Rand ist, desto weniger Menschen werden angesteckt. Je mehr Menschen sich um den Infizierten befinden, desto höher ist die Gefahr, dass diese infiziert werden.

Verbesserungsideen

• Wenn Abstand < Infektionsradius, folgt nur unter einer bestimmten Warscheinlichkeit eine Ansteckung

Vorteile dieses Modells

• Betrachtung der Verbreitung auf kleinstem Raum (Bsp: Supermarkt, Straße)

2.Tutoriumsaufgabe: Fundamentallösungen der Poisson und der Diffusionsgleichung [8]

Der folgenden Modellierung ist die räumliche Diffusion zu Grunde gelegt. Dies meint die zufällige Bewegung von Teilchen, sodass ein vorliegender Konzentrationsunterschied ausgeglichen wird und mit der Zeit eine vollständige Durchmischung eintritt. Mathematisch wird ein Diffusionsprozess folgendermaßen beschrieben: $\partial _{t}u(x,t)-div(c(x)\nabla u(x,t))=0$

Dabei ist

$u:\mathbb {R} ^{n}\times \mathbb {R} ^{+}\ \to \mathbb {R}$ die unbekannte Teilchenkonzentrationsdichte/Temperaturdichte und

$c:{\mathbb {R} }^{n}\to {\mathbb {R} }$ der ortsabhängige Diffusion-/Wärmeleitkoeffizient.

Teil 1: Stationäre Diffusion

Wird jedoch nur der stationäre Fall $u(x,t)=u(x)$, also der Gleichgewichtszustand betrachtet, so ist die Zeitableitung gleich Null. Gilt außerdem $c(x)=1$, so liegt die bekannte Laplace-Gleichung $\Delta u(x)=0$ vor.

Die in dieser Tutoriumsaufgabe verwendete Poisson-Gleichung entspricht der inhomogenen Laplace-Gleichung. Hier ist $f$ die Funktion der rechten Seite, welche die Dichtefunktion der Flussgeschwindigkeit in das System hinein beschreibt. Anders formuliert entspricht $f$ der kontinuierlichen Infektionsquelle, also einem oder mehreren Hotspots.

$$-\Delta u(x)=f(x)$$

Für die Modellierung muss vorrausgesetzt werden, dass $f$ einen kompakten (beschränkten)Träger inerhalb des Gebietes $D\subset \mathbb {R} ^{2}$ besitzt.

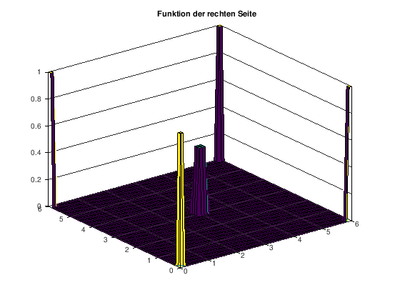
Funktion der rechten Seite

Zunächst wird die Funktion $f$ der rechten Seite definiert.

function wert=Quellfunktion(x,y)
 if sqrt((x.-6).^2+(y.-6).^2)<=0.15 wert=1;
   else wert=0;
   if sqrt((x.-6).^2+(y.-0).^2)<=0.15 wert=1;
    else wert=0;
     if sqrt((x.-0).^2+(y.-6).^2)<=0.15 wert=1;
    else wert=0;
     if sqrt((x.-0).^2+(y.-0).^2)<=0.15 wert=1;
    else wert=0;
     if sqrt((x.-3).^2+(y.-3).^2)<=0.15 wert=0.5;
    else wert=0;
 endif
 endif
 endif
 endif
 endif
endfunction

Definition des Gebietes

Im folgenden wird ein rechteckiges Gebiet $D\subset \mathbb {R} ^{2}$ mit Hilfe eines Gitters $G_{h}$ definiert, wobei die Schrittweite mit $h=0,03$ festgelegt wird.

step=0.1;
X=[0:step:6];
Y=[0:step:6];
[x,y]=meshgrid(X,Y);

Speichern der Funktionswerte von f in jedem Gitterpunkt

Auf dem definierten Gebiet soll nun die Infektionsquelle festgelegt werden. Dazu müssen die Funktionswerte von f in jeden einzelnen Gitterpunkt $f(x(j,i),y(j,i))$ der Matrix gespeichert werden.

for i=1:(length(X))    
 for j=1:(length(Y))
  f(j,i)=1*Quellfunktion(x(j,i),y(j,i)); 
 endfor  
endfor

Graphisch sieht dies nun folgendermaßen aus:

Die Abbildung zeigt in unserem Fall 4 Träger, also 4 Infektionsquellen, an denen kontinuierlich ein Stoff aus einer Quelle hinzugefügt wird. Übertragen auf die Corona-Ausbreitung finden wir hier 4 Hotspots von Infizierten vor.

Implementierung der Poisson-Gleichung

Die Lösung der Poisson-Gleichung $-\Delta u(x)=f(x)$ lässt sich mithilfe der Faltung der Fundamentallösung der Laplace-Gleichung $\Delta u(x)=0$ und der Funktion der rechten Seite berechnen.

$$u(x^{*})=(\Phi *f)(x^{*})=\int _{\mathbb {R} ^{2}}\Phi (x^{*}-x)f(x)dx=\int _{D}\Phi (x^{*}-x)f(x)dx=\int _{0}^{2}\int _{0}^{2}\Phi (x^{*}-x,y^{*}-y)f(x,y)dxdy$$

Die Fundamentallösung der Laplace-Gleichung für $\mathbb {R} ^{2}$ hat folgende Formel:

$$u(x)=\Phi (x):=-{\frac {1}{2\pi }}ln\|x\|$$

Zuerst werden die Werte der Fundamentalfunktion $\Phi$ für jeden Gitterpunkt $x(j,i),y(j,i)$ um ein festes $x^{*}\in D_{h}$ verschoben und in der Matrix 'phi' gespeichert.

Dazu wird $x^{*}$ als Matrix mit konstanten Einträgen durch Konstruktion einer Schleife definiert, damit die Differenz der Funktionsargumente als Differenz von Matrizen möglich ist.

Nun muss noch beachtet werden, dass $\Phi$ singulär wird (d.h. $\lim _{x\to 0}\Phi (x)=\infty$), wenn $x^{*}\equiv x$. Um diesen Punkt der Singularität auszuschneiden, setzen wir $\Phi (x^{*}-x)=0$ für $x^{*}\equiv x$. Durch die klein gewählte Schrittweite beeinflusst dies das Ergebnis kaum.

Das doppelte Integral kann mit der Trapezregel berechnet werden.

fori=1:(length(X)) 
 for j=1:(length(Y))
 xstar=x(j,i)*ones(length(Y),length(X));
 ystar=y(j,i)*ones(length(Y),length(X));
% Phi mit verschobenem Argument:
 phi=-log(sqrt((xstar.-x).^2+(ystar.-y).^2))/(2*pi);
 phi(j,i)=0;
% numerische Integration:
 I(j,i) = trapz(Y,trapz(X,phi.*f,2));
 endfor
endfor

Die Graphik dazu wird durch folgenden Befehl von Octave ausgegeben.

figure 1
meshc(x,y,I)
grid on
title ('Losung von Poissongleichung')
xlabel('x')
xlabel ('y')

Die Abbildung zeigt die Lösung der Poissongleichung, die durch doppelte Integration auf unserem Gebiet von 0 bis 2 entsteht. Diese beschreibt die Verteilung des Stoffes (ausgehend von unserer oben definierten Funktion der rechten Seite).

Teil 2: Instätionäre Diffusion

Weiterführend soll außerdem die instationäre Diffusion betrachtet werden. Dabei wird eine zeitabhängige Diffusion als Anfangswertproblem betrachtet. Mit einem konstanten Diffusionskoeffizienten $c(x)\equiv a\in \mathbb {R}$ folgt die homogene Differenzialgleichung $\partial _{t}u-a\Delta u=0,x\in \mathbb {R} ^{n},t\in \mathbb {R} ^{+}$, für welche eine spezielle Lösungsformel existiert:

$$u(x,t)=\Psi (x,t)={\frac {1}{(4\pi at)^{\frac {n}{2}}}}\exp \left(-{\frac {\|x\|^{2}}{4at}}\right),$$

wobei $\textstyle \|{x}\|^{2}=\sum _{k=1}^{n}x_{k}^{2}$ das Quadrat der euklidischen Norm von $x$ ist.

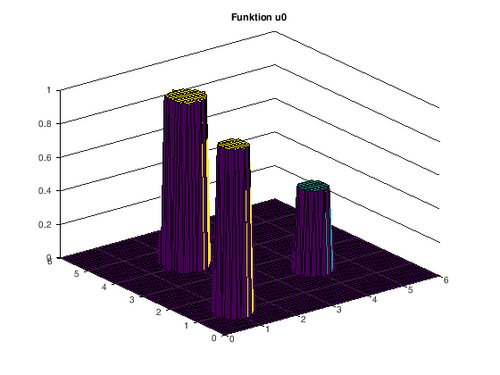
Anfangsfunktion

Zunächst wird eine neue Anfangsfunktion $u_{0}$ mit kompaktem Träger aufgestellt.

   function wert=Anfangslosung(x,y)
    if sqrt((x.-2).^2+(y.-4).^2)<=0.05 wert=1;
    else wert=0;
    if sqrt((x.-4).^2+(y.-2).^2)<=0.04 wert=0.5;
    else wert=0;
    if sqrt((x.-1).^2+(y.-1).^2)<=0.04 wert=1;
    else wert=0;
 endif
 endif
endfunction

Auch hier müssen die Funktionswerte von $u_{0}$ in jeden Gitterpunkt $u_{0}(x(j,i),y(j,i))$ der Matrix gespeichert werden.

 for i=1:(length(X)) 
 for j=1:(length(Y))
  u0(j,i)=1*Anfangslosung(x(j,i),y(j,i));
 endfor  
endfor

Zeitparameter

Im folgenden wird der Zeitrahmen festgelegt. Außerdem wird der Diffusionskoeffizient a festgelegt. Um zu verhindern, dass $\Psi$ singulär wird (d.h. $\lim _{x\to 0}\Psi (x)=\infty$), wählen wir $t_{0}>0$.

T=2;
Zeitschritte=2;
dt=1/Zeitschritte;
t0=0.001;
a=0.2;

Immplementieren der Lösungsformel

Ähnlich wie im stationären Fall kann die Lösung mithilfe einer Faltung der Fundamentallösung und der Anfangsfunktion $u_{0}$ berechntet werden.

$$u(x^{*},t)=(\Psi *u_{0})(x^{*},t)=\int _{\mathbb {R} ^{2}}\Psi (x^{*}-x,t)u_{0}(x)dx=\int _{D}\Psi (x^{*}-x,t)u_{0}(x)dx=\int _{0}^{2}\int _{0}^{2}\Psi (x^{*}-x,y^{*}-y,t)u_{0}(x,y)dxdy$$

In $\mathbb {R} ^{2}$ hat die Fundametallösung nun folgende Form:

$$u(x,t)=\Psi (x,t)={\frac {1}{4\pi at}}\exp \left(-{\frac {\|x\|^{2}}{4at}}\right)$$

Die Berechnung der Fundamentallösungsmatrizen 'psi' zu den verschiedenen Zeitpunkten erfolgt mittels einer Zeitschleife. Ebenso wie in der Zeitunabhängigen Diffusion werden zuerst die Werte der Fundamentalfunktion $\Psi$ für jeden Gitterpunkt $x(j,i),y(j,i)$ um ein festes $x^{*}\in D_{h}$ verschoben und in der Matrix 'psi' gespeichert.

Auch hier kann das doppelte Integral mit der Trapezregel berechnet werden. Damit nach der Zeitschleife auf die verschiedenen Lösungen zugegriffen werden kann, werden diese mit dem Befehl $Losung(:,:,k+1)=J$ gespeichert.

for k=0:T*Zeitschritte
   t=t0+k*dt
   for i=1:(length(X)) 
       for j=1:(length(Y))
          xstar=x(j,i)*ones(length(Y),length(X));
          ystar=y(j,i)*ones(length(Y),length(X));
          psi= (1/(4*pi*a*t))*(exp(-((xstar.-x).^2+(ystar.-y).^2))/(4*a*t)); 
          J(j,i) = trapz(Y,trapz(X,psi.*u0,2));
       endfor
   endfor
   Losung(:,:,k+1)=J;
endfor

Durch eine weitere Schleife können die Grahiken ausgegeben werden

for k=0:T*Zeitschritte
  figure(k+1)
  meshc(x,y,Losung(:,:,k+1))
  grid on
  title(['Losung der Differenzialgleichung in t=', num2str(t0+k*dt)])
  xlabel('x')
  ylabel('y')
  test=["Fig_", num2str(k+1),".jpg"]  %Speichern der Bilder
  saveas(k+1, test)
endfor

Veränderungen

3.Tutoriumsaufgabe: Kompartimentmodelle für die dynamische Beschreibung der Infektionsverbreitung und die Datenlage [9]

In dieser Tutoriumsaufgabe soll die Verbreitung des Corona-Virus mithilfe der sogenannten Kompartimentmodelle beschrieben werden. Diese gehören zum logistischen Wachstumsmodell, welches ein Populationswachstum beschreiben, dass eine Verlangsamung erfährt, wenn es weniger Kapazität im System gibt. Bezogen auf den Corona-Virus meint die freie Kapazität die Gesamtbevölkerung $B$ abzüglich aller Infizierten, Immunen, und Verstorbenen $I(t)$. Die Ausbreitung des Virus wird also langsamer, wenn nicht mehr so viele noch nicht infizierte Individuen übrig sind, um sich anzustecken. Auf diesem Prinzip beruht auch die Herdenimmunität.

Mathematisch besagt das logistische Wachstumsmodell, dass Anstieg der Infizierungen in neuen Zeitpunkt $t+\Delta t$, proportional zum Bestand $I(t)$ und der freien Kapazität $(B-I(t))$ ist. Dabei ist $k$ die logistische Wachstumsrate bzw. Infektionsrate. Damit gilt:

$I(t+\Delta t)-I(t)=\Delta t.k.I(t)(B-I(t)).$

Über die Division von $\Delta t$ und den Grenzübergang $\Delta t\to 0$ erhält man die Differenzialgleichung

$I'(t)=kI(t)(B-I(t)),\ I(t_{0})=I_{0}$

mit der Lösung:

$I(t)={\frac {BI_{0}}{I_{0}+(B-I_{0})e^{-kB(t-t_{0})}}}.$

Bei den Kompartimentmodellen werden nun unterschiedliche Populationgruppen und deren Wechselwirkungen betrachtet. Zunächst betrachten wir das vereinfachte SI-Modell, anschließend das SIR- und zuletzt das modifizierte SIR-Modell.

SI Modell

Im SI Modell steht $S$ für susceptible (Empfängliche) und $I$ für infected (Infizierte). In diesem Modell gelten folgende Gleichungen:

$S'(t)=-k*S(t)*I(t)$;

$I'(t)=k*S(t)*I(t)$;

$S(t_{0})=B-I_{0}$;

$I(t_{0})=I_{0}$;

Dabei ist $k$ die Infektionsrate und $B$ die Gesamtbevölkerung.

Es soll angenommen werden, dass die Kapazität der deutschen Bevölkerung (83 Mio.), die sich infizieren wird 2 Drittel beträgt, also 55.000.000.

Es gilt hier das Erhaltungsgesetz $S'(t)+I'(t)=0$, das beschreibt, dass die Gesamtpopulation $S(t)+I(t)=B$ konstant erhalten bleibt.

Definition der Parameter

B= 55000 %Kapazität (in Tausend)
k= 0.32450 %Infektionsrate
times=(0:0.1:180); %Zeitspanne
I0= 16/1000 %Anzahl der Infizierten in T0

%Anfangswerte als Spaltenvektor
yo=[B-I0; I0;]

Funktion der rechten Seite einbauen

Definiere die Funktion f der rechten Seite des DGL-Systems $y'=f(y,t)$

% Vektorwertige Funktion f
f=@(y,x) [-k*y(1)*y(2)/B;k*y(1)*y(2)/B;]

%numerische Lösung
y = lsode (f, yo, times);

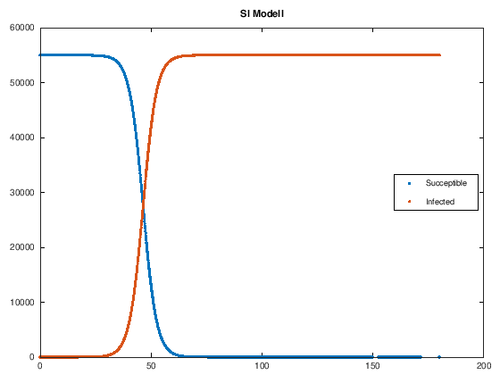
Graphische Darstellung SI Modell

Betrachtung verschiedener Infektionsraten

Wir betrachten hier verschiedene allgemeine Infektionsraten, erst einmal unabhängig von der Corona-Verbreitung.

k0= 0.1;
k1= 0.2;
k2= 0.5;
k3= 0.8;
k4= 0.99;

Es werden nun für jede Infektionsrate die jeweilige Funktion der rechten Seite gebildet:

% Vektorwertige Funktion f
t=@(y,x) [-k0*y(1)*y(2)/B;k0*y(1)*y(2)/B];
g=@(y,x) [-k1*y(1)*y(2)/B;k1*y(1)*y(2)/B];
h=@(y,x) [-k2*y(1)*y(2)/B;k2*y(1)*y(2)/B];
m=@(y,x) [-k3*y(1)*y(2)/B;k3*y(1)*y(2)/B];
n=@(y,x) [-k4*y(1)*y(2)/B;k4*y(1)*y(2)/B];

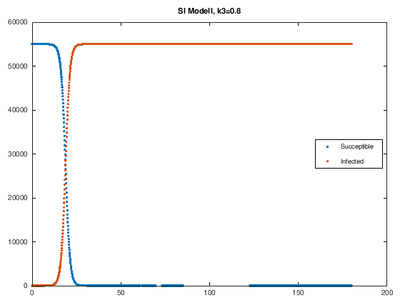
Ergebnis

Die gewählten Infektionsraten zeigen große Unterschiede in Bezug auf die Ausbreitungsgeschwindigkeit. Je größer die Infektionsrate desto schneller findet die Infizierung statt. Bei einer Infektionsrate k>0.4 sind die Verläufe allerdings in Bezug auf die aktuelle Corona-Verbreitung unrealistisch (siehe Datenvergleich), da die tatsächliche Übertragung von Corona langsamer verläuft.

SIR Modell

Das SIR Modell betrachtet im Vergleich zum SI Modell eine neue Gruppe der genesenen Individuen, die nach der Genesung die Gruppe der Infizierten verlassen und in die Gruppe der Genesenen oder Toten (R) mit einer bestimmten Rate $w$ wechseln.
Im SIR Modell steht S für susceptible (Empfängliche), I für infected (Infizierte) und R für removed (Genesene). In diesem Modell gelten folgende Gleichungen:

$S'(t)=-k*S(t)*I(t)$

$I'(t)=k*S(t)*I(t)-w*I(t)$

$R'(t)=w*I(t)$

Dabei ist $k$ die Infektionsrate, $B$ die Gesamtbevölkerung und $w={\frac {1}{T}}$ der Umkehrwert der Genesungszeit $T$.

Es soll angenommen werden, dass die Kapazität der deutschen Bevölkerung 2 Drittel beträgt. Damit gilt für B (in Tausend):

$S(t_{0})=B=55.000$

Es gilt hier das Erhaltungsgesetz $(S(t)+I(t)+R(t))'=0$, das beschreibt, dass die Gesamtpopulation $S(t)+I(t)+R(t)=B$ konstant erhalten bleibt.

Definition der Parameter

B= 55000 %Kapazität (in Tausend)
k= 0.32450 %Infektionsrate
w=1/14 % Wechselrate zu den Genesenen
times=(0:0.1:180);%Zeitspanne
I0= 16/1000 %Anzahl der Infizierten in T0
R0= 0 %Anzahl der Genesenen in T0

%Anfangswerte als Spaltenvektor
yo=[B-I0; I0; R0]

Funktion der rechten Seite einbauen

% Vektorwertige Funktion f
f=@(y,x) [-k*y(1)*y(2)/B;k*y(1)*y(2)/B-w*y(2);w*y(2)];

%numerische Lösung
y = lsode (f, yo, times);

Graphische Darstellung

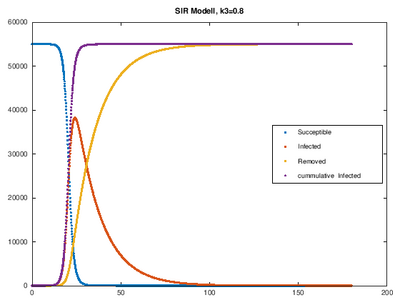
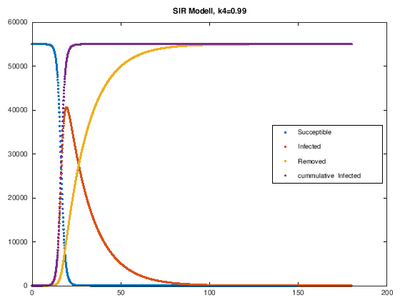
Betrachtung verschiedener Infektionsraten

Wir betrachten hier verschiedene Infektionsraten für allgemeine Verbreitungen. Die Raten k>0.4 sind für die Corona-Verbreitung unrealistisch, aber zeigen interessante Verhalten der Kurven.

k0= 0.1;
k1= 0.2;
k2= 0.5;
k3= 0.8;
k4= 0.99;

% Vektorwertige Funktion f
t=@(y,x) [-k0*y(1)*y(2)/B;k0*y(1)*y(2)/B-w*y(2);w*y(2)];
g=@(y,x) [-k1*y(1)*y(2)/B;k1*y(1)*y(2)/B-w*y(2);w*y(2)];
h=@(y,x) [-k2*y(1)*y(2)/B;k2*y(1)*y(2)/B-w*y(2);w*y(2)];
m=@(y,x) [-k3*y(1)*y(2)/B;k3*y(1)*y(2)/B-w*y(2);w*y(2)];
n=@(y,x) [-k4*y(1)*y(2)/B;k4*y(1)*y(2)/B-w*y(2);w*y(2)];

Im Graphen für k0=0.1 kann der Verlauf nicht erfasst werden, da dieser außerhalb des betrachteten Zeitraums liegt. Daher soll im folgenden eine größere Zeitspanne betrachtet werden.

Ergebnis

Auch hier kann man erkennen, dass die Infektionsraten für k>0.4 unrealistisch für die Corona-Verbreitung ist. Bei k=0.99 wäre die Infektion bereits im März überstanden. Das macht, bezogen auf Corona, keinen Sinn.

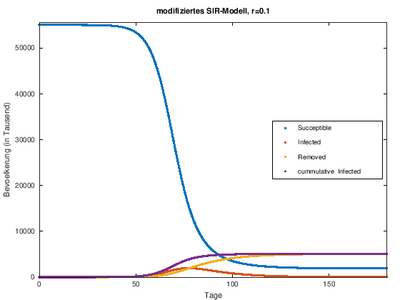
Modifiziertes SIR Modell

Das modifizierte SIR Modell soll eine Anpassung des ursprünglichen SIR Modells darstellen. Es ist vor allem relevant bei der Betrachtung der aktuellen Daten, also der gemeldeten Infizierten-Zahlen. Bei $r=0.1$ wurde die Annahme getroffen, dass lediglich 10% der Infizierten gemeldet wurden. Die tatsächlich Infizierten zeigen zum Beispiel keine Symptome und wurden daher nicht als krank erfasst. In diesem Modell gelten folgende Gleichungen:

$S'(t)=-{\frac {c(t)}{rB}}*S(t)*I(t)$

$I'(t)={\frac {c(t)}{B}}*S(t)*I(t)-w*I(t)$

$R'(t)=w*I(t)-d*I(t)$

$S(t_{0})=B-I_{0}$

$I(t_{0})=I_{0}$

$R(t_{0})=0$

Zu den Parametern:

• $B=55.000$ ist die Kapazitätsgrenze (Bevölkerung, die sich insgesamt ansteckt)
• $c,k$ verschiedene Infektionsraten,
• $d=0.003$ ist die konstante Sterberate, mit der die Infizierten aus der Gesamtpopulation ausscheiden,
• $R$ beschreibt die Population der Genesenen (ohne Tote),
• $r$ ist ein konstanter Faktor, der den prozentualen Anteil, der durch Tests erfassten Infizierten (Erkrankten) beschreibt
• $w={\frac {1}{14}}$ ist die tägliche Wechselrate der Infizierten in die Gruppe der Genesenen (oder Toten), 14 Tage Genesungszeit

Es gilt hier das Erhaltungsgesetz $S'+{\frac {I'}{r}}+{\frac {R'}{r}}=-dI$, das besagt, dass sich die Gesamtpopulation $S+{\frac {I}{r}}+{\frac {R}{r}}$ um die verstorbenen Infizierten verringert. Falls $d=0$ werden die Toten in der Gruppe R der Genesenen mitgezählt und es folgt $S+{\frac {I}{r}}+{\frac {R}{r}}=N$. Gilt zusätzlich $r=1$ erhalten wir das original SIR Modell.

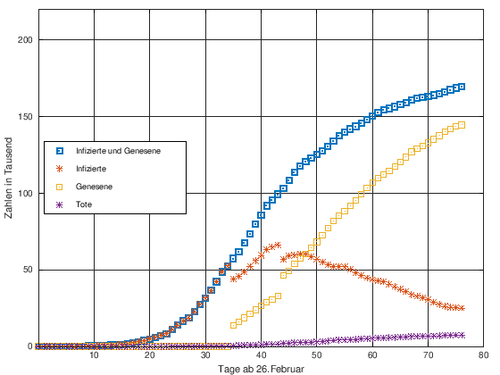
Aktuelle Daten

Um die aktuellen Daten der Corona-Verbreitung darzustellen, wird eine vorgegebene coronaData-Datei verwendet, welche die vom RKI ermittelten täglichen Daten der Corona-Infizierten in Deutschland seit dem 26. Februar 2020 enthält. Wir erhalten so eine Rückgabe-Matrix, die uns in der ersten Zeile die kumulierten Infizierten, in der zweiten Zeile die Todesfälle und in der dritten Zeile die Genesenen speichert.

A=coronaData();
Infizierte=A(1,:);
Tote=A(2,:);
Genesene=A(3,:);

Die aktuell Infizierten ergeben sich aus der Differenz aller Infizierten und der Genesenen:

Infizierte_aktuell=Infizierte-Genesene;
n=length(Infizierte);
times=[0:1:n-1];

Graphische Darstellung

Bestimmung einer geeigneten Infektionsrate

Es soll nun eine geeignete Infektionsrate c bestimmt werden, die das exponentielle Wachstum (bis ca. Ende April 2020) einigermaßen gut abbildet. Hierfür wird folgende exponentielle Funktion $I(t)=I_{0}e^{k*(t-t_{0})}$ mit den Daten des RKIs bzgl. der Infizierten in Deutschland verglichen.

Wir betrachten für die folgende Funktion die ersten 30 Tage, da dieser Teil der Glockenkurve am ehesten einer exponentiellen Funktion gleicht. Werden deutlich mehr Tage betrachtet, kann die Exponentialfunktion nicht mehr als Annäherung dienen:

t_0=0;
I_0=16;
k=0.254; %Bestimmung siehe unten
t=[1:1:30];
$I(t)=I_{0}e^{k*(t-t_{0})}$

In der folgenden Abbildung sind die Graphen der gewählten Exponentialfunktion (orange) und der RKI Daten (blau) dargestellt.

Bestimmung des Residuums

Im folgenden soll das Residuum bestimmt werden. Dies gilt als Abweichung von einem gewünschten Ergebnis. Es gilt: Je kleiner das Residuum ist, desto näher liegt die Näherung bei der Lösung. Das Residuum kann somit als Maß der Abweichung der Näherung von der exakten Lösung betrachtet werden (siehe Residuum).

Zunächst wird die Abweichung für jeden Punkt bestimmt. Die Summe gibt den gesamten Fehler in Form des Residuums an.

for i=1:30    %Berechnung für jeden der 30 Tage
   Infizierte=A(1,i);
   I(i)=I_0*exp(k*(i-t_0));
   S(i)=(Infizierte.-I(i)).^2;
endfor
j=[1:30];
S(j)
Summe=sum(S(j))    %Gesamtabweichung aller Tage

Anpassung von c

Das Residuum kann für verschiedene Infektionsraten bestimmt werden. Dafür wird die Infektionsrate zwischen 0.2 und 0.3 in 0.002er Schritten verwendet. Durch Augenmaß konnten kleinere und größere Infektionsraten ausgeschlossen werden.

Summe=0;
for k=[0.2:0.002:0.3]
   for i=1:30
       Infizierte=A(1,i);
       I(i)=I_0*exp(k*(i-t_0));
       S(i)=sum((Infizierte.-I(i)).^2);
   endfor
   j=[1:30];
   S(j);
   Summe=[Summe , sum(S(j))];
endfor

Davon wird das minimale Residuum bestimmt. Außerdem sollen die verschiedenen Residuen graphisch gegenübergestellt werden.

MIN=min (Summe(2:length(Summe)));
index=find(Summe==MIN); 
k=[0.2:0.002:0.3];
optim_Infrate=k(index)

Ergebnis

Nachdem wir nun das Minimum der Residuen bestimmt haben und den zugehörigen Graphen analysiert haben, folgt, dass damit die geeignete Basisinfektionsrate bei $k=0.254$ liegt.

Einbauen einer Slowdown-Funktion

Im folgenden Schritt sollen zwei verschiedene Slowdown-Funktionen zur Verlangsamung der Infektionsrate eingebaut und miteinander verglichen werden. Es soll überprüft werden, welche der beiden Funktionen besser in Einklang mit den Kontakt- und Lockerungsmaßnahmen stehen.

Folgende Kontakt- und Lockerungsmaßnahmen spielen dabei eine Rolle:

* Schulschließung am 15.März (Tag 19)
* Kontaktverbot am 22.März (Tag 26)
* Lockerung der Maßnahmen ab 27.April (Tag 61)

Slowdown-Funktion-1

Ab Tag t (Argument der Funktion) wird die Infektionsrate in mehreren Schritten sinken.

function val=slowdown(x,t)
if x<t val=1 ;   else if x<t +10 val=t./(x.^1.05); else if x<t +22 val=t./(x.^1.2); else val=t./(x.^1.27)  ;
endif
endif
endif
if x> 80  val=0.5; endif
endfunction

Die beispielhafte Lockerung der Maßnahmen gilt ab Tag 80, welche die Infektionsrate wieder auf 50% der Basisinfektionsrate erhöht. So kann der Effekt der Lockerung zu beispielhaft beobachtbar gemacht werden.

Slowdown-Funktion-2

function val=slowdown2(x,t)
if x<t val=1 ; else if x<t +8 val=t./(x.^1.1); else if x<t +16 val=t./(x.^1.25); else if x<t +22 val=t./(x.^1.4); 
else  val=t./(x.^1.5)
endif
endif
endif
endif
if x> 80  val=0.5; endif
endfunction

Vergleich RKI Daten mit Slowdown-Funktion

Im folgenden wird die Infektionsrate aus den RKI- Daten berechnet: $c_{Data}(t)={\frac {I_{RKI}(t)-I_{RKI}(t-1)}{I_{RKI}(t-1)}}$, wobei $I_{RKI}(t)$ die kumulative Anzahl der Infizierten (RKI-Data) bezeichnet, t- Zeit in Tagen.

A=coronaData();
 Infizierte=A(1,:);
 Genesene=A(3,:);
 Tote=A(2,:);

Infizierte_aktuell=Infizierte-Genesene;

n=length(Infizierte);
 times=[0:1:n-1];

c=0.3245;
k=0.254;

for i=1:length(times)
cc(i)=slowdown (times (i), 25)*c;
hh(i)=slowdown2(times (i), 25)*c;
kk(i)=slowdown2 (times (i), 25)*k;
endfor 

Berechnung der Infektionsrate aus den RKI-Daten:

T=1;
ccc(1)=cc(1);
for i=T+1:n
ccc(i-T)=(Infizierte(i)-Infizierte(i-T))/(Infizierte(i-T) );
endfor

Ergebnis In der obigen Abbildung kann man erkennen, dass die 2. Slowdown-Funktion mit der zuvor angepassten Infektionsrate von 0.254 am besten zu den tatsächlichen Daten des RKI passt.

Relativer Fehler

Um das vorherige Ergebnis zu verifizieren, wird im folgenden Abschnitt der relative Fehler der Infizierten berechnet.

B=55000;
I0=16/1000;
R0=0;
r=0.1;
w=1/14;
t=(0:0.1:180);
yo=[B-I0; I0; R0];

f=@(y,x) [-c*slowdown(x,25)*y(1)*y(2)/(r*B);c*slowdown(x,25)*y(1)*y(2)/B-w*y(2);w*y(2)-0*y(2)];
g=@(y,x) [-c*slowdown2(x,25)*y(1)*y(2)/(r*B);c*slowdown2(x,25)*y(1)*y(2)/B-w*y(2);w*y(2)-0*y(2)];
h=@(y,x) [-k*slowdown2(x,25)*y(1)*y(2)/(r*B);k*slowdown2(x,25)*y(1)*y(2)/B-w*y(2);w*y(2)-0*y(2)];
y1= lsode (f, yo, t);
y2= lsode (g, yo, t);
y3= lsode (h, yo, t);

%Interpolation der Funktionswerte an die RKI-Zeiten (Tage)
I1=interp1 (t, y1(:,2), times);
I2=interp1 (t, y2(:,2), times);
I3=interp1 (t, y3(:,2), times);

%Relativer Fehler: Slowdown 2 und k=0.254
rel_I3=abs(I3-Infizierte_aktuell./1000)./(Infizierte_aktuell./1000);

%Relativer Fehler: Slowdown 2 und k=0.3245
rel_I2=abs(I2-Infizierte_aktuell./1000)./(Infizierte_aktuell./1000);

%Relativer Fehler: Slowdown 1 und k=0.3245
rel_I1=abs(I1-Infizierte_aktuell./1000)./(Infizierte_aktuell./1000);

plot (times,rel_I1,'y',times,rel_I2,'g',times,rel_I3,'b')
title ('Relativer Fehler I')
legend('I1','I2','I3')

Ergebnis: Grundsätzlich sind in den ersten 40 Tagen alle drei Fehler relativ gleich, wobei die ursprüngliche Slowdownfunktion mit c=0.3245 am günstigsten ist. Für die zukünftige Betrachtung hat dann aber die andere Slowdownfunktion einen deutlich geringeren Fehler.

Modifiziertes SIR-Modell und aktuelle Daten

Im folgenden Abschnitt wird die Slowdown-Funktion2 in das modifizierte SIR-Modell eingebaut und zusammen mit den aktuellen Daten implementiert:

function val=slowdown2(x,t)
if x<t val=1 ; else if x<t +8 val=t./(x.^1.1); else if x<t +16 val=t./(x.^1.25); else if x<t +22 val=t./(x.^1.4); 
else  val=t./(x.^1.5)
endif
endif
endif
endif
if x> 80  val=0.5; endif
endfunction

Implementierung des modifizierten SIR-Modells

Die optimale Infektionsrate c=0.254, die wir in den vorherigen Schritten bestimmt haben, passt zwar sehr gut zur berechneten Infektionsrate der RKI-Daten, aber nicht mehr zu unserer Verbreitung innerhalb des modifizierten SIR-Modells und dem Slowdown-Geschehen. Deshalb wurde diese Infektionsrate im folgenden Modell auf c=0.35 erhöht und angepasst. Würde hier die Infektionsrate c=0.254 verwendet werden, ergibt sich ein deutlich größerer relativer Fehler bis zu 95%.

B=55000; %Kapazitätsgrenze, 2/3 der deutschen Bevölkerung
c=0.35; %Basisinfektionsrate- die Rate des exponentiellen Wachstums am Anfang der Pandemie
w=1/14; %Wechselrate zu den Genesenen
d=0.003; %Todesrate
r=0.1; %Anteil der erfassten Infizierten
I0=16/1000; %Anzahl der Infizierten in T0
R0=0; %Anzahl der Genesenen in T0

times=(0:0.1:180);

%Anfangswerte
yo=[B-I0;I0;R0];

%Funktion f der rechten Seite des DGL-Systems y'=f(y,t)
f=@(y,x) [-c*slowdown2(x, 25)*y(1)*y(2)/(r*B);c*slowdown2(x, 25)*y(1)*y(2)/B-w*y(2);w*y(2)-d*y(2)];
y = lsode (f, yo, times);

Einfluss der Lockerung der Maßnahmen

Nun soll anhand des SIR Modells untersucht werden, welchen Einfluss ein Anstieg der Infektionsrate in Folge der Lockerung der Kontaktverbot-Maßnahmen auf die Anzahl der Infizierten hat. Die Lockerung der Maßnahmen erfolgte am 27. April, also am Tag 61, die die Infektionsrate wieder auf 50% der Basisinfektionsrate erhöht.

Hierfür erstellen wir eine dritte Slowdown-Funktion, welche zum oben genannten Geschehen passt:

function val=slowdown3(x,t)
if x<t val=1 ; else if x<t +8 val=t./(x.^1.1); else if x<t +16 val=t./(x.^1.25); else if x<t +22 val=t./(x.^1.4); 
else val=t./(x.^1.5);
endif
endif
endif
endif
if x> 61  val=0.5 ; endif
endfunction

n=length(Infizierte);
 times=[0:1:n-1];

k=0.35;

for i=1:length(times)
kk(i)=slowdown3 (times (i), 25)*k;
endfor

Einfluss von r

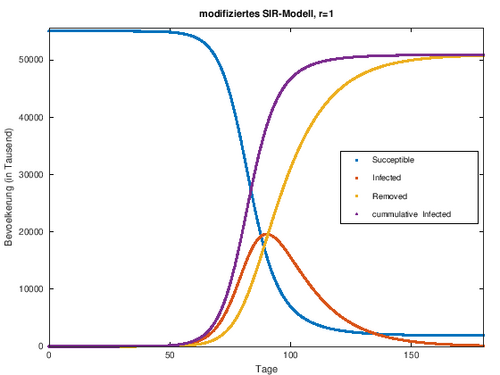
Zum Schluss soll ein Szenario der Pandemie in Deutschland dargestellt werden, welches möglicherweise ohne die kontaktreduzierenden Maßnahmen, also ohne Slowdown-Funktion auftreten könnte. Es wird untersucht, welchen Einfluss der Parameter r (Anteil der tatsächlich Infizierten) in dieser Modellierung hat. Dazu wird das modifizierte SIR-Modell implementiert. Zunächst erhalten wir für r=1 das original SIR-Modell:

Parameter

B=55000; 
c=0.250; 
w=1/14; 
d=0.003; 
r=1;
I0=16/1000; %Anzahl der Infizierten in T0
R0=0; %Anzahl der Genesenen in T0

times=(0:0.1:180);
%Anfangswerte
yo=[B-I0;I0;R0];

%Funktion f der rechten Seite des DGL-Systems y'=f(y,t)  
f=@(y,x) [-c*y(1)*y(2)/(r*B);c*y(1)*y(2)/B-w*y(2);w*y(2)-d*y(2)];
y = lsode (f, yo, times);

Danach betrachten wir verschiedene Werte r<1:

r1=0.8;
r2=0.5;
r3=0.3;
r4=0.1;

Ergebnis Je größer man r wählt, desto mehr der tatsächlich Infizierten können erfasst werden. Je kleiner man r wählt, desto flacher werden die Graphen. Für r=1 erhalten wir dann unser SIR-Modell (Ausgangsmodell). Würde man r>1 festlegen, dann würden mehr Infizierte erfasst werden als tatsächlich vorliegen.

4.Tutoriumsaufgabe: Randwertaufgabe für Poissongleichung mit Finite-Differenzen-Verfahren [10]

In diesem Skript wird stationäre Diffusion mithilfe der Poissongleichung auf einem recheckigem Gebiet mithilfe der Finiten Differenzen Methode implementiert. Diese Methode ist dabei ein Gitter-basiertes Verfahren, welches die unbekannte Funktion $u(x,t)$ auf endlich vielen Gitterpunkten $P_{i,j}=(x_{i},y_{j}),\ i=1,\ldots N_{x},\ j=1,\ldots N_{y}$ approximiert.

$$-a\Delta u=f~in~D=(0,X_{end})x(0,Y_{end}),$$

$$u(x)=g(x)~auf~\partial D$$

Quelldichtefunktion f der rechten Seite der Poissongleichung

Als Quelldichtefunktion beschreibt $f$ die Flussgeschwindigkeit in das System hinein, also die Neuinfizierungen die kontinuierlich hinzukommen.

function wert=Quellfunktion(x,y)
 if sqrt((x.-5).^2+(y.-3).^2)<=0.35 wert=1;
   else wert=0;
 endif
endfunction

Gebiet D

Um das Gebiet festzulegen, müssen zunächst die Kantenlängen des Rechtecks festgelegt werden. Außerdem wird die Anzahl an Gitterpunkten in X-Richtung festgelegt.

xend=8; 
yend=5;
N=30       %Anzahl von X-Punkten (ohne Randpunkten)

Um das äquidistane Gitter zu erstellen, muss der Abstand zwischen den einzelnen Gitterpunkten bestimmt werden. Dafür muss die x-Kantenlänge durch $N+1$ geteilt werden. Dies liegt daran, dass der 0-te, und (N+1)-te, Index den Rändern entsprechen und somit nicht zu den Gitterpunkten zählen.

hx=xend/(N+1)
hy=hx;
M=floor((yend/hy))-1
%Koordinatenmatrix der Gitterpunkte
[x,y]=meshgrid(hx:hx:xend-hx,hy:hy:yend-hy);

a=1.0; %konstanter Diffusionskoeffizient (beschreibt die Verbreitungsgeschwindigkeit; je größer, desto schneller)

Randbedingungen

Bei einem Dirichlet Randwertproblem wird die gesuchte Funktion $u$ am Rand $\partial D$ durch eine Funktion $g$ festgelegt.

$-\Delta u(x)=f(x)~~~~{\mbox{in}}~~D\subset \mathbb {R} ^{2},$

$u(x)=g(x)~~~~~~~~~~{\mbox{auf}}~~\partial D$

In unserem Fall soll die Funktion $g$ für die verschiedenen Ränder einen konstanten Wert annehmen.

%Dirichlet RB:
wert_unten=-0.025;                                  
wert_oben=0.025;
wert_links=0.025;
wert_rechts=-0.025;

Systemmatrix

Theorie

Um die gesuchte Funktion $u$ zu berechnen, muss eine Approximation für $\Delta u(x)$ gefunden werden.

Eindimensional kann dabei $u''$ betrachtet werden. Die zweite Ableitung kann dabei mit Hilfe des zentralen Differenzenquotienten diskretisiert werden:

$D_{h}^{2}u(x_{i})={\frac {u_{i+1}-2u_{i}+u_{i-1}}{h^{2}}}\approx u''(x_{i})$ für jedes $i=1,\ldots n$.

Hier bezeichnet $u_{i}:=u(x_{i})$.

Dieser ergibt sich aus der Differenz der ersten Differenzenquotienten $D_{h}^{+}u(x_{i})-D_{h}^{-}u(x_{i})$, wobei der Rückwärtsdifferenzenquotient vom Vorwärtsdifferenzenquotient abgezogen wird.

Unsere Betrachtung soll jedoch zweidimensional sein, da wir ein rechteckiges Gebiet $D$ betrachten. Daher müssen zwei Raumrichtungen x und y berücksichtigt werden und somit auch zwei Differenzenquotienten $D_{h,x}^{2}u(x_{i},y_{j}),\ D_{h,y}^{2}u(x_{i},y_{j})$ aufgestellt werden.

Diese werden durch die folgenden partiellen Ableitungen im Punkt $(x_{i},y_{j})$ approximiert:

${\frac {\partial ^{2}u(x_{i},y_{j})}{\partial x^{2}}}\approx D_{h,x}^{2}u(x_{i},y_{j}):={\frac {u(x_{i+1},y_{j})-2u(x_{i},y_{j})+u(x_{i-1},y_{j})}{h^{2}}}={\frac {u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{h^{2}}}$,

${\frac {\partial ^{2}u(x_{i},y_{j})}{\partial y^{2}}}\approx D_{h,y}^{2}u(x_{i},y_{j}):={\frac {u(x_{i},y_{j+1})-2u(x_{i},y_{j})+u(x_{i},y_{j-1})}{h^{2}}}={\frac {u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{h^{2}}}$

Damit ergibt sich:

$$\Delta u(x_{i},y_{j})\approx {\frac {u_{i+1,j}+u_{i,j+1}-4u_{i,j}+u_{i-1,j}+u_{i,j-1}}{h^{2}}},\qquad i=1,\ldots n,\ j=1,\ldots m.$$

Um nun eine Systemmatrix aufzustellen zu können, müssen zunächst unsere unbekannten Funktionswerte $u(x_{i},y_{j})$ aller Gitterpunkte, sowie die Funktionswerte der rechten Seite $f(x_{i},y_{j})$ in je einen langen Vektor eingeordnet werden. Diese sollen folgendermaßen (in der selben Reihenfolge) aufgestellt werden:

${\vec {u}}_{h}=(u_{1,1},u_{2,1},\ldots u_{n,1}|\ldots |u_{1,m},\ldots u_{n,m})^{T}$

${\vec {f}}_{h}=(f_{1,1},f_{2,1},\ldots f_{n,1}|\ldots |f_{1,m},\ldots f_{n,m})^{T}$

Damit kann nun ein lineares Gleichungssystem $A_{h}{\vec {u}}_{h}={\vec {f}}_{h}$ aufgestellt werden, wobei $A_{h}\in {\mathbb {R} }^{n.m\times n.m}$unsere blockdiagonale Matrix ist. Dabei gilt:

$A_{h}={\frac {-1}{h^{2}}}{\begin{pmatrix}B&I&&\ldots &0\\I&B&I&&\vdots \\\vdots &\ddots &\ddots &\ddots &\\&&I&B&I\\0&\ldots &0&I&B\end{pmatrix}}$ mit Diagonalblock $B={\begin{pmatrix}-4&1&0&\ldots &0\\1&-4&1&\ldots &0\\\vdots &\ddots &\ddots &\ddots \\&&1&-4&1\\0&\ldots &0&1&-4\end{pmatrix}},\quad B\in {\mathbb {R} }^{n\times n}$

und der Einheitsmatrix $I=E_{n}\in {\mathbb {R} }^{n\times n}$ auf der Nebendiagonale.

Implementierung

Diese Systemmatrix soll nun aufgestellt werden.

 Vec1=ones(N*M,1); % erzeugt Vektor der  Länge N*M
 BB=diag(-4.*Vec1,0)+diag(ones(N*M-1,1),1)+ diag(ones(N*M-1,1),-1)+diag(ones(N*(M-1),1),N)+diag(ones(N*(M-1),1),-N);
%Systemmatrix N^2xM^2 mit -4 auf der Diagonale und 1 auf den Nebendiagonalen und 1 auf N und -N-ter Nebendiagonale 

Nun muss jedoch noch berücksichtigt werden, dass beim Übergang in die nächste Blockmatrix B die Nebendiagonalen aus Einsen unterbrochen werden und je ein Nulleintrag vorliegt.

${\begin{pmatrix}-4&1&0~&1&0&0\\1&-4&1~&0&1&0\\0&1&-4~&0&0&1\\\\1&0&0~&-4&1&0\\0&1&0~&1&-4&1\\0&0&1~&0&1&-4\end{pmatrix}}$

Dies muss also noch korrigiert werden.

 %Korrektur der Matrix (Blockdiagonalität)
 for  i=1:(M-1) 
     BB(i*N+1,i*N)=0;BB(i*N,i*N+1)=0;
 endfor
 
%Matrix mit Diffkoeffizient a/h^2 multiplizieren 
 BB=BB*a/hx^2;
  
%Matrixdarstellung
figure (1);
spy (BB);
xlabel("Spalten")
ylabel("Zeilen")
zlabel("Matrix B")
title ("Systematrix B");

rechte Seite des Systems

Um die rechte Seite des Sytems aufzustellen, wird zunächst die Quellfunktion für jeden Gitterpunkt eingespeichert. Anschließend werden die Dirichlet Randbedingungen hinzugefügt.

clear f;
 for  i=1:N
 for j=1:M
   f(j,i)=1*Quellfunktion(x(j,i),y(j,i));
    %Dirichlet Randbedingung unten und oben:
    if j==1 f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+wert_unten*a/hx^2; endif
    if j==M f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+wert_oben*a/hx^2; endif
    %Dirichlet Randbedingung links und rechts:
    if i==1 f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+ wert_links*a/hx^2; endif
    if i==N f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+ wert_rechts*a/hx^2; endif        
  endfor
  endfor

Ecken-Beiträge

Die Eckbeiträge müssen gesondert betrachtet werden, da hier zwei Randbedingungen eingehen.

f(1,1)=1*Quellfunktion(x(j,i),y(j,i))+(wert_links+wert_unten)*a/hx^2;
f(1,N)=1*Quellfunktion(x(j,i),y(j,i))+(wert_rechts+wert_unten)*a/hx^2;
f(M,1)=1*Quellfunktion(x(j,i),y(j,i))+(wert_links+wert_oben)*a/hx^2;
f(M,N)=1*Quellfunktion(x(j,i),y(j,i))+(wert_rechts+wert_oben)*a/hx^2;

Schließlich kann die rechte Seite in den Vektor $b$ umgeformt werden. Außerdem fließt hier das $-1$ aus der Poisson-Gleichung $-\Delta u(x)=f(x)$ ein.

 b=-1*reshape(f',N*M,1); %Muss transporniert werden, damit die Zeilen untereinander aufgestellt werden

%Lösungsschritt
 sol=BB\b;

 sol_matrix=reshape(sol,N,M);% Matrix mit N(Zeilen)x M(Spalten)
 sol_matrix=sol_matrix'; % Rücktransponierung nach reshape

Graphische Darstellung

 figure(2);
 surfc(x,y,sol_matrix);
 title ("Loesung");
 ylabel("y")
 xlabel("x")
 
 figure(3);
 surfc(x,y,f);
 title ("Quellfunktion");
 ylabel("y")
 xlabel("x")

Erweiterung des Modells mit Neumann-Randbedingungen

Im folgenden sollen die Dirichlet-Randbedingung mit den Neumann-Randbedingungen verknüpft werden. Dabei müssen die Richtungsableitungen der Funktion $u$ in der Richtung des äußeren Normalenvektors gegeben sein, wodurch $u$ die Neumann-Randbedingung erfüllt:

$-\Delta u(x)=f(x)\quad x\in D$

${\frac {\partial u(x)}{\partial {\vec {n}}}}\equiv \nabla u\cdot {\vec {n}}=g(x)\quad x\in \partial D.$

Da wir ein rechteckiges Gebiet gewählt haben, gilt insbesondere ${\frac {\partial u}{\partial {\vec {n}}}}=\pm {\frac {\partial u}{\partial x}}$ oder $\pm {\frac {\partial u}{\partial y}}$

• linker Rand: ${\frac {\partial u}{\partial x}}(x_{0},y_{j})=-\alpha ,\$
• rechter Rand: ${\frac {\partial u}{\partial x}}(x_{n+1},y_{j})=\beta ,\ j=1,\ldots m,$
• unterer Rand: ${\frac {\partial u}{\partial y}}(x_{i},y_{0})=-\gamma ,\$
• oberer Rand: ${\frac {\partial u}{\partial y}}(x_{i},y_{m+1})=\delta ,\ i=1,\ldots n,$

Im Folgenden wird allerdings die Finite-Differenzen-Methode (FDM) für Neumann-RB auf dem Rechteck D mit homogenen Randbedingungen mit $\alpha =\beta =\gamma =\delta =0$ implementiert.

Folglich muss unser betrachtetes Gitter um die Randwerte erweitert werden.

%Koordinatenfeld                     
 [x,y]=meshgrid(0:hx:xend,0:hy:yend);
 N=N+2;
 M=M+2;

Systemmatrix

Durch die Erweiterung des Gitters gibt es nun auch weitere unbekannte Funktionswerte $u(x_{i},y_{j})$. Der lange Vektor soll folgendermaßen aufgestellt werden:

${\vec {u}}_{h}=(u_{0,0},u_{1,0},\ldots u_{n,0},u_{n+1,0}|u_{0,1},u_{1,1},\ldots u_{n,1},u_{n+1,1}|\ldots |u_{0,m},u_{1,m},\ldots u_{n+1,m}|u_{0,m+1},u_{1,m+1},\ldots u_{n+1,m+1})^{T}$

Dabei sind die Punkte des ersten Spaltenabschnitts, die des unteren Gitterrandes. Die Punkte des letzten Spaltenabschnittes entsprechen den Gitterpunkten des oberen Randes. Zudem wurde jeder Spaltenabschnitt um einen neuen ersten und letzten Punkte erweitert. Dabei liegt der erste Punkt auf dem linken und der letzte Punkt auf dem rechten Rand.

Erweiterung: Neumann-Randbedungungen auf dem linken und rechten Rand

Die Dirichlet-Randbedingungen sollen nur an manchen Rändern durch Neumann-Randbedingungen ergänzt werden, jedoch nicht vollständig ersetzt, da sonst kein brauchbares Ergebnis herauskommt. Hier geschieht dies auf dem linken und rechten Rand. Das Gitter wird jedoch nicht darauf angepasst, wodurch ein kleiner Fehler entsteht.

Nun soll wieder das lineare Gleichungssystem $A_{h}{\vec {u}}_{h}={\vec {f}}_{h}$ aufgestellt werden. Dazu muss unsere blockdiagonale Matrix $A_{h}$ ebenfalls um Einträge erweitert werden, damit $A_{h}\in {\mathbb {R} }^{(n+2)(m+2)\times (n+2)(m+2)}$. Dabei wird der Diagonalblock $B$ jeweils um eine Zeile oben und unten erweitert. Diese ensprechen den Werten des linken und rechten Randes, weshalb hier ein anderer Eintrag erfolgen muss. Dieser leitet sich aus dem Differenzenquotienten her. So gilt beispielsweise für den linken Rand ${\frac {\partial u}{\partial x}}(x_{0},y_{j}))\approx D_{h,x}^{+}u(x_{0},y_{j})={\frac {u_{1,j}-u_{0,j}}{h}}={\frac {1}{h^{2}}}(hu_{1,j}-hu_{0,j})={\frac {-1}{h^{2}}}(hu_{0,j}-hu_{1,j})$, weshalb in der oberen Zeile $(h~-h~0\ldots 0)$ eingetragen werden muss.

Insgesamt sieht die Systemmatrix damit folgendermaßen aus:

$A_{h}={\frac {-1}{h^{2}}}{\begin{pmatrix}B&I^{*}&&\ldots &0\\I^{*}&B&I^{*}&&\vdots \\\vdots &\ddots &\ddots &\ddots &\\&&I^{*}&B&I^{*}\\0&\ldots &0&I^{*}&B\end{pmatrix}}$ mit Diagonalblock $B={\begin{pmatrix}h&-h&0&\ldots &0\\1&-4&1&\ldots &0\\\vdots &\ddots &\ddots &\ddots \\&&1&-4&1\\0&\ldots &0&-h&h\end{pmatrix}},\quad B\in {\mathbb {R} }^{n+2\times n+2}$ und null-erweiterter Einheitsmatrix $I^{*}={\begin{pmatrix}0&&&\ldots &0\\&1&&\ldots &\\\vdots &\ddots &\ddots &\ddots \\&&&1&\\0&\ldots &&&0\end{pmatrix}},\quad I^{*}\in {\mathbb {R} }^{n+2\times n+2}$.

Implementierung Zunächst wird die Systemmantrix genauso wie oben aufgestellt. Einziger Unterschied ist, dass hier gilt $N=N+2$ und $M=M+2$.

 Vec1=ones(N*M,1); % erzeugt vektor der  Länge N*M
 BB=diag(-4.*Vec1,0)+diag(ones(N*M-1,1),1)+ diag(ones(N*M-1,1),-1)+diag(ones(N*(M-1),1),N)+diag(ones(N*(M-1),1),-N);
 %Systemmatrix N^2xM^2 mit -4 auf der Diagonale und 1 auf den Nebendiagonalen und 1 auf den N und -N-ter Nebendiagonale 

%Korrektur der Matrix (Blockdiagonalität)
 for  i=1:(M-1) 
     BB(i*N+1,i*N)=0;BB(i*N,i*N+1)=0;
 endfor

% Matrix mit Diffkoeff/h^2 multiplizieren
 BB=BB*a/hx^2;

Neumann RB auf dem oberen und unteren Rand -einzelne Blöcke der Matrix ersetzen

Würde man auch Neumann-Randbedingungen auf dem oberen und unteren Rand implementieren wollen, so müsste man die Systemmatrix $A_{h}$ anpassen. Da dies in der Tutoriumsaufgabe 5 gebraucht wird, soll hier eine Auskommentierung vorbereitend stattfinden. Dabei werden oben und unten eine Blockzeile ergänzt, wobei einmal eine Diagonalmatrix aus $h$ und einmal aus $-h$ sowie Null-Matrizen ergänzt werden.

 h=hx;
 block=diag((a/h)*ones(N,1)); %a/h, denn a/h^2*h
 %unterer Rand
 %BB(1:N,1:N)=block;
 %BB(1:N,N+1:2*N)=-block;
 %oberer Rand
 %BB(N*(M-1)+1:N*M,N*(M-1)+1:N*M)=block;
 %BB(N*(M-1)+1:N*M,N*(M-2)+1:N*(M-1))=-block;

Neumann RB linker und rechter Rand - einzelne Zeilen der Matrix ersetzen

Wie oben beschrieben müssen die oberste und unterse Zeile der Blockmatrizen geändert werden. Dies geschieht in einer Schleife.

  for i=1:(M-2)
  vector_up=zeros(1,N*M);
  vector_up(N*i+1)=a/h;    %a/h eintragen, denn a/h = a/h^2*h (Matrix wurde schon mit a/h^2 multipliziert
  vector_up(N*i+2)=-a/h;
  vector_down=zeros(1,N*M);
  vector_down(N*i+N)=a/h;
  vector_down(N*i+N-1)=-a/h;
  BB(i*N+1,:)=vector_up ;   % Ersetzt entsprechende Zeile mit Vektor
  BB(i*N+N,:)=vector_down ;
 endfor

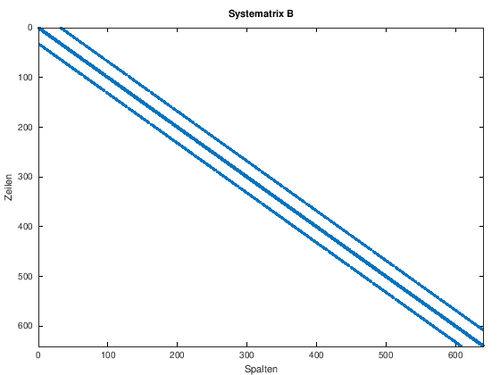
Matrixdarstellung

 figure (1);              
 spy (BB);
 xlabel("Spalten")
 ylabel("Zeilen")
 zlabel("Matrix B")
 title ("Systematrix B");

rechte Seite des Systems

 for i=1:N
 for j=1:M
  f(j,i)=1*Quellfunktion(x(j,i),y(j,i)); 
  %Neumann Randbedingung links und rechts:
  if i==1 f(j,i)=1*Quellfunktion(x(j,i),y(j,i)); endif
  if i==N f(j,i)=1*Quellfunktion(x(j,i),y(j,i)); endif
  %Dirichlet Randbedingung oben und unten:
  if j==1 f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+wert_unten*a/hx^2; endif
  if j==M f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+wert_oben*a/hx^2;  endif
  endfor
  endfor

Ecken-Beiträge

Da wir in unserem Fall in allen vier Ecken sowohl Neumann-RB als auch Dirichlet-RB haben, addieren sich keine zusätzlichen Eckbeiträge hinzu.

  f(1,1)=1*Quellfunktion(x(j,i),y(j,i));
  f(1,N)=1*Quellfunktion(x(j,i),y(j,i));
  f(M,1)=1*Quellfunktion(x(j,i),y(j,i));
  f(M,N)=1*Quellfunktion(x(j,i),y(j,i));

 b=-1*reshape(f',N*M,1); 

 % Lösungsschritt
 sol=BB\b;

 sol_matrix=reshape(sol,N,M); % Matrix mit N(Zeilen)x M(Spalten)
 sol_matrix=sol_matrix'; % Transponiert, wegen reshape

Graphische Darstellung

 figure(2);
 surfc(x,y,sol_matrix);
 title ("Loesung");
 ylabel("y")
 xlabel("x")

 figure(3);
 surfc(x,y,f);
 title ("Quellfunktion");
 ylabel("y")
 xlabel("x")

5.Tutoriumsaufgabe: Epidemiologische Modellierung durch numerische Diskretisierung des Reaktionsdiffusionprozess [11]

Anmerkung: Diese Aufgabe ist in Zusammenarbeit mit Gruppe 3 entstanden.

In der letzten Tutoriumsaufgabe wird das Finite-Differenzen-Verfahren zur Lösung der Reaktionsdiffusionsgleichung

$$\partial _{t}u(x,t)-div\ (c(x)\nabla u(x,t))=f(u(x,t)).$$

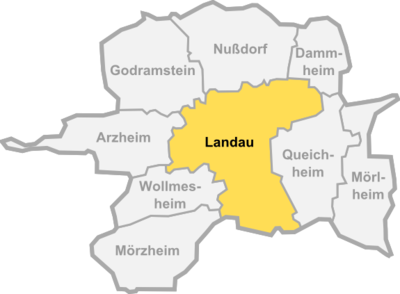
für die zeitlich-räumliche Modellierung der Corona-Ausbreitung auf einem rechteckigen Gebiet D implementiert. In unserem Fall modellieren wir die Corona-Ausbreitung für die Stadt Landau. Die Informationen bezüglich der Fläche und Bevölkerungsdichte von Landau erhalten wir unter folgendem Link: Landau in der Pfalz Wir betrachten in unserer Modellierung die Bevölkerungsdichte für die Kernstadt Landau.

Fläche: 83 km2 (ungefähre Quadratsfläche: 9 km *9 km)
Bevölkerungsdichte in Landau Zentrum: 2619,9 Einwohner pro km2

Von Runkelbold - Eigenes Werk, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=3663743

Festlegung des Gebietes als Gitter

In der Abbildung oben kann man erkennen, dass Landau geographisch grob als Quadrat gesehen werden kann. Mit der bekannten Fläche können dann damit die Kantenlängen festgelegt werden.

 xend=9.0; %in km
 yend=9.0; %in km
 N=60  % Anzahl von Gitterpunkten in x-Richtung(0-te und N-te Index entsprechen den Rändern, keine Gitterpunkte am Rand)
 a=0.01; %konstanter Diffusionskoeffizient %Beschreibt die Verbreitungsgeschwindigkeit(Je größer, desto schneller)
 T=100; %Zeitintervall in Tagen
 delta_t=0.03; %Zeitschritt

Um das Gitter zu konstruieren, muss die Kantenlänge der Quadrates durch $N+1$ geteilt werden, um die $N$ Gitterpunkte in gleichgroßem Abstand auf der Kante zu verteilen, bzw. den Abstand der Gitterpunkte zu berechnen. Da ein Quadrat vorliegt, ist die Anzahl der Gitterpunkte in x- und y-Richtung gleich groß.

 hx=xend/(N+1) %Abstand Gitterpunkte
 hy=hx;        % setze so, damit sich Quadrate bilden
 %M=floor((yend/hy))-1 -> Anzahl der Gitterpunkte in y-Richtung
 M=N; %Im Falle eines Quadrates

 Nr_timesteps=floor (T/delta_t) %Anzahl der Zeitschritte

Parameter für die Reaktionsdiffusionsgleichung

 B=2619,9; %Bevölkerungsdichte Einwohner pro Quadratkilometer(Landau Zentrum)
 k=0.254; %Infektionsrate aus SIR-Abgabe3
 w=1/14;%Wechselrate

Definition der Anfangsfunktion

function wert=initialfunction(x,y)
 wert=0;
 r=0.25; %Fläche des Kreises: 0.20km2   entspricht ca. 523 Einwohnern
 if sqrt((x.-4.5).^2+(y.-4.5).^2)<=r wert=1/(pi*r^2); %Infektionen im Zentrum von Landau (ein Infizierter) 
 endif
endfunction

Systemmatrix

Das erstellte Gitter muss nun um die Randpunkte erweitert werden.

 [x,y]=meshgrid(0:hx:xend,0:hy:yend);
 N=N+2;
 M=M+2;

Die folgende Systemmatrix wird nach dem gleichen Schema wie oben erstellt (siehe Tutoriumsaufgabe 4)

 Vec1=ones(N*M,1); %erzeugt Vektor der Länge N*M
 BB=diag(-4.*Vec1,0)+diag(ones(N*M-1,1),1)+ diag(ones(N*M-1,1),-1)+diag(ones(N*(M-1),1),N)+diag(ones(N*(M-1),1),-N);
%Systemmatrix N^2xN^2 mit -4 auf der Diagonale und 1 auf den Nebendiagonalen und 1 auf der N-ten und -N-ten Nebendiagonale 

 for  i=1:(M-1) 
     BB(i*N+1,i*N)=0;BB(i*N,i*N+1)=0; %Korrektur der Blockmatrix (Blockdiagonalität)
 endfor

 BB=BB*a/hx^2;

Festlegen der Neumann Randbedingungen

Im folgenden sollen die Neumann-Randbedingungen festgelegt werden. Dabei sollen die jeweiligen Ableitungen der Ränder null sein. Dies beschreibt einen freien Fluss der Infizierung in die angerenzenden Gebiete. Für Neumann Randbedingungen auf dem oberen und unteren Rand müssen in unserer Systemmatrix die erste und letzte Blockzeile angepasst werden.

 % Neumann RB für y:   a* partial_y u=0   - einzelne Blöcke der Matrix ersetzen
   block=diag((a/hx)*ones(N,1)); %Matrix mit h bzw. -h auf Diagonale
   %Unterer Rand
   BB(1:N,1:N)=-block;
   BB(1:N,N+1:2*N)=block;
  %Oberer Rand 
  BB(N*(M-1)+1:N*M,N*(M-1)+1:N*M)=-block;
  BB(N*(M-1)+1:N*M,N*(M-2)+1:N*(M-1))=block;

Für Neumann Randbedingungen auf dem linken und rechten Rand müssen die oberste und unterste Zeile unserer Diagonalblöcke von BB ersetzt werden.

 % Neumann RB für x:   a* partial_x u=0 - einzelne Zeilen der Matrix ersetzen
 for i=1:(M-2)
   vector_up=zeros(1,N*M);
   vector_up(N*i+1)=a/hx;
   vector_up(N*i+2)=-a/hx;
   vector_down=zeros(1,N*M);
   vector_down(N*i+N)=a/hx;
   vector_down(N*i+N-1)=-a/hx;
   BB(i*N+1,:)  =-vector_up ; %Vektor der kompletten ersten Zeile   
   BB(i*N+N,:)  =-vector_down ;%Vektor der kompletten letzten Zeile 
 endfor

Graphische Darstellung der Systemmatrix

 figure (67);
 spy (BB);
 xlabel("Spalten")
 ylabel("Zeilen")
 zlabel("Matrix B")
 title ("Systematrix B");

Anfangslösung als Matrix

Durch den Parameter I0 ist die Wahl der Anfangsinfizierungen variabel. Wir gehen in diesem Fall von einem Infizierten im Zentrum von Landau aus.

 I0=1 %Anzahl der Anfangsinfizierungen pro gegebene Fläche pi*r^2
 for  i=1:N
     for j=1:M
      initial(j,i)=I0*initialfunction(x(j,i),y(j,i));
     endfor  
 endfor

 size (initial)
 sol_old=1*reshape(initial',N*M,1);
 %reshape funktioniert Spaltenmäßig: Sp1,Sp2, wir wollen Zeilenmäßig --> Matrix f' ist N(Zeilen) x M (Spalten)

Einlesen der Graphik zur Einwohnerzahl

In diesem Abschnitt wird eine Graphik zur Einwohnerzahl als Bevölkerungsmatrix eingelesen. Danach wählen wir einen für Landau geeigneten Bildausschnitt.

 A=imread ('Monitor_Einwohnerzahl_detail.png');
 size(A); %Zeigt die Dimension der Bildmatrix
 S=A(21:29,16:24);
 imshow (S)  %Bildanzeige
 S=double (S);
 [s1 s2]=size(S);
 Max=max(max(S))
 S=Max-S; %Farbumkehrung/Anpassung

Interpolation der Werte an die Koordinatenmatrix

Die oben aufgestellte Matrix S ist eine 9 x 9 Matrix. Diese Matrix ist allerdings gröber eingeteilt, als unser vorher definiertes Gitter mit viel kleineren Schritten. Das bedeutet, dass wir die Werte von S auf unsere Gitterpunkte interpolieren müssen. Dabei verwenden wir eine zweidimensionale kubische Interpolation.

 Sint=interp2(S,xend*(1*x.+2)/(xend+2),yend*(1*y.+2)/(yend+2), 'cubic');

 Sint=flipud (Sint); %Bild flippen oben <--> unten  
 size (Sint)

 figure(66);
 surface(x,y, (B/Max)*Sint)
 title ("Bevoelkerungsdichte");
 ylabel("y")
 xlabel("x")
 colorbar

 B=reshape((B/Max)*Sint',N*M,1).+0.1*Max; %Angepasste Bevölkerungsdichte  
 size (B)

Bild links: Von Runkelbold - Eigenes Werk, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=3663743

Von Runkelbold - Eigenes Werk, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=3663743

Zwischenfazit Die Gegenüberstellung der beiden Bilder zeigt, dass wir einen geeigneten Ausschnitt unserer Bildmatrix für die Bevölkerungsdichte in Landau gewählt haben. Die Bevölkerungsdichte ist im Zentrum (Kernstadt Landau) am größten und wird in den umliegenden Ortschaften deutlich geringer.

Teil 1: Lösungsschritt - Reaktionsterm für kumulierte Infizierte

Im ersten Teil der Implementierung stellen wir einen Reaktionsterm für die kumulierten Infizierten auf, das heißt, dass wir Infizierte und Genesene betrachten (einmal infiziert, immer infiziert)

Reaktionsterm für kumulierte Infizierte

Im nachfolgenden Reaktionsterm $f({\vec {u}}(t))\approx F({\vec {u}}_{h}(t)):={\frac {k}{\vec {B}}}*{\vec {u}}_{h}(t)*({\vec {B}}-{\vec {u}}_{h}(t))$ wird die Bevölkerungsdichte geographisch differenziert als Funktion einer Raumvariable betrachtet:

 F=@(u) (k./B).*u.*(B.-u);

Dieser Term wird nun zu unserem System von gewöhnlichen Differentialgleichungen des räumlich diskretisierten Neumann-Randwertproblems für die Diffusion hinzugefügt.

Würde man die homogene Differentialgleichung betrachten gilt folgendes:

$\partial _{t}u(x,t)-c\Delta u(x,t)=0$

Dabei lässt sich hier das Stern-Approximationsschema anwenden:

$-c\Delta {\vec {u}}(x,t)\approx A_{h}{\vec {u}}_{h}$

Aus diesem ursprünglichen System ergibt sich also ${\frac {d}{dt}}{\vec {u}}_{h}(t)=-A_{h}{\vec {u}}_{h}(t)$, welches nun zur Reaktionsdiffusionsgleichung ergänzt werden kann:

${\frac {d}{dt}}{\vec {u}}_{h}(t)=-A_{h}{\vec {u}}_{h}(t)+F({\vec {u}}_{h}(t))$.

Zeitschleife

Der numerische Lösungsschritt (Zeitdiskretisierung) erfolgt hier mithilfe des Expliziten Eulerverfahrens: Nach der Anwendung des Vorwärtsdifferenzenquotienten $D_{\Delta t}^{+}{\vec {u}}_{h}(t)={\frac {{\vec {u}}_{h}(t+\Delta t)-{\vec {u}}_{h}(t)}{\Delta t}}\approx {\frac {d{\vec {u}}_{h}(t)}{dt}}$ erhält man folgende Berechnungsformel: ${\vec {u}}_{h}(t_{k+1})={\vec {u}}_{h}(t_{k})+\Delta t{\Big (}-A_{h}{\vec {u}}_{h}(t_{k})+F({\vec {u}}_{h}(t_{k})){\Big )}$, die sich in der implementierten Zeitschleife widerspiegelt:

for i=1:Nr_timesteps
 sol= sol_old+ BB*sol_old*delta_t + 1*F(sol_old)*delta_t;
 sol_old=sol;
 matrix_solution(:,i)=sol; 
endfor

Auswahl an Bildern - jedes fünfte Bild

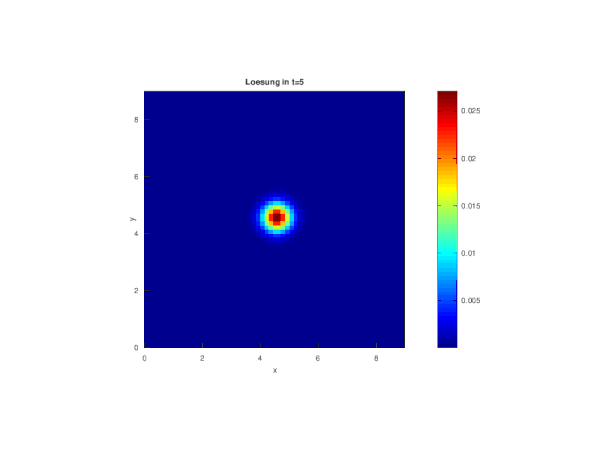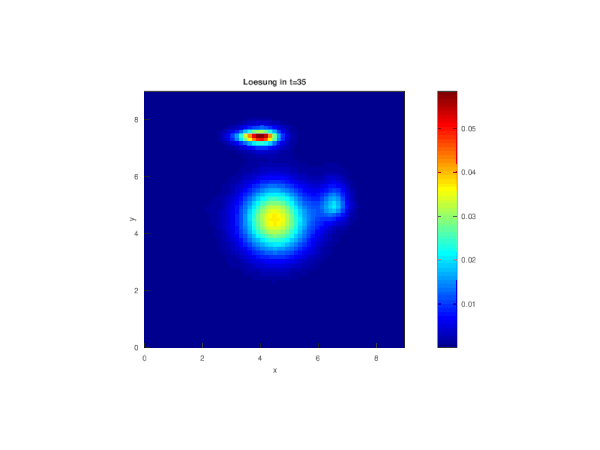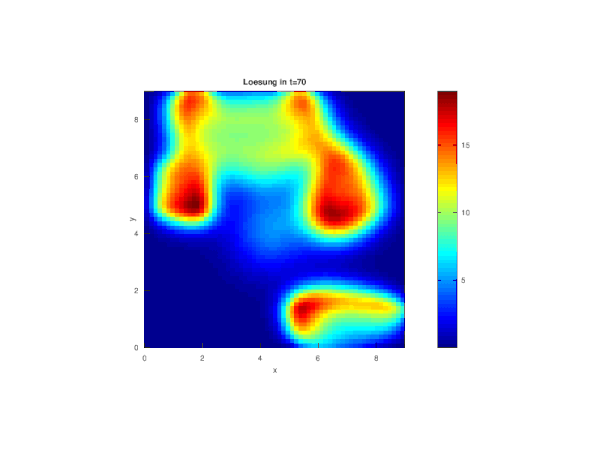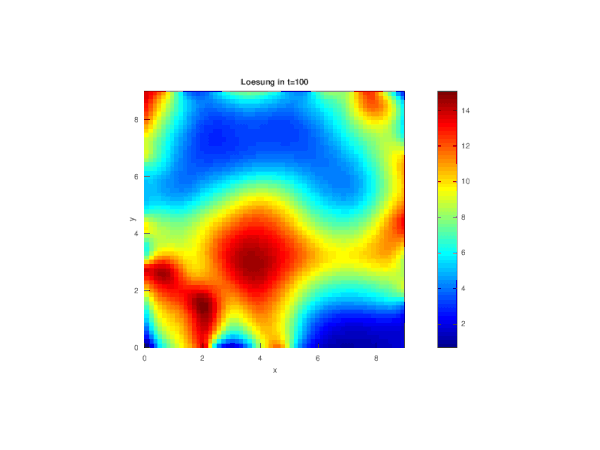
fig_index=floor([0.05:0.05:1]*Nr_timesteps)
j=0
 for i=fig_index
  sol_matrix=reshape(matrix_solution(:,i),N,M);%Matrix mit N(Zeilen) x M(Spalten)
  sol_matrix=sol_matrix';
  disp(['Figure ',num2str(round(i/fig_index(1)))]);
  j=j+1;
  figure(j);
 surface(x,y,sol_matrix*hx^2, "EdgeColor", "none") %multipliziert mit hx^2, damit Anzahl der Infizierten pro Raster und nicht Dichte dargestellt wird
  colormap ("jet")
   axis([0 xend 0 yend 0  1.1*max(max(B))*hx^2]) 
  colorbar 
  title (["Loesung in t=", num2str(round(delta_t*i))]);
  ylabel("y")
  xlabel("x")
  test=["Fig_", num2str(j),".jpg"]
endfor

Anfangslösung

Die Abbildung zeigt, dass wir zu Beginn der Corona-Ausbreitung ca. einen Infizierten im Zentrum haben.

Animation

Teil 2: Lösungsschritt - Reaktionsterm für aktuell Infizierte

In diesem Teil möchten wir die gleiche Implementation wie oben durchführen, aber nun anstatt der kumulierten Infizierten die aktuell Infizierten betrachten. Hierfür benötigen wir unsere Kenntnisse aus dem SIR-Modell. Dabei wird unser SIR-Modell auf die räumliche Verbreitung ausgeweitet, indem der Diffusionsterm hinzugefügt wird. Unsere Funktionen heißen deshalb nicht mehr nur S, I und R, sondern u_S bzw. u_I (u_R wird an dieser Stelle ignoriert) und sind nicht mehr nur von der Zeit t abhängig, sondern auch von einer Raumvariable.

Es werden zwei gekoppelte Reaktionsdiffusionsgleichungen für die Dichtefunktionen $u_{I},\ u_{S}$ gelöst. Die entsprechenden Reaktionsterme sehen wie folgt aus:

$f_{S}({\vec {u}}(t))\approx F_{S}({\vec {u}}_{h}(t)):=-{\frac {c}{\vec {B}}}*{\vec {u_{I}}}_{h}(t)*{\vec {u_{S}}}_{h}(t)$

$f_{I}({\vec {u}}(t))\approx F_{I}({\vec {u}}_{h}(t)):={\frac {c}{\vec {B}}}*{\vec {u_{I}}}_{h}(t)*{\vec {u_{S}}}_{h}(t)-w{\vec {u_{I}}}_{h}(t)$

Vorbereitung der alten Lösung

sol_old=1*reshape(initial',N*M,1); %Aktuell Infizierte
sol_old_susp=B.-sol_old; %Infektionsanfällige

Definition der Slowdown-Funktion

Wir benötigen für den Reaktionsterm eine Slowdown-Funktion. Diese übernehmen wir aus unserer Implementierung des SIR-Modells aus der dritten Tutoriumsaufgabe.

function val=slowdown3(x,t)
if x<t val=1 ; else if x<t +8 val=t./(x.^1.1); else if x<t +16 val=t./(x.^1.25); else if x<t +22 val=t./(x.^1.4); 
else val=t./(x.^1.5);
endif
endif
endif
endif
if x> 61  val=0.5 ; endif %Lockerungen 
endfunction

Reaktionsterm aktuell Infizierte

Nun definieren wir eine nichtlineare Funktion von u (aktuell Infizierte), v (Empfängliche) und der Zeit t.

F=@(u,v,t) (k*slowdown3(25,t)./B).*u.*v;

Zeitschleife

Der Zeitdiskretisierung erfolgt an dieser Stelle auch wieder mithilfe des expliziten Eulerverfahrens.

for i=1:Nr_timesteps
 Reakt=F(sol_old,sol_old_susp, i*delta_t); %Nichtlinearer Term, wird aus alten Werten berechnet in der  Form F=@(u,v,t)  
 sol_susp= sol_old_susp+ BB*sol_old_susp*delta_t - Reakt*delta_t; %Erster Reaktionsterm: Empfängliche
 sol= sol_old+ BB*sol_old*delta_t+ (Reakt-w.*sol_old)*delta_t; %Zweiter Reaktionsterm: Aktuell Infizierte (um Term -w*I erweitert)  

 sol_old=sol; %Speicherung für den nächsten Zeitschritt (alte Lösung wird auf neue Lösung überschrieben)
 sol_old_susp=sol_susp;
 matrix_solution1(:,i)=sol;%Speicherung der aktuell Infizierten in einer Matrix, Speicherung der Anfälligen (S) nicht implementiert
endfor

Animation

Anschließend erhalten wir mit dem gleichen Octave-Befehl wie im ersten Teil unsere Animation für die aktuell Infizierten.

Skripte in Cocalc

Tut1: Kontaktmodell [12]

Tut2: Fundamentallösungen der Poisson und der Diffusionsgleichung [13]

Tut3: Kompartimentmodelle für die dynamische Beschreibung der Infektionsverbreitung und die Datenlage [14]

Tut4: Randwertaufgabe für Poissongleichung mit Finite-Differenzen-Verfahren [15]

Tut5: Epidemiologische Modellierung durch numerische Diskretisierung des Reaktionsdiffusionprozess [16]