Kurs:Stochastik/Galtonbrett

Einführung (1)

Die Abbildung zeigt ein Galtonbrett.

Einführung (2)

Die Abbildung zeigt das Modell eines Galtonbretts.

Einführung (3)

Das Video zeigt ein Galtonbrett.

Einführung (4)

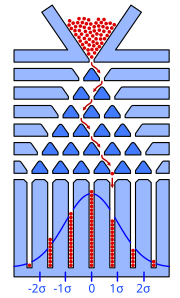
Die Abbildung zeigt ein Galtonbrett mit fallenden Kugeln.

Einführung (5)

Ein Galtonbrett (nach Francis Galton), auch (Galtonsches) Zufallsbrett, ist ein mechanisches Modell zur Demonstration und Veranschaulichung der Binomialverteilung, einer Wahrscheinlichkeitsverteilung, die in vielen Zufallsexperimenten eine Rolle spielt (siehe Konzept vom Galtonbrett).

Mathematische Betrachtung (1)

Jedes Aufprallen einer Kugel auf eines der Hindernisse ist ein Bernoulli-Versuch. Die beiden möglichen Ausgänge sind „Kugel fällt nach rechts“ (X=1) und „Kugel fällt nach links“ (X=0).

Bei symmetrischem Aufbau ist die Wahrscheinlichkeit, nach rechts zu fallen, $P(X=1)=p=1/2$ und die Wahrscheinlichkeit, nach links zu fallen, $P(X=0)=q=1/2$.

Mathematische Betrachtung (2)

Durch unsymmetrischen Aufbau oder durch Schiefstellen des Brettes kann man auch einen anderen Wert für $p$ erreichen, wobei aber natürlich weiterhin $q=1-p$ ist, denn die Kugeln, die nicht nach rechts fallen, fallen nach links. Dieser Fall wird weiter unten besprochen.

Indem die Kugel nach Passieren des ersten Hindernisses auf ein neues trifft, bei dem die gleichen Voraussetzungen gelten, wird hier ein weiterer Bernoulli-Versuch durchgeführt; das Durchlaufen des ganzen Gerätes ist also eine mehrstufige Bernoulli-Kette, wobei die Zahl der waagerechten Reihen von Hindernissen die Länge dieser Kette ist. Im dargestellten Bild handelt es sich um eine 4-malige Wiederholung eines Bernoulli-Versuchs, d. h. eine Bernoulli-Kette der Länge 4.

Mathematische Betrachtung (3)

Mathematische Betrachtung (4)

Man kann nun berechnen, mit welcher Wahrscheinlichkeit eine Kugel in ein bestimmtes der Fächer fällt. Bei nur einem Hindernis (A) ist die Wahrscheinlichkeit 1/2 für links und für rechts, oder, anders formuliert, im Mittel fällt die Hälfte aller Kugeln nach rechts und die Hälfte nach links. Damit trifft jeweils die Hälfte der Kugeln auf B und die andere Hälfte auf C, wo sie sich wieder mit gleichen Wahrscheinlichkeiten nach links und rechts aufteilen. Damit fällt aber nur noch 1/4 der Kugeln an B nach links, 1/4 an C nach rechts, und jeweils 1/4 von links und von rechts in den Zwischenraum zwischen B und C. Hier addieren sich die Wahrscheinlichkeiten also, und 1/4 + 1/4 = 2/4 (= 1/2, aber mit Absicht nicht gekürzt) fällt in der Mitte zwischen B und C hindurch.

Mathematische Betrachtung (5)

Anhand der Abbildung kann man weiter verfolgen, wie der Strom der Kugeln sich an jeder Hindernisreihe aufteilt (an der nächsten wird man daher mit Achteln, an der übernächsten mit Sechzehnteln des Gesamtbestandes rechnen müssen) und sich andererseits in jedem Zwischenraum zwischen zwei benachbarten Hindernissen wieder vereinigt.

Die sich so ergebenden Wahrscheinlichkeiten nach der letzten Aufteilung und Vereinigung an der untersten Hindernisreihe (G,H,I,J) sind die Wahrscheinlichkeiten, mit denen die Kugeln in die Fächer (R,S,T,U,V) fallen.

Mathematische Betrachtung (6)

Im Beispiel haben alle diese Wahrscheinlichkeiten den Nenner 16, da es 4 Reihen von Hindernissen sind (16=2⁴). Die Zähler ergeben sich durch Addieren der Zähler in der Reihe darüber, was der Vereinigung der Kugelströme in den Zwischenräumen entspricht. Damit ergibt sich folgendes Schema für die Wahrscheinlichkeiten:

                  Zähler:        Nenner:
    Reihe 0:         1           = 1 → =2^0              1 =11^0   (Die Potenzreihe der Zahl 11
          1:        1+1          = 2 → =2^1             11 =11^1    bricht nicht ab, wenn die
          2:       1+2+1         = 4 → =2^2            121 =11^2    Zähler ab der 6. Zeile in 
          3:      1+3+3+1        = 8 → =2^3           1331 =11^3    ein anderes Stellenwert-
          4:     1+4+6+4+1       =16 → =2^4          14641 =11^4    system umgerechnet werden.)

Mathematische Betrachtung (7)

Man erkennt, dass die Zähler die Binomialkoeffizienten sind, denn sie entstehen nach dem Schema des Pascalschen Dreiecks. Die Nenner sind Potenzen von 2, sie folgen aus der Wahrscheinlichkeit $p=q=$1/2, nach rechts bzw. links zu fallen.

Die Fächer R,S,T,U,V kann man danach nummerieren, wie oft eine Kugel nach rechts fallen muss, um das jeweilige Fach zu erreichen. Damit bekommt Fach R die Nummer 0, denn eine Kugel, die in R landet, ist keinmal nach rechts gefallen, sondern immer nur nach links. Fach S hat die Nummer 1, denn eine Kugel, die hier landet, ist genau einmal nach rechts gefallen (in der ersten, zweiten, dritten oder vierten Reihe, aber jedenfalls nur dieses eine Mal). Entsprechend bekommen die anderen Fächer die Nummern.

Mathematische Betrachtung (8)

Die Abbildung zeigt das Ergebnis, welches einer Binomialverteilung ähnelt. Da hier die Hohlräume zwischen den Hindernissen im Vergleich zu den Kugeln zu groß gewählt sind, werden manche Kugeln nicht abgelenkt. Dadurch ist das Ergebnis verfälscht und der mittlere Balken wirkt zu hoch.

Mathematische Betrachtung (9)

Die Wahrscheinlichkeit, in das Fach 0 zu fallen, ist

$B(0)=1\cdot \left({\frac {1}{2}}\right)^{4}={\frac {1}{16}}.$

Die Wahrscheinlichkeit, in das Fach 1 zu fallen, ist

$B(1)=4\cdot \left({\frac {1}{2}}\right)^{4}={\frac {4}{16}}.$

Mathematische Betrachtung (10)

Ebenso folgt:

$B(2)=6\cdot \left({\frac {1}{2}}\right)^{4}={\frac {6}{16}},$

$B(3)=4\cdot \left({\frac {1}{2}}\right)^{4}={\frac {4}{16}},$

$B(4)=1\cdot \left({\frac {1}{2}}\right)^{4}={\frac {1}{16}}.$

Mathematische Betrachtung (11)

Allgemein gilt für das Fach $k$:

$B(k)={4 \choose k}\cdot \left({\frac {1}{2}}\right)^{4}={4 \choose k}\cdot {\frac {1}{16}}.$

Hierin ist ${4 \choose k}$ der Binomialkoeffizient in Zeile 4, Spalte $k$ des Pascalschen Dreiecks (Beachte: die Spalten sind die Nummern der Fächer, beginnen also mit 0).

Verallgemeinert man die Formel weiter auf ein Galtonbrett mit $n$ Hindernisreihen (statt 4, wie im Beispiel), also auf eine Bernoulli-Kette der Länge $n$, so wird gelten:

$B(k,n)={n \choose k}\cdot \left({\frac {1}{2}}\right)^{n}={n \choose k}\cdot {\frac {1}{2^{n}}}.$

Mathematische Betrachtung (12)

Zur weiteren Verallgemeinerung stellt man sich nun ein unsymmetrisches Galtonbrett vor, bei dem die Wahrscheinlichkeiten für links und rechts nicht gleich groß sind. Die Kugeln fallen mit der Wahrscheinlichkeit $p$ nach rechts und mit $q=1-p$ nach links.

Mathematische Betrachtung (13)

Mathematische Betrachtung (14)

Dann landen sie in Fach 0 mit der Wahrscheinlichkeit q⁴ statt (1/2)⁴, denn sie müssen immer noch viermal nach links fallen, tun dies aber nun jeweils mit der Wahrscheinlichkeit $q$. <br#>

Im ganz rechten Fach (für das sie viermal nach rechts fallen müssen, was sie mit jeweils der Wahrscheinlichkeit $p$ tun), landen sie mit $p^{4}$.

Mathematische Betrachtung (15)

Galtonbox

Ergebnis bei gekipptem Galtonbrett, Hier beträgt die Wahrscheinlichkeit p ca. 0,9.

Mathematische Betrachtung (16)

Für die anderen Fächer müssen sie der Nummer ($k$) entsprechend $k$ mal nach rechts und die übrigen Male ($4-k$) nach links fallen. Dies tun sie mit den Wahrscheinlichkeiten $p^{k}$ bzw. $q^{4-k}=(1-p)^{4-k}$. Was sich dabei nicht ändert, sind die Vereinigungen der Kugelströme in den Zwischenräumen. Die Binomialkoeffizienten bleiben also unberührt. Die allgemeine Formel für ein 4-reihiges Galtonbrett mit der Wahrscheinlichkeit $p$, nach rechts zu fallen, lautet daher:

$B(k,p,4)={4 \choose k}\cdot p^{k}\cdot q^{4-k}={4 \choose k}\cdot p^{k}\cdot (1-p)^{4-k}.$

Mathematische Betrachtung (17)

Und für die allgemeine Formel eines entsprechend $n$-reihigen Brettes folgt schließlich:

$B(k,p,n)={n \choose k}\cdot p^{k}\cdot q^{n-k}={n \choose k}\cdot p^{k}\cdot (1-p)^{n-k}.$

Dies ist dann genau die Binomialverteilung einer Bernoulli-Kette der Länge $n$ mit $P(1)=p$ und $P(0)=q=1-p$.

Weblinks

 Commons: Galtonbrett – Sammlung von Bildern, Videos und Audiodateien

• Java-Applet zur Veranschaulichung
• Galtonbrett – Physikalische Simulation in HTML5
• Galtonbrett variabel – flexible Simulation inkl. Aufgabenstellungen

Literatur

• Gerd Binnig: Aus dem Nichts. Über die Kreativität von Natur und Mensch. 2. Auflage. Piper, München u. a. 1997, ISBN 3-492-21486-X.
• Sir Francis Galton: Natural inheritance. Macmillan, London 1889 (Enthält die Beschreibung des Galton Bretts).

Seiten-Information

Wikipedia2Wikiversity

Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:

• Galtonbrett https://de.wikipedia.org/wiki/Galtonbrett
• Datum: 11.11.2018
• Wikipedia2Wikiversity-Konverter: https://niebert.github.com/Wikipedia2Wikiversity

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Stochastik' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Stochastik/Galtonbrett
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.