Kurs:Stochastik/Gesetz der großen Zahlen

Einführung

Es gibt mehrere Gesetze der großen Zahlen (z.B. bzgl. unterschiedlicher starken stochastischen Konvergenzaussagen). Dieser Kursinhalt führt in die grundlegenden Prinzipien ein, durch große Anzahl von Versuchswiederholungen eine stochastische Konvergenz gegen ein ggf. unbekannte theoretische Wahrscheinlichkeit zu formalisieren und die mathematische Aussage mit Werkzeugen aus der Wahrscheinlichkeitstheorie zu beweisen.

Visualisierung

Die Abbildung zeigt die Visualisierung des starken Gesetzes der großen Zahlen: Auf der y-Achse ist die relative Häufigkeit einer gewürfelten Sechs aufgetragen, während auf der x-Achse die Anzahl der Durchgänge angegeben ist. Die horizontale graue Linie zeigt die Wahrscheinlichkeit eines Sechserwurfes von ${\frac {1}{6}}$, die schwarze Linie den in einem konkreten Experiment gewürfelten Anteil aller Sechser.

Veranschaulichung

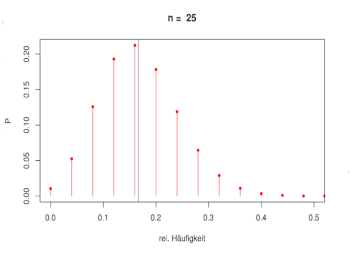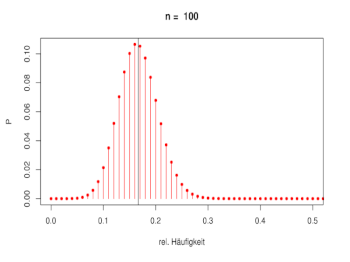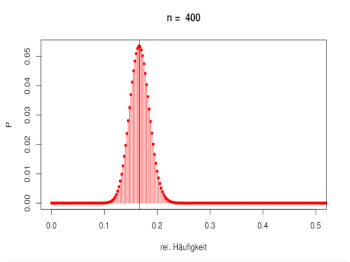
Die Abbildung zeigt die Visualisierung des schwachen Gesetzes der großen Zahlen beim Würfelbeispiel: Für wachsendes n zieht sich die Verteilung der relativen Häufigkeit immer enger auf den Wert 1/6 zusammen.

Stochastische Grenzwertsätze

Als Gesetze der großen Zahlen, abgekürzt GGZ, werden bestimmte Grenzwertsätze der Stochastik bezeichnet.

In ihrer einfachsten Form besagen diese Sätze, dass sich die relative Häufigkeit eines Zufallsergebnisses in der Regel um die theoretische Wahrscheinlichkeit eines Zufallsergebnisses stabilisiert, wenn das zu Grunde liegende Zufallsexperiment immer wieder unter denselben Voraussetzungen durchgeführt wird.

Fehlinterpretation von stochastischer Konvergenz

Die häufig verwendete Formulierung, dass sich die relative Häufigkeit der Wahrscheinlichkeit „immer mehr annähert“ ist dabei irreführend, da es auch bei einer großen Anzahl von Wiederholungen Ausreißer geben kann. Die Annäherung ist also schwächer als punktweise Konvergenz von Funktionenfolgen. Ferner muss bei stochastischer Konvergenz auch unterschiedliche Formen unterscheiden.

Schwache und starke Konvergenzaussagen

Formal handelt es sich um Aussagen über die Konvergenz des arithmetischen Mittels von Zufallsvariablen, zumeist unterteilt in „starke“ (fast sichere Konvergenz) und „schwache“ (Konvergenz in Wahrscheinlichkeit) Gesetze der großen Zahlen.

Einführende Beispiele

Die folgenden Beispiele betrachten das Gesetz der großen Zahlen mit zwei unterschiedlichen Voraussetzungen:

• bekannte theoretische Wahrscheinlichkeit bei einer fairen Münze mit $p={\frac {1}{2}}$
• unbekannte theoretische Wahrscheinlichkeit bei einer verbogenen Münze mit $p=?$ (siehe Aufgabe zur verbogenen Münze/Unterlegscheibe)

Beispiel: Wurf einer fairen Münze

Die Wahrscheinlichkeit, dass eine Münze beim Werfen Kopf zeigt, betrage $p={\frac {1}{2}}$. Je häufiger die Münze geworfen wird, desto unwahrscheinlicher wird es, dass der Anteil der Würfe, bei denen Kopf erscheint (also die relative Häufigkeit des Ereignisses „K“), um mehr als einen beliebigen vorgegebenen Wert $\varepsilon >0$ von der theoretischen Wahrscheinlichkeit $p={\frac {1}{2}}$ abweicht.

Bemerkung - absolute Differenz Kopf-Würfe und halber Gesamtzahl

Dagegen ist es durchaus möglich, dass bei einer konkreten Versuchsreihe die absolute Differenz zwischen der Anzahl der Kopf-Würfe und der halben Gesamtzahl der Würfe anwächst.

Beispiel - wachsende absolute Differenz

Angenommen, eine Serie von Münzwürfen beginne mit „K“, „Z" ("zahl"), „K“, „K“. Dann wurde „K“ bis dahin dreimal geworfen, „Z“ einmal. „K“ hat gewissermaßen einen Vorsprung von zwei Würfen. Nach diesen vier Würfen ist die relative Häufigkeit von „K“ ${\frac {3}{4}}$ , die von „Z“ ${\frac {3}{4}}$. Nach 96 weiteren Würfen stelle sich ein Verhältnis von 47 Mal „Z“ zu 53 Mal „K“ ein. Der Vorsprung von „K“ ist also nach 100 Würfen sogar noch größer als nach vier Würfen, jedoch hat sich der relative Abstand von „K“ und „Z“ stark verringert, beziehungsweise – und das ist die Aussage des Gesetzes der großen Zahlen – der Unterschied der relativen Häufigkeit von „K“ zum Erwartungswert von „K“. Der Wert $\textstyle {\frac {53}{100}}=0{,}53$ liegt sehr viel näher beim Erwartungswert 0,5 als ${\frac {3}{4}}=0,75$.

Bemerkung - Wahrscheinlichkeit von Ausreißern

Insgesamt kann man festhalten, dass bei einem Zufallsexperiment bei ansteigenden Versuchswiederholungen $n$ die absolute Differenz zwischen Trefferanzahl und der theoretisch zu erwartenden Trefferanzahl ansteigen kann. Allerdings die relative Häufigkeit stochastisch gegen die theoretische Wahrscheinlichkeit konvergiert. Dabei wird die Wahrscheinlichkeit von Ausreißern $\geq \varepsilon$ ansteigenden Versuchswiederholungen $n$

Bemerkung - Fehlinterpretation

Insbesondere besagen diese Gesetze der großen Zahlen nicht, dass ein Ereignis, welches bislang unterdurchschnittlich eintrat, seinen „Rückstand“ irgendwann ausgleichen und folglich in Zukunft häufiger eintreten muss. Dies ist ein bei Roulette- und Lottospielern häufig verbreiteter Irrtum, die „säumige“ Zahl müsse nun aber aufholen, um wieder der statistischen Gleichverteilung zu entsprechen. Es gibt daher kein Gesetz des Ausgleichs (siehe auch stochastische Unabhängigkeit).

Schwaches Gesetz für relative Häufigkeiten

Der einfachste Fall eines Gesetzes der großen Zahlen, das schwache Gesetz für relative Häufigkeiten, ist das Hauptergebnis in Jakob I Bernoullis Ars Conjectandi (1713). Ein Zufallsexperiment mit genau zwei Ausgängen, genannt Erfolg und Misserfolg, also ein Bernoulli-Experiment, werde $n$ Mal unabhängig wiederholt. Bezeichnet $p\in (0,1)$ die Erfolgswahrscheinlichkeit bei einer einzelnen Durchführung $X_{k}$ im $k$-ten Versuch, dann ist $X_{1}+\ldots +X_{n}$ als Erfolge nach $n$ Versuchen binomialverteilt mit den Parametern $n$ und $p$.

Relative Häufigkeit

Für die Berechnung der relativen Häufigkeit muss man die Anzahl der Treffer/Erfolge nach $n$ Versuchen noch durch die Anzahl der Versuche teilen. Diese relative Häufigkeit definiert man nun als Zufallsgröße ${\overline {X_{n}}}$ mit:

$R_{n}={\tfrac {1}{n}}\sum _{k=1}^{n}X_{k}$

Stochastische Konvergenz und theoretische Wahrscheinlichkeit

Das schwache Gesetz der großen Zahlen liefert nun eine Aussage über die stochastische Konvergenz der relative Häufigkeit gegen die theoretisch Wahrscheinlichkeit $p$ der Bernoulli-Verteilung. Ist diese $p$ unbekannt (wie z.B. bei einer verbogenen Münze), dann kann man die relative Häufigkeit $R_{n}$ dazu verwenden, die theoretische Wahrscheinlichkeit $p$ durch Erhöhung der Versuchswiederholungen $n$ immer "besser" zu schätzen.

Experiment - Verbogene Münze

Verwenden Sie statt einer Münze eine Unterlegscheibe, die verbiegen Sie verschiedene Scheiben unterschiedlich stark und markieren Sie eine Seite mit einer Farbe oder Filzstift als Trefferseite:

Aufgaben - Verbogene Münze

• Argumentieren Sie, warum die Erfolgswahrscheinlichkeit nun nicht mehr bei $p={\frac {1}{2}}$ liegt und begründen Sie, warum eine der Seiten eine höhere Wahrscheinlichkeit besitzt (z.B. über den Schwerpunkt der verbogenen Unterlegscheibe)
• Führen Sie Versuchswiederholungen durch und nutzen Sie diese, um über die relative Häufigkeit die Trefferwahrscheinlichkeit der unterschiedlichen verbogenen Münzen zu schätzen.
• Simulieren Sie eine solches Experiment mit der OpenSource-Software LibreOffice Calc und der Generierung von Zufallszahlen.

Gesetze der großen Zahlen

Betrachten Sie nun die Beweise zu einzelnen Gesetzen der großen Zahlen:

• Schwaches Gesetz der großen Zahlen
• Starkes Gesetz der großen Zahlen

Geschichte der Gesetze der großen Zahlen

Einen gewissen Abschluss erlangte die Geschichte des starken Gesetzes der großen Zahlen mit dem 1981 bewiesenen Satz von N. Etemadi 1981. Der Satz von Etemadi zeigt die Gültigkeit des starken Gesetzes der großen Zahlen unter der Annahme, dass die Zufallsvariablen integrierbar sind (also einen endlichen Erwartungswert besitzen), jeweils dieselbe Verteilung haben und je zwei Zufallsvariablen unabhängig sind. Die Existenz einer Varianz wird nicht vorausgesetzt.

Literatur

• Jörg Bewersdorff: Statistik – wie und warum sie funktioniert. Ein mathematisches Lesebuch. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1753-2, doi:10.1007/978-3-8348-8264-6.
• Rick Durrett: Probability. Theory and Examples. 3. Auflage. Thomson Brooks/Cole, Belmont CA u. a. 2005, ISBN 978-0-534-42441-1.
• Hans-Otto Georgii: Stochastik. Einführung in die Wahrscheinlichkeitstheorie und Statistik. 4., überarbeitete und erweiterte Auflage. de Gruyter, Berlin u. a. 2009, ISBN 978-3-11-021526-7, doi:10.1515/9783110215274.
• Karl Mosler, Friedrich Schmid: Wahrscheinlichkeitsrechnung und schließende Statistik. 2., verbesserte Auflage. Springer, Berlin u. a. 2006, ISBN 978-3-540-27787-3, doi:10.1007/3-540-29441-4.
• Klaus D. Schmidt: Maß und Wahrscheinlichkeit. Springer, Berlin u. a. 2009, ISBN 978-3-540-89729-3, doi:10.1007/978-3-540-89730-9. 

Siehe auch

• stochastische Unabhängigkeit
• Schwaches Gesetz der großen Zahlen
• Konvergenz nach Wahrscheinlichkeit
• Konvergenz nach Verteilung

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Stochastik' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Stochastik/Gesetz%20der%20gro%C3%9Fen%20Zahlen
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

Wikipedia2Wikiversity

Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:

• Gesetz der großen Zahlen https://de.wikipedia.org/wiki/Gesetz%20der%20gro%C3%9Fen%20Zahlen
• Datum: 17.12.2018
• Wikipedia2Wikiversity-Konverter: https://niebert.github.com/Wikipedia2Wikiversity