Zahlbereichserweiterung
Einleitung
[Bearbeiten]Diese Seite kann als Wiki2Reveal Folien angezeigt werden. Einzelne Abschnitte werden als Folien betrachtet und Änderungen an den Folien wirken sich sofort auf den Inhalt der Folien aus.
Zielsetzung
[Bearbeiten]Diese Lernressource in der Wikiversity hat das Ziel, in das grundlegende Vorgehen einzuführen bei der Erweiterung von Zahlbereichen.
Zahlbereichserweiterung und Lösbarkeit
[Bearbeiten]In dieser Lernressource wird zunächst die Unlösbarkeit von Gleichungen in einem gegebenen Zahlbereich betrachtet. Aus Unlösbarkeit der Gleichung in dem jeweiligen Zahlbereich ergibt sich die Motivation, den Zahlbereich so zu erweitern, dass die betreffende Gleichung in dem erweiterten Zahlbereich lösbar wird.
Von den natürlichen Zahlen zu den ganzen Zahlen
[Bearbeiten]Die folgende Gleichung kann in der Primarstufe formuliert werden. Diese kann formuliert werden kann, die aber in nicht lösbar ist.
Lösbar in dem Zahlbereich mit Lösung .
Bemerkung der Unlösbarkeit von Gleichung
[Bearbeiten]In der Grunndschule wird der Zahlbereich noch nicht erweitert. Allerdings ergibt aus dem Vergleich der folgenden Aufgaben die Motivation für die Begründung, warum man für eine Gleichung eine Zahl 2 findet, die die Gleichung löst und warum die andere Gleichung unlösbar in bleibt.
Von den ganzen Zahlen zu den rationalen Zahlen
[Bearbeiten]Gleichung, die formuliert werden kann, die aber in nicht lösbar ist.
Lösbar in dem Zahlbereich mit Lösung (siehe auch Didaktik der Bruchrechnung[1])
Von den rationalen Zahlen zu den reellen Zahlen
[Bearbeiten]Gleichung, die formuliert werden kann, die aber in nicht lösbar ist.
Lösbar in dem Zahlbereich mit den beiden Lösungen (siehe auch Didaktik der Analysis[2]).
Beweisaufgabe - Wurzel 2 irrational
[Bearbeiten]Zeigen Sie über einen Beweis durch Widerspruch, dass sich nicht als Bruch mit und darstellen lässt.
Von den reellen Zahlen zu den komplexen Zahlen
[Bearbeiten]Gleichung, die formuliert werden kann, die aber in nicht lösbar ist.
Lösbar in dem Zahlbereich mit Lösung .
Aufgaben für Studierende
[Bearbeiten]- Untersuchen Sie den Zahlbereich der Quaternionen. Welche Gemeinsamkeiten und Unterschiede gibt es bei der Erweiterung der reellen Zahlen auf die komplexe Zahlen im Vergleich zu der Erweiterung
- Welcher geometrische Zusammenhang besteht zwischen den Quaternionen und einer rechnerisch eleganten Beschreibung des dreidimensionalen euklidischen Raumes.
Übersicht Zahlbereiche
[Bearbeiten]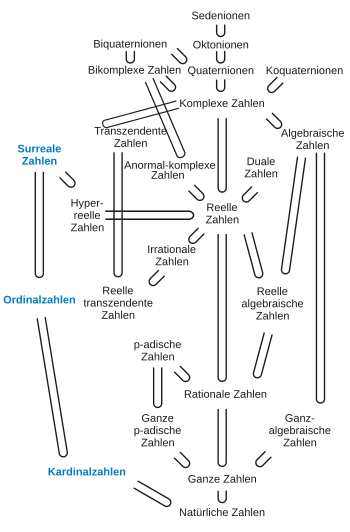
Literatur/Quellennachweise
[Bearbeiten]- ↑ Padberg, F., & Wartha, S. (1978). Didaktik der Bruchrechnung. Freiburg: Herder.
- ↑ Hilger, S. (2018) Didaktik der Analysis - PDF-Skript - URL: https://www.ku.de/fileadmin/150109/Hilger/DAY_WS2018-1.pdf (Abgerufen: 19. Mai 2022, 05:41 UTC)
Siehe auch
[Bearbeiten]
Seiteninformation
[Bearbeiten]Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Wiki2Reveal
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Mathematik' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Zahlbereichserweiterung
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.




















