Gruppenthema 4: Neuronales Netz zur Quantifizierung von Biodiversität
Gruppenmitglieder
[Bearbeiten]- Theresa Haber
- Elias Schüler
- Sarah Tretter
- Lorena Ziegler
Modellierungsthematik
[Bearbeiten]Einleitung
[Bearbeiten]Man schätzt, dass alleine in Deutschland ca. 50.000 verschiedene Tierarten leben. Aufgrund der hohen Artenanzahl ist es schwierig alle Arten zu erkennen und zu zählen. Etwa 7000 der in Deutschland lebenden Tierarten sind gefährdet oder sogar vom Aussterben bedroht und stehen deshalb auf der „Roten Liste“. Der im Mai 2019 veröffentlichte Bericht des Weltbiodiversitätsrates, IPBES [1], geht sogar davon aus, dass in den kommenden Jahrzehnten weltweit eine Millionen Tier- und Pflanzenarten vom Aussterben bedroht sein werden.
Damit würde das 6. Massensterben, seit Beginn des Lebens auf unserer Erde, eingeleitet werden. Die globale Situation der Artenvielfalt ist damit erschreckend. Wie sieht es aber lokal in Deutschland aus? Welche Rolle spielen wir und insbesondere unsere heimische Vogelwelt? Welche Maßnahmen können wir ergreifen um Vogelbestände zu schützen und so die heimische Artenvielfalt auch in Zukunft aufrecht zu erhalten? Damit wir effektiven Vogelschutz betreiben können ist die Analyse des aktuellen Zustands unabdingbar. Folgende Leitfragen sind dabei von höchster Wichtigkeit:
Wie entwickeln sich die Populationen? Wie lautet der prozentuale Anteil einzelner Arten? Zu welchen Zeiten kam es zu Bestandgewinnen oder -verlusten? Wie sieht die örtliche Verteilung aus und wie verändert sich diese? Um diese Fragen beantworten zu können sind Einzelbeobachtungen und Programme des Vogelmonitorings die Grundlage, um so belastbare Forschungsdaten zu erhalten.
Um unser Projekt in die Realität zu übertragen, greifen wir zuletzt auf das Prinzip der neuronalen Netze zurück. Neuronale Netze sind ein Ansatz des maschinellen Lernens, der auf dem Konzept des menschlichen Gehirns basiert. Sie bestehen aus einem Netzwerk von künstlichen Neuronen, die Informationen verarbeiten und Muster erkennen können. Durch das Anpassen der Verbindungen zwischen den Neuronen werden sie trainiert, um komplexe Aufgaben wie das Erkennen von Bildern oder die Vorhersage zukünftiger Ereignisse zu lösen. Neuronale Netze haben in den letzten Jahren enorme Fortschritte gemacht und finden Anwendung in verschiedenen Bereichen der künstlichen Intelligenz.
Biodiversität ist die Vielfalt des Lebens auf der Erde, einschließlich der genetischen Vielfalt, der Vielfalt der Arten und der Vielfalt der Ökosysteme. Alpha-Biodiversität bezieht sich auf die Vielfalt der Arten innerhalb eines bestimmten Gebiets. Es misst die Artenvielfalt vor Ort.
Beta-Biodiversität beschreibt die Unterschiede in der Artenzusammensetzung zwischen verschiedenen Gebieten. Es misst die Veränderungen in der Artenvielfalt beim Wechsel von einem Lebensraum zum anderen.
Die Alpha- und Beta-Biodiversität sind eng miteinander verbunden und ergänzen sich. Die Alpha-Biodiversität trägt zur Beta-Biodiversität bei, da die Vielfalt der Arten in einem bestimmten Gebiet die Grundlage für die Unterschiede in der Artenzusammensetzung zwischen verschiedenen Gebieten bildet. Zusammen liefern Alpha- und Beta-Biodiversität wichtige Informationen über die Gesamtbiodiversität in einer Region und helfen Wissenschaftlern und Naturschutzexperten, die Muster und Prozesse der biologischen Vielfalt besser zu verstehen.
Ziel und Motivation der Modellbildung
[Bearbeiten]Ziel unseres Projektes ist es daher, die Vogelrückgänge und Artengefährdung in Deutschland sowie den Artenzuwachs aufzuzeigen. Anhand des Modellierungsprojekts soll eine Grundlage geschaffen werden zur Quantifizierung von Biodiversität. Hierfür müssen Daten gesammelt, zusammengefasst und ausgewertet werden. Nur auf diese Weise können wir einen Überblick zur aktuellen Situation erhalten, eine Zukunftsprognose aufstellen und gegebenenfalls eingreifen.
In der Sekundarstufe I möchten wir die Schülerinnen und Schüler für die Natur sensibilisieren, sodass sie erkennen, dass die Artenvielfalt nicht selbstverständlich ist und ihnen die Bedeutung der Biodiversität aufzeigen. Mithilfe der Sofwaresysteme Libre Office Calc und Geogebra wollen wir Daten verarbeiten und darstellen. Dies ist unumgänglich für das wissenschaftliche Arbeiten, ebenso für das Weiternutzen der Daten um Heatmaps zu erstellen. Für das Modellierungsprojekt sind auch noch der proportionale Dreisatz, die Prozentrechnung, der Mittelwert und das Erstellen von Diagrammen aus der Unter- und Mittelstufe von Relevanz und können durch unsere Thematik eingeführt und/oder ausgebaut werden.
In der Sekundarstufe II wird es sowohl biologisch, als auch mathematisch anspruchsvoller für die Schülerinnen und Schüler. Hier werden Differenzenfolge und Fehlerfunktion eingeführt, um so eine Prognose für die Zukunft zu erstellen. Ebenfalls wird stochastische (Un-)Abhängigheit eingeführt und in diesem Zusammenhang das Gesetz der großen Zahlen behandelt, um so die Relevanz von Naturschutzgebieten und Wasserstellen aufzuzeigen. Ebenfalls wird die Grundlage gelegt, um einen Algorithmus zu schreiben. Mithilfe eines semantisches Netzes, indem auch Matrizen zu finden sind. Hier kann gegebenenfalls auch schon ansatzweise mit gewichteten Graphen gearbeitet werden, je nachdem wie wichtig das Item zum Vogelmonitoring ist.
Auf dem Niveau der Universität kann das semantische Netze erneut aufgenommen werden und mit komplexeren Matrizen, sowie mit gewichteten Graphen erweitert werden. Ebenso sollte für den Algorithmus die Konfidenzintervalle zur Fehlerkorrektur eingefügt werden. Ebenfalls werden hier die Heatmaps wieder aufgegriffen, indem mit einer in Maxima dreidimensionalen Dichtefunktion gearbeitet wird und diese auch integriert wird.
Zuordnung von Nachhaltigkeitszielen
[Bearbeiten]
Die Sustainable Development Goals (SDGs) sind Leitlinien für weltweite nachhaltige Entwicklung. Die 17 Ziele umfassen soziale Gleichberechtigung, nachhaltiges Wirtschaftswachstum und Umwelt- und Klimaschutz.
- [1] SDG 9: Industry, Innovation and Infrastructure
Unser Projekt zielt vorallem darauf ab, das Vogelmonitorung zu optimieren um so die Forschung zu stärken und den Zugangs zur Informations- und Kommunikationstechnologie zu erweitern. Durch die erweiterte Datenübersicht kann besser über die nachhaltigere Infrastuktur geforscht werden und innovativere Ideen gefunden werden, um das Vogelsterben vorzubeugen.[2]
- [2] SDG 13: Climate Action
Der Klimawandel spielt eine erhebliche Rolle für das Artensterben und die Biodiversität der Vögel, da auf diese Weise nicht nur Habitate zerstört werden, sondern durch das große Insektensterben die Nahrungsgrundlage fehlt. Aus diesem Grund ist es besonders wichtig für unsere Vögel, dass wir Klimaschutzmaßnahmen ergreifen und wir Naturschutzgebiete ausbauen und aufforsten. [3]
- [3] SDG 15: Life on Land
Das SDG 15 Leben an Land ist ein zentrales Ziel unseres Projektes. Denn für die deutschen Vogelbestände ist es unabdingbar die Landökosysteme zu schützen und ihre nachhaltige Nutzung zu fördern. Wir müssen Wälder nachhaltig bewirtschaften, Bodendegradation beenden und umkehren, um so den Verlust der heimischen Vogelbestände zu verhindern und die Vielfalt zu schützen.[4]
Wiki2Reveal
[Bearbeiten]- Motivation und Ziele - (Foliensatz)

- Zuordnung der Nachhaltigkeitsziele-(Foliensatz)

- Modellierungszyklus Sekundarstufe I-(Foliensatz)

- Modellierungszyklus Sekundarstufe II-(Foliensatz)

- Modellierungszyklus Universität-(Foliensatz)

Modellierungszyklen
[Bearbeiten]Datenerhebung
[Bearbeiten]Als Grundlage für den Modellierungszyklus wurden Daten zur Übersicht der Bestandsituation in Deutschland verwendet. Um das Ziel unsere Modellierung zu erreichen, müssen wir herausfinden, wie sich die Populationen unserer Vogelarten entwickeln. Die genaue Anzahl bestimmter Vogelarten ist jedoch aufgrund der großen Anzahl, Artenvielfalt, Größe des Lebensraums, Bewegung der Vögel und vieler anderer Faktoren nahezu unmöglich. Um jedoch möglichst genaue und realistische Werte zu bekommen haben wir die öffentlich zugänglichen Daten von NABU [5], dem Naturschutzbund Deutschland, genutzt.
NABU ist der mitgliederstärkste Umweltverband in Deutschland und setzt sich neben dem Naturschutz auch für die Forschung ein. Eine von der NABU ins Leben gerufene Aktion ist die „Stunde der Gartenvögel“. Diese findet einmal jährlich im Frühjahr statt. Dabei werden deutschlandweit, von freiwilligen Teilnehmern, die gesichteten Vögel gezählt. Der NABU sammelt die ganzen Vogelsichtungen und stellt die Daten online zur Verfügung. Ziel der „Stunde der Gartenvögel“ ist es die aktuelle Vogelbestandssituation in Deutschland zu erfassen. Über einen längeren Zeitraum betrachtet ist es dem NABU so möglich, verschiedene Trends zu erkennen. Diese Daten haben auch wir genutzt, um den Schüler und Schülerinnen den aktuellen Vogelbestand und dessen Verlauf über die letzten und zukünftigen Jahre aufzuzeigen.
Modellierungszyklus 1- Niveau Sekundarstufe 1
[Bearbeiten]Einführung
[Bearbeiten]Um das Thema Biodiversität einzuführen, ist es wichtig, zuerst eine Definition zu geben und einen allgemeinen Überblick zu vermitteln. Anschließend kann eine Übersicht über die Vogelarten und Vogelanzahl in Deutschland bzw. in deutschen Gärten gegeben werden, wobei auch deren visuelle Merkmale hervorgehoben werden, um den Schülern und Schülerinnen eine Grundlage für die Artenbestimmung zu bieten.
Es ist ebenso wichtig, im Rahmen dieser Unterrichtseinheit über die Ungenauigkeit der absoluten Artenanzahl zu sprechen und die Probleme bei Bestimmungen und Zählungen zu verdeutlichen. Dabei können auch die Grenzen dieses Themas aufgezeigt werden, ohne den Unterricht zu beeinträchtigen. Die Schüler und Schülerinnen sollten auch in der Lage sein, mit Dezimalzahlen umzugehen und Texte angemessen zu verstehen, da Daten aus Artikeln oder ähnlichen Quellen analysiert werden sollen. Darüber hinaus sollten sie in der Lage sein, den Mittelwert zu berechnen, was jedoch im Verlauf der Unterrichtsreihe erlernt werden kann.
Ebenso wichtig ist das Arbeiten mit Tabellenkalkulationsprogrammen sowie GeoGebra. Dies ermöglicht den Schülern und Schülerinnen, wichtige Informationen anhand von Tabellen und insbesondere Diagrammen auf einen Blick zu erfassen und damit zu arbeiten. Der mathematische Schwerpunkt der Unterrichtsreihe liegt darin, Diagramme zu erstellen, sie zu lesen, ihre Aussagen zu interpretieren und sie mit anderen Diagrammen zu vergleichen. Es ist von zentraler Bedeutung, dass die Schüler und Schülerinnen mit der Software vertraut werden, darin arbeiten, eigene Ergebnisse produzieren und die Endprodukte verstehen können.
Mathematische Theorie
[Bearbeiten]Mittelwert
Das arithmetische Mittel ist eine mathematische Methode, um den Durchschnitt einer Menge von Zahlen zu berechnen. Es wird auch als Durchschnittswert bezeichnet. Um das arithmetische Mittel zu berechnen, werden alle Zahlen einer Menge zu einer Summe addiert und durch die Anzahl der Zahlen geteilt.
proportionaler Dreisatz
Der proportionale Dreisatz ist ein Lösungsverfahren, das aus mindestens zwei proportional zusammenhängenden Größen eine neue berechnet.[6]
Rechenverfahren: Gegeben seien die proportional zusammenhängenden Größen A und B. Somit entsprechen a Einheiten von A also b Einheiten von B, da sie proportional zueinander sind. Möchte man nun den Anteil c von A im Verhältnis zu B berechnen kann dazu folgende Tabellen genutzt werden:
| Größe A | Größe B | Rechenschritt |
|---|---|---|
| A | b | :a |
| 1 | b:a | :c |
| C | cx (b:a) |

Prozentrechnung
Prozente geben an in welchem Verhältnis zwei Größen zueinander stehen. In der Prozentrechnung unterscheidet man folgende drei Begriffe[7]:
- (1) Der Grundwert G ist die Ausgangsgröße = 100%[8]
- (2) Der Prozentsatz p ist der Anteil des Grundwertes in %[9]
- (3) Der Prozentwert W bezeichnet die Zahl, die den Anteil von G angibt[10]
- Die zugehörige Formel lautet:
Durch das Umstellen der Formel können gegebenenfalls auch der Prozentwert oder der Grundwert berechnet werden.
Diagramme erstellen
Das Erlernen des Erstellens von Diagrammen ist von großer Bedeutung, da Diagramme eine effektive Methode sind, um Daten visuell darzustellen und Informationen zu präsentieren. Diagramme bieten eine anschauliche Möglichkeit, komplexe Daten zu organisieren, zu analysieren und zu kommunizieren. Hier sind einige Gründe, warum es wichtig ist, das Erstellen von Diagrammen zu erlernen:
- um komplexe Daten zu analysieren und Muster, Trends oder Abweichungen auf einen Blick zu erkennen
- das Erstellen von Diagrammen ermöglicht eine klare und prägnante Kommunikation von Informationen, unabhängig von Sprachbarrieren oder Fachkenntnissen
- Diagramme erleichtern die Entscheidungsfindung, indem sie komplexe Informationen vereinfachen, Beziehungen verdeutlichen und alternative Lösungen bewerten
- Diagramme nutzen die visuelle Natur des Menschen, um Daten ansprechend zu präsentieren und Informationen besser im Gedächtnis zu behalten
- das Beherrschen des Erstellens von Diagrammen ist eine wertvolle Fähigkeit in verschiedenen beruflichen Bereichen und verbessert die Datenkompetenz sowie die Effektivität bei der Datenanalyse und -präsentation
Empirisches Gesetz der großen Zahlen
Führt man ein Zufallsexperiment oft aus, so stabilisieren sich die relativen Häufigkeiten rn(A) eines Ereignisses A um einen bestimmten Wert. Diesen bezeichnet man als Wahrscheinlichkeit des Ereignisses A. Es handelt sich hierbei jedoch um eine Erfahrungstatsache, die nicht mathematisch beweisbar ist. Es ist relevant für die Schülerinnen und Schüler, die Wahrscheinlichkeiten zu verstehen, um Prognosen zu stellen und fundierte Entscheidungen zu treffen, basierend auf wiederholten Experimenten und der Genauigkeit der Ergebnisse.[11]
Bezug zum Rahmenlehrplan
[Bearbeiten]Eingeordnet wird in den Rahmenlehrplan Mathematik Sekundarstufe I des Landes Rheinland- Pfalz aus dem Jahr 2007.
- L1 : Zahl und Zahlenbereich [12]
--> Prozentrechnung --> Bruchzahlen berechnen, vergleichen und ordnen
- L5: Daten und Zufall
--> Datenerhebung planen, durchführen und auswerten --> grafische Darstellungen interpretieren
Der mathematische Zusammenhang kann in den Lehrplan der Sekundarstufe I integriert werden, speziell im Rahmen des Rahmenlehrplans Mathematik Rheinland-Pfalz von 2007.
Der Modellierungszyklus konzentriert sich auf den Bereich "L1: Zahl und Zahlbereiche" mit dem Unterthema "Prozent- und Zinsrechnung". Dies beinhaltet die Anwendung der Prozentrechnung in komplexen Sachsituationen. Aus diesem Grund kann der Modellierungszyklus den Klassenstufen 7 und/oder 8 der Sekundarstufe I zugeordnet werden.
Für den Modellierungszyklus der Sekundarstufe I können folgende Ziele den Unterricht strukturieren:
- Entwicklung grundlegender Vorstellungen des Prozentbegriffs
- Lösung von Grundaufgaben der Prozentrechnung, auch im Kopf
- Anwendung der Prozent- und Zinsrechnung in Sachsituationen
Modellierung
[Bearbeiten]Ausarbeitungen der Schüler und Schülerinnen im Vergleich zu öffentlichen Daten
[Bearbeiten]Nachdem die Schülerinnen und Schülern nun Einsichten in das Thema der Biodiversität erhalten haben und Grundlagen in der Vogelbestimmung beherrschen, haben diese nun die Aufgabe innerhalb von 14 Tagen täglich ihr Vogelsichtungen zu zählen und notieren. Zur Zählung wurden 5 Vogelarten ausgewählt und deren markanten Merkmale erarbeitet. Die Ergebnisse wurden mit Hilfe einer Tabellenkalkulation von jedem Schüler und jeder Schülerin festgehalten. Mit Hilfe der Tabellenkalkulation konnte der Mittelwert der Klasse ausgerechnet werden. Später wurden die Ergebnisse der Klasse zusammengetragen und verglichen (beispielhaft nur 10 Schülerinnen und Schüler).
Um den Schülern und Schülerinnen den mathematischen Hintergrund ihrer ersten Berechnungen näherzubringen, werden bekannte Rechenoperationen und einfache Veranschaulichungen verwendet, die ihnen helfen sollen. Anhand einer Tabelle übertragen die Schülerinnen und Schüler ihre Punkte in ein selbst gewähltes Koordinatensystem und verbinden sie miteinander. Um die eigenen Ergebnisse mit denen der gesamten Klassen zu vergleichen, wird der Mittelwert der Klasse ebenfalls in das Koordinatensystem eingezeichnet. Die Funktionsgraphen können mithilfe von GeoGebra bearbeitet und verglichen werden.
Diese Daten wiederum vergleichen die Schülerinnen und Schüler mit den offiziellen Daten von Rheinland-Pfalz und den Zählungen in Landau in der Pfalz. Mit diesem Vergleich wird ihnen das Gesetz der großen Zahlen bewusst und wie wichtig es ist, viele Vogelbeobachter zu mobilisieren, um die Daten so genau wie möglich zu gestalten. Im Folgenden mehrere Beispielvögel, wie die Schülerinnen und Schüler sowohl die Tabelle als auch die Graphen erstellen können.
Hausspatz

| Tage | Schüler 1 | Schüler 2 | Schüler 3 | Schüler 4 | Schüler 5 | Schüler 6 | Schüler 7 | Schüler 8 | Schüler 9 | Schüler 10 | Mittelwert | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 2 | 1,9 | |
| 2 | 3 | 2 | 3 | 3 | 3 | 2 | 3 | 3 | 2 | 3 | 2,7 | |
| 3 | 2 | 1 | 1 | 2 | 2 | 2 | 2 | 1 | 3 | 4 | 2 | |
| 4 | 2 | 2 | 3 | 1 | 2 | 2 | 1 | 2 | 2 | 2 | 1,9 | |
| 5 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 3 | 2 | 1,2 | |
| 6 | 0 | 1 | 2 | 2 | 1 | 2 | 2 | 2 | 3 | 3 | 1,8 | |
| 7 | 0 | 1 | 1 | 1 | 3 | 1 | 1 | 2 | 2 | 2 | 1,4 | |
| 8 | 2 | 2 | 3 | 1 | 2 | 1 | 2 | 3 | 1 | 0 | 1,7 | |
| 9 | 3 | 3 | 3 | 0 | 1 | 0 | 3 | 2 | 2 | 0 | 1,7 | |
| 10 | 1 | 1 | 2 | 0 | 1 | 0 | 2 | 3 | 3 | 1 | 1,4 | |
| 11 | 3 | 1 | 1 | 2 | 2 | 2 | 1 | 2 | 2 | 0 | 1,6 | |
| 12 | 2 | 2 | 2 | 3 | 1 | 1 | 2 | 1 | 1 | 2 | 1,7 | |
| 13 | 4 | 1 | 1 | 1 | 1 | 3 | 3 | 1 | 2 | 1 | 1,8 | |
| 14 | 2 | 1 | 2 | 2 | 1 | 2 | 2 | 2 | 1 | 0 | 1,5 | |
| Mittelwerte | 1,928571429 | 1,571428571 | 1,857142857 | 1,5 | 1,642857143 | 1,428571429 | 1,928571429 | 1,928571429 | 2 | 1,571428571 | 1,735714286 |

Vorgegeben werden folgende Werte, mit denen die Schülerinnen und Schüler ihre Daten vergleichen:
- Sichtungen des Haussperlings im Schnitt in RLP: 6,17
- Sichtungen des Haussperlings im Schnitt in Landau in der Pfalz: 7,07
Kohlmeise

| Tage | Schüler 1 | Schüler 2 | Schüler 3 | Schüler 4 | Schüler 5 | Schüler 6 | Schüler 7 | Schüler 8 | Schüler 9 | Schüler 10 | Mittelwert |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 3 | 1 | 3 | 3 | 2 | 2 | 2 | 3 | 2,3 |
| 2 | 4 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 2,6 |
| 3 | 3 | 3 | 3 | 3 | 3 | 2 | 4 | 2 | 3 | 2 | 2,8 |
| 4 | 2 | 4 | 3 | 2 | 1 | 3 | 3 | 2 | 2 | 2 | 2,4 |
| 5 | 4 | 1 | 4 | 1 | 2 | 2 | 2 | 1 | 4 | 3 | 2,4 |
| 6 | 5 | 1 | 1 | 1 | 2 | 2 | 2 | 1 | 3 | 4 | 2,2 |
| 7 | 2 | 2 | 1 | 2 | 4 | 1 | 3 | 2 | 3 | 3 | 2,3 |
| 8 | 3 | 3 | 2 | 3 | 3 | 2 | 2 | 3 | 4 | 3 | 2,8 |
| 9 | 3 | 2 | 3 | 3 | 3 | 2 | 1 | 3 | 4 | 1 | 2,5 |
| 10 | 2 | 3 | 2 | 4 | 4 | 4 | 2 | 3 | 2 | 2 | 2,8 |
| 11 | 1 | 1 | 4 | 3 | 3 | 3 | 1 | 2 | 1 | 1 | 2 |
| 12 | 1 | 2 | 2 | 2 | 4 | 4 | 2 | 2 | 2 | 2 | 2,3 |
| 13 | 2 | 3 | 1 | 3 | 4 | 3 | 3 | 1 | 3 | 2 | 2,5 |
| 14 | 3 | 2 | 1 | 3 | 3 | 2 | 2 | 2 | 2 | 1 | 2,1 |
| Mittelwerte | 2,642857143 | 2,214285714 | 2,285714286 | 2,357142857 | 2,928571429 | 2,5 | 2,285714286 | 2,071428571 | 2,714285714 | 2,285714286 | 2,428571429 |

Vorgegeben werden folgende Werte, mit denen die Schülerinnen und Schüler ihre Daten vergleichen:
- Sichtungen von Kohlmeisen im Schnitt in RLP: 2,55
- Sichtungen von Kohlmeisen im Schnitt in Landau in der Pfalz: 2,22
Amsel

| Tage | Schüler 1 | Schüler 2 | Schüler 3 | Schüler 4 | Schüler 5 | Schüler 6 | Schüler 7 | Schüler 8 | Schüler 9 | Schüler 10 | Mittelwert |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0 | 1 | 3 | 1 | 2 | 2 | 3 | 2 | 2 | 1,8 |
| 2 | 1 | 2 | 3 | 2 | 3 | 1 | 1 | 2 | 3 | 1 | 1,9 |
| 3 | 2 | 1 | 2 | 0 | 2 | 2 | 2 | 3 | 2 | 2 | 1,8 |
| 4 | 3 | 2 | 1 | 1 | 2 | 3 | 3 | 2 | 1 | 1 | 1,9 |
| 5 | 3 | 0 | 2 | 2 | 4 | 3 | 2 | 2 | 2 | 1 | 2,1 |
| 6 | 2 | 2 | 4 | 3 | 3 | 2 | 1 | 1 | 3 | 1 | 2,2 |
| 7 | 2 | 3 | 3 | 3 | 2 | 2 | 2 | 1 | 2 | 2 | 2,2 |
| 8 | 1 | 1 | 2 | 2 | 1 | 1 | 3 | 0 | 1 | 3 | 1,5 |
| 9 | 2 | 2 | 1 | 2 | 0 | 2 | 2 | 2 | 2 | 1 | 1,6 |
| 10 | 1 | 1 | 2 | 2 | 2 | 1 | 1 | 0 | 2 | 2 | 1,4 |
| 11 | 2 | 2 | 2 | 2 | 1 | 2 | 1 | 2 | 2 | 2 | 1,8 |
| 12 | 2 | 4 | 1 | 1 | 2 | 3 | 2 | 1 | 1 | 1 | 1,8 |
| 13 | 1 | 3 | 2 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1,7 |
| 14 | 2 | 2 | 2 | 3 | 1 | 1 | 1 | 3 | 0 | 1 | 1,6 |
| Mittelwerte | 1,857142857 | 1,785714286 | 2 | 2 | 1,785714286 | 1,928571429 | 1,714285714 | 1,714285714 | 1,714285714 | 1,571428571 | 1,807142857 |

Vorgegeben werden folgende Werte, mit denen die Schülerinnen und Schüler ihre Daten vergleichen:
- Sichtungen von Amseln im Schnitt in RLP: 2,84
- Sichtungen von Amseln im Schnitt in Landau in der Pfalz: 2,37
Rotkehlchen

| Tage | Schüler 1 | Schüler 2 | Schüler 3 | Schüler 4 | Schüler 5 | Schüler 6 | Schüler 7 | Schüler 8 | Schüler 9 | Schüler 10 | Mittelwert |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 2 | 1,9 |
| 2 | 2 | 2 | 3 | 3 | 3 | 2 | 3 | 3 | 2 | 3 | 2,6 |
| 3 | 3 | 1 | 1 | 2 | 2 | 2 | 2 | 1 | 3 | 4 | 2,1 |
| 4 | 2 | 2 | 3 | 3 | 2 | 2 | 1 | 2 | 2 | 2 | 2,1 |
| 5 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 3 | 2 | 1,2 |
| 6 | 2 | 1 | 2 | 2 | 1 | 2 | 2 | 3 | 2 | 3 | 2 |
| 7 | 3 | 1 | 1 | 1 | 3 | 1 | 1 | 2 | 2 | 2 | 1,7 |
| 8 | 2 | 2 | 3 | 1 | 2 | 2 | 2 | 4 | 2 | 0 | 2 |
| 9 | 1 | 3 | 3 | 0 | 1 | 4 | 3 | 1 | 3 | 0 | 1,9 |
| 10 | 2 | 1 | 2 | 0 | 1 | 2 | 2 | 3 | 4 | 1 | 1,8 |
| 11 | 1 | 1 | 1 | 2 | 2 | 2 | 1 | 2 | 1 | 0 | 1,3 |
| 12 | 2 | 2 | 2 | 3 | 1 | 1 | 2 | 2 | 1 | 2 | 1,8 |
| 13 | 3 | 1 | 1 | 1 | 1 | 3 | 3 | 1 | 2 | 1 | 1,7 |
| 14 | 2 | 1 | 2 | 2 | 1 | 2 | 2 | 2 | 1 | 0 | 1,5 |
| Mittelwerte | 2 | 1,571428571 | 1,857142857 | 1,642857143 | 1,642857143 | 1,928571429 | 1,928571429 | 2,071428571 | 2,071428571 | 1,571428571 | 1,828571429 |

Vorgegeben werden folgende Werte, mit denen die Schülerinnen und Schüler ihre Daten vergleichen:
- Sichtungen von Rotkehlchen im Schnitt in RLP: 0,63
- Sichtungen von Rotkehlchen im Schnitt in Landau in der Pfalz: 0,37
Elster

| Tage | Schüler 1 | Schüler 2 | Schüler 3 | Schüler 4 | Schüler 5 | Schüler 6 | Schüler 7 | Schüler 8 | Schüler 9 | Schüler 10 | Mittelwert |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 2 | 0 | 1 | 1,5 |
| 2 | 1 | 2 | 3 | 3 | 3 | 3 | 2 | 1 | 0 | 2 | 2 |
| 3 | 2 | 1 | 1 | 2 | 1 | 1 | 0 | 1 | 0 | 3 | 1,2 |
| 4 | 1 | 1 | 2 | 1 | 2 | 2 | 0 | 3 | 2 | 1 | 1,5 |
| 5 | 1 | 1 | 0 | 2 | 3 | 2 | 0 | 2 | 1 | 1 | 1,3 |
| 6 | 1 | 1 | 0 | 2 | 2 | 2 | 1 | 1 | 0 | 2 | 1,2 |
| 7 | 0 | 1 | 1 | 2 | 1 | 1 | 2 | 1 | 2 | 1 | 1,2 |
| 8 | 0 | 0 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 0 | 0,9 |
| 9 | 0 | 2 | 3 | 1 | 0 | 1 | 1 | 0 | 3 | 0 | 1,1 |
| 10 | 0 | 0 | 1 | 1 | 0 | 3 | 0 | 2 | 1 | 1 | 0,9 |
| 11 | 1 | 1 | 1 | 2 | 2 | 2 | 1 | 1 | 1 | 2 | 1,4 |
| 12 | 2 | 2 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 1,1 |
| 13 | 1 | 0 | 0 | 0 | 2 | 1 | 0 | 1 | 1 | 2 | 0,8 |
| 14 | 2 | 1 | 2 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| Mittelwerte | 1 | 1,071428571 | 1,285714286 | 1,357142857 | 1,571428571 | 1,642857143 | 0,714285714 | 1,285714286 | 1,071428571 | 1,214285714 | 1,221428571 |

Vorgegeben werden folgende Werte, mit denen die Schülerinnen und Schüler ihre Daten vergleichen:
- Sichtungen von Elstern im Schnitt in RLP: 1,83
- Sichtungen von Elstern im Schnitt in Landau in der Pfalz: 1,33
Blaumeise

| Tage | Schüler 1 | Schüler 2 | Schüler 3 | Schüler 4 | Schüler 5 | Schüler 6 | Schüler 7 | Schüler 8 | Schüler 9 | Schüler 10 | Mittelwert |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 2 | 2 | 2 | 2 | 3 | 4 | 1 | 2 | 1 | 2,4 |
| 2 | 4 | 6 | 3 | 4 | 4 | 4 | 2 | 2 | 3 | 3 | 3,5 |
| 3 | 3 | 3 | 2 | 5 | 5 | 2 | 3 | 4 | 0 | 5 | 3,2 |
| 4 | 5 | 3 | 2 | 3 | 3 | 5 | 4 | 2 | 4 | 2 | 3,3 |
| 5 | 2 | 2 | 1 | 6 | 4 | 4 | 2 | 3 | 2 | 4 | 3 |
| 6 | 4 | 4 | 4 | 4 | 2 | 3 | 3 | 1 | 1 | 3 | 2,9 |
| 7 | 3 | 3 | 3 | 3 | 4 | 4 | 5 | 3 | 3 | 2 | 3,3 |
| 8 | 2 | 1 | 2 | 2 | 1 | 3 | 3 | 4 | 5 | 3 | 2,6 |
| 9 | 4 | 3 | 2 | 4 | 3 | 2 | 2 | 2 | 6 | 1 | 2,9 |
| 10 | 6 | 2 | 1 | 5 | 2 | 1 | 3 | 4 | 4 | 4 | 3,2 |
| 11 | 2 | 4 | 4 | 1 | 4 | 3 | 1 | 2 | 3 | 3 | 2,7 |
| 12 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 5 | 2 | 2,6 |
| 13 | 2 | 3 | 2 | 4 | 1 | 4 | 3 | 5 | 2 | 1 | 2,7 |
| 14 | 3 | 2 | 3 | 2 | 0 | 2 | 4 | 2 | 2 | 3 | 2,3 |
| Mittelwerte | 3,428571429 | 2,928571429 | 2,428571429 | 3,357142857 | 2,642857143 | 3 | 2,928571429 | 2,642857143 | 3 | 2,642857143 | 2,642857143 |

Vorgegeben werden folgende Werte, mit denen die Schülerinnen und Schüler ihre Daten vergleichen:
- Sichtungen von Blaumeisen im Schnitt in RLP: 1,7
- Sichtungen von Blaumeisen im Schnitt in Landau in der Pfalz: 1,04
Arbeiten mit öffentlichen Sichtungsdaten
[Bearbeiten]Mit Hilfe des Zugangs zur NABU Datenbank konnten die Schüler und Schülerinnen in einer Gruppenarbeit die Entwicklung bestimmter Gartenvögel der letzten 17 Jahre tabellarisch und graphisch darstellen. Die Schülerinnen und Schüler tragen die Werte in einer Tabellenkalkulation ein und erstellen mit Hilfe dieser Tabelle einen Zugehörigen Graphen. Ziel ist es hier ebenfalls die Daten zu vergleichen und die Ergebnisse zu deuten. Sie sollten in der Lage sein dies mit Open Source Programmen zu bearbeiten.
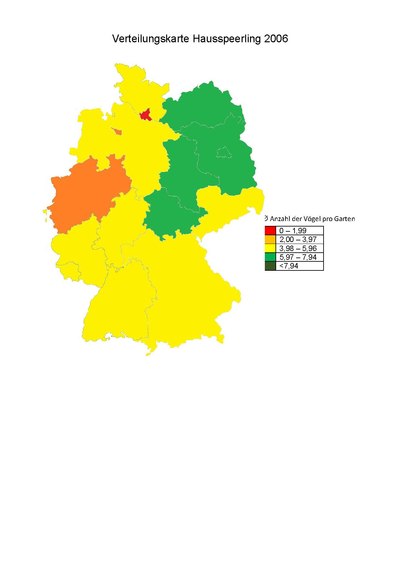
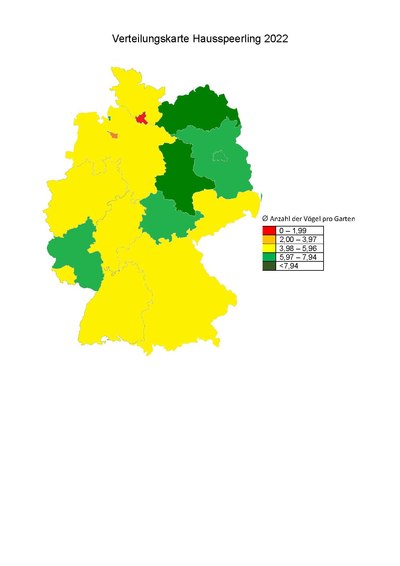
Die folgenden Tabellen und dazugehörigen Graphen zeigen die Entwicklung bestimmter Gartenvögel über die letzten 17 Jahre (2006-2022). Die Daten beziehen sich auf die Sichtungen während der "Stunde der Gartenvögel". Dargestellt werden die Anzahl der gesichteten Vögel pro Garten deutschlandweit, in Rheinland-Pfalz, Bayern und Niedersachsen.




Verbreitungskarten / Heatmaps
[Bearbeiten]Durch Verbreitungskarten ist es möglich, eine Bestandsübersicht über Deutschland, Europa oder über einem bestimmten Gebiet vereinfacht darzustellen. Dazu können verschiedene Programme wie beispielsweise LibreOffice Impress oder andere öffentlich zugängliche Internetseiten.
Hierfür tragen die Schüler und Schülerinnen die Werte der Sichtungen in ein selbst erstelltes Raster ein, welches über dem gewählten Gebiet liegt und diese nimmt daraufhin je nach Sichtungsanzahl eine selbst erstellte Farbe an, die anzeigt, ob hier viele oder wenige Vögel dieser Art gesichtet wurden. Hier besteht die Schwierigkeit darin, die Farblegenden für jede Art so zu wählen, um ein aussagekräftiges Ergebnis zu generieren und eine farbige Karte zu erhalten.
Auf diese Weise kann die Verbreitungen der verschiedenen Arten beobachtet werden und mit denen anderer Vögel gesichtet werden. Ebenso kann hierdurch ihr Habitat bestimmt werden, wenn die Karte nur über einem Ausschnitt eines Bundeslandes liegt, also ob sie eher in städtischen Gegenden verbreitet sind oder sich in weit entfernten Waldgebieten niederlassen.
Die Schülerinnen und Schüler tragen für ein bis zwei Vögel die Werte in eine von ihnen konzipierte Deutschlandkarte ein und vergleichen die Vögel nicht nur untereinander, sonder auch den Wandel, der von 2006 bis 2022 durchlaufen wurde. Hierfür einige selbst generierte Beispielkarten:






Prozentualer Anteil an Silbermöwen in Deutschland
[Bearbeiten]Ebenso soll den Schülerinnen und Schüler verdeutlich werden, welche Rolle es spielt, wo Beobachtungen kartiert werden. Dies wird am Beispiel der Silbermöwe gezeigt. Hierbei wollen wir die erhobenen Daten unter Einbeziehung der Lebensweisen der verschiedenen Arten betrachten und deshalb geologische Standortvoraussetzungen miteinbeziehen. Außerdem wollen wir aufzeigen das es wichtig ist, kleinere Areale zu betrachten da sie oft aussagekräftiger sind. Die verwendeten Daten der Silbermöwe stammen aus den Auswertungen der Stunde der Gartenvögel 2023, die von der NABU unter Beteiligung der Bevölkerung stattgefunden hat, welche die Schülerinnen und Schüler tabellarisch zusammentragen.
Mit Hilfe der Prozentrechnung konnte klar aufgezeigt werden wo der Großteil der Silbermöwenpopulation anzutreffen ist und wo gegebenenfalls Naturschutzgebiete zum Schutz beitragen könnten. Um nun die Daten zu visualisieren, verwenden wir Säulen- und Kreisdiagrammen, um den Schülern und Schülerinnen einen anderen Zugang zu ermöglichen und die Ergebnisse verständlicher und greifbarer zu machen.
| Gesamtzahl aller gesicht. Vögel 2023 | Absoluter Anteil Silbermöwen | % Anteil aller Silbermöwensichtungen | |
|---|---|---|---|
| Deutschland | 1294024 | 778 | 0,0601 |
| Bremen | 8488 | 26 | 0,3063 |
| Hamburg | 18006 | 76 | 0,4222 |
| Schleswig Holstein | 61563 | 313 | 0,5084 |
| Meck. Pom. | 35414 | 185 | 0,5224 |
| Niedersachsen | 144613 | 69 | 0,0477 |
| 5 Bundesländer in Meeresnähe | 268084 | 669 | 0,2495 |
| 11 restl. Bundesländer | 1025940 | 109 | 0,01062 |
→85,98971 % der Sichtungen in Meeresnähe


Den Kindern wird so bewusst gemacht, dass geologische Faktoren große Auswirkungen auf die Beobachtungsdaten und somit Bestandsdaten haben und immer mit einbezogen werden müssen. Außerdem wird deutlich, dass es oft nicht sinnvoll ist zu große Verbreitungsgebiete zu betrachten, da die Diversität der Lebensräume viel zu hoch ist. In den Diagrammen ist deutlich zu erkennen welche Rolle allein die Meeresnähe bei der Verbreitung der Silbermöwe spielt, wobei diese keine Erklärung für die Daten von Niedersachsen liefert. Dies hält Raum offen für eine Diskussionsgrundlage über mögliche Ursachen, Zusammenhänge und Folgen.
Bewertung und Optimierung
[Bearbeiten]Die mathematische Theorie zur Modellierung von Vogelarten kann bereits ab Klasse 7 problemlos eingeführt werden und kann sogar ab Klasse 5 in vereinfachter Form vermittelt werden. Je nach Klassenstufe kann die Theorie angepasst werden, um den Schülerinnen und Schülern gerecht zu werden. Ein zentrales Konzept, das in jeder Klasse eingeführt werden kann, ist das Gesetz der großen Zahlen.
Bei der Modellierung gibt es einige wichtige Aspekte zu beachten. Die Zuordnung von Vogelarten mit bloßem Auge ist herausfordernd und die gezählten Sichtungen der Schülerinnen und Schüler können von verschiedenen Faktoren wie z.B. Wiederholungszählungen, Doppelzählungen, Falschzählungen, Dauer, Uhrzeit, Jahreszeit, Wetterverhältnisse, Nahrungsstandorte und Standorte allgemein beeinflusst werden. Daher wird das Gesetz der großen Zahlen betont, um die Bedeutung von ausreichend vielen Datenpunkten zu verdeutlichen.
Ein positiver Aspekt ist, dass bereits viele Daten zur Zählung bestimmter Gartenvögel in den letzten 17 Jahren vorliegen. Dennoch bleibt die Genauigkeit aufgrund verschiedener Einflussfaktoren begrenzt. Dies ermöglicht es den Schülerinnen und Schülern, die Realität von Daten zu erkennen und angemessene Erwartungen zu entwickeln.
Die Erstellung von Verbreitungskarten kann an die Schülerinnen und Schülern angepasst werden und ist daher für Modellierenden von der 5. bis zur 10. Klasse geeignet. Dies macht die Aufgabe interaktiv und unterhaltsam. Es ist jedoch wichtig, dass die gewählten Regionen angemessen sind, um eine genaue Darstellung zu ermöglichen.
Bei der Untersuchung des prozentualen Anteils an Silbermöwen in Deutschland sollte ein kleineres Raster verwendet werden, da Bundesländer zu groß sind. Es ist auch wichtig, mehrere Merkmale zu betrachten, die den Lebensraum von Silbermöwen beeinflussen, anstatt sich ausschließlich auf die Meeresnähe zu konzentrieren.
Insgesamt ermöglicht die mathematische Theorie und Modellierung den Schülerinnen und Schülern, komplexe Themen zu erforschen und die Herausforderungen bei der Datenerfassung und -interpretation zu erkennen, um ein besseres Verständnis für die Realität von Daten zu entwickeln.
Um die Ergebnisse zu Optimieren müssten die Zählungen unter exakt gleichen Bedingungen stattfinden. Zudem sollte die Stichprobe erweitert werden. Zum Erweitern könnte eine sehr viel größere Gruppe an Schüler und Schülerinnen gewählt werden, der Zeitraum der Zählung verlängert werden oder ein fester Standort der Zählungen ausgewählt werden. Damit Arten relativ eindeutig bestimmt werden, könnten Bilder der Vögel, Stimmaufnahmen oder Videoaufnahmen zugezogen werden, was wir später in Form eines Algorithmus in Sek II verbessern möchten. Um Aussagen über die Entwicklung der Artenzahlen zu treffen ist dieser Modellierungszyklus noch zu ungenau. Daher wird die Prognose für die Zukunft anhand von genaueren Daten in Modellierungszyklus 2 umgesetzt.
Software
[Bearbeiten]- Tabellenkalkulation LibreOffice Calc
- GeoGebra
Modellierungszyklus 2- Niveau Sekundarstufe 2
[Bearbeiten]Einführung
[Bearbeiten]In der Sekundarstufe II streben wir danach, zusätzliche Verfahren einzuführen, um die Zählungsdaten auf neue Weise darzustellen und beispielsweise Prognosen für die Zukunft zu erstellen. Durch die Anwendung weiterer Verfahren eröffnen sich uns neue Möglichkeiten, die gesammelten Zählungsdaten zu analysieren und zu interpretieren. Wir streben danach, über die bloße Erfassung von Zahlen hinauszugehen und ein tieferes Verständnis für die zugrunde liegenden Muster und Zusammenhänge zu gewinnen.
Ein wichtiger Aspekt bei der Analyse der Zählungsdaten ist die Fehlerfunktion. Sie ermöglicht es uns, Abweichungen zwischen den tatsächlichen Daten und den prognostizierten Werten zu quantifizieren. Indem wir die Fehlerfunktion nutzen, können wir die Genauigkeit unserer Prognosen bewerten und gegebenenfalls Anpassungen vornehmen, um präzisere Vorhersagen für die Zukunft zu treffen und ein höheres Niveau der Datenanalyse zu erreichen.
Um ein höheres Niveau in unseren Vogelzählungen zu erreichen, ist es notwendig, die Sichtungen mit dem bloßem Auge zu überwinden, da diese zu ungenau sind. Wir streben danach, Fehler zu minimieren, indem wir präziser arbeiten. Deshalb müssen wir uns die Grundlagen zur Errichtung eines Algorithmus erarbeiten. Denn durch die Entwicklung eines Algorithmus als Grundlage wollen wir Zählungsfehler wie Doppelzählungen, Falschzählungen und wiederholte Zählungen minimieren.
Darüber hinaus ermöglicht uns der Einsatz eines Algorithmus, verschiedene Einflussfaktoren wie den Standort und Umwelteinflüsse einzubeziehen, um das Ergebnis präziser zu gestalten. Indem wir Konfidenzintervalle in den Algorithmus integrieren, können wir auch erkennen, welche Fehler bei den Zählungen auftreten und wie diese behoben werden können. Dieses Vorgehen hilft uns, die Genauigkeit unserer Zählungen zu verbessern.
Mathematische Theorie
[Bearbeiten]Differenzenfolgen
Eine Differenzenfolge ist eine spezielle Art von mathematischer Folge, bei der die aufeinanderfolgenden Glieder durch Differenzbildung gebildet werden. Sie entsteht durch Subtraktion aufeinanderfolgender Glieder einer gegebenen Ausgangsfolge.
Differenzenfolgen spielen eine wichtige Rolle bei der Vermittlung eines tieferen Verständnisses mathematischer Reihen und Funktionen an Schülerinnen und Schüler. Durch die Analyse von Mustern und Regelmäßigkeiten in Differenzenfolgen können sie die Struktur von Funktionen besser erkennen. Zudem ermöglichen Differenzenfolgen die Untersuchung von Funktionen hinsichtlich ihrer Steigung oder Änderungsrate. Die Nährungsmethode wird verwendet, um Ableitungen von Funktionen zu approximieren. Dadurch gewinnen Schülerinnen und Schüler ein tieferes Verständnis für mathematische Konzepte und deren Anwendung.
Fehlerfunktion
Die Fehlerfunktion ist eine mathematische Funktion, die verwendet wird, um die Abweichung zwischen einem tatsächlichen Wert und einem erwarteten Wert zu quantifizieren. Sie findet Anwendung in der Statistik und Wahrscheinlichkeitstheorie. Sie ermöglicht die Bewertung von Messfehlern, die Berechnung von Wahrscheinlichkeiten und die Fehleranalyse. Die Fehlerfunktion wird oft mit der Normalverteilung in Verbindung gebracht und liefert Werte zwischen -1 und 1.
Bedingte Wahrscheinlichkeit
In der Sekundarstufe II wird die bedingte Wahrscheinlichkeit als Teil der Wahrscheinlichkeitstheorie behandelt. Dabei geht es um die Berechnung der Wahrscheinlichkeit eines Ereignisses unter der Bedingung, dass ein anderes Ereignis bereits eingetreten ist. Schülerinnen und Schüler lernen, wie man die bedingte Wahrscheinlichkeit berechnet und anwendet, bei mehrstufigen Zufallsexperimenten. Die bedingte Wahrscheinlichkeit ist ein wichtiger Bestandteil der Statistik und hilft dabei, Wahrscheinlichkeiten in komplexeren Situationen zu bestimmen.
- Definition: sind A,B∈F Ereignisse mitP(B)>0, so heißt P(A∣B)∶= P(A∩B)/P(B) die bedingte Wahrscheinlichkeit für (das Eintreten von) A unter der Bedingung B.[11]
Gesetz der großen Zahlen
Im fortgeschrittenen Mathematikunterricht der Sekundarstufe II werden Schülerinnen und Schüler häufig mit dem Gesetz der großen Zahlen konfrontiert. Dieses Konzept wird anhand von konkreten Beispielen und mathematischen Beweisen vermittelt. Dabei lernen die Schülerinnen und Schüler, wie sie das Gesetz der großen Zahlen auf reale Situationen anwenden können. Zudem wird der Zusammenhang zu anderen stochastischen Konzepten wie der Varianz und dem zentralen Grenzwertsatz herausgestellt. Durch dieses Verständnis erlangen die Schülerinnen und Schüler die Fähigkeit, statistische Aussagen zu treffen und Vorhersagen basierend auf großen Stichproben zu machen.
Konfidenzintervalle
Konfidenzintervalle sind statistische Maße, die einen Bereich um einen geschätzten Parameter angeben, innerhalb dessen der wahre Wert mit einer bestimmten Wahrscheinlichkeit liegt. Sie berücksichtigen Unsicherheiten bei Schätzungen und helfen, die Genauigkeit von Ergebnissen zu quantifizieren. Die Intervalle werden basierend auf statistischen Methoden und Annahmen über die Verteilung der Daten berechnet und dienen dazu, Unsicherheiten zu berücksichtigen und verlässlichere Aussagen zu machen.
Dabei wird der Anteil festgelegt, mit welcher Wahrscheinlichkeit man das Intervall treffen möchte (z.B mit 97,5%) und mit der unten genannten Formel wird Ober- und Untergrenze des Intervalls berechnet. Diese liegen dicht beieinander, wenn es viele Werte (z.B. Vogelbeobachtungen) gibt und die Grenzen verschieben sich voneinander, wenn es weniger Werte gibt oder die Wahrscheinlichkeit, mit der das zu Sehende eintrifft, verringert.
Bezug zum Rahmenlehrplan
[Bearbeiten]Eingeordnet wird in den Rahmenlehrplan der Sekundarstufe II von Rheinland-pfalz im Fach Mathematik aus dem Jahr 2015.
- L2 Messen: Konfidenzintervalle und Fehlerfunktion
--> 2.06g Lage- und Streumaße einer Stichprobe bestimmen und deuten --> 2.07g Erwartungswert und Standardabweichung diskreter Zufallsgrößen bestimmen und deuten
- L5 Daten und Zufall: bedingte Wahrscheinlichkeit
--> 5.03g Teilvorgänge mehrstufiger Zufallsexperimente auf stochastische Unabhängigkeit anhand einfacher Beispiele
untersuchen
Modellierung
[Bearbeiten]Differenzenfolge
[Bearbeiten]Zur Berechnung der Differenzfolge wurden die zuvor bereits verwendeten Werte der "Stunde der Gartenvögel" verwendet. Um die werte der Differenzenfolge zu erhalten, wurde immer die Differenz der Werte zweier aufeinanderfolgenden Jahren gebildet. Die Formel lautet: mit n= Jahr und = Anzahl des Vogels pro Garten im Jahr n. Die erhaltene Differenzenfolge wurde dann in Geogebra eingetragen. Im Anschluss können die Schüler und Schülerinnen durch ausprobieren mit Hilfe der Schieberegler in Geogebra versuchen eine Funktion zu finden die möglichst viele Werte der Differenzenfolge enthalten.
Ziel ist es, dass die Schüler und Schülerinnen mögliche Muster und Regelmäßigkeit der Differenzenfolge erkennen und mit Hilfe des Graphen so auch eine Prognose für die Zukunft aufstellen können. Durch einfaches ablesen des Graphen können die Schüler und Schülerinnen vermuten wie viele Vögel es in 5, 10 oder 20 Jahren geben könnte.
Daten Haussperling
| Jahr | Anzahl Haussperling pro Garten (deutschlandweit) | Differenzenfolgen |
|---|---|---|
| 2006 | 5,03 | |
| 2007 | 5,23 | 0,2 |
| 2008 | 5,11 | -0,12 |
| 2009 | 5,03 | -0,08 |
| 2010 | 4,74 | -0,29 |
| 2011 | 5,3 | 0,56 |
| 2012 | 5,34 | 0,04 |
| 2013 | 5,63 | 0,29 |
| 2014 | 5,68 | 0,05 |
| 2015 | 4,86 | -0,82 |
| 2016 | 4,78 | -0,08 |
| 2017 | 4,82 | 0,04 |
| 2018 | 4,93 | 0,11 |
| 2019 | 5,24 | 0,31 |
| 2020 | 4,95 | -0,29 |
| 2021 | 5,46 | 0,51 |
| 2022 | 5,52 | 0,06 |



Fehlerfunktion
[Bearbeiten]Die obigen beiden graphischen Abbildungen zeigen jeweils die Fehlerfunktion von Haussperling und Amsel deutschlandweit pro Garten von 2006 bis 2022. Die Funktion kann nur annährungsweise bestimmt werden. Dazu wurde zuerst eine Funktion gesucht die ungefähr dem Verlauf der Punkte entspricht und schließlich mit verschiedenen Parameter angepasst. Dies wird herausgefunden indem man mit Schiebereglern auf Geogebra probiert, welche Funktion bestmöglich zu den Punkten passt.
Da die Funktion trotzdem nicht jeden einzelnen Punkt mit einbezieht muss die Fehlerfunktion berechnet werden. Eine Fehlerfunktion ist eine mathematische Funktion, die den Abstand oder die Differenz zwischen den tatsächlichen Werten x und den vorhergesagten Werten y in einem Modell quantifiziert. Sie kann als f(y, y1) dargestellt werden. Da es sich bei dem Modell um eine Regressionsaufgabe handelt, muss der mittlere quadratische Fehler (MSE) ausgerechnet werden. Die Formel lautet:
f(y,y1) = (1/n) * Σ(y - y1)^2
wobei n die Anzahl der Datenpunkte ist, y die tatsächlichen Werte und y1 die vorhergesagten Werte sind. Der MSE berechnet den durchschnittlichen quadratischen Unterschied zwischen den tatsächlichen und den vorhergesagten Werten und gibt eine quantitative Messung des Fehlers im Modell. Je kleiner der MSE, desto besser passt das Modell zu den Daten.
Setzen wir die oben genannten Werte in unsere Formel ein, erhalten wir einen MSE von gerundet 0,000718.
Die Vorteile der MSE liegen darin, dass sie alle Fehler berücksichtigt und positive sowie negative Abweichungen gleich behandelt. Durch das Quadrieren der Differenzen werden größere Fehler stärker gewichtet, was dazu führen kann, dass das Modell stärker auf Ausreißer reagiert. Die MSE kann auch dazu verwendet werden, um verschiedene Modelle miteinander zu vergleichen und das Modell mit den geringsten Fehler auszuwählen.
Prognose für die Zukunft
[Bearbeiten]Aus den Differenzenfolgen alleine lässt sich keine Prognose für die Zukunft erstellen. Jedoch helfen uns diese Muster und Regelmäßigkeiten zu erkennen und somit mathematische Reihen zu identifizieren und analysieren. Aus diesem Grund können gewisse Trends oder auch Veränderungen erkannt werden, die auf die spätere Entwickelung hindeuten können. Um eine realistische Prognose aufzustellen zu können fehlen weitere Informationen über Einflussfaktoren wie z.B. Klimawandel, politische Aspekte, Naturschutzgebiete, Insektensterben, etc.
Dafür können z.B. Zeitreihenanalysen zugezogen werden. Zeitreihenanalyse ist eine statistische Technik, die verwendet wird, um Daten zu analysieren, die über eine aufeinanderfolgende Reihe von Zeitpunkten gesammelt wurden. Diese Methode geht davon aus, dass es eine Abhängigkeit zwischen den vergangenen, gegenwärtigen und zukünftigen Werten der Daten gibt. Ziel der Zeitreihenanalyse ist es, Muster, Trends und Zusammenhänge in den Daten zu identifizieren und Vorhersagen über zukünftige Werte oder Ereignisse zu treffen.
Bedingte Wahrscheinlichkeit am Beispiel der Silbermöwe
[Bearbeiten]Die bedingte Wahrscheinlichkeit am Beispiel der Silbermöwe zeigt deutlich, dass das Vorkommen dieser Vogelart an Küsten wahrscheinlicher ist als an anderen Orten. Die Meeresnähe hat einen direkten Einfluss auf das Auftreten von Silbermöwen. Durch die Analyse der bedingten Wahrscheinlichkeit gewinnen Schülerinnen und Schüler ein Verständnis für statistische Zusammenhänge und die Anwendung von Wahrscheinlichkeitstheorie. Es ermöglicht eine gezielte Vorhersage über das Auftreten der Silbermöwe an verschiedenen Standorten.

Vogelmonitoring
[Bearbeiten]Beim Vogelmonitoring können Hilfsmittel wie Wildkameras genutzt werden, um Vögel genau zu bestimmen und Doppel-, Falsch- und Wiederholungszählungen zu vermeiden. Mit speziellen Kameras kann auch die ultraviolette Musterung der Vögel erfasst werden, wodurch sie unterscheidbarer sind. Durch die Entwicklung eines Algorithmus mit Konfidenzintervallen und anderen Fehlerbehebungsmethoden können Vogelarten identifiziert und gezählt werden. Vogelmonitoring ermöglicht eine genauere Erfassung von Vogelarten und liefert wichtige Informationen für Naturschutz und Forschung. Es bezieht sich auf die systematische Beobachtung von Vogelpopulationen, um Veränderungen in ihrer Verbreitung und Bestandsentwicklung zu erfassen.
Items für einen Algorithmus[13] sind die grundlegenden Elemente oder Datenelemente, die vom Algorithmus verarbeitet oder manipuliert werden. Je nach Art des Algorithmus können Items verschiedene Formen haben, wie der Standort oder morphologische Merkmale. Folgende Items könnten beispielhaft für den Algorithmus dienen:
- Größe des Vogels (<Spatz, Amsel, Taube, >Taube)
- Habitat ([Küste, Meer, Strand], [Süßwasser, Sümpfe], [Heide, Gebüsch], [Wiese, Felder], [Wald], [Gebirge], [Städte, Dörfer, Gärten, Parks])
- Schnabellänge (kurz, mittel, lang)
- Schnabelform (konisch, überkreuzt, gebogen, länglich, entenschnabelförmig, Haken)
- Fußfarbe (pale, dunkel, grün, orange, rosa oder rötlich, gelb)
- Flügelbinde (Hat Flügel eine Musterung/andere Farbe?)
- Schwanzlänge (kurz, mittel, lang)
- Schnabelfarbe (pale, dunkel, grün, rosa, rot, gelb)
- Kopfplattenfarbe (schwarz, weiß, grau, blau, braun, rot, grün, gelb)
- Rückenfarbe (weiß, schwarz, grau oder dunkelbraun, hellgrau oder hellbraun, blau, rosa oder rötlich, grün orange, gelb, gesprenkelt oder gestreift)
- Farbe Unterseite/Bauch (schwarz, weiß, grau oder dunkelbraun, hellgrau oder hellbraun, blau, rosa oder rötlich, grün orange, gelb)
- Muster Unterseite/Bauch (uniform, quergestreift, gesprenkelt oder gepunktet)
semantisches Netz
[Bearbeiten]Zum Schreiben eines Algorithmus kann ein semantisches Netz helfen. Ein semantisches Netz ist eine visuell ansprechende Darstellung, die verwendet wird, um Wissen und Bedeutung in einer vernetzten Struktur zu repräsentieren. Es besteht aus Begriffen, die durch Matritzen miteinander verknüpft sind. Sie finden Anwendung in verschiedenen Bereichen wie künstlicher Intelligenz, Informationsverarbeitung und Wissensmanagement. Durch ihre Fähigkeit, Beziehungen und Zusammenhänge zu modellieren, unterstützen semantische Netze das Verständnis, die Suche und die Verarbeitung von Informationen. Hierbei wird die Reihenfolge festgelegt, in welchem die Vögel gescannt werden, in welche Raster das Bild oder Video aufgeteilt wird und welche Merkmale / Items mehr zählen als andere.
Hierfür dienen gewichtete Graphen. Mit ihnen werden einzelnen Merkmalen eine höhere Bedeutung beigemessen und zählen mehr bei der Bestimmung des Vogels als andere Merkmale. So zählt beispielsweise ist die Kopfkappenfarbe in der Regel sehr charakteristisch für einen Vogel und spielt eine größere Rolle beim Scannen des Vogels als die Beinlänge des Vogels. Ebenso werden schon die Fehlerbehebungsmethoden eingebaut, die im Zweifel nach einer bestimmten Logik entscheiden.
Wie beispielsweise bei der Unterscheidung von Blaumeise und Kohlmeise: Die zwei Vogelarten sehen nahezu gleich aus und sind sehr schlecht zu unterscheiden aus großer Entfernung. Die Fehlerbehebung könnte hierbei so aussehen, dass der Algorithmus das Habitat der Beobachtung kennt und dann nach Wahrscheinlichkeiten des Auftretens in diesem Gebiet auf eine der Meisen schließt. Ebenso könnte der Blauanteil in einzelnen Rastern gemessen werden und wenn der Anteil über x% liegt, so ist es eine Blaumeise.
Basierend auf diesen Ideen werden die Schülerinnen und Schüler nun ein semantisches Netz für das Monitoring der Vögel erarbeiten, um beispielsweise Vögel besser zu unterscheiden. Hierbei prüfen Sie die Items nach Relevanz, welche Sie durch Anwendung des Algorithmus an verschiedenen Vögeln überprüfen, wie beispielsweise an Meisen (unten). Durch die Konfidenzintervalle, der Fasilogik bzw. den Rastererkennungsmöglichkeiten wird ermittelt, zu wieviel % es eine bestimmte Meisenart sein kann.

Konfidenzintervalle
[Bearbeiten]Konfidenzintervall ist ein Begriff in der Statistik, der beschreibt, wie sicher man sich sein kann, dass ein sich aus mehreren Messungen ergebender Mittelwert dem wahren Mittelwert entspricht. Das bedeutet, wenn nur eine kleine Gruppe von Menschen in einem kleinen Gebiet einen bestimmten Vogel zählt, dann ist der errechnete Mittelwert sehr ungenau, da die Streuung sehr groß ist. So ist auch das Konfidenzintervall dementsprechend groß, da die Wahrscheinlichkeit, dass dies der tatsächliche Mittelwert ist, sehr gering ist.
Wenn im Gegenzug sehr viele Menschen in ganz Deutschland diesen Vogel zählen, ist der Mittelwert dieser Zählungen sehr genau und repräsentativ, da die Streuung auch nur sehr gering ist und es verlässlichere Werte gibt. Somit ist das Konfidenzintervall sehr klein, da die Wahrscheinlichkeit, dass der Mittelwert in diesem Bereich liegt, sehr groß ist. (siehe Abb.)
Dies machen sich Forscher und Forscherinnen zu Nutze und versuchen immer große Stichproben zu erlangen, wie auch der Naturschutzbund in Deutschland (NABU) und mit dieser Methoden sollen auch die Oberstufenschüler und -schülerinnen arbeiten und in den Algorithmus einbauen.

Berechnung des Konfidenzintervalls des Haussperlings 2010: Wir wählen das Konfidenzniveau von 95% bei einer Stichprobengröße von N=96 Landkreise. Damit ergeben sich folgende Intervallober- und untergrenzen
Berechnung des Konfidenzintervalls des Haussperlings 2020: Wir wählen das Konfidenzniveau von 95% bei einer Stichprobengröße von N=96 Landkreise. Damit ergeben sich folgende Intervallober- und untergrenzen
Bewertung und Optimierung
[Bearbeiten]Die Verwendung von Differenzenfolgen und Fehlerfunktionen bietet verschiedene Möglichkeiten, mathematische Konzepte zu veranschaulichen. Allerdings sind sie nicht immer genau oder für unser spezifisches Beispiel präzise anwendbar, da individuelle Anpassungen der Regler in Geogebra zu Ungenauigkeiten führen können. Die bedingte Wahrscheinlichkeit in unserem Fallbeispiel bezieht sich nur auf einen spezifischen Einflussfaktor und ist auf eine bestimmte Art der Anwendung beschränkt. Es ist wichtig zu beachten, dass nicht alle Einflussfaktoren für jede Situation bekannt sind, was die umfassende Analyse erschwert. Das Schreiben eines Algorithmus kann eine hohe Anforderung darstellen und ist möglicherweise für Schülerinnen und Schüler zu anspruchsvoll. Zudem gestaltet sich die Fehlerbehebung oft ungenau, da es schwer vorherzusagen ist, welche Art von Fehlern auftreten können.
Die Einführung von Matrizen und gewichteten Graphen sind komplexe Themen, die möglicherweise erst in fortgeschrittenen Kursen behandelt werden sollten, da sie für eine grundlegende Einführung zu komplex sind. Auf der anderen Seite verdeutlichen Konfidenzintervalle die Bedeutung des Gesetzes der großen Zahlen und zeigen, warum es wichtig ist, große Zahlen in unserer Auswertung zu berücksichtigen.
- Differenzenfolge und Fehlerfunktion gut für mehr Darstellungsformen aber nicht zielführend und sehr ungenau weil Regler auf Geogebra individuell verstellt werden können
- kann nur bespielhaft dargestellt werden und nicht präzise für unser beispiel ausgerechnet werden
- bedingte wahrscheinlichkeit nur auf einen einflussfaktor bezogen und nur auf eine art angewandet
- nicht alle einflussfaktoren bekannt für jede art
- Algorithmus schreiben sehr schwer und überfordert schüler und schülerinnen, fehlerbehebungsmethoden zu ungenau und ungewiss welche fehler auftauchen
- gewichtete Graphen sehr komplex
- matrizen können damit nicht eingeführt werden weil zu komplex nur für fortführung geegnet
- konfidenzintervalle verdeutlichen warum gesetz der große zahlen wichtig ist
- große zahlen relevant für unsere auswertung
Software
[Bearbeiten]- Tabellenkalkulation OfficeLibre Calc
- GeoGebra
Modellierungszyklus 3- Niveau Universität
[Bearbeiten]Einführung
[Bearbeiten]In diesem Modellierungszyklus nutzen wir weitere Darstellungsformen um die Verbreitung von Vogelarten zu visualisieren, indem wir Heatmaps oder Verbreitungskarten nutzen. Diese Karten stellen die dreidimensionale Dichtefunktion der Vogeldaten dar. Durch die Integration von verschiedenen Variablen wie Raum, Zeit und Vogeldichte wird eine umfassende Darstellung der Verbreitung ermöglicht. Dabei können verschiedene Aspekte berücksichtigt werden, die die Verbreitung beeinflussen. Beispielsweise können der Klimawandel, Naturschutzprogramme zur Verbesserung der Wasserqualität oder das Auftreten von invasiven Arten Auswirkungen auf die Verbreitung von Vogelarten haben.
Die Analyse der Verbreitung erfolgt durch mehrdimensionale Integration, um die Vogeldichte in verschiedenen Regionen zu beobachten. Dieses mehrdimensionale Integral ermöglicht eine umfassende Betrachtung der Verbreitungsmuster und bietet Einblicke in die Populationsdynamik der Vogelarten. Ebenso wird mit der Integration die Wahrscheinlichkeit aufgezeigt, mit der ein bestimmter Vogel an einem bestimmten Standort gesichtet wird. Die dadurch gesammelten Erkenntnisse können wiederum genutzt werden, um Algorithmen, zur Verbesserung des Vogelmonitorings, zu füttern. Damit können auch fehlerhafte Beobachtungen besser eingeschätzt und ausgeglichen werden, wodurch die Daten noch präziser werden.
Mathematische Theorie
[Bearbeiten]Dichtefunktion / dreidimensionale Heatmap
Eine Dichtefunktion ist eine mathematische Funktion, die die Verteilung von Wahrscheinlichkeiten für eine kontinuierliche Zufallsvariable beschreibt. Sie gibt an, wie sich die Wahrscheinlichkeit auf verschiedene Werte der Zufallsvariable in einem bestimmten Intervall verteilt. Die Dichtefunktion wird oft als Kurve dargestellt und muss bestimmte Eigenschaften erfüllen, wie beispielsweise eine nicht-negative Funktion zu sein und über den gesamten Definitionsbereich zu integrieren.
Das Vorkommen einer Vogelart kann räumlich variieren und ist nicht gleichmäßig über ein Gebiet verteilt. Eine Dichtefunktion ermöglicht es uns, diese räumlichen Variationen grafisch darzustellen und wichtige Informationen über die Verteilung der Vogelart zu erhalten. Durch die Verwendung einer Dichtefunktion können wir außerdem:
- die Häufigkeit und Konzentration des Vorkommens der Vogelart in verschiedenen Gebieten visuell erfassen
- Regionen identifizieren, in denen die Vogelart besonders häufig oder selten anzutreffen ist
- die Wahrscheinlichkeit bestimmen, dass eine bestimmte Anzahl von Vögeln in einem bestimmten Bereich beobachtet wird
- Vergleiche zwischen verschiedenen Standorten, Zeiträumen oder anderen Faktoren ziehen und Trends erkennen
- die Verwendung einer Dichtefunktion ermöglicht eine präzisere Darstellung des Vorkommens einer Vogelart, indem sie uns erlaubt, die räumliche Verteilung und die Wahrscheinlichkeiten in Bezug auf die Anzahl der Vögel zu berücksichtigen.
- die Dichtefunktion hilft uns zudem, Einblicke in das Verhalten und die Ökologie der Vogelart zu gewinnen und informierte Entscheidungen im Naturschutz und bei der Lebensraumplanung zu treffen
Integration der Dichtefunktion
Die Integration der Dichtefunktion ist sinnvoll, da sie uns wichtige Informationen über eine kontinuierliche Zufallsvariable liefert und dabei hilft, Wahrscheinlichkeiten zu berechnen. Durch die Integration über einen bestimmten Bereich können wir beispielsweise die Wahrscheinlichkeit bestimmen, dass die Zufallsvariable einen bestimmten Wert annimmt oder in einem bestimmten Intervall liegt.
Die Integration der Dichtefunktion beim Vogelvorkommen ermöglicht uns:
- die Berechnung der Wahrscheinlichkeit des Vogelvorkommens in bestimmten Gebieten
- den Vergleich von Wahrscheinlichkeiten zwischen verschiedenen Regionen
- die Ermittlung des durchschnittlichen Vogelvorkommens
- die Identifizierung von Ausreißern oder ungewöhnlichen Vorkommnissen
Vorstellung der App "NABU Vogelapp"
[Bearbeiten]Die NABU Vogel-App ist eine mobile Anwendung, die vom Naturschutzbund Deutschland (NABU) entwickelt wurde. Sie bietet Vogelbegeisterten die Möglichkeit, Vögel zu erkennen, zu bestimmen und Informationen über sie zu erhalten. Die Daten erhält der Naturschutzbund von Vogelbeobachtern, die ihre Sichtungen dokumentieren. Vorallem im Rahmen der "Stunde der Gartenvögel" und "Stunde der Wintervögel" werden die Daten zusammengetragen, welche in der Anwendung für alle sichtbar sind. Die NABU Vogel-App bietet eine Vielzahl von Funktionen, die den Benutzern helfen, Vögel zu identifizieren. Dazu gehören:
- Vogelbestimmung: Die App enthält eine umfangreiche Datenbank mit Informationen über eine Vielzahl von Vogelarten. Anhand von Bildern, Beschreibungen und Klangaufnahmen können Benutzer die Vögel in ihrer Umgebung identifizieren.
- Vogelstimmen: Die App bietet auch Audioaufnahmen der Vogelstimmen, sodass Benutzer lernen können, wie sich die verschiedenen Arten anhören. Dies ist besonders nützlich, da viele Vögel anhand ihres Gesangs leichter identifiziert werden können als anhand ihres Aussehens.
- Brutzeiten: Ebenfalls wird in der App dokumentiert, wann welche Vögel brüten und ihre Nachkommen groß ziehen, sodass Benutzer auch anhand von Nestsichtungen auf eine bestimmte Vogelart schließen können.
- Sichtungen teilen: Benutzer können ihre eigenen Vogelbeobachtungen in der App teilen und Informationen über Ort, Zeit und beobachtete Vogelarten angeben. Dadurch entsteht eine gemeinschaftliche Plattform, auf der Vogelinteressierte ihre Erfahrungen austauschen können.
- Vogelverbreitung: Die Anwendung enthält außerdem Verbreitungskarten, wodurch die Verbreitung der verschiedenen Arten zu den Jahreszeiten nicht nur in Deutschland, sonder in ganz Europa ersichtlich wird.
- Vogel-Quiz: Die App bietet auch unterhaltsame Vogel-Quizze, mit denen Benutzer ihr Wissen über Vögel testen können. Dies ist eine unterhaltsame Möglichkeit, das Wissen über Vogelarten und ihre Merkmale zu vertiefen.
Die NABU Vogel-App bietet somit eine benutzerfreundliche und interaktive Plattform für Vogelbegeisterte, um ihr Wissen über Vögel zu erweitern, ihre Beobachtungen zu teilen und an der Vogelbestimmung teilzunehmen. Sie ist eine wertvolle Ressource für Naturliebhaber und unterstützt den Naturschutz, indem sie das Bewusstsein für die Vielfalt der Vogelwelt schärft und zur Dokumentation von Vogelsichtungen beiträgt.
Modellierung
[Bearbeiten]Dreidimensionale Heatmap
[Bearbeiten]- Dichtefunktion über Bayern
- Sei Ω ⊂ R ein Intervall
Eine Funktion f ∶ Ω → R heißt Dichtefunktion (oder Dichte oder Wahrscheinlichkeitsdichte) (auf Ω), falls die folgenden Bedingungen gelten:
- es gilt f(x)≥0 für alle x∈Ω.
- f ist (Lebesgue)-integrierbar mit ∫ f(x) dx = 1.
| Landkreis | Haussperling pro graten 2020 | Koordinaten im Raster |
|---|---|---|
| Aschaffenburg (Land) | 4,98 | (1,5/3,5) |
| Aschaffenburg (Stadt) | 4,66 | (1/3) |
| Mittenburg | 5,33 | (1,5/2,5) |
| Main-Spessart | 5,95 | (3/3),(3/4) |
| Bad Kissingen | 4,06 | (4/4),(4/5),(5,5/4,5) |
| Schweinfurt (Land) | 5,73 | (5/3),(6/3),(5/4) |
| Schweinfurt (Stadt) | 3,57 | (5/3,8) |
| Würzburg (Land) | 5,52 | (4/1),(4/2),(4/3) |
| Würzburg (Stadt) | 3,04 | (4/2,5) |
| Röhn-Grabfeld | 4,71 | (4/6),(5/7),(5/6),(5/5),(6/5) |
| Haßberg | 5,46 | (6/4),(6/3),(7/4),(7/3) |
| Kitzingen | 7,94 | (5/1,5),(5/2),(5/2,5) |
| Neustadt an der Aisch-Bad Windsheim | 6,7 | (5/0),(6/0),(7/0),(5/1),(6/1),(7/1),(6/2) |





Bewertung und Optimierung
[Bearbeiten]Durch die mehrdimensionale Dichtefunktion und die Integralrechnung ist es möglich, eine Heatmap viel genauer und noch übersichtlicher darzustellen, als in der Mittelstufe. Außerdem können so verschiedene Regionen genauer betrachtet werden und deren Umweltfaktoren einbezogen werden. Mithilfe der Integralrechnung sind wir ebenso in der Lage die Vogeldichte zu bestimmen und die Wahrscheinlichkeit, mit der wir diesen bestimmten Vogel in dieser Regionen sehen können. Dies ist ein großer Schritt im Vogelmonitoring und ist nur im Uniniveau möglich.
Zu Berücksichtigen ist jedoch, dass niemals die exakte Anzahl der verschiedenen Arten festgelegt werden kann oder die genaue Ursache für Änderungen der Anzahl oder der Verbreitung. Hierfür steht uns doch die Fasilogik ("unscharfe Logik") zur Verfügung, sodass wir verschiedenen Wirkungen die höchstwahrscheinliche Ursache zugrunde legen können. So beispielsweise sind seit 2011 die Artenvielfalt und die Dauer des Aufenthalts von Wasservögeln in Deutschland gestiegen. Mit der Idee der Fasilogik liegt dies mit großer Wahrscheinlichkeit an dem Klimawandel, aber vor allem auch an den verbesserten Wasserqualitäten durch Naturschutzmaßnahmen, der Einwanderung von Neuorganismen (z.B. der Dreikantmuschel), den Vogelschutzgebieten als auch an der Schaffung neuer Gewässer. Hierdurch haben wir eine grobe Einschätzung der Ursachen und können mit diesen Wahrscheinlichkeiten arbeiten.[5]
Problematisch ist es auch, wenn der Algorithmus dauerhaft mit falschen Daten gefüttert werden würde und dadurch die Wahrscheinlichkeit, mit der man auf einen Vogel in einer bestimmten Region trifft, viel zu hoch eingeschätzt wird und auch weitere Sichtungen falsch beurteilt werden von der KI.
Software
[Bearbeiten]- Tabellenkalkulation
- Maxima
- GeoGebra
- ↑ https://biooekonomie.de/service/studien-statistiken/ipbes-2019-globaler-bericht-ueber-den-zustand-der-artenvielfalt
- ↑ https://www.afro.who.int/health-topics/womens-health (Stand: 29.12.2022)
- ↑ https://www.afro.who.int/health-topics/womens-health (Stand: 29.12.2022)
- ↑ https://www.afro.who.int/health-topics/womens-health (Stand: 29.12.2022)
- ↑ a b Gerlach, B., R. Dröschmeister, T. Langgemach, K. Borkenhagen, M. Busch, M. Hauswirth, T. Heinicke, J. Kamp, J. Karthäuser, C. König, N. Markones, N. Prior, S. Trautmann, J. Wahl & C. Sudfeldt (2019): Vögel in Deutschland – Übersichten zur Bestandssituation. DDA, BfN, LAG VSW, Münster.
- ↑ Rießinger, T. (2016). Dreisatz. In: Dreisatz, Prozente und Zinsen. essentials. Springer Spektrum, Wiesbaden. https://doi.org/10.1007/978-3-658-15085-3_1
- ↑ Hock, N. (2021). Prozentrechnung. In: Förderung von diagnostischen Kompetenzen . Mathematikdidaktik im Fokus. Springer Spektrum, Wiesbaden. https://doi.org/10.1007/978-3-658-32286-1_8
- ↑ Berger, R. (1989). Prozent- und Zinsrechnen in der Hauptschule. Didaktische Analysen und empirische Ergebnisse zu Schwierigkeiten, Lösungsverfahren und Selbstkorrektur- verhalten der Schüler am Ende der Hauptschulzeit. Regensburg: Roderer Verlag.
- ↑ Berger, R. (1989). Prozent- und Zinsrechnen in der Hauptschule. Didaktische Analysen und empirische Ergebnisse zu Schwierigkeiten, Lösungsverfahren und Selbstkorrektur- verhalten der Schüler am Ende der Hauptschulzeit. Regensburg: Roderer Verlag.
- ↑ Berger, R. (1989). Prozent- und Zinsrechnen in der Hauptschule. Didaktische Analysen und empirische Ergebnisse zu Schwierigkeiten, Lösungsverfahren und Selbstkorrektur- verhalten der Schüler am Ende der Hauptschulzeit. Regensburg: Roderer Verlag.
- ↑ a b Büchter, A. & Henn, H. (2009). Elementare Stochastik: Eine Einführung in die Mathematik der Daten und des Zufalls (Mathematik für das Lehramt) (2., überarb. u. erw. Aufl. 2007). Springer.
- ↑ Ministerium für Bildung, Wissenschaft, Jugend und Kultur Rheinland-Pfalz. (2007). Rahmenlehrplan Mathematik (Klassenstufen 5 - 9/10). Mainz.
- ↑ NABU APP







![{\displaystyle {[Varianz]}={1 \over n-1}\cdot {\sum _{j=1}^{n}(x_{j}-x)^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8514e08cc2657677f97a6d6cb3970f84de1f4e5)
![{\displaystyle {[Standardabweichung]}={\sqrt {[Varianz]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12fb69f9b50a43de2ff5a9b696099dcc936b12ab)



