Kurs:Funktionalanalysis/Cauchy-Folgen
Einführung
[Bearbeiten]Eine Cauchy-Folge ist in der Mathematik eine Folge, bei der der Abstand der Folgenglieder im Verlauf der Folge beliebig klein wird.
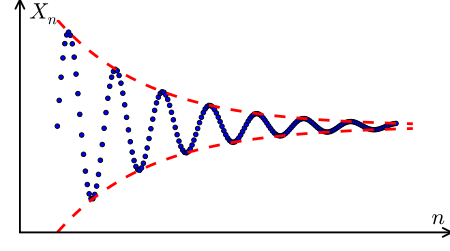
Abbildung 1 - Cauchy-Folge
[Bearbeiten]Abbildung 2 - Keine Cauchy-Folge
[Bearbeiten]Beispiel einer Folge, die keine Cauchy-Folge ist: der Abstand der Folgenglieder wird im Verlauf der Folge nicht beliebig klein.
Geschichte
[Bearbeiten]Cauchy-Folgen sind nach dem französischen Mathematiker Augustin-Louis Cauchy benannt und von grundlegender Bedeutung für den Aufbau der Analysis. In dieser Lernressource wird der Begriff der Cauchy-Folge im Kontext von normierten Räumen behandelt, auf denen zusätzliche ein Multiplikation existiert.
Grenzwert einer Cauchy-Folge
[Bearbeiten]Der Grenzwert einer Cauchy-Folge reeller Zahlen ist immer eine reelle Zahl. Der Grenzwert einer Cauchy-Folge rationaler Zahlen kann auch eine irrationale Zahl sein. Allgemein konvergieren genau dann alle Cauchy-Folgen von Elementen eines metrischen Raums, falls der Raum vollständig ist. Jeder unvollständige metrische Raum kann durch die Bildung von Äquivalenzklassen von Cauchy-Folgen vervollständigt werden.
Definition Cauchy-Folgen
[Bearbeiten]Cauchy-Folgen können allgemeiner (z.B. in beliebigen metrischen Räumen) definiert werden. Zunächst betrachten wir Cauchy-Folgen in Zahlenräume.
Definition - Cauchy-Folge von Zahlen
[Bearbeiten]Eine Folge rationaler oder reeller Zahlen heißt Cauchy-Folge oder Fundamentalfolge, wenn es zu jedem einen Index gibt, so dass ab diesem Index alle Folgenglieder weniger als voneinander entfernt sind. Formal lässt sich diese Bedingung als
schreiben, wobei den Betrag einer Zahl darstellt.
Anmerkungen
[Bearbeiten]- In der Definition kann auch durch und auch durch ersetzt werden.
- Äquivalent zu dieser Definition kann man auch fordern, dass es zu jeder noch so kleinen positiven Zahl ein Intervall der Länge gibt, in dem fast alle Folgenglieder liegen.
- Diese Definition entspricht weitgehend der Definition für konvergente Folgen, ohne jedoch den Begriff des Grenzwertes einer Folge zu benutzen. Cauchy-Folgen wurden daher früher auch als „in sich konvergente Folgen“ oder „konzentrierte Folgen“ bezeichnet.
Beispiel 1 - Cauchy-Folge
[Bearbeiten]Die Folge ist eine Cauchy-Folge. Man kann nämlich zu einem beliebig vorgegebenen ein so wählen, dass erfüllt ist. Sind nun beliebig gewählt, dann gilt
- .
Beispiel 2 - Keine Cauchy-Folge
[Bearbeiten]Die Folge ist keine Cauchy-Folge. Sei dazu gewählt und eine beliebige natürliche Zahl. Dann kann man und wählen und es gilt immer[1]
- .
Vollständigkeit und rationale Zahlen
[Bearbeiten]Wir betrachten die Menge der rationalen Zahlen und erzeugen eine Cauchy-Folge in , die ein Cauchy-Folge in ist, aber keinen Grenzwert in besitzt.
Konstruktion der Cauchy-Folge
[Bearbeiten]Um eine solche Cauchy-Folge in den rationalen Zahlen zu erzeugen, nimmt man einen Startwert . Die weiteren Folgenglieder werden induktiv durch innere Verknüpfungen in dem Körper gebildet.
- .
Heron-Verfahren
[Bearbeiten]In diesem Beispiel wird also die Folge rationaler Zahlen Heron-Verfahren generiert, das für beliebige eine Folge generiert, die allgemein mit gegen konvergiert.
- .
Irrationale Zahlen
[Bearbeiten]Ist eine irrationale Zahl (wie z.B. , so konvergiert die Folge nicht in . Die Konvergenz gegen für ist dabei unabhängig von Startwert. Dieser kann beliebig für gewählt werden.
Aufgabe - Konvergenz Heron-Verfahren
[Bearbeiten]Gegen welchen Grenzwert konvergiert das Heron-Verfahren, wenn gewählt wird? Beweisen Sie die Aussage.
Grenzwert der Folge
[Bearbeiten]Diese Folge ist eine Cauchy-Folge, sie besitzt aber als Grenzwert die irrationale Zahl und konvergiert daher innerhalb der Menge der rationalen Zahlen nicht.
Vollständigkeit
[Bearbeiten]Die Problematik der Vollständigkeit, dass in der Menge der rationalen Zahlen viele Grenzwerte von Cauchy-Folgen nicht enthalten sind, führte zu der Idee der Vervollständigung des Zahlenbereichs auf die Menge der reellen Zahlen.
Cauchy-Folgen in normierten Räumen
[Bearbeiten]In normierten Räumen übernimmt ein Norm die Aufgabe des Betrages in Zahlenräumen.
Definition - Cauchy-Folge in normierten Räumen
[Bearbeiten]Spezieller definiert man den Begriff der Cauchy-Folge für normierten Räume , also beliebige Mengen , auf denen eine Norm gegeben ist. Eine Folge von Elementen in heißt dann Cauchy-Folge in , wenn
Bemerkung
[Bearbeiten]Dies ist ein Spezialfall der Cauchy-Folge in metrischen Räumen, denn jeder normierte Raum ist mit folgender Metrik auch ein metrischer Raum :
Cauchy-Folgen in metrischen Räumen
[Bearbeiten]In metrischen Räumen gibt es ein Metrik , die im Vergleich zum Betrag , den Abstand zwischen zwei Elementen aus dem Grundraum messen kann. Dabei entspricht in Zahlenräumen .
Definition - Cauchy-Folge in metrischen Räumen
[Bearbeiten]Allgemeiner definiert man den Begriff der Cauchy-Folge für metrische Räume , also beliebige Mengen , auf denen eine Metrik gegeben ist. Eine Folge von Elementen in heißt dann Cauchy-Folge, wenn
gilt.[2]
Bemerkung - Cauchy-Folgen in metrischen Räumen
[Bearbeiten]Damit gibt es zu jedem reellen einen Index , so dass für alle natürlichen Zahlen der Abstand der entsprechenden Folgenglieder ist.
Äquivalente Formulierung
[Bearbeiten]Eine dazu äquivalente geometrische Formulierung ist: Für jedes gibt es einen Punkt und einen Index , so dass alle Folgenglieder ab in der offenen Kugel um den Punkt mit Radius liegen. Diese Version unterscheidet sich nur dadurch von der Konvergenzdefinition, dass hier der Mittelpunkt vom Radius abhängen darf, während bei der Konvergenz der Grenzwert von unabhängig sein muss.
Konvergente Folge sind Cauchy-Folgen in metrischen Räumen
[Bearbeiten]Jede konvergente Folge in einem metrischen Raum ist auch eine Cauchy-Folge. Konvergiert nämlich eine Folge gegen einen Grenzwert , dann gibt es zu jedem einen Index , sodass für alle gilt. Mit der Dreiecksungleichung für metrische Räume folgt dann für alle
und die Folge ist somit eine Cauchy-Folge.
Betrachtung der Umkehrung
[Bearbeiten]Die umgekehrte Richtung muss jedoch nicht notwendigerweise wahr sein, was letztendlich zur Einführung von vollständigen Räumen führte (siehe rationale Zahlen als Teilmenge der reellen Zahlen. In einem vollständigen Raum besitzt definitionsgemäß jede Cauchy-Folge einen Grenzwert und der Begriff der konvergenten Folge fällt mit dem Begriff der Cauchy-Folge zusammen.
Vervollständigung von metrischen Räumen
[Bearbeiten]Jeder unvollständige metrische Raum kann jedoch durch die Bildung von Äquivalenzklassen von Cauchy-Folgen vervollständigt werden. Dabei werden zwei Cauchy-Folgen und von Elementen in als äquivalent angesehen, wenn
oder äquivalent dazu . Liegt der Grenzwert einer der beiden Folgen in , dann auch der der anderen, und die beiden Grenzwerte sind gleich. Die Äquivalenzklassen der Cauchy-Folgen bilden die Vervollständigung des Grundraumes .
Aufgaben für Lernende
[Bearbeiten]In den folgenden Aufgaben werden Cauchyfolgen in normierten Räumen betrachtet, die über die grundlegenden Vektorräume mit hinausgehen
Cauchy-Folgen in Funktionenräumen
[Bearbeiten]Sei die Menge der stetigen (engl. continuous) Funktionen von dem Intervall in den Körper als Wertebereich. Ferner sei die folgende Norm auf gegeben:
- Zeigen Sie, dass der folgende Funktionenraum der stetigen Funktionen mit der folgenden Norm nicht vollständig ist.
Hinweis 1: Definition der Funktionenfolge
[Bearbeiten]Verwenden Sie die folgende Funktionenfolge mit
Hinweis 2: Abschätzung der Integralnorm
[Bearbeiten]Skizzieren Sie die Funktionen und . Für den Beweis, dass eine Cauchy-Folge in ist, sollten Sie die Integralnorm nach oben gegen einen Rechteckflächeninhalt abschätzen, wobei die Höhe des Rechtecks eine obere Schranke für den maximale Funktionswert auf dem bertrachteten Intervall darstellt.
Hinweis 3: Grenzfunktion der Funktionenfolge
[Bearbeiten]Betrachten Sie ferner die folgende Abbildung und zeigen Sie, dass die Folge punktweise gegen konvergiert:
Polynom-Vektoräume mit Koeffizienten aus normierten Räumen
[Bearbeiten]Sei auf einem -Vektorraum gegeben. Wir definieren nun den Vektorraum der Polynome mit Koeffizienten aus und eine Norm Norm , die zu einem normierten Raum macht. Definieren Sie eine Cauchy-Folge von Polynomen in , die nicht konvergent ist.
Notation
[Bearbeiten]Sei ein normierter Raum.
- ist die Menge der Folgen in dem Vektorraum , bei der ab einer Indexschranke alle Folgenglieder gleich dem Nullvektor aus .
- ist die Menge der Nullfolgen in einem normierten Vektorraum .
- ist die Menge der konvergenten Folgen in einem normierten Vektorraum .
Analog kann man diese Notation auf metrische Räume mit einer Metrik übertragen.
Siehe auch
[Bearbeiten]- Übersicht über die Vektorräume aus dem Kurs
- Cauchy-Kriterium
- Cauchy-Netz
- Topologie
- Polynomalgebra
- Vollständigkeit
Literatur
[Bearbeiten]- Konrad Königsberger: Analysis 1. Springer, Berlin 2004, ISBN 3-540-41282-4
- Konrad Königsberger: Analysis 2. Springer-Verlag, Berlin/Heidelberg, 2000, ISBN 3-540-43580-8
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg-Verlag, 8. Aufl. 2006, ISBN 3-528-67224-2
Einzelnachweise und Anmerkungen
[Bearbeiten]- ↑ Um einen Gegenbeweis zu führen, muss man die Definition umkehren: .
- ↑ Dirk Werner: Funktionalanalysis. 2005, S. 2.
Seiteninformation
[Bearbeiten]Diese Lernressource können Sie als Wiki2Reveal-Foliensatz darstellen.
Wiki2Reveal
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Funktionalanalysis' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Funktionalanalysis/Cauchy-Folgen
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.
Wikipedia2Wikiversity
[Bearbeiten]Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:




































































![{\displaystyle V:={\mathcal {C}}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ba935781730b6339df9ea4dd1ed187114eb53e7)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![{\displaystyle [a,b]:=[0,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4818a69795bdfa1f35bf8a73913287c2a6fc9ea0)
![{\displaystyle {\begin{array}{rcl}f_{n}:[a,b]&\to &\mathbb {R} \\x&\mapsto &f_{n}(x)=\left\{{\begin{array}{lcl}0&{\mbox{ für }}&x\in \left[0,1-{\frac {1}{n}}\right]\\\quad n\cdot x+(1-n)&{\mbox{ für }}&x\in \left]1-{\frac {1}{n}},1\right]\\-n\cdot x+(1+n)&{\mbox{ für }}&x\in \left]1,1+{\frac {1}{n}}\right[\\0&{\mbox{ für }}&x\in \left[1+{\frac {1}{n}},2\right]\\\end{array}}\right.\\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecc597f17183732a37a0ec5129cb8bd6d441f52d)





![{\displaystyle {\begin{array}{rcl}f_{0}:[a,b]&\to &\mathbb {R} \\x&\mapsto &f_{0}(x)=\left\{{\begin{array}{lcl}0&{\mbox{ für }}&x\in \left[0,2\right]\setminus \{1\}\\1&{\mbox{ für }}&x=1\end{array}}\right.\\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f525b4296d42fa7a5a0035df7e2113f38366b17)


![{\displaystyle V[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd4d3b31c894c1fd0b63162ae4b346783b390f50)
![{\displaystyle \|\cdot \|_{V[x]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22dad4423753a93b1020c726ca31a4f9376f7920)
![{\displaystyle (V[x],\|\cdot \|_{V[x]})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3d5aa53c372b664eec9928545e17ffeaf78482e)







