Kurs:Maßtheorie auf topologischen Räumen/Prozesse und Nachhaltigkeit

Einführung

In diesem Abschnitt werden die theoretischen Grundlagen für die Beschreibung von Prozessen behandelt. Diese beziehen sich auf die Analyse der mathematischen Maßtheorie in Bezug auf Veränderungsprozesse und bestimmten Entscheidungen, über die man diese Veränderung steuern kann. Die Güte der Veränderung wird im Sinne von definierten Maßen auf topologischen Vektorräumen betrachtet, um die Nachhaltigkeit verbessern.

Funktionenfolgen

Im weiteren Verlauf des Lernressource werden die Veränderungsprozesse zunächst als Funktionenfolgen $(f_{n})_{n\in \mathbb {N} }$ betrachtet, die im Sinne von definierten Maßen $\mu :V\to \mathbb {R}$ auf topologischen Vektorräumen die Nachhaltigkeit verbessern.

Emissionen von Treibhausgasen

Wenn z.B. die $CO_{2}$-Emissionen als Ausgabewert des Maßes $\mu (f_{n})$, so versucht man diesen Wert des Maßes mit jedem Iterationsschritt zu minimieren. Ist $\mu (f_{n})<0$, so bindet man sogar mehr $CO_{2}$ (z.B. in Biomasse), als $CO_{2}$ emittiert werden. Bei Funktionfolgen entsteht eine Iterationsverfahren in der Optimierung, bei der nach Möglichkeit

$\mu (f_{n})>\mu (f_{n+1})$

gilt.

Stochastische Prozesse

Da zukünftige Effekte im Vergleich für unterschiedliche Methoden und Entscheidungsoptionen für die Anwendungvon nicht deterministisch vorhergesagt werden können, kann man bei Funktionenfolgen zu stochastischen Prozessen übergehen, um auch die stochastische Modellbildung in den maßtheoretischen Ansatz zu intergrieren.

Aufgabe für Studierende

• Vergleichen Sie verschiedene Ansätze für die Beschreibung von Prozessen und dem Messen von Nachhaltigkeit und identifizieren Sie Vor- und Nachteile dieser Ansätze bzgl. verwendeten mathematischen Theorie.
• Betrachten Sie die Konvexkombination von Funktionen erläutern Sie, wie man von einer diskreten Beschreibung von Veränderung auf dem Funktionenraum auf eine kontinuierliche Veränderung (z.B. mit $t\in T:=\mathbb {R}$) in der Zeitmenge $T$ wechseln kann.

Stetige Transformation von Funktionen

Die folgende Animation zeigt stetige Transformation von einer $f$ in eine Funktion $g$ über Konvexkombinationen. Diese Transformation besitzt eine nicht-diskreten Zeitmenge $T:=[0.1]$ im Gegensatz zu einer diskreten Zeitmenge $T:=\mathbb {N}$ aus den obigen Beispielen. Der rote Graph beschreibt die Konvexkombination $f_{t}:=K(t)$ im Funktionenraum und zeitlicher Interpretation die Funktion $f_{t}$ zum Zeitpunkt $t$.

Animation - Transformation von Funktionen

Konvexkombination von zwei Funktionen in Geogebra

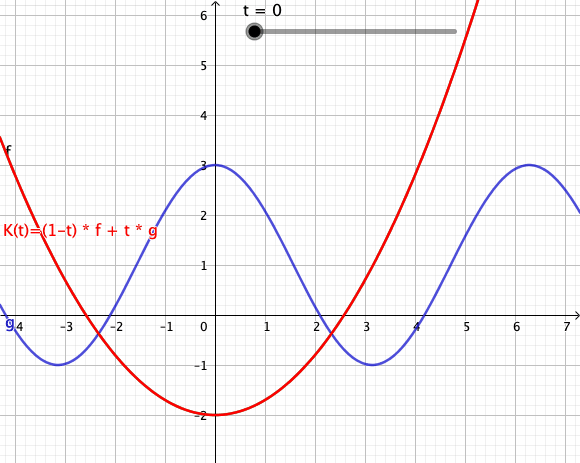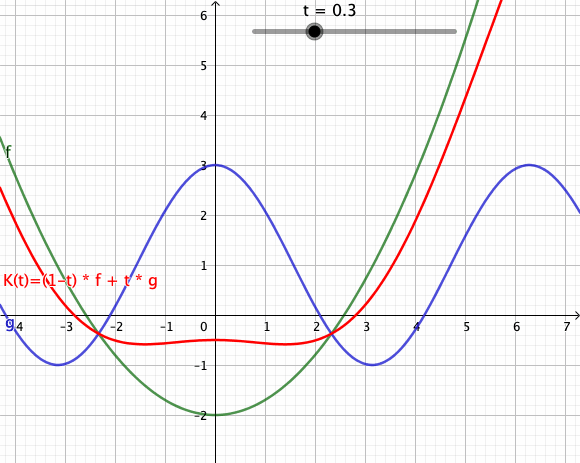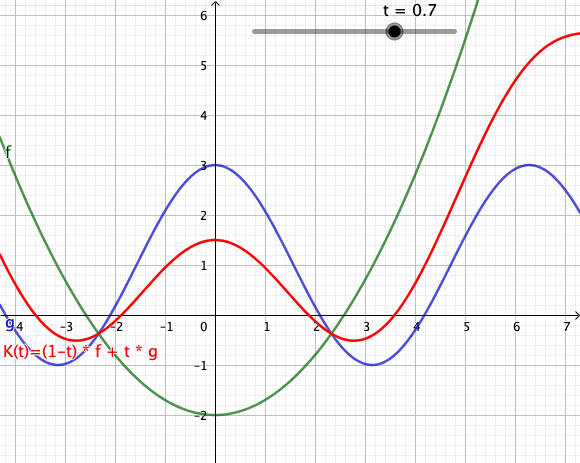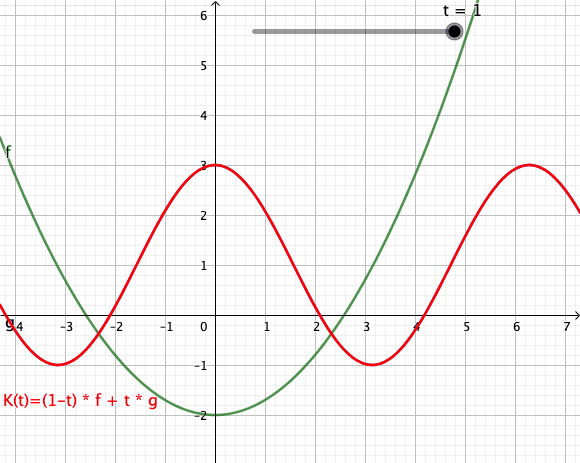
Geogebra: Interaktives Applet - Download: Geogebra-File

Verbesserung und Verschlechterung im Definitionsbereich

Betrachtet man den Funktionswert $f(x)$ an eine Dichtefunktion, bei der positive Werte eine Emission von $CO_{2}$ und ein negative Werte ein Binden von $CO_{2}$ in Holz durch Fotosynthese veranschaulicht.

• An einigen Stellen auf der x-Achse verbessert sich die Situation,
• An einigen Stellen auf der x-Achse verschlechtert sich die Situation,
• Das Integral über die Funktion $f_{t}:=K(t)$ gibt eine Maß an, mit dem man für den Vergleich von Funktionen zu unterschiedlichen Zeitpunkten $t_{1},t_{2}\in T$ ermöglichen kann.

Aufgaben

• Wie kann man Fuzzy-Zugehörigkeitsfunktionen räumlich darstellen und Veränderungen messen? Welche Konsequenzen können sich für die Entscheidungsprozesse und Entscheidungsunterstützung ergeben?
• Betrachten Sie Stromversorgung im Kontext von hoher Verfügbarkeit bei Tag und ggf. fehlender Verfügbarkeit bei Nacht. Wie kann die erforderlichen Speicherkapaziäten in Bezug zwischen Versorgung und Verbrauch über den Tag über Maße beschreiben?

Siehe auch

• Konvexkombination

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Maßtheorie auf topologischen Räumen' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Ma%C3%9Ftheorie%20auf%20topologischen%20R%C3%A4umen/Prozesse%20und%20Nachhaltigkeit
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.