Kurs:Mathematische Modellbildung/Portfolioprüfung

Einführung

Dieses Modul beschreibt, wie die Prüfungsform "Portfolioprüfung" in einer Lehrveranstaltung zur Mathematischen Modellbildung aussehen kann. Diese Hinweise müssen ggf. auf die entsprechenden Rahmenbedingung der Prüfungsordnung an Ihrer Universität angepasst werden. Diese Beschreibung bezieht sich auf eine Modulabschlussprüfung, die an der Universität Koblenz-Landau als mündliche Portfolioprüfung durchgeführt wurde.

Struktur der Prüfung

Die Prüfung gliedert sich in zwei Teile:

• Vorstellung von ausgewählten Teilen aus dem eigenen Portfolio - diese werden von den Prüfer:innen aus dem Portfolio der Studierenden ausgewählt.
• Diskussion und Fragen der Prüfer:innen zu dem Portfolio, z.B. zu Teilen des Portfolios, die in der Vorstellung nicht behandelt werden können.

Ein Portfolio kann aus Zeitgründen nie vollständig in der Prüfung dargestellt werden.

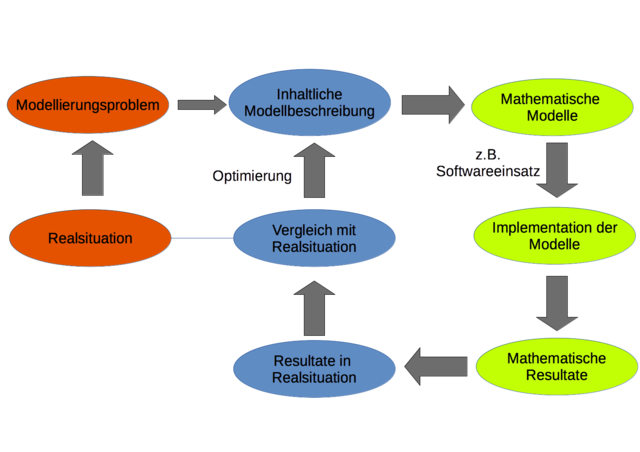
Modellbildungszyklus

Modellbildungszyklus

Beispielthemenbereiche Prüfung

• (Mathematische Grundlagen der Modelle) die Vorstellung der wahrscheinlichkeitstheoretischen, numerischen, geometrischen, ... Grundlagen
• (Modellbildungszyklus) die Vorstellung der Modellierungszyklen: Was war im ersten Modellbildungsansatz unzureichend? Wie wurde das im zweiten Modellierungszyklus verbessert und welche Verbesserung aber auch Grenzen hat das verbesserte mathematisch Modell?
• (Technische Umsetzung) Wie wurde das Modell in Octave, Geogebra, R, Maxima, ... umgesetzt, welche Herausforderungen bestanden, bei der Übersetzung von der mathematischen Theorie in ein auf dem Rechner lauffähiges Modell (Simulation, Visualisierung)
• (Nutzung von Daten) Analyse der Daten, Anwendbarkeit der Daten in dem mathematischen Modell, mögliche Probleme mit der Datengrundlage.

Daten

In der Regel werden mathematische Modelle auf gegebene Daten angewendet, um mit den Daten ein mathematisches Modell zu "trainieren" oder die Güte der mathematischen Modellbildung zu testen. Dies kann auch retrospektiv sein, d.h. Modell macht eine Vorhersage für die Zukunft und wenn in der Zukunft tatsächlich Daten vorliegen, kann man die Vorhersage mit den tatsächlich Daten zu den eingetretenen Ereignissen abgleichen. Die Abweichung kann man z.B. vereinfacht als Maß für die Güte der Vorhersage verstehen.

Optionale Vorbereitungszeit

Für die Portfolioprüfung kann man bei einer speziellen Aufgabenstellung eine Vorbereitungszeit von 90min festlegen.

• Dabei bekommt jeder Prüfling eine individuelle Aufgabenstellung, die dann mit dem vorbereiteten Portfolio aus dem Semester zu einer Präsentation zusammengesetzt wird.
• Die Vorbereitungszeit reicht aus, um aus dem Portfolio die vorbereiteten Inhalte für die Beanwortung der Fragestellung zum Portfolio zu beantworten.
• Die Vorbereitungszeit reicht in keinem Fall aus, das Portfolio erst während der Prüfung zu erstellen!!!

PC-Praktikum - Zusammenhänge und Unterschiede

In der mathematischen Modellbildung werden Softwaretools verwendet, um ein mathematisches Modell in ein Softwaremodell zu übersetzen, das

• das mathematische Modell simuliert,
• Daten verarbeitet und visualisiert oder
• Entscheidungunterstützung basierend auf den Modellierungsergebnissen liefert.

Auswahl von Software für die Portfolioprüfung

In der Präsentation während der Portfolioprüfung wird ein Teil der Modellbildung nach Vorgabe der Prüfer:innen aus dem eigenen Portfolio zur Mathematischen Modellbildung vorgestellt. Vor der Prüfung gibt der Prüfling drei Softwares an, zu denen in der Portfolioprüfung Fragen gestellt werden können. Diese softwarezentrierten Fragen stammen aus den folgenden Bereichen:

• (Einsatzgebiete) Was sind die mathematischen Einsatzgebiete einer speziellen Software und wo liegen deren Grenzen?
• (Vor-/Nachteile) Was kann diese Software besser/schlechter im Vergleich zu anderen Softwares?
• (Einsatz in der mathematischen Modellbildug) Wie wurde die Software ggf. im Portfolio für die mathematische Modellbildung eingesetzt, z.B. für die Visualisierung der Ergebnisse?

Softwareauswahl in der mathematischen Modellbildung

In der mathematischen Modellbildung steht die Modellbildung als solche und deren Ziel im Zentrum. Das PC-Praktikum liefert einen Einblick unterschiedliche Softwaretypen und deren Möglichkeiten (z.B. die Tabellenkalkulation LibreOffice Calc, Octave, R/RStudio, Geogebra, Maxima,... ). In der Modellbildung wird überlegt, mit welcher Software das Ziel der mathematischen Modellbildung am besten erreichen werden kann.

Beispiel: Disaster-Management

Die durch den Klimawandel verursachten Veränderungen in der Häufigkeit und Schwere von Extremereignissen kann für eine bestimmte betroffene Region (z.B. die Eifel) konkret beobachtet werden. Für Regionen mit ähnlichen topographischen Voraussetzungen, die nicht betroffen waren, können mithilfe des mathematischen Modells Prognosen im Falle des Eintretens bestimmter Extremereignisse erstellt werden. So können Risikominimierungsmaßnahmen ausgearbeitet werden, um Schäden für Menschen und Sachschäden so gering wie möglich zu halten. Im mathematischen Modell können Konsequenzen von gewissen optionalen planerischen Entscheidungen abgeschätzt werden, um die beste Risikominimierungsmaßnahme auswählen zu können. Mit einer computergestützten Modellierung können die Auswirkungen der Schutzmaßnahmen für die Bevölkerung abgebildet und visualisiert werden.

Hinweise für die Studierenden

Unter COVID-19 entfällt die Vorbereitungszeit, um Kontaktzeiten zu minimieren. Die Prüfungen finden an der Universität in getrennten Räumen statt. Während der Portfolioprüfung werden Sie aufgefordert, ein Teilthema aus dem bereits bearbeiteten Portfolio vorzustellen, z.B. Modellierungszyklus 3 mit mathematischen Werkzeugen auf Uni-Niveau (z.B. mit numerischen Methoden).

Prüfungszeitspanne 1

• Optional: Wenn es eine Vorbereitungszeit von 90min gibt, werden Sie bereits 90 min vor Prüfungsbeginn in einen Vorbereitungsraum gebeten. Erst im Vorbereitungsraum erhalten Sie die konkrete Aufgabenstellung zu Ihrem Portfolio.
• Bringen Sie Ihr Portfolio auf einem USB-Stick mit, erhalten Sie einen Laptop, mit dem Sie das Portfolio darstellen können, oder
• Sie verwenden Ihr eigenes Laptop. (Sie können auch die IT-Infrastruktur im Prüfungsraum vor der Prüfung ausprobieren - das gibt Ihnen bei der Prüfung Sicherheit).

Prüfungszeitspanne 2

Präsentation und Diskussion des vorbereiteten Portfolios und

• eine Prüfungzeit von 30min, die sich wiederum in
  • 15min Präsentation und
  • 15min Diskussion

gliedert.

Organisatorische Hinweise - Prüfungstakt

Der Prüfungstakt ist ungefähr 45min, da zu der Notenbesprechung und Rückmeldung an die Studierenden noch eine Umbaupause für das Anschließen des Laptops und ggf. für den Aufbau von Veranschaulichungsmaterialien notwendig ist.

Teilbereiche des Portfolios

• Fachmathematischer Hintergrund des Modells - Methoden in einer vergleichende Analyse: z.B. Warum wurde ein stochastischer Ansatz und keine numerische Methode oder geometrischer Ansatz gewählt?
• Auswahlprozess des Modellierungswerkzeuges: z.B. Vorteile der verwendeten Software im Vergleich zu anderer Software
• Berechnungen aus gegebenen Daten oder Testdaten und
• Veranschaulichung von Modellen und deren Implementation
• Grundlagen aus der nicht-mathematischen Disziplin des Modellierungsthemas, aus der das Modellierungsproblem stammt (z.B. Biologie, Physik, Umweltwissenschaften, Sport, Wirtschaft, Sozialwissenschaften, Fremdsprachen, ...).

Erarbeitung des Portfolios

Ein Portfolio entsteht in Gruppenarbeit in dem laufenden Semester und die Erstellung wird in der Lehrveranstaltung/Übung begleitet. Innerhalb der Vorlesung werden einzelne Teilergebnisse vorgestellt und die nächsten Modellierungsschritte besprochen. Die Vorbereitungszeit eine Portfolioprüfung ist daher in keiner Weise ausreichend, das Portfolio selbst zu erarbeiten, sondern man kann lediglich zu der speziell für jeden Studierenden gestellten Portfolioaufgabenstellung aus den erarbeiteten Materialien, die Folien und Inhalte und Resultate zusammenstellen, die für die Präsentation notwendig sind.

Nutzung des Portfolios in der Diskussion

Für die Beantwortung der Fragen in der Diskussion können Sie ebenfalls Folien und mathematische Modelle und Simulationen aus dem Portfolio nutzen. In der Regel sollte die Präsentation mit den erstellten Materialien aus Ihrem Portfolio erfolgen.

• Fragen könnten sich z.B. auf räumliche und zeitliche Modellierung eines Verteilungsprozesses beziehen,
• Simulation einmal live starten und erläutern, wie die mathematische Theorie in der Animation sichtbar wird, bzw. erläutern, warum abweichend zu Annahme bestimmte Artefakte entstehen, die ggf. durch die Art der Diskretisierung der Modelle entstanden sind-.

Niveau-Stufen

Starten Sie in dem Modellierungsproblem mit mathematischen Werkzeugen aus der

• Sekundarstufe I.
• Sekundarstufe II erlaubt dann die Nutzung von Differential- und Integralrechnung.
• Uni-Niveau verwendet explizit Methoden aus den Mathematik-Lehrveranstaltung z.B. Numerik, mehrdimensionale Analysis (wie z.B. Gradientenabstiegsverfahren)

Präsentationsmöglichkeiten in der Vorlesung und Tutorium

Für die Erarbeitung des Portfolios müssen Sie sich ein Semester Zeit geben. Inhaltliche Fragestellungen insbesondere zum Uni-Niveau der Modellbildung können bei Bedarf in der Vorlesung behandelt werden.

Phasen im laufendem Semester

Die Portfolioerstellung erfolgt in dem Semester in fünf Phasen:

• Festlegung des Modellierungsthemenbereiches mit Bezug zum zweiten Fach (z.B. Geographie (Lehramt) oder Naturschutzbiologie (Zwei-Fach-Bachelor))
• Welche Fragestellung sollen durch die Modellbildung beantwortet werden?
• Erster Durchlauf des Modellierungszyklus mit Softwareeinsatz und Identifikation der Schwächen der ersten Modellbildung.
• Zweiter Durchlauf des Modellierungszyklus ebenfalls mit Softwareeinsatz und Begründung, warum durch diesen erneuten Durchlauf eine Verbesserung erfolgt ist.
• Präsentationsübung in der Lehrveranstaltung (Ende Lehrveranstaltung)

Unterstützungsangebot

• Das Unterstützungsangebot erfolgt in der Lehrveranstaltung zur "Mathematischen Modellbildung".
• Eine individuelle Sonderbehandlung für einzelne Studierende, die das Angebot der Vorlesung nicht nutzen und kurz vor Prüfungsbeginn noch "schnell" ein Portfolio zusammenstellen wollen, ist aus zeitlichen Gründen kurz vor der Prüfung nicht möglich.
• Portfolioprüfungen der Lehrveranstaltung beziehen sich immer auf das erstellte Portfolio im laufende Semester und bei Wiederholungsprüfungen auf das Semester, in dem Portfolio erstellt wurde.
• Eine Prüfung kann nur zu dem eigenen erstellten Portfolio in der Lehrveranstaltung abgelegt werden, an dessen Erstellung man aktiv mitgearbeitet hat.

Portfoliothemen

Die Portfoliothemen können

• neu hinzugefügt werden bzw.
• bestehende Themen erweitert werden.

Die Liste der Portfoliothemen zeigen die bearbeiteten Themenbereiche.

Seiteninformation

Diese Lernressource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Wiki-Autoren' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Mathematische_Modellbildung/Portfoliopr%C3%BCfung
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.