Kurs:Mathematische Modellbildung/Themen/Corona-Modellierung/Einführung Teilprojekt 3

Thema

Vergleich der Infektionsverläufe des Covid-19 Virus in 4 ausgewählten Ländern
SIR Modell
dort getroffenen Maßnahmen zur Bekämpfung

Begründung der Länderauswahl

Deutschland: Identifikation durch uns selbst
Italien : sehr früh und sehr stark betroffen
Schweden : meisten Maßnahmen waren freiwillig
Südkorea : geringe Fallzahlen

SIR-Modell

Annahmen^[1]^[2]:

$N$ konstant
Interaktion innerhalb der Gruppen mit gleicher Wahrscheinlichkeit
$S$ -> $I$ -> $R$
Infizierte sind sofort ansteckend

Anfangsbedingungen:

R₀=0
I₀ >0, S₀ >0
α > β

Differentialgleichungen des SIR-Modells

$S'=-\alpha {\frac {SI}{N}}$ , mit α: Infektionsrate

$I'=\alpha {\frac {SI}{N}}-\beta I$ , mit β: Sterberate

$R'=\beta I$

Modellierung

Sekundarstufe I

Erstellen des SIR-Modells für die ausgewählten Länder mithilfe der Tabellenkalkulation

SIR-Modell TK

Modellerstellung mithilfe eines Tabellenkalkulationsprogramms^[3] mit

Zeit $t=t-1$ + Zeitschritt
Infizierbare Personen $S_{t}=N-I_{t}-R_{t}$
Infizierte über "next I": Nächstes I_t: Wenn ${\frac {S_{t}}{N}}$ < 1 und $I_{t}$ * BRZ* ${\frac {S_{t}}{N}}$ >0, dann $I_{t}$ * BRZ_t* ${\frac {S_{t}}{N}}$ . Sonst 0
Genesene Personen $R_{t}=I_{t}+R_{t-1}$
BRZ frei wählbar

Vorgehen

1. Recherchieren der realen Fallzahlen und Verläufe in dem jeweiligen Land
2. Anpassung von BRZ, bis modellierte Kurven mit den realen Kurven übereinstimmen
3. Modellieren, wie sich Verläufe verändern, wenn sich ab bestimmten Zeitpunkten die BRZ erhöhen/verringern

SIR - Schweden

SIR - Südkorea

SIR - Italien

SIR - Deutschland

Sekundarstufe II

Verteilung des Corona-Virus zwischen den Ländern
Integrierung einer Transportmatrix in das SIR-Modell

Grundlagen Matrizenrechnung

lineares Gleichungssystem der Form $A*x=b$
Matrizenmultiplikation nur wenn im Falle $A=lxm$ und $B=mxn$
Beispielhafte Erklärung: $2x2$ Matrix $A$ und $2x1$ Vektor $b$

$\left({\begin{array}{cc}a&b\\c&d\end{array}}\right)\left({\begin{array}{c}x\\y\end{array}}\right)=\left({\begin{array}{c}ax+by\\cx+dy\end{array}}\right)$

Anwendung auf Flugverkehr

$\left({\begin{array}{cc}a_{ii}&a_{ji}\\a_{ij}&a_{jj}\end{array}}\right)\left({\begin{array}{c}x_{i}\\x_{j}\end{array}}\right)=\left({\begin{array}{c}x'_{i}\\x'_{j}\end{array}}\right)$

$a_{ii}$ : Anteil der in Land i Bleibenden [%]
$a_{ij}$ : Anteil der Reisenden von Land i nach Land j [%]
Vektor $x$ : Einwohnerzahlen von Land i und Land j
Vektor $x'$ : Einwohnerzahlen der Länder nach Transportprozess

Abschätzung, wie viele Flugpassagiere von einem Land zum anderen fliegen:

Annahme $a_{ij}$ = $a_{ji}$
Berechnung $a_{ij}={\frac {n_{i}n_{j}}{n}}$ mit $n$ abfliegenden Personen pro Tag weltweit und $n_{k}$ abfliegenden Personen pro Tag des Landes $K$
Flüge unabhängig von der Entfernung der Länder und der Zeit

Beispiel: Transportprozesse zwischen Schweden und Südkorea

$\left({\begin{array}{cc}1-{\frac {n_{i}n_{j}}{nS_{i}}}{\frac {S_{i}}{N_{i}}}&{\frac {n_{i}n_{j}}{nS_{j}}}{\frac {S_{j}}{N_{j}}}\\{\frac {n_{i}n_{j}}{nS_{i}}}{\frac {S_{i}}{N_{i}}}&1-{\frac {n_{i}n_{j}}{nS_{j}}}{\frac {S_{j}}{N_{j}}}\end{array}}\right)_{t}\left({\begin{array}{c}S_{i}\\S_{j}\end{array}}\right)_{t}=\left({\begin{array}{c}S'_{i}\\S'_{j}\end{array}}\right)_{t}$

$I$ und $R$ lassen sich analog bestimmen

$(S_{k})_{t}=N_{k}-(I_{k})_{t}-(R_{k})_{t}$

Matrixeinbindung in LibreOffice

"next I" _SW: $I_{t,SW}$ * BRZ * ${\frac {S_{t,SW}}{N_{SW}}}$ - ${\frac {n_{i}n_{j}}{n}}$ * ( ${\frac {I_{t-1,SW}}{N_{SW}}}$ - ${\frac {I_{t-1,SK}}{N_{SK}}}$ )

Infektionsgeschehen in Südkorea und Schweden im Transportmodell

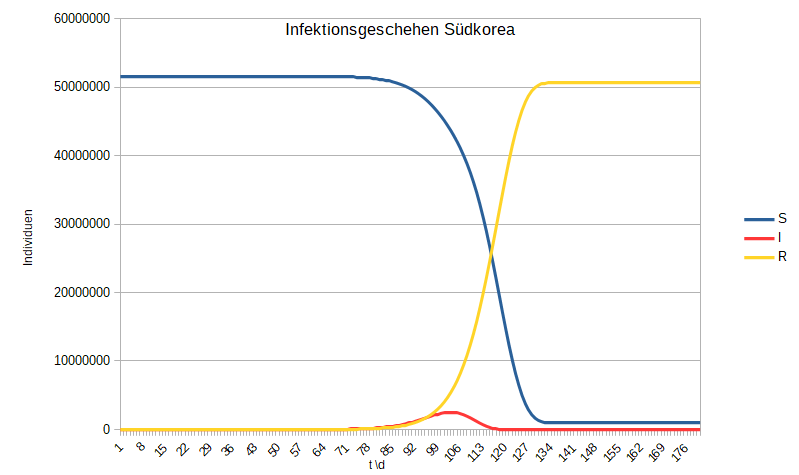
Erste Infizierte Person in Schweden an Tag 46 (+/- 3 Tage)
Infektionsgeschehen in Schweden schneller (15 Tage weniger bis Maximum)

Uniniveau

Konzept

Ziel: Funktion finden, die die Neuinfektionen abbildet
Logistisches Wachstum über Bernoulli-DGL
Graph der Lösung $f(t)$ der B.-DGL entspricht Kurve der kummulierten Infiziertenzahl
Ableitung $f'(t)$ der Lösung $f(t)$ entspricht der Kurve der Neuinfektionen
nichtlineare Regression in R Studio
Vergleich der Länder über ausgegebene Parameter

Bernoullische Differentialgleichung

Einschub: $\;$ Bernoullische Differentialgleichung

Eine DGL der Gestalt $f'(t)=kGf(t)-kf^{2}(t)$ lässt sich wie folgt lösen:

$g(t)={\frac {1}{f(t)}}\Rightarrow g'(t)=-{\frac {f'(t)}{f^{2}(t)}}$

$g'(t)=-{\frac {kGf(t)-kf^{2}(t)}{f^{2}(t)}}=-kGg(t)+k$

Lösung der Bernoullische Differentialgleichung

Lösen der homogenen DGL

$g_{h}'(t)+kGg_{h}(t)=0$ ergibt

$g_{h}(t)=g_{0}e^{-kGt+\delta }$ mit $\delta =kGc$ die partikulare Lösung ist

$g_{p}(t)={\frac {k}{kG}}-{\frac {1}{G}}e^{-kGt+\delta }$ und mit $g(0)=g_{0}={\frac {1}{f_{0}}}={\frac {1}{f(0)}}$ ergibt sich:

$g(t)={\frac {1}{G}}+\left({\frac {1}{f_{0}}}-{\frac {1}{G}}\right)e^{-kGt+\delta }$
Da $f(t)={\frac {1}{g(t)}}\Rightarrow f(t)={\frac {G}{1+({\frac {G}{fo}}-1)e^{-kGt+\delta }}}$

Parametisierung

Durch Parametisierung $f(t)\;{\overset {allg.}{=}}\;\left({\frac {4A}{\alpha \left(1+e^{-\alpha (t-c)}\right)}}\right)$

Beidseitige Ableitung der Bernoullische DGL:

$f'(t)=\left({\frac {4Ae^{-\alpha (t-c)}}{\left(1+e^{-\alpha (t-c)}\right)^{2}}}\right)$ ist eine Lösung der DGL $f''(t)=kGf'(t)-2kf(t)f'(t)$ .

SIR: DGL

SIR-Modell

Für das SIR-Modell werden drei DGL verwendet ( $N=const.$ ):

$S'=-\alpha {\frac {SI}{N}}$

$I'=\alpha {\frac {SI}{N}}-\beta I$

$R'=\beta I$

Es gilt $N=S+I+R=const.$

Lösung der DGL nach Näherung

Die DGL für die Infiziertenzahl lässt sich also wie folgt schreiben:

${\begin{cases}I'&=\alpha {\frac {(N-R-I)}{N}}I-\beta I=\left(\left(1-{\frac {R}{N}}\right)\alpha -\beta \right)I-{\frac {\alpha }{N}}I^{2}\\&=\left(\left(1-{\frac {\beta }{N}}\int Idt\right)\alpha -\beta \right)I-{\frac {\alpha }{N}}I^{2}\end{cases}}$

Vernachlässigung des letzten Terms $\left(-{\frac {\alpha }{N}}I^{2}\right)$ :

$I'=(\alpha -\beta )I-{\frac {\alpha \beta }{N}}\int Idt\cdot I$

vergleiche $I(t)$ mit $f'(t)$ ; mit $f'(t)$ aus der Ableitung der B.-DGL

$\left(I(t)=\left({\frac {4a\cdot k\cdot e^{-k(t-c)}}{\left(1+e^{-k(t-c)}\right)^{2}}}\right)\right)$

Modellierung der Infiziertenzahl

nicht lineare Regression mit der Methode der kleinsten Quadrate
Kurvenanpassung an (bspw. $n$ ) Werte durch Minimerung des Abstandquadrates der Messpunkte zu der Fitkurve über die Veränderung der Parameter:

$min{\underset {i=n}{\overset {n}{\sum }}}(y_{i}-f(x_{i}))^{2}$
Minimum finden über $\left(2{\underset {n}{\sum }}(y_{i}-f(x_{i}))\right)f'(x_{i}){\overset {!}{\approx }}0$

Schätzintervall für die Werte von $a,\;c$ und $k$ (Werte liegen zu $95\;\%$ darin)

${\frac {ak}{N}}$ : Schwere der Epidemie

$k$ : Ausbreitungsgeschwindigkeit

$c$ : Dauer zum vorläufigen Höhepunkt der Epidemie

Ergebnis

Schwere der Pandemie in Italien am höchsten, in Südkorea am geringsten
Südkorea höchste Ausbreitungsgeschwindigkeit
Schweden geringste Ausbreitungsgeschwindigkeit
Italien: Peak der Neuinfektionen am frühsten (Tag 35)
Schweden Peak am spätesten (Tag 53)

Beispiel: Deutschland

Optimierung

Verbesserte Anpassung der Kurve durch die Ableitung der Gompertz-Funktion (asymmetrische Sigmoidfunktion)

$I(t)=a\cdot b\cdot e^{\left(-e^{(-b\cdot (t-c)}-b\cdot (t-c)\right)}$

Parameter analog zur vorherigen Funktion, nur $b$ durch $k$ ersetzt
[Geogebra: Parametereinstellungen der Fitfunktion]

Ergebnis

Ergebnisse ähnlich wie in Tabelle davor
Schwedens Peak wird 4 Tage früher erreicht
Ausbreitungsgeschwindigkeit Italiens unterscheidet sich deutlicher von der Schwedens

Beispiel: Deutschland

Vergleich

Siehe auch

Seiteninformation

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Mathematische Modellbildung' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Mathematische%20Modellbildung/Themen/Corona-Modellierung/Einf%C3%BChrung%20Teilprojekt%203
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

Literatur / Quellennachweis

[1] ttps://imsc.uni-graz.at/keeling/modI_ss09/projekten/DzuburReicherSchmidEnd.pdf

[2] ttps://flexikon.doccheck.com/de/SIR-Modell

[3] ttps://niebert.github.io/wikiversity_files/index.html

[1]

[2]

[3]

Thema

Begründung der Länderauswahl

SIR-Modell

Annahmen[1][2]:

Differentialgleichungen des SIR-Modells

Modellierung

Sekundarstufe I

SIR-Modell TK

Vorgehen

SIR - Schweden

SIR - Südkorea

SIR - Italien

SIR - Deutschland

Sekundarstufe II

Grundlagen Matrizenrechnung

Anwendung auf Flugverkehr

Abschätzung, wie viele Flugpassagiere von einem Land zum anderen fliegen:

Beispiel: Transportprozesse zwischen Schweden und Südkorea

Matrixeinbindung in LibreOffice

Infektionsgeschehen in Südkorea und Schweden im Transportmodell

Uniniveau

Konzept

Bernoullische Differentialgleichung

Lösung der Bernoullische Differentialgleichung

Parametisierung

SIR: DGL

Lösung der DGL nach Näherung

Modellierung der Infiziertenzahl

Ergebnis

Beispiel: Deutschland

Optimierung

Ergebnis

Beispiel: Deutschland

Vergleich

Siehe auch

Seiteninformation

Literatur / Quellennachweis

Annahmen^[1]^[2]: