Kurs:Mathematische Modellbildung/Themen/Corona-Modellierung

Themen und Zielsetzung[Bearbeiten]

Im Folgenden werden dem Modellierungsthema Nachhaltigkeitsziele zugeordnet.^[1]

Verteilung von Corona-Aerosolen in Klassenzimmern[Bearbeiten]

Das Jahr 2020 wird vom Covid-19 Virus überschattet. Schulen mussten schließen, die Wirtschaft stand fast still. Nach einer ersten Eindämmung des Virus' durften Schulen wieder öffnen, allerdings nur mit einem gültigen Hygienekonzept, das neben der bekannten AHA-Regeln auch ein Lüften der Klassenzimmer in regelmäßigen Abständen vorsieht. In diesem Projekt werden in mathematischen Modellbildungsprozessen die Verteilung von (Corona-)Aerosolen und die Qualität der Luft in verschiedenen Bereichen eines Klassenzimmmers näher betrachtet und modelliert. Auf dieser Grundlage werden die Luftqualität im Raum nach dem Lüften und ihre Auswirkungen auf die Verteilung der Schüler*innen untersucht.

Auswirkung der Corona-Pandemie auf die Gastronomie[Bearbeiten]

Durch die Corona-Pandemie im Jahr 2020 steht Deutschland vor einer der härtesten Herausforderungen des 21. Jahrhunderts. Durch zahlreiche Einschränkungen wurde dabei die Wirtschaft besonders hart getroffen. Geschäfte und Restaurants mussten schließen, viele ArbeitnehmerInnen verloren ihre Anstellung. In unserem Portfolio möchten wir speziell die Branche der Gastronomie betrachten und dabei die Verteilung staatlicher Mittel auf verschiedenste Weisen mathematisch modellieren.

Vergleich der Coronaverläufe und Maßnahmenergreifung ausgesuchter Länder[Bearbeiten]

2019 begann die globale Ausbreitung des Coronavirus. In unterscheidlichen Ländern wurden verschiedene Maßnahmen getroffen, um das Virus einzudämmen. Das Projekt behandelt die Unterschiede in Verlauf und Stärke des Virus in Zusammenhang mit ergriffenen Maßnahmen in den Ländern Südkorea, Italien, Schweden und Deutschland.

Aufgaben[Bearbeiten]

Das Portfolio wird während des Semesters erstellt. Ergänzen Sie jeweils hier die bereits bearbeitenden Teilaufgaben für hinter der Bezeichnung für Ihr Portfolio - z.B. (A1)

Teilprojekt 1: (A1)
Teilprojekt 2: (A1)

Gruppenmitglieder[Bearbeiten]

Nennen Sie hier die Wikiversity User-Accounts, die an diesem Projekt mitgearbeitet haben. Die Versionsgeschichte des Portfolios zeigt, wer welche Beiträge zum Portfolio geleistet hat. Geben Sie auch an, in welchem Teilprojekt Sie mitgearbeitet haben.

Teilprojekt 1: Katrin Cimniak, Jan Lucas Fischer, Rebecca Hostert, Yannick Strauß
Teilprojekt 2: Selina Hoffmann, Lukas Rupp, Sebastian Scherer und Maximilian Kunz (Kuntz)
Teilprojekt 3: Rose Stojanova, Stefan Sänger, Tugba Taskin, Shivani Osterauer

Wiki2Reveal Präsentationen[Bearbeiten]

Sie können in Wikiversity Wiki2Reveal-Präsentationen erstellen, die Sie für die Portfolio-Präsentation in der Prüfung verwenden können. Listen Sie hier die verwenden Präsentationen.

Zuordnung zu Nachhaltigkeitszielen[Bearbeiten]

Wählen Sie hier die Nachhaltigkeitsziele aus, die Sie in Ihrem Modellierungsprojekt addressieren.

SDG3: Good Health and Well-being

Die Gesundheit der Bevölkerung ist die Grundlage einer modernen Gesellschaft. Die COVID-19 Pandemie hat offensichtlicherweise direkten Einfluss auf die Gesundheit von Milliarden Menschen und belastet das Gesundheitssystem und die Wirtschaft verschiedenster Länder. Es ist also im Interesse Aller die Pandemie durch funktionierende Hygienekonzepte und Kontaktbeschränkungen einzudämmen. Für die Kontrolle der Effektivität solcher Konzepte eignet sich die mathematische Modellbildung.

SDG4: Quality Education

Für eine qualitativ hochwertige Bildung ist Präsenzunterricht unabdingbar. Als dieser im Frühjahr 2020 durch Homeschooling-Maßnahmen ersetzt werden musste, gingen viele wichtige Faktoren des Unterrichts verloren. Denn in der Schule sollen nicht nur fachwissenschaftliche Lerninhalte vermittelt werden, sondern auch Methoden und soziale Kompetenzen stehen im Mittelpunkt. Für den Präsenzunterricht ist eine Risikominimierung der Ansteckungsgefahr enorm wichtig, die Gesundheit der Schüler*innen und Lehrer*innen ist das oberste Ziel. Dies ist ohne geeignete Hygienekonzepte nicht möglich. Der Hauptbestandteil ist neben dem Tragen der Masken in den Pausen und teilweise im Unterricht das regelmäßige Lüften der Klassenräume. Daher beschäftigt sich ein Teilprojekt des Kurses genau mit diesem Thema. Denn eine qualitativ hochwertige Bildung ist die Grundlage unserer heutigen Gesellschaft.

SDG8: Decent Work and Economic Growth

Aufgrund der COVID-19 Pandemie kam es zu erheblichen Einbußen in der Gastronomie. Durch die Schließung der Gastronomie während des 1. und 2. Lockdowns war ein wirtschaftliches Wachstum nicht möglich. Nun ist es wichtig, dass die Gastronomen überleben und die Wirtschaft wieder wächst. Um dies zu erreichen, sollen staatliche Zuschüsse die Defizite ausgleichen. Mit Hilfe der mathematischen Modellbildung kann bestimmt werden, wie hoch die staatlichen Zuschüsse seien müssen, damit die Gastronomen überleben können.

SDG10: Reduced Inequalities

Bei der Auszahlung der staatlichen Zuschüsse kann es zu einer Ungleichheit kommen. Um diese Ungleichheit zu reduzieren, wird eine „gerechte“ Verteilung der staatlichen Zuschüsse benötigt. Für das Konzept einer „gerechte“ Verteilung ist die mathematische Modellbildung geeignet.

SDG16: Peace, Justice and Strong Institutions

Durch den Modellierungsansatz sollen stabile und gerechte Strukturen unterstützt werden. Dabei sollen die staatlichen Zuschüsse gerecht verteilt werden, das heißt jedes Unternehmen soll dieselbe Chance haben, zu überleben.

Rohdaten[Bearbeiten]

Für die Modellierungszyklen sind die folgende Rohdaten verwendet. Rohdaten können entweder tatsächliche existierende Rohdaten sein, auf die Sie zugreifen, oder zufällig nach einer Verteilung generierte Daten sein, auf die Sie die Modellierung anwenden.

Daten: Modellierungszyklus 1[Bearbeiten]

Quelle angeben, Methode zur Generierung der Zufallsdaten beschreiben.

Teilprojekt 1:[Bearbeiten]

Quellen:^[3]

Teilprojekt 2:[Bearbeiten]

Quellen:

Staatliche Novemberhilfen

Informationen für Unternehmen/Selbstständige

Auswirkungen des Coronavirus auf das Hotel und Gastgewerbe

Pressemitteilung Corona-Krise trifft Gastronomie hart

Liquidität

Insolvenz

Rentabilität

Betriebswirtschaftlicher Erfolg

Coronavirus SARS-CoV-2: Chronik der bisherigen Maßnahmen

Unternehmenskalkulation

Arithmetisches Mittel

Teilprojekt 3[Bearbeiten]

Vergleich der Länder

Quellen:

Daten: Modellierungszyklus 2[Bearbeiten]

Daten: Modellierungszyklus 3[Bearbeiten]

Niveauzuordnung[Bearbeiten]

Teilprojekt 1[Bearbeiten]

Sekundarstufe I:[Bearbeiten]

zweidimensionale Betrachtung des Klassenzimmers

Bewertung der Lüftungseffektivität über Abstandsberechnungen zu "Lüftungsstrecken"

Nutzung von Trigonometrie, Satz des Pythagoras und Kosinussatz

Darstellung der Intensität des Luftstroms einzelner Fenster durch verschiedene Farbintensitäten

Sekundarstufe II:[Bearbeiten]

Idee: Luftstrom und Raum dargestellt mit Vektoren
Modell um eine Dimension erweitern (3-dimensionales Modell)
Normen, Metriken, Topologie (Foliensatz)

Universität:[Bearbeiten]

quantitative Auswertung der Lüftungsgüte durch mehrdimensionale Analysis
Optimierung der Sitzpositionen der Schülerinnen und Schüler durch Gradientenabstiegsverfahren

Comsol 2D:[Bearbeiten]

zweidimensionale Betrachtung des Klassenzimmers in der Vogelperspektive
Darstellung der Luftströmung im Klassenzimmer auf Grundlage von Navier-Stokes-Gleichungen zur Fluiddynamik
Partikelbewegung der Aerosole der gesunden und erkrankten Personen entlang der Luftströmungen
Risikobewertung abhängig von der Position der Personen und der Partikelbewegung auf der Fläche

Comsol 3D:[Bearbeiten]

dreidimensionale Betrachtung des Klassenzimmers
Darstellung der Luftströmung im Klassenzimmer auf Grundlage von Navier-Stokes-Gleichungen zur Fluiddynamik
Partikelbewegung der Aerosole der gesunden und erkrankten Personen entlang der Luftströmungen
Risikobewertung abhängig von der Position der Personen und der Partikelbewegung im Raum

Teilprojekt 2:[Bearbeiten]

Sekundarstufe I:[Bearbeiten]

Einfache Tabellenkalkulation (Einnahmen, Ausgaben, Gewinn verschiedener Unternehmen)
Gewinn berechnen
Kostendeckungsgrad berechnen
Berechnung des arithmetischen Mittels
Gleiche Verteilung der staatlichen Mittel auf alle Unternehmen (Einfache Division)
Vergleich des Kostendeckungsgrades in einem Säulendiagramm
Lineare Funktionen

Sekundarstufe II:[Bearbeiten]

Vektorrechnung in $\mathbb {R} ^{2}$
Vektorgleichung einer Geraden (Parameterform)
Berechnung der $x_{1}$ -Komponente eines Punkts durch Einsetzen in Parametergleichung der Geraden (Gleichungssystem lösen)

Universität:[Bearbeiten]

Aufstellen einer Kostenfunktion mit mehreren Variablen
2-dimensionale Intervallschachtelung
Komplexere Operationen mit Tabellenkalkulationsprogramm

Teilprojekt 3:[Bearbeiten]

Sekundarstufe I:[Bearbeiten]

Modellerstellung mithilfe eines Tabellenkalkulationsprogramms. Tabelle zu dem SIR-Modell mit den Spalten

t(Zeit)
S(Personen, diesich potenziell mit dem Virus anstecken können)
I(aktuell Infizierte)
R (Recovered, genesene Personen)
BRZ (Basisreproduktionszahl, die Anzahl an Personen,die eine infizierte Person im Durchschnitt ansteckt)
nächstes I (Anzahl infizierte Personen nach einem Zeitschritt)

Berechnung der einzelnen Felder[Bearbeiten]

t2: t1+ Zeitschritt
S2: Einwohnerzahl - I1 - R2
I2: Wenn("nächstes I"1 + R1 <= Einwohnerzahl; "Nächstes I"1; Einwohnerzahl - R2)
"Nächstes I"1: WENN(UND(S1/Einwohnerzahl <1; I1 * BRZ1 *(S1/ Einwohnerzahl)>0); I1* BRZ1 *(S1/ Einwohnerzahl);0)
BRZ ist frei wählbar und verändert die anderen davon Abhängigen Variablen

Sekundarstufe II:[Bearbeiten]

Modellbildung zur Verteilungund Bewegung der Personen zwischen den Ländern Deutschland, Schweden, Südkorea und Italien.

Matrizenrechnung
A ist 4x4 Matrix mit den prozentualen Bewegungen zwischen den Ländern,b ist 3x1 Vektor mit den Einwohnerzahlen
Berechnung mit Maxima

Universität:[Bearbeiten]

SIR-Modell mithilfe von Differentialgleichungen darstellen
S'(t)= -α*S(t)*I(t)
I'(t)= α*S(t)*I(t)-β*I(t)
R'(t)= β*I(t)
mit α= Infektionsrate und β= Genesungsrate
Lösen der Differentialgleichungen mit R Studio

Modellierungszyklen[Bearbeiten]

In den Modellierungszyklen wird schrittweise

modelliert,
bewertet und
ein Optimierungsvorschlag gemacht, der in den nächsten Modellierungszyklus einfließt

Teilprojekt 1[Bearbeiten]

Modellierungszyklus 1 - Niveau Sekundarstufe 1[Bearbeiten]

Modell 1[Bearbeiten]

Im ersten Modell wird die Lüftungseffektivität im Raum durch die Bestimmung des Abstands der Raumpunkte zu den stark belüfteten Bereichen bewertet. Zur Vereinfachung des Modells für die Sekundarstufe 1 wird das Klassenzimmer als zwei dimensionales Rechteck dargestellt. Das Lüften des Raumes geschieht durch einen Luftstrom zwischen der Tür und den verschiedenen Fenstern und wird durch jeweilige Verbindungsstrecken dargestellt.

Um zu bewerten, wie effektiv ein beliebiger Punkt im Klassenzimmer bei der Öffnung der Fenster belüftet wird, wird der Abstand von dem Punkt zu der jeweilig am nächsten liegenden Lüftungsstrecke zwischen Tür und Fenster berechnet. Je kleiner der Abstand ist, desto effektiver wird der Raumpunkt belüftet. Für diese Berechnung werden der Satz des Pythagoras, der Kosinussatz und der Sinus genutzt.

Berechnungen[Bearbeiten]

Der beliebige Raumpunkt wird als $P$ bezeichnet. Zunächst werden drei rechtwinklige Hilfsdreiecke konstruiert. Die Hypotenuse des ersten Dreiecks ist $[P,Fenster]=c$ . Die Katheten ergeben sich durch die Senkrechte von $P$ zur Fensterwand $[P,Fensterwand]=a$ und $[Fensterwand,Fenster]=b$ . Die Längen der Strecken $a$ und $b$ lassen sich im Koordinatensystem mithilfe der Koordinaten von Punkt $P$ ablesen. Die Strecke $c$ lässt sich anschließend mithilfe des Satz des Pythagoras berechnen.

c={\sqrt {a^{2}+b^{2}}}

Analog hierzu wird das zweite Hilfsdreieck konstruiert, um die Strecke $[P,T{\ddot {u}}r]=d$ zu berechnen.

Der Abstand $[Fenster,T{\ddot {u}}r]=e$ wird ebenfalls über den Satz des Pythagoras ermittelt. Die Katheten bilden hier eine Senkrechte von dem Fenster zur Wand und von die Strecke von diesem Schnittpunkt zur Tür.

Der Winkel $\angle P,T{\ddot {u}}r,Fenster=\alpha$ wird mithilfe des Kosinussatz berechnet.

\alpha =\arccos({{e^{2}+d^{2}-c^{2}} \over {2ed}})

Der Abstand $s$ von Punkt $P$ zu der Strecke $e$ ist durch die Länge der Senkrechten von $e$ auf $P$ gegeben. Diese Länge kann mithilfe des Sinus berechnet werden.

s=d\cdot sin{\alpha }

Falls der nächstgelegene Punkt auf der Lüftungsstrecke der Endpunkt der Strecke am Fenster ist, berechnet sich der Abstand einfach über den Satz des Pythagoras. Er ist die Länge der Hypothenuse des rechtwinkligen Hilfsdreiecks.

Modell 2[Bearbeiten]

Im zweiten Modell ist der Fokus auf die Qualität des Lüftens gerichtet, Qualität meint in diesem Sinne, welcher Bereich des Raumes den größten Luftmassenaustausch erfährt. Wie im ersten Modell wird das Klassenzimmer vereinfacht zweidimensional dargestellt. Da aufgrund der momentanen Situation keine realen Messwerte des Volumenstroms gemessen werden konnten, wurden folgende Annahmen getroffen:

Im Bereich von Fenster 1 zur Tür herrscht der größte Volumenstrom, im Bereich zwischen Fenster 4 und Tür der kleinste.

Überschneidungen der Flächen fließen additiv in das Modell ein.

Kleine Bereiche neben den Fenstern erfahren einen Volumenstrom, allerdings kleiner als im direkten Lüftungsbereich.

Anhand dieser Annahmen, die im Unterricht mit Schülern mit Hilfe von Windmessgeräten geprüft werden können, entsteht eine Übersicht, auf welcher man stark belüftete und schwach bzw. gar nicht belüftete Bereiche direkt erkennt. Je dunkler der Farbton, desto besser ist dieser Bereich belüftet, je heller, desto schwächer. Es ist erkennbar, dass die rechte untere Ecke des Raumes nach diesem Modell keinen Luftaustausch erfährt.

Bewertung Modellierungszyklus 1[Bearbeiten]

Ziel des Modellierungszyklus war es, die Luftqualität innerhalb eines Klassenzimmers beim Lüften zu untersuchen und Aussagen darüber treffen zu können, wie die Luftqualität im Raum aufgrund des Lüftens ist.

In Modell 1 ist es möglich, eine Aussage bezüglich der Luftqualität zu allen Punkten der Ebene zu treffen. Somit ist die allgemeine Zielsetzung erfüllt. Allerdings ist es in Modell 1 schwer, einen Überblick über die Luftqualität im gesamten Raum zu erhalten. Zudem sind die Lüftungsbereiche nur als Linien dargestellt, was nicht der Realität entspricht, aber das Modell vereinfacht ohne die Aussagekraft zu verringern. In Modell 2 ist das Ziel, die Schwächen, die Modell 1 aufweist, auszugleichen. So sind in diesem Modell die Luftströme als Flächen eingezeichnet mit unterschiedlich starker Lüftungsintensität. Modell 2 bietet einen guten Überblick, wie die Luftqualität im gesamten Raum ist. Somit führen beide Modelle zur Beantwortung der Frage nach der Luftqualität im Klassenzimmer, allerdings zum einen mit dem Schwerpunkt, einzelne Raumpunkte zu betrachten und zum anderen mit dem Schwerpunkt, einen Gesamteindruck über die Luftqualität im gesamten Klassenzimmer zu erhalten.

Vor allem anhand des zweiten Modells lassen sich nun gut Bereiche erkennen, in denen die Schüler*innen sitzen sollten. Bei der Verteilung ist natürlich trotzdem der Sicherheitsabstand zu beachten. Aufgrunddessen und des doch eher kleinen Bereiches, der gut belüftet ist, sollten auf keinen Fall Klassen mit 25+ Schüler*innen unterrichtet werden. Die Lehrkraft könnte mit ausreichend Abstand zu den SuS im rechten Bereich platziert werden, sodass der gut belüftete Teil des Raumes bestmöglich von SuS besetzt werden kann.

Optimierung Modellierungszyklus 1[Bearbeiten]

Bisher wurde der Klassenraum zweidimensional betrachtet. Eine dreidimensionale Modellierung könnte nochmal bessere Aussagen darüber treffen, ob der Luftstrom in den Bereichen auch größer ist, welche den Aerosol-Ausstoß betreffen. Zusätzlich wurde bisher angenommen, dass zwischen einem Fenster und der Tür der Volumenstrom gleichbleibt, allerdings ist davon auszugehen, dass vom Fenster zur Tür hin der Strom zu- oder abnimmt. Im zweiten Modell treten viele unbelüftete (im Modell weiße) Bereiche auf. Vermutlich sind diese nicht komplett unbelüftet und weiterhin ist davon auszugehen, dass weiße Bereiche in Fensternähe stärker als weiße Bereiche in der rechten unteren Raumecke belüftet sind. Des Weiteren ist eine Abstandsbetrachtung von Punkt zu der Gerade, die von Tür zu Fenster verläuft, nur in einem gewissen Bereich sinnvoll. Beispielsweise ist in der rechten oberen Ecke der Abstand zum Fenster 4 relevant, da der Lotfußpunkt zur Gerade außerhalb des Klassenzimmers liegt.

Modellierungszyklus 2 - Niveau Sekundarstufe 2[Bearbeiten]

Einführung[Bearbeiten]

Im zweiten Modellierungszyklus sollen die Modelle des ersten Modellierungszyklus verbessert werden. Dafür wird das Klassenzimmer nicht mehr als zweidimensionale Ebene, sondern als dreidimensionaler Körper betrachtet. Somit wird ermöglicht, allen Punkten im Raum eine Luftgüte zuzuordnen.

In der Weiterentwicklung des zweiten Modells werden im 3D-Modell Luftströme als schiefe Pyramidenstümpfe dargestellt. Hierbei wird weiterhin angenommen, dass nicht nur der Bereich zwischen Tür und jeweiligem Fenster belüftet wird, sondern auch ein kleiner zusätzlicher Teil um die Fenster und Türen herum. Somit entstehen etwas größere Luftstromkanäle. Der Abstand des zu betrachtenden Raumpunkts zu der Oberfläche der Pyramidenstümpfe lässt auf die Luftqualität an diesem Raumpunkt schließen. Je kleiner der Abstand zur Oberfläche ist, desto besser ist die Luftqualität an diesem Punkt. Die Oberflächen der schiefen Pyramidenstümpfe werden als Ebenen dargestellt. Mit Hilfe der Analytischen Geometrie kann der Abstand von Punkt und Ebene bestimmt werden.

Dabei entstehen allerdings neue Probleme: Durch die vier schiefen Pyramidenstümpfe entstehen insgesamt 16 Ebenen, zu denen der Abstand der Raumpunkte bestimmt werden könnte. Zudem können nicht für alle Raumpunkte die Abstände zu den Flächen berechnet werden, da sich kein Lot zur Ebene der Oberfläche durch den Raumpunkt konstruieren lässt. In diesen Fällen müsste der Abstand der Punkte zu den Kanten der schiefen Pyramidenstümpfe berechnet werden. Somit wird dieses Modell in der Berechnung und der Zuordnung der Gerade oder Ebene, die am nächsten ist, außerordentlich komplex.

In der Überarbeitung des Modells werden im dreidimensionalen Klassenzimmer nun Geraden verwendet, um den Luftstrom darzustellen. Die Geraden gehen jeweils durch den Schwerpunkt der Türe und den Schwerpunkt des jeweiligen Fensters. Durch diese Vereinfachung verliert das Modell im Vergleich zum ursprünglichen Modell nicht an Aussagekraft, die Berechnung wird aber vereinfacht.

Berechnung[Bearbeiten]

Vorgehensweise[Bearbeiten]

Um die Lüftungsgüte eines einzelnen Raumpunktes zu bestimmen wird, wie im ersten Modell, der Abstand des Punktes zu den Schwerpunktgeraden zwischen der Tür und den Fenstern als Indikator herangezogen. Der kleinste Abstand vom Raumpunkt zu einer Strecke wird, je nach Lage des Punktes, mithilfe des Lotfußpunkt aus der analytischen Geometrie bestimmt oder ist als Abstand zwischen dem Schwerpunkt des jeweiligen Fensters und dem Raumpunkt definiert. Anders als im ersten Modellierungszyklus wird nicht nur der Abstand zu einer einzelnen Strecke als relevant angesehen. Es werden stattdessen die Abstände zu allen Strecken in Kombination betrachtet. So kann besser berücksichtigt werden, dass beispielsweise Bereiche zwischen zwei Fenstern besser belüftet werden, als Bereiche neben einem Äußeren Fenster. Die Lüftungsgüte wird so normiert, sodass sie auf jede einzelne Strecke bezogen nur einen Wert zwischen Null und Eins erreichen kann, wobei eins eine optimale Lüftung, und Null keine Lüftung darstellt. Die Lüftungsgüte der einzelnen Strecken werden daraufhin addiert, sodass die Gesamtlüftungsgüte Werte zwischen Null und Vier erreichen kann.

Beispielrechnung[Bearbeiten]

Es soll zunächst der Abstand von einem beliebigen Punkt $P$ zu allen Strecken, welche von der Tür zu einem der vier Fenster verlaufen, berechnet werden.

Betrachte dazu beispielhaft den Abstand des Punktes $P$ zur Strecke $\epsilon$ , welche von der Tür zu Fenster 4 verläuft. Punkt $T$ sei der Mittelpunkt der Tür, Punkt $F_{4}$ der Mittelpunkt des vierten Fensters. Die Gerade $e$ ist die Trägergerade der Strecke $\epsilon$ . Um den Abstand von $P$ zur Geraden $e$ zu bestimmen, benötigen wir die Geradengleichung von $e$ : ${\vec {x}}={\vec {T}}+\lambda \cdot ({\vec {F_{4}}}-{\vec {T}})$ . Bestimme nun den Abstand von $P$ zu $e$ mithilfe des Lotfußpunktverfahren. Die Normalengleichung der Hilfsebene $h_{4}$ lautet dann: $({\vec {P}}-{\vec {x}})\cdot ({\vec {F_{4}}}-{\vec {T}})=0$ . Bestimme nun den Schnittpunkt der Gerade $e$ und der Hilfsebene $h_{4}$ durch Einsetzen der Geradengleichung in die Ebenengleichung: $({\vec {P}}-({\vec {T}}+\lambda \cdot ({\vec {F_{4}}}-{\vec {T}})))\cdot ({\vec {F_{4}}}-{\vec {T}})=0$ . Auflösen nach Parameter $\lambda$ und anschließendes Einsetzen in die Geradengleichung von $e$ ergibt den Lotfußpunkt $LF_{4}$ von $P$ auf $e$ .

Fall 1:

Der Lotfußpunkt

LF_{4}

liegt innerhalb des Klassenzimmers

[0;9]

x

[0;7]

x

[0;3]

. Der Betrag des Vektors

|{\vec {P}}-{\vec {LF_{4}}}|

ist der Abstand von Punkt

P

zur Strecke

\epsilon =|TF_{4}|

. Der BBetragberechnet sich im

\mathbb {R} ^{3}

durch:

{\vec {x}}={\begin{pmatrix}x\\y\\z\end{pmatrix}}={\sqrt {x^{2}+y^{2}+z^{2}}}

. Es folgt:

|{\vec {P}}-{\vec {LF_{4}}}|={\sqrt {(P_{x}-LF_{4x})^{2}+(P_{y}-LF_{4y})^{2}+(P_{z}-LF_{4z})^{2}}}

.

Fall 2:

Falls der Lotfußpunkt

LF_{4}

außerhalb des Klassenzimmers

[0;9]\times [0;7]\times [0;3]

liegt, entspricht der im Fall 1 berechnete Abstand zwar dem geringsten Abstand zur Trägergeraden der Strecke, aber nicht dem geringsten Abstand zur eigentlichen Strecke. Ob sich der Lotfußpunkt außerhalb oder innerhalb des Klassenzimmers befindet ist an dessen y-Koordinate zu erkennen, da sich die gesamte Fensterfront auf der Ebene

y=7

befindet. Ist diese größer als 7, so befindet sich der Lotfußpunkt somit nicht mehr im Quader. In diesem Fall berechnet sich der Abstand als Abstand von Punkt

P

zum Schwerpunkt

F_{4}

von Fenster 4, also als

|{\vec {P}}-{\vec {F_{4}}}|={\sqrt {(P_{x}-F_{4x})^{2}+(P_{y}-F_{4y})^{2}+(P_{z}-F_{4z})^{2}}}

Um eine einheitliche Angabe der Lüftungsqualität zu erhalten, mit der sinnvolle Aussagen über optimale und suboptimale Lüftung getroffen werden können, muss der Abstand sinnvoll normiert werden. Hierzu wurde folgende Gleichung gewählt:

L_{4}={1 \over {1+{s_{4}}^{2}}}

Hierbei ist $L_{4}$ die Lüftungsqualität im Bezug zu Fenster 4 und $s_{4}$ der Abstand zu der Lüftungsgeraden von Fenster 4. Die Lüftungsgüte kann durch den Aufbau des Terms nur Werte im Bereich $(0,1]$ annehmen, wobei der Wert eins angenommen wird, falls sich der zu untersuchenden Raumpunkt genau auf der Lüftungsgeraden befindet. Mit immer größer werdendem Abstand konvergiert die Lüftungsqualität gegen Null. Das Quadrieren des Abstandes führt dazu, dass Abständen im Bereich $(0,1)$ um die Schwerpunktgeraden herum kleinere Werte zugeordnet werden. Das ist sinnvoll, da dieser Bereich immer noch sehr stark belüftet wird, was in der ersten Modellüberlegung durch die schiefen Pyramidenstümpfe berücksichtigt wurde.

Die insgesamt Lüftungsgüte $L_{gesamt}\in (0,4]$ errechnet sich schlussendlich als Summe der einzelnen Werte $L_{1}$ bis $L_{4}$ :

L_{gesamt}=L_{1}+L_{2}+L_{3}+L_{4}

Eine Lüftungsgüte von vier bedeutet eine ideale Lüftung.

Umsetzung in GeoGebra[Bearbeiten]

Damit das GeoGebra Applet entsprechend funktioniert und für jeden Raumpunkt eine sinnvolle Lüftungsgüte ermittelt werden kann, muss die Fallunterscheidung sauber eingebaut werden. Hierzu wurden zunächst für jede Lüftungsstrecke zwei Vektoren definiert. Einer, der vom Raumpunkt zum Lotfußpunkt auf der Geraden zeigt und einer, der vom Raumpunkt auf den jeweiligen Fensterschwerpunkt zeigt. Anschließend wird für den zweiten Vektor eine bedingte Sichtbarkeit eingefügt. Hierzu muss ein Wahrheitswert erfragt werden, der angibt, ob der erste Vektor definiert ist, oder nicht. Ist er nicht definiert, wird der zweite Vektor ausgegeben und der erste wird automatisch ausgeblendet. Zur Angabe der Lüftungsgüte im Applet muss der jeweilige verwendete Abstand zu Berechnung über eine "wenn-Abfrage" definiert werden. Wenn der erste Vektor definiert ist, ist der gesuchte Abstand der Betrag des ersten Vektors, ansonsten ist der Abstand der Betrag des zweiten Vektors.

Übersicht der Bezeichnungen in GeoGebra
Fenster	Vektor Luftfußpunkt	Vektor Fensterschwerpunkt	IstDefiniert Vektor Luftfußpunkt	Wenn-Bedingung
2	w₃ Länge: b₅	v₅ Länge: j₅	g₅	k₅
3	v₃ Länge: a₅	w₅ Länge: h₅	f₅	i₅
4	u₃ Länge: c₄	u₅ Länge: p₅	e₅	q₅

Bewertung Modellierungszyklus 2[Bearbeiten]

Weiterhin war das Ziel der Modellierung, die Lüftungsqualität innerhalb eines Klassenzimmers beim Lüften zu untersuchen und Aussagen darüber treffen zu können, wie die Lüftungsqualität im Raum aufgrund des Lüftens ist.

Im zweiten Zyklus ist es möglich, die Luftqualität im Klassenzimmer für jeden möglichen Raumpunkt zu bestimmen. Die im ersten Modellierungszyklus entwickelten Modelle, bei welchen nur eine Ebene des Klassenzimmers betrachtet werden konnte, wurden damit deutlich verbessert. Auch wurde nicht nur der kürzeste Abstand des Punktes zur nächstgelegenen Geraden bestimmt, sondern die Abstände zu allen Geraden im Raum bei der Bewertung der berücksichtigt. Die Aussagekraft des Modells wurde dadurch entscheidend verbessert. Weiterhin wurde davon ausgegangen, dass der Volumenstrom im gesamten Lüftungsverlauf konstant ist. Allerdings muss davon ausgegangen werden, dass der Lüftungsstrom vom Fenster zur Türe zu- oder abnimmt.

Das erste Modell des zweiten Modellierungszyklus hat den Vorteil, dass berücksichtigt wird, dass direkt an den Luftstrom angrenzenden Bereiche besser belüftet sind, als weiter davon entfernte. Allerdings ist dieser Vorteil im Vergleich zu dem erhöhten Rechenaufwand nicht rentabel. Somit stellt das weiterentwickelte Modell, bei welchem Geraden anstelle der Pyramidenstümpfe einen Bezugspunkt für die Luftgüte liefern, ein wesentlich einfacher zu handhabendes Modell dar, ohne, dass das Modell groß an Aussagekraft verliert.

Für eine bestmögliche Verteilung der SuS müsste nun ein Wert festgelegt werden, der nicht von einen möglichen Platz überschritten werden darf. Dieser ist momentan frei wählbar. Eine möglicher Wert wäre die durchschnittliche Luftgüte, allerdings ist diese mit dem hiervorliegendem Modell noch nicht berechenbar.

Optimierung Modellierungszyklus 2[Bearbeiten]

Im zweiten Modellierungszyklus wurde weiterhin angenommen, dass der Volumenstrom zwischen einem Fenster und der Tür gleich bleibt, allerdings ist davon auszugehen, dass vom Fenster zur Tür hin der Strom zu- oder abnimmt. Es können somit nur ungenaue Angaben oder Tendenzen zur Luftqualität an den unterschiedlichen Raumpunkten ermittelt werden.

Auch führt die Vereinfachung, den Luftstrom nur als Geraden darzustellen, dazu, dass für einige Raumpunkte ein verfälschter Wert entsteht. So ist an Punkten, die direkt im Luftstrom liegen, laut diesem Modell eine schlechtere Luftqualität, wenn sie nicht direkt auf der Geraden liegen.

Modellierungszyklus 3 - Niveau Universität[Bearbeiten]

Einführung[Bearbeiten]

Im dritten Modellierungszyklus sollen nun die Modelle des zweiten Modellierungszyklus verbessert werden. Das primäre Ziel ist jetzt nicht mehr, die Luftqualität an einem bestimmten Raumpunkt zu berechnen, sondern aus der berechneten Luftqualität Folgen für die Verteilung von Schülerinnen und Schülern (SuS) im Klassenzimmer und somit über die Anordnung der Sitzplätze im Klassenzimmer treffen zu können. Dafür wird die Luftgüte für jeden beliebigen Raumpunkt als Funktion dargestellt. Um die Funktion noch anschaulich im dreidimensionalen darstellen zu können, wird die Höhe des Klassenzimmers auf einen bestimmten Wert festgelegt (zum Beispiel 1,30 Meter - Also eine klassische Sitzhöhe von SuS der Mittelstufe). Die von der Länge und Breite des Klassenzimmers abhängigen Funktion wird auf das Intervall [0,4] abgebildet. 4 steht hierbei wie im zweiten Modellierungszyklus für die beste Luftqualität, 0 hingegen für die schlechteste. Nachdem festgelegt wurde, wie gut die Luftqualität mindestens an einer Stelle, an der sich SuS befinden, sein muss, kann mit Hilfe der mehrdimensionalen Analysis über das Gradientenaufstiegsverfahren für jeden Ort im Raum entschieden werden, in welche Richtung sich der Sitzplatz eines SuS verschieben müsste, um an einer ausreichend belüfteten Stelle im Klassenzimmer zu sitzen. Mit Hilfe des Computer-Algerba-Systems Maxima kann dies ohne, dass eine graphische Darstellung nötig ist, für jeden Punkt des Klassenzimmers bestimmt werden. Damit nicht mehreren SuS der gleiche Sitzplatz zugeordnet wird und auch noch ein Abstand von 1,5 Metern eingehalten werden kann, wird die Funktion nach der Vergabe eines Sitzplatzes modifiziert, sodass der entsprechende Bereich nicht mehr als einen Sitzplatz für weitere SuS in Frage kommt. Somit kann durch die Bestimmung der Luftqualität an den verschiedenen Punkten im Raum eine praxisrelevante Aussage über die Sitzordnung im Klassenzimmer getroffen werden.

Herleitung der Lüftungsgütefunktion[Bearbeiten]

Die Lüftungsgütefunktion wird nun entsprechend der Vorgehensweise aus Modellierungszyklus 2 aufgestellt. Es werden hier nur die Punkte der Form $P=(p_{1},p_{2},1.3)$ im Raum betrachtet, da in der Praxis vor allem interessant ist, wie gut die Lüftungsqualität auf Kopfhöhe der sitzenden SuS, die auf 1,3 m geschätzt wurde, ist. Die Vorgehensweise bei anderen Höhen ist jedoch vollkommen analog und kann so beliebig auf unterschiedlich große SuS angepasst werden. Analog zu Modellierungszyklus 2 werden vier Geradengleichungen aufgestellt, die die Trägergeraden der Lüftungsstrecken sind. Anschließend werden die Lotfußpunkte des Punktes und der Geraden bestimmt. Der Abstand zwischen den Lotfußpunkten und dem beliebigen Raumpunkt wird ermittelt. Außerdem wird ein Term berechnet, der den Abstand zwischen den Mittelpunkten der Fenster und dem beliebigen Raumpunkt darstellt. Dieser Term wird in dem Fall, dass der Lotfußpunkt außerhalb des Klassenraums liegt verwendet. Die Abstände werden anschließend mithilfe einer Glockenkurve normiert und für jede Lüftungsstrecke addiert

L_{i}={1 \over {1+{s_{i}}^{2}}}

und

L_{ges}=L_{1}+L_{2}+L_{3}+L_{4}

(für eine genauere Erläuterung der Vorgehensweise, siehe Modellierungszyklus 2).

Es folgt eine Fallunterscheidung der Lage der Lotfußpunkte $LF_{2},LF_{3},LF_{4}$ bei der zunächst die verschiedenen Teilfunktionen ermittelt werden.

Falls $LF_{2y}>7$ und $LF_{3y}\leq 7$ und $LF_{4y}\leq 7$ :

i(p_{1},p_{2}):={1 \over {1+{({{\sqrt {100\cdot {p_{2}}^{2}-840\cdot p_{2}+19700\cdot {p_{1}}^{2}-59100\cdot p_{1}+46089}} \over {10\cdot {\sqrt {197}}}})^{2}}}}+{1 \over {1+{({\sqrt {(7-{p_{2}})^{2}+({7 \over 2}-{p_{2}})^{2}+0.039998)^{2}}}}}}+{1 \over {1+{({{\sqrt {1300\cdot {p_{2}}^{2}+(6552-4480)\cdot p_{1}\cdot p_{2}+3940\cdot {p_{1}}^{2}-11916\cdot p_{1}+9477}} \over {6\cdot {\sqrt {145}}}})^{2}}}}+{1 \over {1+{({{\sqrt {2900\cdot {p_{2}}^{2}+(9912-6720)\cdot p_{1}\cdot p_{2}+3940\cdot {p_{1}}^{2}-11964\cdot p_{1}+9693}} \over {2\cdot {\sqrt {1705}}}})^{2}}}}

Falls $LF_{2y}>7$ und $LF_{3y}>7$ und $LF_{4y}\leq 7$ :

j(p_{1},p_{2}):={1 \over {1+{({{\sqrt {100\cdot {p_{2}}^{2}-840\cdot p_{2}+19700\cdot {p_{1}}^{2}-59100\cdot p_{1}+46089}} \over {10\cdot {\sqrt {197}}}})^{2}}}}+{1 \over {1+{({\sqrt {(7-{p_{2}})^{2}+({7 \over 2}-{p_{2}})^{2}+0.039998)^{2}}}}}}+{1 \over {1+{({\sqrt {(11-{p_{2}})^{2}+({11 \over 2}-{p_{2}})^{2}+0.039998)^{2}}}}}}+{1 \over {1+{({{\sqrt {2900\cdot {p_{2}}^{2}+(9912-6720)\cdot p_{1}\cdot p_{2}+3940\cdot {p_{1}}^{2}-11964\cdot p_{1}+9693}} \over {2\cdot {\sqrt {1705}}}})^{2}}}}

Falls $LF_{2y}\leq 7$ und $LF_{3y}>7$ und $LF_{4y}\leq 7$ :

k(p_{1},p_{2}):={1 \over {1+{({{\sqrt {100\cdot {p_{2}}^{2}-840\cdot p_{2}+19700\cdot {p_{1}}^{2}-59100\cdot p_{1}+46089}} \over {10\cdot {\sqrt {197}}}})^{2}}}}+{1 \over {1+{({{\sqrt {1700\cdot {p_{2}}^{2}+(15960-11200)\cdot p_{1}\cdot p_{2}+19700\cdot {p_{1}}^{2}-59340\cdot p_{1}+46593}} \over {10\cdot {\sqrt {213}}}})^{2}}}}+{1 \over {1+{({\sqrt {(11-{p_{2}})^{2}+({11 \over 2}-{p_{2}})^{2}+0.039998)^{2}}}}}}+{1 \over {1+{({{\sqrt {2900\cdot {p_{2}}^{2}+(9912-6720)\cdot p_{1}\cdot p_{2}+3940\cdot {p_{1}}^{2}-11964\cdot p_{1}+9693}} \over {2\cdot {\sqrt {1705}}}})^{2}}}}

Falls $LF_{2y}>7$ und $LF_{3y}>7$ und $LF_{4y}>7$ :

l(p_{1},p_{2}):={1 \over {1+{({{\sqrt {100\cdot {p_{2}}^{2}-840\cdot p_{2}+19700\cdot {p_{1}}^{2}-59100\cdot p_{1}+46089}} \over {10\cdot {\sqrt {197}}}})^{2}}}}+{1 \over {1+{({\sqrt {(7-{p_{2}})^{2}+({7 \over 2}-{p_{2}})^{2}+0.039998)^{2}}}}}}+{1 \over {1+{({\sqrt {(11-{p_{2}})^{2}+({11 \over 2}-{p_{2}})^{2}+0.039998)^{2}}}}}}+{1 \over {1+{({\sqrt {(15-{p_{2}})^{2}+({15 \over 2}-{p_{2}})^{2}+0.039998)^{2}}}}}}

Falls $LF_{2y}\leq 7$ und $L_{3y}\leq 7$ und $LF_{4y}\leq 7$ :

f(p_{1},p_{2}):={1 \over {1+{({{\sqrt {100\cdot {p_{2}}^{2}-840\cdot p_{2}+19700\cdot {p_{1}}^{2}-59100\cdot p_{1}+46089}} \over {10\cdot {\sqrt {197}}}})^{2}}}}+{1 \over {1+{({{\sqrt {1700\cdot {p_{2}}^{2}+(15960-11200)\cdot p_{1}\cdot p_{2}+19700\cdot {p_{1}}^{2}-59340\cdot p_{1}+46593}} \over {10\cdot {\sqrt {213}}}})^{2}}}}+{1 \over {1+{({{\sqrt {1300\cdot {p_{2}}^{2}+(6552-4480)\cdot p_{1}\cdot p_{2}+3940\cdot {p_{1}}^{2}-11916\cdot p_{1}+9477}} \over {6\cdot {\sqrt {145}}}})^{2}}}}+{1 \over {1+{({{\sqrt {2900\cdot {p_{2}}^{2}+(9912-6720)\cdot p_{1}\cdot p_{2}+3940\cdot {p_{1}}^{2}-11964\cdot p_{1}+9693}} \over {2\cdot {\sqrt {1705}}}})^{2}}}}

Die verschiedene Teilfunktionen werden anschließend zu einer Gesamtlüftungsgütefunktion $n$ zusammengesetzt:

$n:[0,9]\times [0,7]\to \mathbb {R} ,n(p_{1},p_{2})={\begin{cases}i(p_{1},p_{2})&LF_{2y}>7&{\text{und}}&LF_{3y},LF_{4y}\leq 7\\j(p_{1},p_{2})&LF_{2y},LF_{3y}>7&{\text{und}}&LF_{4y}\leq 7\\k(p_{1},p_{2})&LF_{2y}\leq 7&{\text{und}}&LF_{3y}>7&{\text{und}}&LF_{4y}\leq 7\\l(p_{1},p_{2})&LF_{2y},LF_{3y},LF_{4y}>7\\f(p_{1},p_{2})&{\text{sonst}}&\end{cases}}$

In dem Computer Algebra System Maxima wurde die Funktion über eine if-Bedingung definiert.

(%i33)n(p_1,p_2):=if(LF_2(p_1,p_2)[2]>7 and LF_3(p_1,p_2)[2]≤7 and LF_4(p_1,p_2)[2]≤7)then(i(p_1,p_2))
          else if(LF_2(p_1,p_2)[2]>7 and LF_3(p_1,p_2)[2]>7 and LF_4(p_1,p_2)[2]≤7)then(j(p_1,p_2))
          else if(LF_2(p_1,p_2)[2]≤7 and LF_3(p_1,p_2)[2]>7 and LF_4(p_1,p_2)[2]≤7)then(k(p_1,p_2))
          else if(LF_2(p_1,p_2)[2]>7 and LF_3(p_1,p_2)[2]>7 and LF_4(p_1,p_2)[2]>7)then(l(p_1,p_2))
      else(f(p_1,p_2));;

(%o33)n(p₁,p₂):=if [LF₂]₂>7 and [LF₃]₂≤7 and [LF₄]₂≤7) then i(p₁,p₂)
          else if [LF₂]₂>7 and [LF₃]₂>7 and [LF₄]₂≤7) then j(p₁,p₂)
          else if [LF₂]₂≤7 and [LF₃]₂>7 and [LF₄]₂≤7) then k(p₁,p₂)
          else if [LF₂]₂>7 and [LF₃]₂>7 and [LF₄]₂>7) then l(p₁,p₂)
      else f(p₁,p₂)

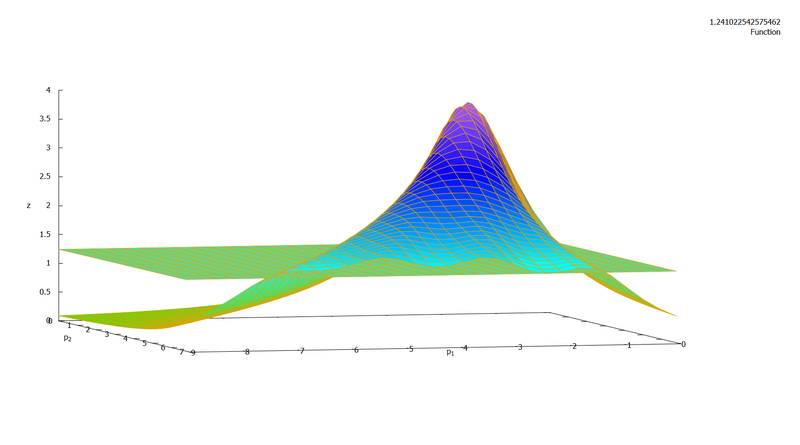
Wird die Lüftungsgütefunktion im Bereich $[0,9]\times [0,7]$ und der Höhe 1,3 geplottet, ist deutlichh zu erkennen, wo die Lüftungsgüte im Raum hoch und wo sie niedrig ist. Das Maximum erreicht die Funktion dort, wo sich die Tür befindet.

Plot der Lüftungsgütefunktion n auf der Höhe 1,3

Da die Funktion durch die Fallunterscheidung für das Programm Maxima nicht integriert oder abgeleitet werden kann, wird die im Folgenden die Funktion f als Näherung der Lüftungsgütefunktion verwendet. Die Funktion f entspricht der Lüftungsgütefunktion, wenn zur Berechnung des Abstandes zu den Lüftungsgeraden nur das Lotfußpunktverfahren genutzt wird. Der Unterschied zwischen Funktion f und n ist bei einer Höhe von 1,3 sehr gering. So ist $f(8.8,6.3)\approx 0.4603$ und $n(8.8,6.3)\approx 0.4432$ . Der Unterschied ist in einem Plot beider Funktionen in einem Koordinatensystem nur Minimal zu sehen. Für die Anwendung dieses Modells in der Praxis ist dieser Unterschied vernachlässigbar.

Vergleich der Funktionen f und n (n ist die untere Funktion, f ist die obere Funktion)

Bestimmung des Mittelwertes[Bearbeiten]

Nachdem nun die Funktion für eine feste, für den Sachverhalt sinnvolle Höhe geplottet wurde, hat man einen guten Überblick erlangt, in welchen Bereichen die Luftqualität hoch und in welchen Bereichen sie niedrig ist. Bei der reinen Betrachtung der $p_{1}$ - $p_{2}$ - Ebene sind hier auch viele Übereinstimmungen mit dem Modell des ersten Modellierungszyklus' zu erkennen.

Berechnung des Integrals der Luftgüte-Funktion mit Maxima:

{\begin{aligned}&{\mathtt {\color {Apricot}\%i32}}&&{\mathtt {{\color {green}y{\underline {\ }}1}:\ {\color {brown}integrate}{\color {blue}(}{\color {brown}f}{\color {blue}(}{\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2}{\color {blue})},{\color {green}p{\underline {\ }}1},{\color {brown}0},{\color {brown}9}{\color {blue})};}}\\&{}&&{\color {red}{\text{Is}}\ 25p_{2}^{2}-210p_{2}+5366\ {\text{positive or negative?}}}\ \color {green}{\text{positive}};\\&{\mathtt {\color {orange}(y{\underline {\ }}1)}}&&{\Bigg (}5{\sqrt {341}}\operatorname {atan} \left({\frac {\left(1680{\sqrt {341}}p_{2}+2991{\sqrt {341}}\right){\sqrt {25p_{2}^{2}-210p_{2}+5366}}}{17050p_{2}^{2}-143220p_{2}+3659612}}\right)\\&{}&&+5{\sqrt {213}}\operatorname {atan} \left({\frac {\left(560{\sqrt {213}}p_{2}+2967{\sqrt {213}}\right){\sqrt {25p_{2}^{2}-210p_{2}+5366}}}{10650p_{2}^{2}-89460p_{2}+2285916}}\right)\\&{}&&+15{\sqrt {29}}\operatorname {atan} \left({\frac {\left(1120{\sqrt {29}}p_{2}+2979{\sqrt {29}}\right){\sqrt {25p_{2}^{2}-210p_{2}+5366}}}{4350p_{2}^{2}-36540p_{2}+933684}}\right)\\&{}&&+5{\sqrt {179}}\operatorname {atan} \left({\frac {15{\sqrt {179}}p_{2}{\sqrt {25p_{2}^{2}-210p_{2}+5366}}}{50p_{2}^{2}-420p_{2}+10732}}\right)\\&{}&&{\Bigg )}/{\sqrt {25p_{2}^{2}-210p_{2}+5366}}\\&{}&&-{\Bigg (}5{\sqrt {341}}\operatorname {atan} \left({\frac {\left(1680{\sqrt {341}}p_{2}-14739{\sqrt {341}}\right){\sqrt {25p_{2}^{2}-210p_{2}+5366}}}{17050p_{2}^{2}-143220p_{2}+3659612}}\right)\\&{}&&+5{\sqrt {213}}\operatorname {atan} \left({\frac {\left(560{\sqrt {213}}p_{2}-14763{\sqrt {213}}\right){\sqrt {25p_{2}^{2}-210p_{2}+5366}}}{10650p_{2}^{2}-89460p_{2}+2285916}}\right)\\&{}&&+15{\sqrt {29}}\operatorname {atan} \left({\frac {\left(1120{\sqrt {29}}p_{2}-14751{\sqrt {29}}\right){\sqrt {25p_{2}^{2}-210p_{2}+5366}}}{4350p_{2}^{2}-36540p_{2}+933684}}\right)\\&{}&&-5{\sqrt {179}}\operatorname {atan} \left({\frac {15{\sqrt {179}}p_{2}{\sqrt {25p_{2}^{2}-210p_{2}+5366}}}{50p_{2}^{2}-420p_{2}+10732}}\right)\\&{}&&{\Bigg )}/{\sqrt {25p_{2}^{2}-210p_{2}+5366}}\\&{\mathtt {\color {Apricot}\%i33}}&&{\mathtt {{\color {green}I}:\ {\color {brown}romberg}{\color {blue}((}{\color {green}y{\underline {\ }}1}{\color {blue})},{\color {green}p{\underline {\ }}2},{\color {brown}0},{\color {brown}7}{\color {blue})};}}\\&{\mathtt {\color {orange}(I)}}&&78.18442018225412\end{aligned}}

Nun gilt es einen vernünftigen Wert, sozusagen eine Unterschranke, der Luftgüte festzulegen, in dessen Bereich die SuS hingesetzt werden sollen. Diesen Wert könnte man reintheoretisch frei wählen, allerdings war die Idee, den Mittelwert der Luftgüte zu berechnen und diesen als Mindestwert zu definieren. Dieser Mittelwert entspricht dem Volumen der Funktion geteilt durch die Grundfläche des Klassenzimmers. Dieses wird wie folgt berechnet:

zuerst nach $p_{1}$ über $[0,9]$ integrieren, dann nach $p_{2}$ über $[0,7]$ : $I=\int _{0}^{7}\int _{0}^{9}f(p_{1},p_{2})\ dp_{2}dp_{1}=78,18$
dann $I_{2}={I \over {7\cdot 9}}={78,18 \over {63}}=1,24$

Da die Integration sehr aufwendig ist, wurde dafür das Computeralgebrasystem Maxima benutzt. Zur Lösung dieses Integrals wurde der Satz von Fubini angewandt. Dieser besagt, dass man in einem mehrdimensionalen Integral die Integrationen nacheinander ausführen kann, wenn die Grenzen unabhängig von den zu integrierenden Variablen sind. Nach der ersten Integration nach einer Variablen, entsteht aus dem mehrdimensionalen Integral ein eindimensionales, welches leicht als Riemann-Integral gelöst werden kann. Hierzu lässt sich sagen, dass für die Integration nach $p_{1}$ der Befehl "integrate" verwendet wurde, für die Integration nach $p_{2}$ dann der Befehl "romberg", der das Integral numerisch berechnet, da Maxima nicht in der Lage war, das Integral über eine Stammfunktion genau zu berechnen (siehe auch Bild: Berechnung des Integrals der Luftgüte-Funktion mit Maxima). Lässt man sich die Luftgüte-Funktion zusammen mit der Ebene $I_{2}$ plotten, kann man nun gut den Bereich erkennen, in dem die Luftqualität durch Lüften so hoch ist, dass man hier SuS hinsetzen kann.

Wie positioniere ich die Schüler? - Gradientenaufstiegsverfahren[Bearbeiten]

Gradienten Bestimmung durch Maxima Teil 1

{\begin{aligned}&{\mathtt {{\color {green}g{\underline {\ }}1}:{\color {brown}diff}({\color {brown}f}({\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2}),{\color {green}p{\underline {\ }}1},{\color {brown}1});}}\\\\&-{\frac {-6720p_{2}+7880p_{1}-11964}{6820\left({\frac {2900p_{2}^{2}+(9912-6720p_{1})p_{2}+3940p_{1}^{2}-11964p_{1}+9693}{6820}}+1\right)^{2}}}\\&-{\frac {-11200p_{2}+39400p_{1}-59340}{21300\left({\frac {1700p_{2}^{2}+(15960-11200p_{1})p_{2}+19700p_{1}^{2}-59340p_{1}+46593}{21300}}+1\right)^{2}}}\\&-{\frac {-4480p_{2}+7880p_{1}-11916}{5220\left({\frac {1300p_{2}^{2}+(6552-4480p_{1})p_{2}+3940p_{1}^{2}-11916p_{1}+9477}{5220}}+1\right)^{2}}}\\&-{\frac {39400p_{1}-59100}{19700\left({\frac {100p_{2}^{2}+840p_{2}+19700p_{1}^{2}-59100p_{1}+46089}{19700}}+1\right)^{2}}}\end{aligned}}

Gradienten Bestimmung durch Maxima Teil 2

{\begin{aligned}&{\mathtt {{\color {brown}g}({\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2}):=[{\color {brown}g{\underline {\ }}1}({\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2}),{\color {brown}g{\underline {\ }}2}({\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2})];}}\\&g(p_{1},p_{2}):=[g_{1}(p_{1},p_{2}),g_{2}(p_{1},p_{2})]\end{aligned}}

Gradientenabstiegsverfahren durch Maxima

x: 9;
9

y: 5;
5

S: [x,y];
[9,5]

if(f(S[1],S[2])<I_2)
then(S: float((g(S[1],S[2] ·1/(sqrt(g(S[1],S[2]).g(S[1],S[2]))))+[S[1],S[2]]))
else(print("Punkt erreicht"), print(S));
Punkt erreicht
[6.58013094730602,6.772900652427504]
[6.58013094730602,6.772900652427504]

Das Gradientenaufstiegsverfahren ist eine mathematische Methode in mehrdimensionalen Räumen.

In unserem Beispiel behandeln wir eine Funktion $f$ des Typs $f(p_{1},p_{2})\colon \ [0,9]\times [0,7]\to \mathbb {R}$ .

Es wird von einem Punkt $S=(x,y)$ der Gradient bestimmt: $grad(x,y)=g(x,y)=({\frac {\partial f(x,y)}{\partial p_{1}}},{\frac {\partial f(x,y)}{\partial p_{2}}})$ . Dieser zeigt in die Richtung des steilsten Anstiegs am Punkt $S=(x,y)$ .

Der Gradient wird normiert, sodass der Betrag des Gradienten $|({\tilde {g}}(x,y))|=1$ ist.

Der normierte Gradient wird zu $S=(x,y)$ addiert: $S'=(x',y')={\tilde {g}}(x,y)+(x,y)=(({\frac {\partial f(x,y)}{\partial p_{1}}})^{2}+({\frac {\partial f(x,y)}{\partial p_{2}}})^{2})^{-1/2}\cdot g(x,y)+(x,y)$

Der Punkt $S'=(x',y')$ sollte einen höheren Funktionswert haben als der Punkt $S=(x,y)$ . Falls dies nicht der Fall ist, muss die Schrittlänge verringert werden (zB durch $0,1$ ): $S'=(x',y')=0,1\cdot (({\frac {\partial f(x,y)}{\partial p_{1}}})^{2}+({\frac {\partial f(x,y)}{\partial p_{2}}})^{2})^{-1/2}\cdot g(x,y)+(x,y)$

Der Punkt $S=(x,y)$ an dem sich der/die Schüler/in befindet, soll so verschoben werden, dass der Funktionswert $f(x',y')$ größer als die mittlere Lüftungsgüte $I_{2}=1,241$ ist. Hierzu wird das Gradientenaufstiegsverfahren so lange hintereinander durchgeführt, bis die neue Position $(x',y')$ des/der Schülers/in über der durchschnittlichen Lüftungsgüte liegt.

Einfluss besetzter Plätze - Theorie[Bearbeiten]

Mit dem "Gradientenaufstiegsverfahren" könnte nun allerdings nur ein Schüler im Raum verteilt werden, denn bereits verteilte Plätze dürfen nicht mehr vergeben werden und zusätzlich sollte auch der Bereich um den Platz herum gemieden werden (1,5m Sicherheitsabstand). Dem soll entgegengewirkt werden, indem die Luftgüte an bereits verteilten Plätzen heruntergesetzt wird, sozusagen eine "Delle" in der Funktion entsteht und dieser Platz dann durch das Gradientenaufstiegsverfahren nicht mehr erreicht wird. Dies wurde wie folgt modelliert:

Die Luftgüte-Funktion muss mit folgendem Term addiert werden: ${{(I_{2}-f(S[1],S[2])-0.5)} \over {(1+{{(p_{1}-S[1])^{2}+(p_{2}-S[2])^{2}} \over {0.5^{2}}}})}$ wobei $S$ den bereits vergebenen Platz, $S[1]$ die $p_{1}$ -Koordinate und $S[2]$ die $p_{2}$ -Koordinate von $S$ beschreibt. Dieser abzuziehende Term ist sehr ähnlich zu den vier einzelnen Termen der Luftgüte-Funktion aufgebaut. Er wurde so konstruiert, dass am Punkt $S$ eine Delle entsteht. Da dieser Platz nun vergeben ist, soll die Luftgüte dort in einem kleines Kreis mit Mittelpunkt $S$ unter den Referenzwert $I_{2}$ gesetzt werden. Daher wurde der Zähler als $(I_{2}-f(S[1],S[2])-0.5)$ gewählt. Dadurch landet man für jeden Punkt $S$ um 0,5 unter dem Referenzwert $I_{2}$ . Durch das Teilen mit $0.5^{2}$ wird die Kuhle breiter gemacht, sodass der Sicherheitsabstand gewahrt wird.

Der Einfluss der verschiedenen Parameter wurden in der nebenstehenden GeoGebra-Datei in einer zweidimensionalen Funktion veranschaulicht.

Damit entsteht folgende neue Funktion: $f_{2}(p_{1},p_{2})=f(p_{1},p_{2})+{{(I_{2}-f(S[1],S[2])-0.5)} \over {(1+{{(p_{1}-S[1])^{2}+(p_{2}-S[2])^{2}} \over {0.5^{2}}}})}$ Diese wurde zur Veranschaulichung mit Maxima für den Punkt $S=(2|1)$ geplottet.

Diese kann nun wieder für das Gradientenaufstiegsverfahren benutzt werden, denn dort, wo der erste Schüler nun sitzt, ist ein lokales Minima entstanden und der Gradient wird dadurch nicht mehr dorthin führen.

Bewertung[Bearbeiten]

Im Vergleich zu den ersten beiden Modellierungszyklen lag beim dritten Modellierungszyklus ein erweitertes Ziel vor: Im Vordergrund stand nicht mehr allgemein die Bestimmung der Luftqualität, sondern die Schlüsse, die man aus der berechneten Luftqualität ziehen kann. Das Modell liefert eine sehr gute Möglichkeit, Aussagen darüber treffen zu können, wie SuS im Klassenzimmer unter Berücksichtigung der Luftqualität und des Abstandes platziert werden sollten. Somit erzielt das Modell seinen Zweck. Optimierungsmöglichkeiten des zweiten Zyklus konnten durch die Verlagerung des Schwerpunkts auf die Praktische Anwendung im dritten Zyklus nicht ausgebaut werden. So wurde der Volumenstrom im Klassenzimmer weiterhin als konstant angesehen, was aber durch die Modellannahmen eine akzeptable Vereinfachung ist.

Trotz der großen Aussagekraft des Modells weißt es auch ein paar Schwächen auf: So kann die Platzierung der SuS immer nur für eine gegebene Höhe bestimmt werden. In der Beispielrechnung wurde das für eine Höhe von 1,30 Meter durchgeführt, da das eine durchschnittliche Höhe des Kopfes eines Mittelstufenschülers beim Sitzen ist. Allerdings gibt es gerade bei Kindern und Jugendlichen, die die Schule besuchen, Unterschiede in der Körpergröße und damit auch in der Höhe verschiedener SuS beim Sitzen. So kann nur eine optimale Anordnung der Sitzplätze für eine Durchschnittsgröße der SuS, die die Klasse besuchen, berechnet werden, auch wenn diese Sitzordnung dann nicht für alle SuS tatsächlich optimal ist.

Ein weiterer negativer Aspekt des Modells ist es, dass ein Zahlenwert für die Luftqualität gewählt werden muss, sodass in Bereichen mit einer niedrigeren Luftgüte keine SuS platziert werden dürfen. In der Beispielrechnung wurde das über die mittleren Luftqualität des Raums festgelegt. Ob dieser Mittelwert dann tatsächlich ein gutes Maß für die Grenze der Platzierung ist ist in Frage zu stellen.

Optimierung[Bearbeiten]

Um den dritten Modellierungszyklus zu optimieren können die Optimierungen des zweiten Modellierungszyklus - der zur Berechnung der Funktion genutzt werde - im dritten Zyklus berücksichtigt werden. Zudem ist das Gradientenanstiegsverfahren zwar ein gutes Verfahren, um Sitzplätze der SuS an Stellen im Klassenzimmer zu bewegen, es kann aber sehr aufwendig sein. Grund dafür ist, dass die Sitzplätze entlang eines Vektors bewegt werden, der auf die Länge 1 normiert wurde. Befindet sich ein Sitzplatz an einem Ort, der von dem Bereich, in dem die Luftqualität gut genug zum Sitzen ist, weit entfernt ist, so muss das Gradientenaufstiegsverfahren mehrfach angewendet werden, bis dieser Sitzplatz an einem Ort mit guter Luftqualität verschoben wurde. Durch die Veränderung der Länge dieses Vektors, könnte das Verfahren beschleunigt werden. Allerdings darf die Länge dieses Vektors auch nicht zu groß sein, da der Sitzplatz durch verschieben nicht in, sondern wieder außerhalb des gut belüfteten Bereichs landen könnte, nur auf der anderen Seite des gut belüfteten Bereichs. Wie genau die Länge des Vektors im Optimalfall gewählt werden müsste, könnte in einem weiteren Optimierungsprozesses ermittelt werden. Außerdem könnten Daten erhoben werden, um das bisher auf Annahmen basierte Modell zu überprüfen und zu verifizieren.

Modellierungszyklus 4 - Implementierung in Comsol 2D[Bearbeiten]

Theoretische Grundlagen[Bearbeiten]

Rampe

Zur realitischeren Darstellung der Einströmgeschwindigkeit wurde eine Rampe verwendet, die dafür sorgt, dass die maximale Einströmgeschwindigkeit erst nach circa $0,3s$ erreicht wird. Hierfür wurde eine geglättete Rampe mit der Steigung $5$ gewählt, siehe Abbildung 0.

Randbedingungen

An allen Wänden liegen Dirichlet-Randbedingungen, auch Haftbedingungen genannt, vor, d.h. an ihnen beträgt die Geschwindigkeit $u=0$ . Am Auslass (Tür) wurde eine Neumann-Randbedingung gewählt mit Normalspannung $f_{0}=0$ . Am Einlass ist eine parabolische Einlassfunktion (siehe unten) vorgegeben.

Lösungsverfahren

Comsol löst die Simulation mit algebraischen Mehrgitterverfahren auf der Basis des impliziten Eulerverfahrens.

Modellierungsprozess[Bearbeiten]

Die Maße des allgemeinen Aufbaus des Klassenzimmers wurden vom vorherigen Modellierungsprozess übernommen. Hinzugefügt wurden Tischoberflächen und die Köpfe der Personen in Form von rechteckigen und kreisförmigen Flächen. Einen Einfluss auf den Luftstrom haben jedoch nur die kreisförmigen Flächen, da der betrachtete Ebenenquerschnitt auf Höhe der Köpfe der Personen festgelegt wurde. Grund hierfür ist, dass auf Kopfhöhe die Ausströmung der Aerosole stattfindet. Eine Darstellung des konstruierten Raumes ist in Abbildung 1 dargestellt. Der einströmende Luftstrom wurde mittels parabolischer Gleichung für jedes Fenster separat festgelegt. Diese lautet für das Fenster unten links wie folgt: ${-16\cdot u_{max}\cdot rm1(t)\cdot (y-1)\cdot (y-2)}$

wobei für $u_{max}=2,5{m \over s}=9{km \over h}$ und die Rampe mit Steigung 5 gewählt wurde.

Des Weiteren wurden an die Kreisflächen Ellipsen angefügt, die die Münder bzw. Nasen der jeweiligen Person darstellen sollen. Dies ist in Abbildung 2 dargestellt. Diese Ellipse dient außerhalb des für den Kopf dargestellten Kreis als Einlass für die Ausatemluft der einzelnen Personen. Dies geschieht mit $u_{aus}=0,83{m \over s}=2,988{km \over h}$ , was mit ungefähr $3{km \over h}$ der durchschnittlichen Atemgeschwindigkeit eines Menschen entspricht.

Modellierungsergebnis[Bearbeiten]

In Abbildung 3 wird die modellierte Luftstromgeschwindigkeit dargestellt, die sich durch Berechnung mit Comsol durch die oben angegebene Formel ergibt. Hierbei ist zu beachten, dass die Geschwindigkeit bei allen 4 Fenstern gleich gesetzt wurde und wir lediglich den Ausfluss an der Tür gegeben haben.

In diese Modellierung des gelüfteten Klassenzimmer lassen sich nun noch Partikel integrieren, die den Ausstoß von Aerosolen darstellen sollen. Dabei befinden sich bei den farblich rot markierten Partikel Krankheitserreger unter den Aerosolen, bei den grünen Partikeln handelt es sich um unbedenkliche Aerosole. Dies ist beispielhaft im nachfolgenden GIF (Abbildung 4) mit zwei infizierten Personen dargestellt.

Mittels der Modellierung kann nun nachverfolgt werden, wie mögliche Wege der Krankheitserreger verlaufen und welche Positionen im Raum infizierte Personen einnehmen müssen, um möglichst viele bzw. möglichst wenige andere Personen anzustecken. Dies soll in der nachfolgenden Tabelle dargestellt werden. Die Bezeichnung in der ersten Spalte beschreibt die Position der Person im Klassenzimmer und ist hierbei wie folgt aufgebaut: lR3.4 bezeichnet links in der dritten Reihe den vierten Platz.

Position der infizierten Personen	Modellierung	Position möglicher neuinfizierter Personen
Lehrkraft		Betroffen sein könnten gegebenenfalls Personen mit Position rR1.3, rR1.4 und danach gegebenenfalls auch Personen mit Postion rR2.3 und rR2.4. Das Ansteckungsrisiko wäre somit hier als hoch einzustufen.
lR1.4		Betroffen wären Personen mit Position rR1.2, rR2.1, rR2.2, rR3.2, rR3.3 und rR3.4. Das Ansteckungsrisiko wäre somit hier als sehr hoch einzustufen.
rR1.4		Betroffen wären in diesem Fall keine Person direkt, ein geringes Risiko könnte für Personen mit Position rR2.4 und rR3.4 gegeben sein. Das Ansteckungsrisiko wäre somit hier als niedrig einzustufen.
rR1.1		Betroffen wären Personen mit Position rR2.3, rR2.4 und rR3.4. Das Ansteckungsrisiko wäre somit hier als hoch einzustufen.
lR1.1		Betroffen wären Personen mit Position rR1.1, rR1.2, rR2.2 und rR2.3. Gegebenenfalls bestünde für Personen mit Position rR3.4 ebenfalls ein erhöhtes Risiko. Das Ansteckungsrisiko wäre somit hier als hoch einzustufen.
lR3.4/ lR4.4/ rR3.4		Es gibt keine Position mit erhöhtem Risiko. Das Ansteckungsrisiko wäre somit hier als sehr niedrig einzustufen.

Fazit[Bearbeiten]

Die Analyse der verschiedenen in der Tabelle dargestellten Fälle zeigt, dass eine Person, die an einer über Aerosole übertragbaren Krankheit infiziert ist, möglichst im hinteren Bereich des Klassenzimmers platziert werden sollte. Eine Platzierung nahe der Fenster oder an Randplätzen der einzelnen Reihen stellt im Allgemeinen noch keine Garantie der geringsten Ansteckung dar. Im hinteren Bereich des Klassenzimmers sind die infizierten Personen bestmöglich in direkter Nähe zur Türe oder im direkten Luftstrom zur Türe aufgehoben, sodass eine Verbreitung der Krankheit auf andere Personen möglichst gering gehalten wird. Dennoch ist es selbstverständlich immer zu empfehlen, im Krankheitsfall zu Hause zu bleiben. Des Weiteren wäre Personen, welche beispielsweise aufgrund der Zugehörigkeit zu einer Risikogruppe in keinem Fall erkranken sollten, zu raten, sich im linken Bereich des Klassenzimmers zu platzieren, da hier die geringste Wahrscheinlichkeit einer Ansteckung gegeben ist.

Diese Aussagen treffen auf eine Situation zu, in welcher das Klassenzimmer wie in diesem Modell aufgebaut ist.

Optimierungsmöglichkeiten[Bearbeiten]

Neben den bisher betrachteten an unterschiedlichen Orten erkrankten Personen könnte des Weiteren auch verschiedene Lüftungsprozesse betrachtet werden. In diesem Modell wird bisher davon ausgegangen, dass alle vier Fenster gleichzeitig vollständig geöffnet sind. Diese Annahme wurde aufgrund der Theorie des Stoßlüftens getroffen. Jedoch ist es in einem Klassenzimmer durchaus auch möglich, dass auch nur einzelne Fenster vollständig oder auch nur gekippt geöffnet sind. Diese Szenarien könnten zu einer weiteren Risikobewertung zusätzlich noch betrachtet werden. Weiterhin atmen die Personen in diesem Raum lediglich aus. Eine Optimierung wäre hier, an jeder Ellipse neben einem Einlass auch einen Auslass mit einer bestimmten Geschwindigkeit zu platzieren, die das Einatmen der Personen darstellen soll. Des Weiteren atmen alle Personen durchgängig aus und verteilen die Partikel immer zur gleichen Zeit. Hier wäre eine Optimierungsmöglichkeit, dass das Ausatmen immer nach einem bestimmten Zeitschritt passiert und auch, dass die Personen zu unterschiedliche Zeitpunkten atmen. Dies wäre vor allem auch dann sinnvoll, wenn die Optimierung mit dem Einatmen durchgeführt werden soll, da sonst die Möglichkeit besteht, dass die Personen direkt ihre ausgeatmeten Partikel wieder einatmen. In diesem Modellierungszyklus wurde die Annahme getroffen, dass sich die Köpfe der Personen alle auf einer Ebene befinden und somit alle Personen sitzend gleich groß sind und sich zudem nicht bewegen. Dies entspricht nicht der Realität, ist aber notwendig, um erst eine allgemeine Aussage treffen zu können. Diese Annahme lässt sich aber auch auf konkrete Beispiele anpassen.

Die eben betrachtete Simulation stellt das Klassenzimmer im zweidimensionalen Raum dar. Die Stömungslinien der Luft können entsprechend auch nur in der dargestellten Ebene verlaufen. Innerhalb eines realen dreidimensionalen Klassenzimmers verläuft der Luftstrom allerdings nicht nur im Rahmen einer Ebene, sondern im gesamten Raum. Dies führt entsprechend zu Verwirbelungen und anders verlaufenden Strömungslinien als im zweidimensionalen Raum. Das hier dargestellte Modell ermöglicht zwar eine grobe Risikoabschätzung, ist aber ungenauer als eine Modellierung im dreidimensionalen. Entsprechend wird im nächsten Modellierungszyklus das Klassenzimmer als dreidimensionaler Raum betrachtet, um eine realitätsgetreuere Risikoabschätzung vornehmen zu können.

Modellierungszyklus 5 - Implementierung in Comsol 3D[Bearbeiten]

Modellierungsprozess[Bearbeiten]

Die Maße des allgemeinen Aufbaus des Klassenzimmers wurden vom vorherigen Modellierungsprozess übernommen. Als weiterer Parameter wurde die Hohe des Klassenzimmers mit berücksichtigt und wie im Geogebra-Modell gewählt. Hinzugefügt wurden Tische und die Köpfe und Körper der Personen in Form von Quadern, Kugeln und Ellipsoide. Zur Vereinfachung wurden die eigentlich auf Stühlen sitzenden Körper als Ellipsoid dargestellt. Weiterhin wurde vereinfacht angenommen, dass alle Personen im Raum gleich groß sind (1,35m). Der einströmende Luftstrom wurde mittels parabolischer Gleichung für jedes Fenster separat festgelegt. Diese lautet für das Fenster gegenüber der Tür wie folgt: ${-16\cdot u_{max}\cdot rm1(t)\cdot ((x-1)\cdot (x-2)+(z-1)\cdot (z-2))}$

Modellierungsergebnis[Bearbeiten]

In Abbildung 5 wird das dreidimensional modellierte Klassenzimmer dargestellt. Die Maße entsprechen dem des zweidimensionalen Modells. Die Höhe des Raums, der Fenster, der Türe und der Tische wurden wahrheitsgetreu angepasst. Gleiches gilt auch für die Höhe der Köpfe der Personen.

In Abbildung 6 wird die modellierte Luftstromgeschwindigkeit dargestellt, die sich durch Berechnung mit Comsol durch die oben angegebene Formel ergibt. Hierbei ist zu beachten, dass die Geschwindigkeit bei allen 4 Fenstern gleich gesetzt wurde und wir lediglich den Ausfluss an der Tür gegeben haben. In diese Modellierung des gelüfteten Klassenzimmer lassen sich nun noch Partikel integrieren, die den Ausstoß von Aerosolen darstellen sollen. Dabei befinden sich bei den farblich rot markierten Partikel Krankheitserreger unter den Aerosolen, bei den grünen Partikeln handelt es sich um unbedenkliche Aerosole. Dies ist beispielhaft im nachfolgenden GIF (Abbildung 6) dargestellt.

Mittels der Modellierung kann nun nachverfolgt werden, wie mögliche Wege der Krankheitserreger verlaufen und welche Positionen im Raum infizierte Personen einnehmen müssen, um möglichst viele bzw. möglichst wenige andere Personen anzustecken. Dies soll in der nachfolgenden Tabelle dargestellt werden. Die Bezeichnung in der ersten Spalte beschreibt wie zuvor bereits erläutert die Position der Person im Klassenzimmer. Im Gegensatz zum zweidimensionalen Modell ist die der Zeitpunkt, welcher in der nachfolgenden Tabelle betrachtet wird, bereits nach einer Sekunde. Im zweidimensionalen Modell ist die Endaufnahme nach 2 Sekunden zu sehen. Dieser Unterschied ergibt sich aus der erhöhten Berechnungslaufzeit für das dreidimensionale Modell.

Position der infizierten Personen	Modellierung 3dim	Position möglicher neuinfizierter Personen 3dim
Lehrkraft		Das Bild des Endzustandes erlaubt keine konkrete Vorhersage und auch keine Vermutung.
lR1.4		Das Bild des Endzustandes erlaubt keine konkrete Vorhersage. Vermutet werden kann allerdings, dass Personen mit Position lR2.4, rR1.1, rR1.2, rR2.1 und rR2.2 einem höheren Risiko ausgesetzt sind.
rR1.4		Das Bild des Endzustandes erlaubt keine konkrete Vorhersage. Vermutet werden kann allerdings, dass Personen mit Position rR2.4 und rR3.4 einem höheren Risiko ausgesetzt sind.
rR1.1		Das Bild des Endzustandes erlaubt keine konkrete Vorhersage. Vermutet werden kann allerdings, dass Personen mit Position rR2.3 und rR2.4, sowie gegebenenfalls in der Reihe dahinter einem höheren Risiko ausgesetzt sind.
lR1.1		Das Bild des Endzustandes erlaubt keine konkrete Vorhersage. Vermutet werden kann allerdings, dass Personen mit Position lR2.4, sowie die Personen mit Positionen in der rechen Reihe 2 und 3 einem höheren Risiko ausgesetzt sind.
lR3.4/ lR4.4/ rR3.4		Das Bild erlaubt auch eher eine Vermutung, dennoch ist stark davon auszugehen, dass Personen mit dieser Position kein erhöhtes Risiko für andere Personen aufweisen.

In Abbildung 7 wird der Klassenraum in seitlicher Perspektive gezeigt. Hierauf ist zu sehen, dass sich die Partikel nicht konstant auf der Höhe der Köpfe der Personen bewegen, sondern auch in höhere oder tiefere Ebenen. Entsprechend werden diese gegebenenfalls nicht wie erwartet eingeatmet und stellen hiermit ein geringeres Risiko dar. Leider kann hierüber keine genauere Aussage getroffen werden, da das Modell aufgrund der Berechnungszeit nur die Partikelbewegung den Zustand nach maximal einer Sekunde anzeigen kann.

Fazit[Bearbeiten]

Der Rechenaufwand ist aufgrund der Anzahl der iterativen Schritte im dreidimensionalen Modell derart hoch, dass der Zeitaufwand der Berechnung in keinem Verhältnis zum Mehrwert der Erkenntnis durch die räumliche Darstellung steht. So konnten der Modellverlauf aufgrund der fehlenden technischen Gegebenheiten nur im zeitlichen Rahmen einer Sekunde betrachtet werden. Somit ist eine Risikobewertung nicht wirklich möglich gewesen. Entsprechend ist für die Risikobewertung das zweidimensionale Modell trotz der höheren Fehleranfälligkeit aussagekräftiger.

Optimierungsmöglichkeiten[Bearbeiten]

Neben den bisher betrachteten an unterschiedlichen Orten erkrankten Personen könnte des Weiteren auch verschiedene Lüftungsprozesse betrachtet werden. In diesem Modell wird bisher davon ausgegangen, dass alle vier Fenster gleichzeitig vollständig geöffnet sind. Diese Annahme wurde aufgrund der Theorie des Stoßlüftens getroffen. Jedoch ist es in einem Klassenzimmer durchaus auch möglich, dass auch nur einzelne Fenster vollständig oder auch nur gekippt geöffnet sind. Diese Szenarien könnten zu einer weiteren Risikobewertung zusätzlich noch betrachtet werden. Des Weiteren würde eine längere Laufzeit die Aussagekraft des Modells erhöhen. Dies wäre mit dem erarbeiteten Programm durchaus möglich, allerdings sind dafür entsprechende technische Gegebenheiten notwendig, sodass die Berechnung nicht mehrere Tage andauert.

Teilprojekt 2[Bearbeiten]

Modellierungszyklus 1[Bearbeiten]

Beispiel-Unternehmen gründen[Bearbeiten]

Um mit der eigentlichen Modellierung zu beginnen, mussten als erstes Einnahmen, Ausgaben, Gewinn- und Kostendeckungsgrad für 5 Unternehmen ausgelotet werden. Dazu wurde zuerst ein Beispiel-Unternehmen gegründet und die Werte bezüglich der Einnahmen und Ausgaben möglichst genau recherchiert und dann gegenübergestellt. Im Falle unseres Beispiel-Unternehmens handelt es sich um eine Pizzeria, welche auf dem Rathausplatz in der Landauer Innenstadt ansässig ist und welcher insgesamt eine Geschäfts-Fläche von 300m² zur Verfügung stehen. Die Öffnungszeiten des Restaurants sind Dienstag bis Sonntag von 11:00 Uhr bis 23:00 Uhr. In der Zeit vor dem ersten Lockdown setzen sich die Einnahmen und Ausgaben wie folgt zusammen:

Einnahmen und Ausgaben eines italienischen Restaurants *vor Corona*
(Standort: Landau, Rathausplatz)
Einnahmen			Ausgaben
E1	Restaurant	79.500,00 €	A1	Miete/Pacht	4.000,00 €
E2	Lieferservice	0,00 €	A2	Grundgebühr	23,00 €
E3	Abholservice	8.745,00 €	A3	Telefon & Internet	25,00 €
			A4	GEZ	23,00 €
			A5	Versicherung (inkl. KFZ)	250,00 €
			A6	Müllentsorgung	330,00 €
			A7	Krankenversicherung	700,00 €
			A8	Strom	1.700,00 €
			A9	Wasser	320,00 €
			A10	Abwasser	225,00 €
			A11	Heizung (Gas)	300,00 €
			A12	Gas	50,00 €
			A13	Gehälter	19.736,00 €
			A14	Werbung	200,00 €
			A15	Einkäufe/Warenkosten	20.073,75 €
			A16	Gewerbesteuer	3.511,67 €
			A17	Steuer	13.265,00 €
			A18	Ausstattung	200,00 €
			A19	Fahrer	0,00 €
			A20	Liefe-Autos (Leasing)	0,00 €
			A21	Hygiene	0,00 €
			A22	Rücklagen	5.000,00 €
	Einnahmen	88.245,00 €		Ausgaben	69.932,42 €
	Gewinn	18.312,58 €		Kostendeckungsgrad	126,19 %

Die Einnahmen (pro Monat) setzen sich aus folgenden Positionen zusammen:

Restaurant: 150 Gäste pro Tag, 20€ je Gast, multipliziert mit 26,5 Tage pro Monat (30,5 Tage pro Monat abzüglich eines freien Tages pro Woche)
Lieferservice: wird zu diesem Zeitpunkt nicht angeboten.
Abholservice: 30 Gäste pro Tag, 11€ je Gast, multipliziert mit 26,5 Tage pro Monat

Die Ausgaben (pro Monat) setzen sich aus folgenden Positionen zusammen:

4.000€ Miete für 300m²
Grundgebühr für Strom, Gas und Wasser
Vertrag für Internet und Telefon
Rundfunkbeiträge für Gewerbe
Versicherungen inkl. Autoversicherung
Müllentsorgungskosten
Krankenversicherung
Verbrauch für Strom, Wasser (inkl. sanitärer Anlagen), Abwasser, (Gas-)Heizung, Gas (Herd)
Gehälter der Festangestellten + Lohnnebenkosten (Faktor 1,18): 2 Köche à 2500€/Person, 3 Küchenhilfen und 3 Service-Kräfte à 1700€/Person, 4 Minijobber auf 450€-Basis, Inhaber hilft beschränkt im Service mit
geringe Werbung, um Abholservice und Speisekarte zu bewerben
Die Einkäufe und Warenkosten richten sich nach den Einnahmen.
- Einnahmen im Restaurant: 150*20*26,5 (Einnahmen pro Person 20€ (14€ für Speisen und 6€ für Getränke), 150 Gäste pro Tag und 26,5 Tage im Monat)
- Einnahmen Abholservice: 30*11*26,5 (11€ Einnahmen pro Person, 30 Gäste pro Tag und 26,5 Tage im Monat)
- Warenkosten für die Speisen: (14*150*26,5)/4 (14€ pro Person, 150 Gäste pro Tag und 26,5 Tage im Monat, Division durch 4 um die Warenkosten zu erhalten)
- Warenkosten für die Getränke: (6*150*26,5)/6 (6€ pro Person, 150 Gästen pro Tag und 26,5 Tage im Monat , Division durch 6 um die Warenkosten zu erhalten)
- Abholservice analog: (11*30*26,5)/4 (11€ pro Person, 30 Personen pro Tag und 26,5 Tage im Monat, Division durch 4 um die Warenkosten zu erhalten).
Die Gewerbesteuer, und Einkommenssteuer richten sich jeweils nach den Einnahmen des Gewerbes (Verwendung eines Gewerbesteuerrechners)
Ausstattung inklusive Erneuerungen
Rücklagen

Während des ersten Lockdowns verschärft sich die Lage für die Gastronomie.

Einnahmen und Ausgaben eines italienischen Restaurants *während des 1. Lockdowns*
(Standort: Landau, Rathausplatz)
Einnahmen			Ausgaben
E1	Restaurant	0,00 €	A1	Miete/Pacht	4.000,00 €
E2	Lieferservice	19.080,00 €	A2	Grundgebühr	23,00 €
E3	Abholservice	17.490,00 €	A3	Telefon & Internet	25,00 €
			A4	GEZ	23,00 €
			A5	Versicherung (inkl. KFZ)	350,00 €
			A6	Müllentsorgung	330,00 €
			A7	Krankenversicherung	700,00 €
			A8	Strom	1.700,00 €
			A9	Wasser	320,00 €
			A10	Abwasser	225,00 €
			A11	Heizung (Gas)	300,00 €
			A12	Gas	50,00 €
			A13	Gehälter	9.912,00 €
			A14	Werbung	1.000,00 €
			A15	Einkäufe/Warenkosten	9.823,93 €
			A16	Gewerbesteuer	3.511,67 €
			A17	Steuer	2.392,43,00 €
			A18	Ausstattung	500,00 €
			A19	Fahrer	900,00 €
			A20	Liefer-Autos (Leasing)	300,00 €
			A21	Hygiene	50,00 €
			A22	Rücklagen	5.000,00 €
	Einnahmen	36.570,00 €		Ausgaben	41.436,03 €
	Gewinn	-4.866,03 €		Kostendeckungsgrad	88,26 %

Die Einnahmen ändern sich wie folgt:

Einnahmen im Restaurant: 0€ (Das Restaurant muss coronabedingt schließen)
Einnahmen durch den neu eingeführten Lieferservice: 60*12*26,5 (60 Portionen pro Tag, 12€ pro Portion und 26,5 Tagen pro Monat).
Einnahmen durch Abholservice: 60*11*26,5 (60 Personen pro Tag, 11€ pro Portion und 26,5 Tage pro Monat)

Die Ausgaben verändern sich auf den folgenden Positionen:

Veränderung für
- Versicherungen auf 350€, da fortan zwei PKW als Liefer-Fahrzeuge versichert werden müssen.
- Festangestellte (2 Köche à 2500€/Person, 2 Küchenhilfen, Inhaber hilft aktiv mit)
- Werbung (steigt, da nun Lieferservice und Abholservice intensiv beworben werden)
- Einkäufe, Warenkosten und Mehrwertsteuer (Anpassung an Einnahmen, sinken entsprechend)
- Kosten der Ausstattung (Anstieg aufgrund zusätzlicher Besorgungen)
Keine Veränderung für
- Kosten für Strom, Wasser, Gas (Bezahlung im Voraus)
- Gewerbesteuer (pauschal einmal im Jahr bezahlt)
Zusätzliche Kosten:
- Zwei Fahrer auf je 450€-Basis
- Zwei Fahrzeuge werden für je 50€ im Monat geleast.
- Für Hygiene (z. B. Desinfektionsmittel-Spender) müssen zusätzlich Aufwendungen betrieben werden.

Nach dem ersten Lockdown entspannt sich die Lage zunächst. Restaurants dürfen teilweise wieder öffnen.

Einnahmen und Ausgaben eines italienischen Restaurants *nach dem 1. Lockdown*
(Standort: Landau, Rathausplatz)
Einnahmen			Ausgaben
E1	Restaurant	26.500,00 €	A1	Miete/Pacht	4.000,00 €
E2	Lieferservice	12.720,00 €	A2	Grundgebühr	23,00 €
E3	Abholservice	11.660,00 €	A3	Telefon & Internet	25,00 €
			A4	GEZ	23,00 €
			A5	Versicherung (inkl. KFZ)	350,00 €
			A6	Müllentsorgung	330,00 €
			A7	Krankenversicherung	700,00 €
			A8	Strom	1.700,00 €
			A9	Wasser	320,00 €
			A10	Abwasser	225,00 €
			A11	Heizung (Gas)	300,00 €
			A12	Gas	50,00 €
			A13	Gehälter	14.374,00 €
			A14	Werbung	600,00 €
			A15	Einkäufe/Warenkosten	12.511,79 €
			A16	Gewerbesteuer	3.511,67 €
			A17	Steuer	4.816,12 €
			A18	Ausstattung	700,00 €
			A19	Fahrer	900,00 €
			A20	Liefer-Autos (Leasing)	300,00 €
			A21	Hygiene	150,00 €
			A22	Rücklagen	5.000,00 €
	Einnahmen	50.880,00 €		Ausgaben	50.909,57 €
	Gewinn	-29,57 €		Kostendeckungsgrad	99,94 %

Die Einnahmen verändern sich wie folgt:

Restaurant: 50*20*26,5 (Restaurant darf aufgrund der Corona-Maßnahmen nicht jeden Platz besetzen, 50 Gäste pro Tag)
Liefer- und Abholservice mit je 40 Portionen bzw. Gästen am Tag bleiben beide bestehen.

Die Ausgaben verändern sich wie folgt:

Personal: 2 Köche à 2500€/Person, 2 Küchenhilfen und 2 Service-Kräfte à 1700€/Person, 450€ Reinigungskraft, Inhaber hilft weiterhin mit.
weniger Werbung betrieben werden, aber weitaus mehr als vor des ersten Lockdowns.
Einkäufe, Warenkosten sowie die Mehrwertsteuer steigen (Anpassung an Einnahmen)
Kosten für Ausstattung und Hygiene steigen, da coronabedingt Maßnahmen ergriffen werden müssen

Gewinn-Berechnung[Bearbeiten]

Für die Gewinnberechnung müssen vorerst die Einnahmen und Ausgaben berechnet werden. Dies haben wir für unsere 5 Beispielunternehmen ermittelt (vgl. Abb. 4).

Der Gewinn lässt sich im Allgemeinen wie folgt berechnen:

${\text{E:= Einnahmen}}$

${\text{A:= Ausgaben (Kosten)}}$

${\text{G:= Gewinn}}$

Mit Hilfe der Gleichung $G=E-A$ wurde der Gewinn für jedes unserer Beispielunternehmen berechnet (vgl. Abb. 4).

Beispiel: Unternehmen 1

${\text{E= 88.245 €}}$

${\text{A = 69.932,42 €}}$

${\text{G = E – A = 88.245 € - 69.932,42 € = 18.312,58 €}}$

Das Tabellenkalkulationsprogramm LibreOffice Calc diente dazu, den Gewinn unserer 5 Beispielunternehmen untereinander zu vergleichen.

Kostendeckungsgrad[Bearbeiten]

Der Kostendeckungsgrad beschreibt das Verhältnis der Einnahmen zu den Ausgaben (Kosten).

Dieser lässt sich wie folgt bestimmen:

${\text{Kostendeckungsgrad}}={\frac {E}{A}}$

Mit Hilfe der obigen Gleichung konnte der Kostendeckungsgrad der 5 Unternehmen berechnet werden (vgl. Abb. 4).

Beispiel: Unternehmen 1

${\text{Kostendeckungsgrad}}={\frac {88.245}{69.932,42}}={\text{126,19}}$ %

Der Kostendeckungsgrad wird prozentual angegeben. Somit kann folgendes geschlussfolgert werden:

Wenn der Kostendeckungsgrad 100% beträgt, können alle Ausgaben vollständig durch die Einnahmen gedeckt werden.
Falls der Kostendeckungsgrad <100%, macht das Unternehmen Verluste.
Falls der Kostendeckungsgrad >100% werden Gewinne erzielt.
In unserem Beispiel (vgl. Abb. 4) haben alle Unternehmen vor Corona Gewinn gemacht.

Tabellenkalkulation der fünf Unternehmen[Bearbeiten]

Einnahmen-/Ausgabenkalkulation der fünf Unternehmen
		Unternehmen 1	Unternehmen 2	Unternehmen 3	Unternehmen 4	Unternehmen 5	Durchschnitt
Vor Corona	Einnahmen	88.245,00 €	26.500,00 €	18.000,00 €	127.200,00 €	57.637,50 €	63.516,50 €
	Ausgaben	69.912,42 €	20.239,00 €	13.355,00 €	102.245,00 €	43.163,04 €	49.786,89 €
	Gewinn	18.312,58 €	6.261,00 €	4.645,00 €	24.955,00 €	14.474,46 €	13.729,61 €
	Kostendeckung	126,19 %	130,94 %	134,78 %	124,41 %	133,53 %	129,97 %
Während 1. Lockdowns	Einnahmen	36.570,00 €	21.200,00 €	3.360,00 €	12,000,00 €	25.970,00 €	19.820,00 €
	Ausgaben	41.436,03 €	18.867,00 €	6.791,00 €	34.816,00 €	25.967,79 €	25.575,56 €
	Gewinn	-4.866,03 €	2.333,00 €	-3.431,00 €	-22.816,00 €	2,21 €	-5.755,56 €
	Kostendeckung	88,26 %	112,37 %	49,48 %	34,47 %	100,01 %	76,91 %
Nach 1. Lockdown	Einnahmen	50.880,00 €	25.175,00 €	12.800,00 €	84.800,00 €	39.750,00 €	42.681,00 €
	Ausgaben	50.909,57 €	19.572,75 €	10.956,00 €	77.306,33 €	30.927,93 €	37.934,52 €
	Gewinn	-29,57 €	5.602,25 €	1.844,00 €	7.493,67 €	8.822,07 €	4.746,48 €
	Kostendeckung	99,94 %	128,62 %	116,83 %	109,69 %	128,52 %	116,72 %
45.000,00 € staatliche Mittel (für drei Monate)		9.000,00 €	9.000,00 €	9.000,00 €	9.000,00 €	9.000,00 €	9.000,00 €
15.000,00 € staatliche Mittel (für einen Monat)		3.000,00 €	3.000,00 €	3.000,00 €	3.000,00 €	3.000,00 €	3.000,00 €
Gewinn inklusive staatlicher Mittel		-1.866,03 €	5.333,00 €	-431,00 €	-19.816,00 €	3.002,21 €	-2.755,56 €

Die ausführlich aufgestellte Gewinn- und Kostenaufstellung für unser Beispiel-Unternehmen vor Corona, während des 1. Lockdowns und nach dem Lockdown wurden nun, zur besseren Vergleichbarkeit, jeweils auf den Aspekt der Einnahmen, der Ausgaben, des Gewinnes und des Kostendeckungsgrads beschränkt. Zudem wurden Gewinn- und Kostaufstellungen für vier weitere Unternehmen, ebenfalls vor Corona, während des 1. Lockdowns und nach dem Lockdown, erstellt, denen jeweils unterschiedliche Parameter zugrunde liegen.

Bei unserem Unternehmen 2 handelt es sich um einen kleinen Imbiss, der nur Speisen und Getränke zum Mitnehmen verkauft und keine Sitzgelegenheiten anbietet. Dementsprechend ist die Ladenfläche deutlich geringer, was eine deutlich geringere Miete zur Folge hat. Zusätzlich benötigt er weniger Personal und legt nicht so hohen Wert auf hochwertige Produkte, sodass zum einen die Warenkosten günstiger sind, zum anderen aber auch die Speisen günstiger verkauft werden können. Somit hat der Imbiss geringere Fixkosten und Nebenkosten, aber auch geringere Einnahmen. Während des 1. Lockdowns sanken die Einnahmen, da weniger Laufkundschaft bedient werden konnte. Um dem entgegenzuwirken wurde ein zusätzlicher Lieferdienst eingeführt. Dieser erhöhte zwar die Fix- und Nebenkosten, führte aber auch dazu, dass der Einnahmeverlust deutlich geringer ausfiel. Trotz des Lockdowns macht der Imbiss Gewinn. Nach dem 1. Lockdown wurde der Lieferdienst beibehalten, es kam aber auch wieder mehr Laufkundschaft, sodass der Gewinn ähnlich hoch ausfällt wie vor der Corona-Pandemie.

Bei unserem Unternehmen 3 handelt es sich um eine Weinstube in Nußdorf, die von einer Winzerfamilie geführt wird. Dadurch muss das Unternehmen kaum Gehälter und auch keine Miete zahlen, dementsprechend gering fallen die Fixkosten, aber auch die Nebenkosten, aus. Während des 1. Lockdowns wurden nur noch zweimal in der Woche Speisen zum Mitnehmen angeboten, weshalb die Einnahmen drastisch sanken. Nach dem Lockdown wurde der Essensverkauf zum Mitnehmen wieder eingestellt und nur das Restaurant geöffnet, da aber aufgrund der Abstands- und Hygieneregeln weniger Kunden bewirtet werden können, werden trotzdem weniger Einnahmen generiert.

Bei unserem Unternehmen 4 handelt es sich um ein Sterne-Restaurant. Das Restaurant ist sehr groß, sodass die Miete sehr hoch ausfällt, zudem benötigt es einen großen Personalaufwand und die Zutaten sind aufgrund der hohen Qualität sehr teuer, sodass das Sterne-Restaurant sehr hohe Fix- und Nebenkosten besitzt. Da die Getränke und Speisen allerdings ebenfalls relativ teuer sind und die Kunden viel Geld dort für eine Mahlzeit ausgeben, sind auch die Einnahmen sehr hoch. Während des 1. Lockdowns wurde zwar ein Abholservice eingerichtet, der aber nicht sehr erfolgreich war, sodass die Einnahmen sehr stark sanken. Auch wenn die Nebenkosten deutlich gesenkt werden konnten, weil große Teile des Personal in Kurzarbeit gingen und deutlich weniger Lebensmittel verbraucht wurden, waren die Fixkosten nach wie vor, vor allem durch die Miete, sehr hoch, sodass das Unternehmen große Verluste einfahren musste. Nach dem Lockdown normalisierte sich die Lage wieder und der Abholservice wurde wieder eingestellt. Doch aufgrund der Abstands- und Hygieneregeln konnten weniger Kunden bewirten werden und somit auch weniger Einnahmen generiert werden.

Bei unserem Unternehmen 5 handelt es sich um ein eher kleines Restaurant mit deutlich weniger Personal und deutlich weniger Fläche, sodass die Fix- und Nebenkosten deutlich geringer ausfallen, zudem besitzt das Restaurant schon seit einiger Zeit einen Abholservice. Während des 1. Lockdowns wurde der bereits etablierte Abholservice ausgebaut und durch einen Lieferdienst ergänzt, dadurch war es möglich die Einnahmen weiterhin relativ hochzuhalten. Da gleichzeitig ein großer Teil des Personals in Kurzarbeit geschickt werden konnte, verringerten sich die Nebenkosten relativ stark, sodass sie trotz des Lockdowns zumindest keine Verluste beklagen mussten. Nach dem Lockdown blieb der Abhol- und Lieferservice weiterhin erhalten, aber auch das Restaurant konnte wieder öffnen, allerdings aufgrund der geltenden Abstands- und Hygieneregeln mit deutlich verminderter Kundenanzahl.

Berechnung des arithmetischen Mittels[Bearbeiten]

Um die durchschnittlichen Einnahmen, Ausgaben sowie den Gewinn und den Kostendeckungsgrad der fünf Unternehmen (n=5) zu bestimmen wurde jeweils das arithmetische Mittel berechnet.

Allgemein gilt:

{\overline {x}}:={\frac {1}{n}}(x_{1}+x_{2}+\ldots +x_{n})={\frac {1}{n}}\sum _{i=1}^{n}{x_{i}}

^[5]

Für unser Modell ergibt sich beispielsweise für die Einnahmen vor Corona:

{\overline {x}}={\frac {88245+26500+18000+127200+57637,5}{5}}=63516{,}5

€

Dies wird sowohl für die Zeit vor Corona, als auch für die Zeit während des 1. Lockdowns und für die Zeit nach dem Lockdown durchgeführt.

Gleiche Verteilung der staatlichen Mittel auf alle Unternehmen[Bearbeiten]

In der Zeit während des ersten Lockdowns beschließt das Bundesfinanzministerium Soforthilfen in Höhe von 9000€ für drei Monate pro Unternehmen. Dies soll den möglichen Einnahmeverlusten entgegenwirken. Folglich erhält jedes unserer Beispielunternehmen die gleiche monatliche Förderung von 3000€ (siehe Abb. 4). Trotzdem können nach der Auszahlung der Soforthilfen nur Unternehmen 2 und 5 ihre laufenden Kosten während des Lockdowns vollständig decken beziehungsweise ihren zuvor schon positiven Gewinn erhöhen. Alle anderen Unternehmen haben dagegen nach wie vor Verluste zu beklagen. Insbesondere Unternehmen 4 liegt trotz der finanziellen Unterstützung des Staats noch weit unterhalb des Nullpunkts.

Säulendiagramm des Kostendeckungsgrades[Bearbeiten]

In Abb. 5 werden die zuvor errechneten Kostendeckungsgrade der fünf Beispielunternehmen zu den drei Zeitpunkten vor der Pandemie, sowie während und nach dem 1. Lockdown in einem Säulendiagramm dargestellt. Zur besseren Übersicht wurde eine Gerade bei y = 100 (%) eingezeichnet, die den finanziellen Nullpunkt angibt. Oberhalb dieser Geraden werden alle Kosten durch die Einnahmen gedeckt. Im Zeitraum vor der Pandemie lässt sich durch das Diagramm gut erkennen, dass alle Unternehmen positive Gewinne erzielten und damit auch alle laufenden Kosten abdecken konnten. Zu Beginn des 1. Lockdowns musste die Gastronomie dann aber für den Publikumsverkehr vollständig schließen, sodass lediglich die Möglichkeit eines Abhol- beziehungsweise Lieferservices blieb. Für Restaurants, die vorher schon verstärkt Abhol- und/ oder Lieferservice angeboten hatten, wie beispielsweise der Imbiss (Unternehmen 2), brach der Gewinn zwar ein, die laufenden Kosten konnten aber noch ausreichend gedeckt werden. Die Pizzeria (Unternehmen 1), die Weinstube (Unternehmen 3) und das Sternerestaurant (Unternehmen 4) verzeichneten aber durch den Lockdown einen starken Einbruch der Einnahmen und damit auch des Kostendeckungsgrades, da ihre betrieblichen Strukturen vollständig auf den Publikumsverkehr ausgerichtet sind. Alle drei Unternehmen können ihre laufenden Kosten nicht mehr tragen und benötigen schnellstmögliche Unterstützung oder die Erlaubnis der Wiedereröffnung. Nach dem ersten Lockdown durften Mahlzeiten auch wieder in den Restaurants verkauft werden. Das Ganze durfte aber nur unter diversen Einschränkungen, wie zum Beispiel Abstandsvorgaben der Tische, stattfinden. Dadurch konnten die Restaurants im Vergleich zu der Zeit vor der Pandemie nicht die maximalen Gewinne erzielen. Es reichte jedoch aus, dass 4 von 5 Unternehmen ihre Kosten decken und größtenteils wieder ansehnliche Gewinne erzielen konnten.

Bewertung 1[Bearbeiten]

Das Ziel unseres Modells ist es, die staatlichen Zuschüsse an unsere fünf Beispielunternehmen gerecht zu verteilen. Im 1. Modellierungszyklus haben wir die staatlichen Zuschüsse (zu einem Betrag x = 15.000€) in gleicher Höhe an unsere Beispielunternehmen verteilt. Dadurch erhielt jedes Unternehmen 3.000€ (Rechnung: 15.000€ / 5 = 3.000€) an staatlichen Zuschüssen pro Monat. Im Allgemeinen hat sich der Gewinn jedes Unternehmens erhöht, wobei die Beispielunternehmen 1, 3 und 4 weiterhin nur Verluste verzeichnen können. Außerdem zeigt sich insgesamt, dass der Gewinn während des Lockdowns mit staatlichen Zuschüssen bei vielen Unternehmen stark vom Gewinn vor Corona abweicht (Vgl. Abb. 6). Wir erhalten eine durchschnittliche Abweichung von 16.485,17€.

Durchschnittliche Abweichung = |Gewinn vor Corona im Durchschnitt – (Gewinn während des Lockdowns mit staatlichen Zuschüssen im Durchschnitt) |

Optimierung 1[Bearbeiten]

Das Ziel ist es, die durchschnittliche Abweichung so gering wie möglich zu halten. Aufgrund der starken durchschnittlichen Abweichung des Gewinns vor Corona, sollte die Verteilung der staatlichen Mittel von den Umsätzen in der Zeit vor dem ersten Lockdown abhängig sein. Wir vermuten dadurch eine geringere Abweichung.

[Somit werden die unterschiedlichen Einnahmen und Ausgaben der jeweiligen Unternehmen berücksichtigt.]

Modellierungszyklus 2[Bearbeiten]

Lineare Funktionen[Bearbeiten]

Allgemein gilt:

$f(x)=n+m\cdot x$

n: Gewinn während des Lockdowns

m: Umsatz vor Corona

x: staatlichen Zuschüsse in Prozent

Funktionsgraphen[Bearbeiten]

Funktionsgraph von Unternehmen 1: $f(x)=-4866+0,01*x*88245$

Funktionsgraph von Unternehmen 2: $g(x)=2333+0,01*x*26500$

Funktionsgraph von Unternehmen 3: $h(x)=-3431+0,01*x*18000$

Funktionsgraph von Unternehmen 4: $i(x)=-22816+0,01*x*127200$

Funktionsgraph von Unternehmen 5: $j(x)=2,21+0,01*x*57637$

(Siehe Abb.7)

Schieberegler[Bearbeiten]

Die Gerade des Schiebereglers a ist parallel zur y-Achse. Dieser Schieberegler soll den prozentualen Anteil der staatlichen Zuschüsse darstellen. Dementsprechend reichen die Werte des Schieberegels von 0 bis 100.

Die Gerade des Schiebereglers b ist parallel zur x-Achse. Dies soll den Gewinn vor Corona visualisieren. Hier reichen die Werte des Schiebereglers vom niedrigsten Gewinn vor Corona der Unternehmen bis zum höchsten Gewinn vor Corona der Unternehmen, d. h. von 4000 bis 25000.

Lagebeziehung[Bearbeiten]

Das Ziel ist es den prozentualen Anteil der Zuschüsse graphisch zu ermitteln. Dabei sollen die Unternehmen mit Hilfe der staatlichen Zuschüsse den gleichen Gewinn wie vor Corona erwirtschaften können. Wir sind wie folgt vorgegangen: Für jedes Unternehmen haben wir den Schiebregler b auf den Wert des Gewinns vor Corona eingestellt. Dann haben wir den Schnittpunkt von b mit dem Funktionsgraph bestimmt. Die x-Koordinate des Schnittpunkts bestimmt den prozentualen Anteil der Zuschüsse, d. h. der Schnittpunkt gibt Auskunft darüber, wie hoch der prozentuale Anteil der staatlichen Zuschüsse sein muss, um den Gewinn vor Corona zu erlangen. Mit Hilfe des Schiebereglers a kann der prozentuale Anteil der Zuschüsse visualisiert werden.

Staatliche Zuschüsse[Bearbeiten]

Abb. 8: Staatliche Zuschüsse Zyklus 2
	Unternehmen 1	Unternehmen 2	Unternehmen 3	Unternehmen 4	Unternehmen 5	Durchschnitt
Staatliche Zuschüsse (%)	26,27 %	18,82 %	44,87 %	37,56 %	25,11 %	29,73 %

Abschließend haben wir die x-Koordinaten der jeweiligen Schnittpunkte bestimmt und den prozentualen Anteil der Zuschüsse tabellarisch zusammengestellt. Der Durchschnitt dieser Anteile ergibt unsere neue Verteilung der staatliche Zuschüsse. Demnach bekommt jedes Unternehmen ca. 30% des Umsatzes vor Corona (siehe Abb.8).

Vektorgleichungen[Bearbeiten]

Das Optimierungsziel dieses Zyklus besteht darin die Verteilung der staatlichen Mittel in Abhängigkeit von den Umsätzen in der Zeit vor dem ersten Lockdown zu betrachten. Alternativ zu der obigen graphischen Vorgehensweise über lineare Funktionen gibt es (auf Oberstufenniveau) auch die Möglichkeit, eine Gerade mit Hilfe der Vektorrechnung ^[6] zu beschreiben und damit das Problem auch rechnerisch zu lösen. Jede Gerade g lässt sich durch eine Gleichung der Form $g:{\vec {x}}={\vec {p}}+t\,{\vec {r}}$ ( $t\in \mathbb {R}$ ) beschreiben. Diese Darstellungsform nennt sich Parameterform ^[7] einer Geraden.

Der Ortsvektor ${\overrightarrow {OP}}$ eines Punktes $P=(p_{1},p_{2})$ , der auf der Geraden liegt, wird, üblicherweise mit ${\vec {p}}={\tbinom {p_{1}}{p_{2}}}\in \mathbb {R} ^{2}$ bezeichnet. Man nennt diesen Vektor auch Stützvektor der Geraden. Der Vektor ${\vec {r}}$ nennt sich Richtungsvektor. Er ist der Differenzvektor (Verbindungsvektor) zu einem beliebigen weiteren Punkt der Geraden. Eine Gerade besteht also aus denjenigen Punkten in der Ebene, deren Ortsvektoren ${\vec {x}}$ die Gleichung der Parameterform erfüllen. Da der Parameter $t\in \mathbb {R}$ ist erhält man letztendlich alle Punkte der Geraden g.

Aus Abb. 4 können die jeweiligen Ortsvektoren ${\vec {o}}_{1},...,{\vec {o}}_{5}\in \mathbb {R} ^{2}$ der fünf Unternehmen der Umsatzgeraden $u_{1},...,u_{5}$ leicht bestimmt werden, da man dort die Punkte $P_{1},...,P_{5}$ (Gewinn während des 1. Lockdowns ohne staatliche Zuschüsse) herauslesen kann. Als Richtungsvektoren ${\vec {r}}_{1},...,{\vec {r}}_{5}\in \mathbb {R} ^{2}$ werden die jeweiligen Umsätze vor Corona mit 100% staatlicher Zuschüsse betrachtet. Aus den Stützvektoren ${\vec {o}}_{1},...,{\vec {o}}_{5}\in \mathbb {R} ^{2}$ und den Richtungsvektoren ${\vec {r}}_{1},...,{\vec {r}}_{5}\in \mathbb {R} ^{2}$ lassen sich nun die Gleichungen der Umsatzgeraden der Unternehmen $u_{1},...,u_{5}$ in Parameterform in Abhängigkeit von $t\in \mathbb {R}$ aufstellen.

Unternehmen 1:

u_{1}:{\vec {x}}={\tbinom {0}{-4866}}+t\,{\tbinom {100}{88245}}

mit

t\in \mathbb {R}

Unternehmen 2:

u_{2}:{\vec {x}}={\tbinom {0}{2333}}+t\,{\tbinom {100}{26500}}

mit

t\in \mathbb {R}

Unternehmen 3:

u_{3}:{\vec {x}}={\tbinom {0}{-3431}}+t\,{\tbinom {100}{18000}}

mit

t\in \mathbb {R}

Unternehmen 4:

u_{4}:{\vec {x}}={\tbinom {0}{-22816}}+t\,{\tbinom {100}{127200}}

mit

t\in \mathbb {R}

Unternehmen 5:

u_{5}:{\vec {x}}={\tbinom {0}{2.21}}+t\,{\tbinom {100}{57637}}

mit

t\in \mathbb {R}

Ziel ist es, die jeweiligen staatlichen Zuschüsse als prozentualen Anteil des jeweiligen Umsatzes vor Corona für jedes Unternehmen zu ermitteln. Das bedeutet hier in unserem Modell, dass wir die $x_{1}$ -Komponenten der jeweiligen Gleichungen der Umsatzgeraden berechnen müssen. Die $x_{2}$ -Komponenten geben den jeweiligen angestrebten Gewinn $G$ vor Corona an und ist somit bekannt. Um die gesuchten $x_{1}$ -Komponenten zu ermitteln, setzt man den Ortsvektor ${\vec {x}}={\tbinom {x_{1}}{G}}$ in die dazugehörige Parametergleichung der Umsatzgeraden $u_{1},...,u_{5}$ ein. Daraus ergeben sich zwei Gleichungen, die zuerst nach $t$ und danach nach $x_{1}$ umgestellt wird. Dadurch erhält man für jede Umsatzgerade $u_{1},...,u_{5}$ die gesuchte $x_{1}$ -Komponente und hat damit den jeweiligen staatlichen Zuschuss als prozentualen Anteil des jeweiligen Umsatzes vor Corona für jedes Unternehmen berechnet.

Beispielrechnung zu Unternehmen 1:

Es gilt:

u_{1}:{\vec {x}}={\tbinom {0}{-4866}}+t\,{\tbinom {100}{88245}}

mit

t\in \mathbb {R}

und

{\vec {x}}={\tbinom {x_{1}}{18312}}

1. Setze ${\vec {x}}={\tbinom {x_{1}}{18312}}$ in die Parametergleichung von $u_{1}$ ein

Daraus ergibt sich folgende Gleichung:

{\tbinom {x_{1}}{18312}}={\tbinom {0}{-4866}}+t\,{\tbinom {100}{88245}}

mit

t\in \mathbb {R}

2. Lineares Gleichungssystem aufstellen:

{\begin{matrix}I.&0&+&100t&=&x_{1}\\{\mathit {II}}.&-4866&+&88245t&=&18312\end{matrix}}

Daraus ergibt sich nach entsprechenden Äquivalenzumformungen folgendes LGS

{\begin{matrix}I.&100t&=&x_{1}\\{\mathit {II}}.&t&=&{\frac {23178}{88245}}\end{matrix}}

3. Setze $t={\frac {23178}{88245}}$ in $I.$ :

x_{1}=100*{\frac {23178}{88245}}\approx 26.27

Insgesamt folgt nun:

Unternehmen 1 benötigt staatliche Hilfen in Höhe von 26.27% (vgl. Abb. 8) des Umsatzes vor Corona, um auch während des Lockdowns den gleichen Gewinn zu erzielen als zuvor.

Abb. 8: Staatliche Zuschüsse Zyklus 2
	Unternehmen 1	Unternehmen 2	Unternehmen 3	Unternehmen 4	Unternehmen 5	Durchschnitt
Staatliche Zuschüsse (%)	26,27 %	18,82 %	44,87 %	37,56 %	25,11 %	29,73 %

Dieser Rechenweg kann analog für die vier weiteren Unternehmen durchgeführt werden und man erhält ebenfalls die gleichen staatlichen Zuschüsse wie zuvor mit den linearen Funktionen (vgl. Abb. 8). Damit gibt es, wie so oft in der Mathematik, mehrere Wege, die zur Problemlösung verhelfen können. Je weiter der mathematische Horizont erweitert ist, desto mehr Mittel stehen einem zur Verfügung, um die Probleme zu lösen.

Bewertung 2[Bearbeiten]

Wie auch in der Bewertung 1 haben wir die durchschnittliche Abweichung (betragsmäßige Abweichung vom Gewinn vor Corona zum Gewinn während des Lockdowns + staatliche Zuschüsse) berechnet. Diese beträgt 4.484€ und ist deutlich geringer als die Abweichung bei dem 1. Modellierungszyklus. Dementsprechend sind die Zuschüsse "gerechter" verteilt worden, da sich nun der Gewinn während des Lockdowns mit Hilfe der staatlichen Zuschüsse an den Gewinn vor Corona annähert.

Optimierung 2[Bearbeiten]

Um nun ein Optimum auf Seiten des Staates und auf Seiten der Unternehmen zu erreichen, gilt es nun die Perspektive der Unternehmen abzulegen und die Perspektive des Staates einzunehmen. Um eine weitere Optimierung zu erreichen, sollen im Folgenden einige zusätzliche Parameter berücksichtigt werden. Diese wären das Budget, welches dem Staat zur Verfügung steht und welches auf die fünf Unternehmen verteilt werden soll. Dies geschieht in Abhängigkeit sogenannter Gewichtungsfaktoren, welche den Unternehmen individuell zugeordnet werden. Des Weiteren soll auch die Veränderung der Mitarbeiterzahlen eine Rolle spielen. Ein Ziel der Optimierung soll es sein, so viele Arbeitsplätze wie möglich zu erhalten. Es gilt hier zu beachten, dass entlassene Arbeitnehmer ebenfalls auf staatliche Hilfsmittel angewiesen sind und die Kosten für den Staat erhöhen. Ein weiteres Optimierungsziel ist es, die Staatskosten bei möglichst wenigen Entlassungen auf dem Arbeitsmarkt so gering wie möglich zu halten.

Modellierungszyklus 3[Bearbeiten]

Aufstellen der Kostenfunktion[Bearbeiten]

Die Kostenfunktion k entsteht in Abhängigkeit des Budgets b, welches dem Staat zur Verfügung steht und des Gewinns g, welcher vom Staat durch Lohnsteuer-Einnahmen erwirtschaftet wird. Außerdem in Abhängigkeit der Arbeitslosigkeit a, welche den Staat zusätzlich belastet, da er Arbeitslosengeld zahlen muss. Das maximale Budget $b_{max}$ wurde von uns auf 100.000€ festgelegt. Der Gewinn setzt sich zusammen aus der Differenz des durchschnittlichen Bruttogehalts (2.800€) und des durchschnittlichen Nettogehalts (2120€) und ist des Weiteren abhängig von der Anzahl der geretteten Arbeitsplätze n. Die Differenz entspricht 680€ und wird mit n multipliziert. Die Arbeitslosigkeit entsteht in Abhängigkeit der geretteten Arbeitsplätze, welche mit dem Betrag von 1272€ multipliziert werden. Dieser Betrag setzt sich zusammen aus dem durchschnittlichen Nettogehalt aller Angestellten multipliziert mit dem Faktor 0,6, welcher den Anteil des Arbeitslosengeldes darstellt.

Die Kostenfunktion sieht daher wie folgt aus:

k(b,g,a):=b+a-(g+(b_{max}-b))

Die Funktionen $g(n)$ und $a(n)$ sind definiert als:

g(n):=680*n

a(n):=1272*(23-n)

Abb. 11: Aufstellen der Kostenfunktion

(%i1) k(b,g,a):=b+a-(g+(100000-b));
(%o1) k(b,g,a):=b+a-(g+(100000-b))

(%i2) k(b,680·n,1272·(23-n));
(%o2) -680n+1272(23-n)+2b-100000

(%i3) ratsimp(%o2);
(%o3) -1952n+2b-70744

(%i4) k(b,n):=(-1952)·n+2·b-70744;
(%o4) k(b,n):=(-1952)n+2b-70744

Setzt man $g(n)$ und $a(n)$ in die Kostenfunktion $k(b,g,a)$ ein, so erhält man nach Vereinfachung folgende endgültige Kostenfunktion:

k(b,n):=(-1952)*n+2*b-70744

mit

b\in [0,100.000]

und

n\in [0,23]

Verteilung des Budgets[Bearbeiten]

Die Wahrscheinlichkeitsverteilung des Budgets für die fünf Unternehmen wurde mit Hilfe der Fuzzy-Logik ermittelt. Dabei wurde jedem Unternehmen eine Gewichtung $g_{1},...,g_{5}\in [0,1]$ zugeordnet. Die Gewichtung eines einzelnen Unternehmens geteilt durch die Summe der Gewichtungen ergibt die Wahrscheinlichkeitsverteilungen $p_{1},...,p_{5}\in [0,1]$ $mit$ $p_{1}+...+p_{5}=1$ . Durch systematisches Probieren erhielten wir eine für unser Modell optimale Gewichtung. Diese sieht wie folgt aus:

g_{1}=0,6

g_{2}=0,2

g_{3}=0,1

g_{4}=0,6

g_{5}=0,3

g_{gesamt}=1,8

p_{1}={\frac {0,6}{1,8}}={\frac {1}{3}}

p_{2}={\frac {0,2}{1,8}}={\frac {1}{9}}

p_{3}={\frac {0,1}{1,8}}={\frac {1}{18}}

p_{4}={\frac {0,6}{1,8}}={\frac {1}{3}}

p_{5}={\frac {0,3}{1,8}}={\frac {1}{6}}

p_{gesamt}=1

Das maximale Budget $b_{max}$ wurde auf $100.000$ € festgelegt.

Minimales Budget der einzelnen Unternehmen[Bearbeiten]

Hierfür betrachtet werden der Gewinn während des Lockdowns und 20% des Gewinns vor Corona. Der minimale staatliche Zuschuss an die Unternehmen ist der Betrag der Differenz zwischen den beiden oben genannten Werten. Das minimale Budget dient als Untergrenze für die Unternehmen, sodass diese keine Verluste einfahren und solvent bleiben.

Gerettete Arbeitsplätze[Bearbeiten]

Zu verschiedenen Werten für $b$ wurden die geretteten Arbeitsplätze der einzelnen Unternehmen bestimmt. Anschließend wurden diese aufsummiert woraus die Gesamtzahl der geretteten Arbeitsplätze resultierte. Die geretteten Arbeitsplätze der einzelnen Unternehmen lassen sich wie folgt berechnen:

Benötigtes Budget & gerettete Arbeitsplätze

(%i5) b_1(n_1):=8500+n_1·2800;
(%o5) b₁(n₁):=8500+n₁·2800

(%i6) n_1(b_1):=(b_1-8500)/2800;
(%o6) n₁(b₁):=(b₁-8500)/2800

(%i7) b_2(n_2):=1000+n_2·2800;
(%o7) b₂(n₂):=1000+n₂·2800

(%i8) n_2(b_2):=(b_2-1000)/2800;
(%o8) n₂(b₂):=(b₂-1000)/2800

(%i9) b_3(n_3):=4400+n_3·0;
(%o9) b₃(n₃):=4400

(%i10) b_4(n_4):=27800+n_4·2800;
(%o10) b₄(n₄):=2800·n₄+27800

(%i11) n_4(b_4):=(b_4-27800)/2800;
(%o11) n₄(b₄):=(b₄-27800)/2800

(%i12) b_5(n_5):=2900+n_5·2800;
(%o12) b₅(n₅):=2800·n₅+2900

b_{1}(n_{1})=8.500+n_{1}*2800

n_{1}(b_{1})={\frac {b_{1}-8500}{2800}}

b_{2}(n_{2})=1.000+n_{2}*2800

n_{2}(b_{2})={\frac {b_{2}-1000}{2800}}

b_{3}=4.400

b_{4}(n_{4})=27800+n_{4}*2800

n_{4}(b_{4})={\frac {b_{4}-27800}{2800}}

b_{5}(n_{5})=2.900+n_{5}*2800

n_{5}(b_{5})={\frac {b_{5}-2900}{2800}}

Benötigtes Budget & gerettete Arbeitsplätze

(%i13) n_5(b_5):=(b_5-2900)/2800;
(%o13) n₅(b₅):=(b₅-2900)/2800

(%i14) n_gesamt(b_1,b_2,b_3,b_4,b_5):=((b_1-8500)/2800)+((b_2-1000)/2800)+((b_4-27800)/2800)+((b_5-2900)/2800);
(%o14) n_gesamt(b₁,b₂,b₃,b₄,b₅):=((b₁-8500)/2800)+((b₂-1000)/2800)+((b₄-27800)/2800)+((b₅-2900)/2800)

(%i15) ratsimp(%o14);
(%o15) n_gesamt(b₁,b₂,b₃,b₄,b₅):=(b₅+b₄+b₂+b₁-40200)/2800

(%i16) b_gesamt(n_1,n_2,n_3,n_4,n_5):=(8500+n_1·2800)+(1000+n_2·2800)+4400+(27800+n_4·2800)+(2900+n_5·2800);
(%o16) b_gesamt(n₁,n₂,n₃,n₄,n₅):=2800n₅+2800n₄+2800n₂+2800n₁+44600

n_{gesamt}(b_{1},b_{2},b_{4},b_{5})=({\frac {b_{1}-8500}{2800}})+({\frac {b_{2}-1000}{2800}})+({\frac {b_{4}-27800}{2800}})+({\frac {b_{5}-2900}{2800}})

b_{gesamt}(n_{1},n_{2},n_{4},n_{5})=(8.500+n_{1}*2800)+(1.000+n_{2}*2800)+4.400+(27800+n_{4}*2800)+(2.900+n_{5}*2800)

Intervallschachtelung[Bearbeiten]

Zuerst wurde das Startintervall $[0,100.000]$ für $b$ betrachtet. Durch das Intervallhalbierungsverfahren erhielten wir verfeinerte Intervalle für $b$ . Dabei wurde jedem b-Wert ein n-Wert zugeordnet. Mit Hilfe dieser Schachtelung wurde die maximale Anzahl an geretteten Arbeitsplätzen zu einem möglichst geringen Budget ausfindig gemacht. Mit einem maximalen Budget von 100.000€ können maximal 15 von 23 Arbeitsplätze gerettet werden. Diese 15 Arbeitsplätze können schon ab ca. 92.700,20€ gerettet werden.

Intervallschachtelung
Budget	n(ges. AP)	Kosten	Budget/AP
0,00 €	0	-70.744,00 €
100.000,00 €	15	99.976,00 €	6.666,67 €
75.000,00 €	10	59.736,00 €	7.500,00 €
87.500,00 €	13	78.880,00 €	6.730,77 €
93.750,00 €	15	87.476,00 €	6.250,00 €
90.625,00 €	13	85.130,00 €	6.971,15 €
92.187,50 €	14	86.303,00 €	6.584,82 €
92.968,75 €	15	85.913,50 €	6.197,92 €
92.578,13 €	14	87.084,25 €	6.612,72 €
92.773,44 €	15	85.522,88 €	6.184,90 €
92.675,78 €	14	87.279,56 €	6.619,70 €
92.724,61 €	15	85.425,22 €	6.181,64 €
92.700,20 €	15	85.376,39 €	6.180,01 €
92.687,99 €	14	87.303,98 €	6.620,57 €
92.694,09 €	14	87.316,18 €	6.621,01 €
92.697,14 €	14	87.322,29 €	6.621,22 €
92.698,67 €	14	87.325,34 €	6.621,33 €
92.699,43 €	14	87.326,86 €	6.621,39 €
92.699,81 €	14	87.327,63 €	6.621,42 €
92.700,00 €	14	87.328,01 €	6.621,43 €

Bewertung 3[Bearbeiten]

Für das maximale Budget von 100.000 € ergab sich, dass schon ab ca. 92.700€ die maximale Anzahl an Arbeitsplätze (n= 15) gerettet werden können. Dabei betragen die Kosten ca. 85.376€. Im Vergleich dazu, fallen bei einem Budget von 100.000€ ca. 99.976€ Kosten an. Diese sind höher als bei 92.700€, da nicht mehr als 15 Arbeitsplätze gerettet werden konnten. Damit wurde unser Modellierungsziel, die maximal geretteten Arbeitsplätze für das entsprechende minimale Budget zu bestimmen, erreicht.

Optimierung 3[Bearbeiten]

Mit dem von uns gewählten maximalen Budget von 100.000€ konnten nicht alle Arbeitsplätze (n=23) gerettet werden. Somit müsste der Staat das Budget maximieren, um alle Arbeitsplätze zu retten. Aufgrund dessen das die finanziellen Ressourcen des Staates begrenzt sind, ist es nicht möglich dem nachzukommen. Des Weiteren stellt sich die Frage, ob es sinnvoll ist in ein Unternehmen zu investieren bei denen keine Arbeitsplätze gesichert werden können. Um diese Frage zu beantworten, müssten weitere Parameter (Bsp.: Gewerbesteuer der einzelnen Unternehmen, Kaufkraft) betrachtet werden.

Teilprojekt 3[Bearbeiten]

Theorie[Bearbeiten]

Vergleich der Maßnahmen unter den Ländern[Bearbeiten]

Schweden[Bearbeiten]

Der erster bestätigte Fall einer Covid-19 Infektion wurde am 31.Januar 2020 registriert. Seitdem geht Schweden einen "Sonderweg", der sich durch wenig bis keine gesetzlichen Maßnahmen kennzeichnet. Die Regierung sprach Empfehlungen aus und appelierte an die Vernunft der Bürger. Die Empfehlungen lauteten:

Zuhause bleiben, falls man sich krank fühlt
häufiges Händewaschen
Kontakte reduzieren
nicht zwingend nötige Inlandsreisen vermeiden

Im Laufe des Jahres gab es einige wenige verbindliche Vorschriften. Bis Juni 2020 galt Fernunterricht ab der 10. Klassenstufe und an Universitäten. Im Zeitraum vom 1. April bis zum 1. Oktober galt ein Besucherverbot von Altersheimen und Pflegeeinrichtungen. Der Verzehr von Speisen und Getränken war in Bars nur sitzend am Tisch erlaubt und der Thekenaufenthalt war somit verboten. Ab dem 29.März galt ein Veranstaltungsverbot für Gruppen über 50 Personen. Am 24. November wurde die Zulässigkeit für Personenansammlungen in der Öffentlichkeit auf eine Maximalzahl von 8 Personen festgelegt.^[8]

Südkorea[Bearbeiten]

Der erste bestätigte Fall einer Covid-19 Infektion trat in Südkorea am 20. Januar 2020 auf. Ab dem 19.02. 2020 konnte ein rapider Anstieg der Fallzahlen beobachtet werden, wofür ein Superspreader-Event in der Shincheonji-Gemeinschaft verantwortlich war.

Zahlen:

Einwohnerzahl 51,63 Millionen
Infizierte 34043 (Infektionsrate 0,06%)
24.735 Genesene (Genesungsrate 81,4%)
Verstorbene 476 (Mortalitätsrate 1,6%)
Stand 21.11.2020

Maßnahmen:

Durchführung von Tests
Identifikation von Clustern und von Kontaktpersonen
Grenzkontrollen
Isolation
Sozial Distancing

(Daten: KCDC - Korea Centers for Disease Control and Prevention)

Italien[Bearbeiten]

Bereits im November 2019 wurde der erste Fall in Italien bestätigt. Somit ist Italien eines der Länder in Europa die relativ schnell und auch sehr stark betroffen war. Die höchsten Fallzahlen aber waren in Norditalien vorhanden, sodass sogar das Gesundheitssystem überlastet war. Anfang November teilte man in drei Gefahrenstufen ein:

Höchste Gefahrenstufe (rot):

Ganztägige Ausgangssperren
Verbot in andere Städte zu fahren
Bars und Restaurants geschlossen
Präsenzunterricht für Schüler bis zur sechsten Klasse, sonst Fernunterricht

Mittlere Gefahrenstufe (orange)

Ausgangssperre von 22 Uhr bis 5 Uhr morgens
Bars und Restaurants geschlossen
Präsenzunterricht bis zur neunten Klasse, sonst Fernunterricht

Niedrigste Gefahrenstufe (gelb):

Präsenzunterricht bis zur neunten Klasse, sonst Fernunterricht

Deutschland[Bearbeiten]

Der erste bestätigte Fall der Erkrankung wurde am 27. Januar 2020 bestätigt. Die Gefahr für die Bevölkerung wurde zunächst am 28. Februar als "gering bis mäßig" bewertet, seit dem 17. März 2020 als "hoch" und für Risikogruppen sogar als "sehr hoch" eingestuft. Am 13. und 17. März wurden einige Maßnahmen zur Bekämpfung der Pandemie getroffen:

Kontaktbeschränkungen
14- tägige häusliche Quarantänepflicht für Rückkehrer aus dem Ausland
Schließung zahlreicher Geschäfte auch Restaurants und Bars, Dienstleistungsbetriebe
Maskenpflicht im öffentlichen Nahverkehr und in Geschäften
Absage von Veranstaltungen mir >1000 Teilnehmern
keine Großveranstaltungen bis 31. August
vorsichtige und gezielte Öffnung von Bildungseinrichtungen und öffentlichen Leben

Anfang Mai wurden einige dieser Maßnahmen Schritt für Schritt aufgehoben, jedoch stiegen die Infektionszahlen rasant an so, dass im Herbst 2020 die Maßnahmen wieder verschärft werden müssen. Ab November 2020 wurden weitgehend Einschränkungen sozialer Kontakte getroffen.

Modellierungszyklus 1[Bearbeiten]

Mithilfe eines Tabellenkalkulationsprogramms, Libre Office Calc, haben wir zu den vier verschiedenen Ländern Tabellen^[9] zu dem SIR-Modell erstellt mit den Spalten:

t(Zeit)
S(Personen, die sich potenziell mit dem Virus anstecken können)
I(aktuell Infizierte)
R (Recovered, genesene Personen)
BRZ (Basisreproduktionszahl, die Anzahl an Personen, die eine infizierte Person im Durchschnitt ansteckt)
nächstes I (Anzahl infizierte Personen nach einem Zeitschritt)
Einwohnerzahl
Zeitschritte in Tagen

Zuerst haben wir die realen Fallzahlen und Verläufe in dem jeweiligen Land recherchiert und diese dann in die Tabelle übertragen. Als nächstes haben wir die Basisreproduktionszahl so angepasst, dass die modellierte Kurve mit den realen Daten gleichen. Das Modell zeigt, wie die Verläufe des jeweiligen Landes sich verändern in Bezug auf die Basisreproduktionszahl. Wenn die Basisreproduktionszahl gering ist, sieht man, dass Maßnahmen ergriffen wurden wie zum Beispiel Kontaktbeschränkungen.

Bewertung 1[Bearbeiten]

Die Werte wurden so lange angepasst, bis die modellierten Kurven der realen Kurven gleichen. Dabei wird modelliert, wie sich die Verläufe der Kurve verändern, wenn sich die Basisreproduktionszahl ab einem bestimmten Zeitpunkt erhöht bzw. verringert.

Optimierung 1[Bearbeiten]

SIR-Modell Schweden 2019 mit logarithmierter y-Achse (eigene Erstellung)

Modellierungszyklus 2[Bearbeiten]

Um die Verteilung des Corona-Virus zwischen den ausgewählten Ländern besser zu veranschaulichen, haben wir ein Modell mit Hilfe von Matrizenrechnungen erstellt. Da der Virus über mehrere Wege in die verschiedenen Ländern gelangen kann, haben wir uns auf die Flugpassagierzahl konzentriert, da die gewählten Länder meist über den Flugverkehr bereist werden.

Bewertung 2[Bearbeiten]

Im Modell wird eine 4x4 Matrix mit einem 4x1 Vektor multipliziert. Um es besser darzustellen, wird hier eine 2x2 Matrix mit einer 2x1 Matrix multipliziert.

${}{\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ $\cdot \left({\begin{array}{c}x\\y\end{array}}\right)$

Um zwei Matrizen miteinander multiplizieren zu können, muss die Spaltenzahl der ersten Matrix mit der Zeilenzahl der zweiten Matrix übereinstimmen. In dem Fall besitzt die Spalte der 2x2 Matrix genau zwei Werte und die Zeile des 2x1 Vektors ebenso. Somit können die Matrix und der Vektor miteinander multipliziert werden und man erhält eine Matrix der Form C = A * B also eine 2x1 Matrix. Zur Berechnung des ersten Elements cij der Produktmatrix wird die i-te Zeile der ersten Matrix (in diesem Fall a und b) mit der j-ten Spalte der zweiten Matrix (in diesem Fall x und y) "multipliziert" und zwar im Sinne eines Skalarprodukts:

${}{\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ $\cdot \left({\begin{array}{c}x\\y\end{array}}\right)=\left({\begin{array}{c}ax+by\\cx+dy\end{array}}\right)$

Optimierung 2[Bearbeiten]

Um die Verteilungsprozesse zwischen Ländern zu ermitteln, wird eine Transportmatrix A aufgestellt. In der Matrix A stehen dann die Zu- und Abgänge der jeweiligen Länder. Die Transportmatrix A wird dann mit einem Vektor x multipliziert in denen dann die jeweiligen Einwohnerzahlen der Länder aufgelistet sind. Matrizen können nur multipliziert werden, wenn die Spaltenanzahl der Matrix A der Zeilenanzahl der Matrix B entspricht (A= mxl und B= lxn). In einer beliebigen Spalte (z.B. "k") stehen dann in den jeweiligen Zeilen der Abgang, der prozentual zur Einwohnerzahl des k-ten Landes angegeben wird. Bei der Multiplikation. Daher ist die Spaltensumme stets 1. Die Matrixmultiplikation $A\cdot x$ ergibt dann den neuen Vektor $x'$ . $x'$ beschreibt dann die Einwohnerzahl der Länder nach dem Transportprozess.

Beispielhaft wird nun im ersten Schritt die Verteilung der Einwohner anhand einer 2x2 Matrix A und einem 2x1 Vektor x erklärt. Man erstellt eine Matrix mit den Einträgen $a_{ii},\;a_{ij},\;a_{ji}$ und $a_{jj}$ . Der Eintrag $a_{ii}$ stellt den prozentualen Anteil derer dar, die in Land i geblieben sind (nicht geflogen), der Eintrag $a_{ij}$ stellt den Anteil derer dar, die von i nach j geflogen sind. Der Vektor x beschreibt die Einwohnerzahl der untersuchten Länder, der Vektor x' beschreibt die Einwohnerzahl der untersuchten Länder nach dem Transportprozess.

${}{\begin{pmatrix}a_{ii}&a_{ji}\\a_{ij}&a_{jj}\end{pmatrix}}$ $\cdot \left({\begin{array}{c}x_{i}\\x_{j}\end{array}}\right)=\left({\begin{array}{c}x'_{i}\\x'_{j}\end{array}}\right)$

Um eine Abschätzung zu treffen, wie viele Flugpassagiere von einem Land zum anderen Land fliegen, werden einige Annahmen getroffen:

Migration ist vernachlässigbar, zwischen zwei Ländern gilt also: $a_{ij}=a_{ji}$
Innerhalb eines Landes findet ebenfalls Flugverkehr statt (gilt nur für Länder mit mehreren Flughäfen)
Die Anzahl der Flüge von Land I in ein Land J soll gewichtet nach der Gesamtanzahl der Flugpassagiere von I und J sein: $a_{ij}={\frac {n_{i}n_{j}}{n}}$ mit $n$ : Passagieraufkommen pro Tag weltweit und $n_{k}$ : Passagieraufkommen pro Tag des Landes K
Die Anzahl der Flüge ist unabhängig von der Entfernung der Länder und der Zeit

Gedankenexperiment: Nehmen wir an, in Südkorea bricht eine Krankheit aus, die sich durch Viren übertragen lässt. Die Basisreproduktionszahl wird auf 1,17 geschätzt und das Land Schweden möchte nun wissen, wie das Infektionsgeschehen bei ihnen abläuft, wenn der Flugverkehr (einzige Möglichkeit zur Einschleppung des Virus) normal weiter läuft. Unter Einbindung des Transportprozesses bestimmt sich die Suszeptibilität $S'$ des Tages $t$ durch:

$\left({\begin{array}{cc}1-{\frac {n_{i}n_{j}}{nS_{i}}}{\frac {S_{i}}{N_{i}}}&{\frac {n_{i}n_{j}}{nS_{j}}}{\frac {S_{j}}{N_{j}}}\\{\frac {n_{i}n_{j}}{nS_{i}}}{\frac {S_{i}}{N_{i}}}&1-{\frac {n_{i}n_{j}}{nS_{j}}}{\frac {S_{j}}{N_{j}}}\end{array}}\right)_{t}\left({\begin{array}{c}S_{i}\\S_{j}\end{array}}\right)_{t}=\left({\begin{array}{c}S'_{i}\\S'_{j}\end{array}}\right)_{t}$

$I$ und $R$ lassen sich analog bestimmen. Man bedenke, dass $(S_{k})_{t}=N-(I_{k})_{t}-(R_{k})_{t}$ ist.

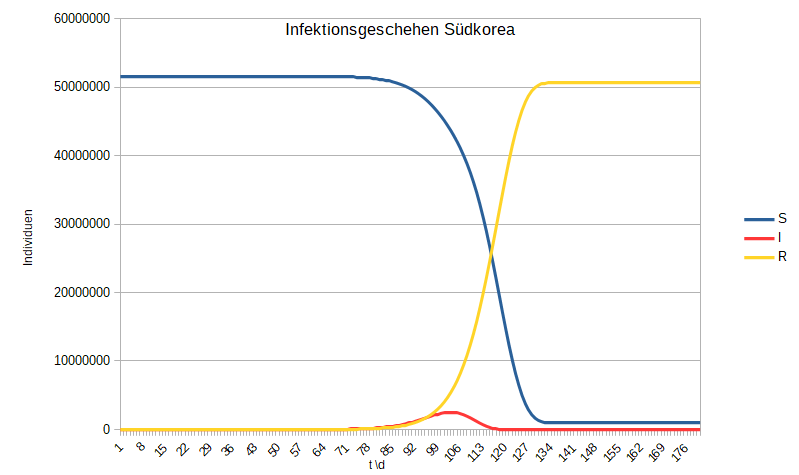
Die Grafiken beschreiben das Infektionsgeschehen in Schweden und Südkorea. Sie beginnen zeitgleich mit einer infizierten Person in Südkorea. An Tag 46 $(\pm 3\;d)$ befindet sich vermutlich auch in Schweden erstmals eine infizierte Person. Die Zahl der Infizierten in Südkorea hat am Tag 103 ihr Maximum (Tag 134 in Schweden). Durch den Transportprozess entwickelt sich das Infektionsgeschehen in Schweden schneller als in Südkorea (der Virus benötigt ca. 15 Tage weniger um sein Maximum zu erreichen).

Modellierungszyklus 3[Bearbeiten]

Einschub Bernoullische Differentialgleichung^[10]

Eine DGL der Gestalt $f'(t)=kGf(t)-kf^{2}(t)$ ^[11] lässt sich wie folgt lösen:

Transformiere $g(x)=f(t)^{-1}$ , dann $g(t)={\frac {1}{f(t)}}\Rightarrow g'(t)=-{\frac {f'(t)}{f^{2}(t)}}$ .

Damit ergibt sich die lineare DGL $g'(t)=-(kGf(t)^{-1}-k)=-kGg(t)+k$

Lösen der homogenen DGL $g_{h}'(t)+kGg_{h}(t)=0$ ergibt $g_{h}(t)=g_{0}e^{-kGt+\delta }$ mit $\delta =kGc$
Die partikulare Lösung ist $g_{p}(t)={\frac {k}{kG}}-{\frac {1}{G}}e^{-kGt+\delta }$ und mit $g(0)=g_{0}={\frac {1}{f_{0}}}={\frac {1}{f(0)}}$ ergibt sich:

$g(t)={\frac {1}{G}}+\left({\frac {1}{f_{0}}}-{\frac {1}{G}}\right)e^{-kGt+\delta }$ .
Da $f(t)={\frac {1}{g(t)}}\Rightarrow f(t)={\frac {G}{1+({\frac {G}{fo}}-1)e^{-kGt+\delta }}}$ mit $\delta =kGc$
Durch Ersetzungen $f(t)\;{\overset {allg.}{=}}\;\left({\frac {4A}{\alpha \left(1+e^{-\alpha (t-c)}\right)}}\right)$

Betrachten wir die beidseitige Ableitung der Bernoullische Differentialgleichung, so stellt $f'(t)=\left({\frac {4Ae^{-\alpha (t-c)}}{\left(1+e^{-\alpha (t-c)}\right)^{2}}}\right)$ eine Lösung der DGL $f''(t)=kGf'(t)-2kf(t)f'(t)$ dar.

SIR-Modell Für das SIR-Modell werden drei DGL verwendet ( $N=const.$ ):

$S'=-\alpha {\frac {SI}{N}}$
$I'=\alpha {\frac {SI}{N}}-\beta I$

$R'=\beta I$

Es gilt $N=S+I+R=const.$

Die DGL für die Infiziertenzahl lässt sich also wie folgt schreiben: $I'=\alpha {\frac {(N-R-I)}{N}}I-\beta I=\left(\left(1-{\frac {R}{N}}\right)\alpha -\beta \right)I-{\frac {\alpha }{N}}I^{2}=\left(\left(1-{\frac {\beta }{N}}\int Idt\right)\alpha -\beta \right)I-{\frac {\alpha }{N}}I^{2}$

Ist der letzte Term $(-{\frac {\alpha }{N}}I^{2})$ vernachlässigbar, so erhalten wir die DGL:

$I'=(\alpha -\beta )I-{\frac {\alpha \beta }{N}}\int Idt\cdot I$ und setzen $I(t)=f'(t)$ ; mit $f'(t)$ aus der Ableitung der Bernoullische Differentialgleichung, dann kennen wir bereits die Lösung:

$\left(I(t)=\left({\frac {4a\cdot k\cdot e^{-k(t-c)}}{\left(1+e^{-k(t-c)}\right)^{2}}}\right)\right)$

Um die Maßnahmen gegen Covid-19 (externe Größen einmal außen vor gelassen) miteinander vergleichen zu können, wird anhand der realen Daten der Länder eine nichtlineare Regression mit der Methode der kleinsten Quadratur^[12] durchgeführt. $min{\underset {i=n}{\overset {n}{\sum }}}(y_{i}-f(x_{i}))^{2}$ .
Um das Minimum der Summe der quadrierten Residuen zu finden gilt $\left(2{\underset {n}{\sum }}(y_{i}-f(x_{i}))\right)f'(x_{i}){\overset {!}{\approx }}0$
R gibt dann ein Schätzintervall für die Werte von $a,\;c$ und $k$ raus in denen die Werte zu $95\;\%$ liegen. Für eine Bewertung der Maßnahmen sagt ${\frac {a\cdot k}{N}}$ etwas über die Schwere der Epidemie, $k$ etwas über die Ausbreitungsgeschwindigkeit und $c$ etwas über die Dauer zum vorläufigen Höhepunkt der Epidemie aus.

Ergänzung:

Allgemein ist $(-{\frac {\alpha }{N}}I^{2})$ nicht vernachlässigbar. Weil $I'(t)\sim (-{\frac {\alpha }{N}}I^{2})$ und daher die Ableitung für größere $I$ sinkt, bietet es sich an für die Kurvenanpassung die Ableitung einer asymmetrischen Sigmoidfunktion (wie z.B. der Gompertz-Funktion) zu verwenden:

$I(t)=a\cdot b\cdot e^{\left(-e^{(-b\cdot (t-c)}-b\cdot (t-c)\right)}$

Die Bewertung der Maßnahmen über die Parameter erfolgt analog zur vorherigen Funktion. Man muss hier nur $b$ durch $k$ ersetzen.

Bewertung 3[Bearbeiten]

Land	${\frac {k\cdot a}{N}}\cdot 10^{-4}$	$c$	$k$
Deutschland	0,71	41,05	0,15
Italien	0,88	35,15	0,1
Schweden	0,64	52,65	0,09
Südkorea	0,12	43,25	0,29

Optimierung 3[Bearbeiten]

Die Auswertung der Parameter für die Ableitung der Gompertzfunktion nach der Methode der kleinsten Quadrate ergibt:

Land	${\frac {a\cdot b\cdot e^{-1}}{N}}\cdot 10^{-4}$	$b$	$c$
Deutschland	0,68	0,09	39,15
Italien	0,89	0,07	35,5
Schweden	0,64	0,04	56,6
Südkorea	0,12	0,2	42,05

[Geogebra: Parametereinstellungen der Fitfunktion]

Modellierungsalternativen[Bearbeiten]

Teilprojekt 1[Bearbeiten]

Wie in der Diskussion bereits erwähnt hätte man den von Fenster 1 zu Fenster 4 abnehmenden Volumenstrom durch Korrekturfaktoren direkt in die Funktionsgleichung einbetten können. Außerdem hätte man statt dem Computer Algebra System Maxima das System Octave nutzen können. Die Lüftungsgütefunktion war zu kompliziert für Maxima und da Maxima und das Programm ist an seine Grenzen gekommen. Da Octave eher numerisch löst, hätte dieses Programm eine Chance sein können, nicht die Näherungsfunktion f, sondern die tatsächliche Lüftungsgütefunktion n zu verwenden.

Teilprojekt 2[Bearbeiten]

Es hätte die Modellierungsalternativen gegeben, wären gewesen, die allerding

Verwendete Software für die Modellbildung[Bearbeiten]

Geben Sie hier die in Ihrem Projekt verwendet Software an und begründen, warum Sie diese für die Modellbildung eine geeignetes Werkzeug ist.

Teilprojekt 1[Bearbeiten]

GeoGebra

Mit GeoGebra lassen sich geometrische Zusammenhänge einfach und übersichtlich visuell Darstellen. Vor allem durch den Zugmodus wird die Darstellung dynamisch und ist deswegen passend für die Fragestellungen der Modellierung. Durch die Möglichkeit der dreidimensionale Darstellung des Klassenraums und der Lüftungsstrecken und den beliebig verschiebbaren Raumpunkt liefert GeoGebra optimale Bedingungen für die Visualisierung der Modellierung.

Maxima CAS

Mit dem Computer Algebra System Maxima wurde die Lüftungsgütefunktion erstellt und eine Fallunterscheidung wurde durch eine if-Bedingung umgesetzt. Ein 3d-Plot der Funktion wurde angefertigt und das Gradientenaufstiegsverfahren konnte implementiert werden.

Teilprojekt 2[Bearbeiten]

Tabellenkalkulation

Mithilfe der Tabellenkalkulation konnten Wertetabelle zu unseren Unternehmen erstellt werden. Dadurch erhielten wir eine Übersicht über die Einnahmen und Ausgaben der jeweiligen Unternehmen. Des Weiteren konnten Berechnungen z.B. für den Gewinn/ Kostendeckungsgrad und für das arithmetische Mittel bezüglich der Einnahmen vor Corona durchgeführt werden. Auch Diagramme konnten mit Hilfe von Tabellenkalkulation erstellt werden. Der Kostendeckungsgrad der einzelnen Unternehmen zu unterschiedlichen Zeiten (vor Corona, während 1.Lockdown, während Corona) konnte durch ein Säulendiagramm anschaulich visualisiert werden und ermöglichte einen besseren Überblick über die Gesamtsituation.

Im 3.Modellierungszyklus konnten die Verteilung des Budgets ermittelt und die Anzahl der gerettete Arbeitsplätze mit dem Tabellenkalkulationsprogramm berechnet werden. Das entsprechende Makro wurde für die Intervallschachtelung eingesetzt.

GeoGebra

Mit Hilfe von GeoGebra konnten Funktionen konstruiert werden. Außerdem konnten die Funktionen miteinander in Beziehung gesetzt, Schnittpunkte berechnet und Schieberegler erstellt werden.

Maxima CAS

Mit Maxima haben wir die Kostenfunktion aufgestellt und vereinfacht. Für einzelne Werte konnte die Kostenfunktion berechnet werden. Zur Visualisierung diente der 3D Plot. Durch die „for Schleife“ konnten einzelne Werte für eine Variable eingesetzt werden.

Teilprojekt 3[Bearbeiten]

Siehe auch[Bearbeiten]

COVID-19/Mathematische Modellbildung

Quellen/Literatur[Bearbeiten]

↑ Kurs:Mathematische Modellbildung/Themen/Corona-Modellierung. (23. November 2020). Wikiversity, . Abgerufen am 23. November 2020, 09:56 von https://de.wikiversity.org/w/index.php?title=Kurs:Mathematische_Modellbildung/Themen/Corona-Modellierung&oldid=667051.
↑ UN-Guidelines for Use of SDG logo and the 17 SDG icons (2019/05/10) - https://www.un.org/sustainabledevelopment/news/communications-material/
↑ Ceriello, A., Standl, E., Catrinoiu, D., Itzhak, B., Lalic, N. M., Rahelic, D., ... & Valensi, P. (2020). Issues of Cardiovascular Risk Management in People With Diabetes in the COVID-19 Era. Diabetes Care.
↑ Axel Wuttke (2013) - Universität Göttingen, Material für die Klassenstufen 7 und 8 - URL: http://unterrichtsmaterialien-chemie.uni-goettingen.de/material/7-8/V7-131.pdf - letzter Zugriff: 2020/11/16
↑ „Arithmetisches Mittel“. In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 13. Januar 2021, 17:11 UTC. URL: https://de.wikipedia.org/w/index.php?title=Arithmetisches_Mittel&oldid=207608959 (Abgerufen: 18. Januar 2021, 14:37 UTC)
↑ „Vektor“. In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 14. Januar 2021, 00:44 UTC. URL: https://de.wikipedia.org/w/index.php?title=Vektor&oldid=207621099 (Abgerufen: 2. Februar 2021, 18:34 UTC)
↑ "Parameterform" In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 6. November 2019, 18:38 UTC. URL: https://de.wikipedia.org/w/index.php?title=Parameterform&oldid=193818222 (Abgerufen: 4. Februar 2021, 10:11 UTC)
↑ https://www.zdf.de/nachrichten/politik/corona-schweden-sonderweg-100.html
↑ https://niebert.github.io/wikiversity_files/index.html
↑ https://de.wikipedia.org/wiki/Bernoullische_Differentialgleichung
↑ https://de.wikipedia.org/wiki/Logistische_Funktion
↑ https://mathepedia.de/Methode_der_kleinsten_Quadrate.html

[1] Kurs:Mathematische Modellbildung/Themen/Corona-Modellierung. (23. November 2020). Wikiversity, . Abgerufen am 23. November 2020, 09:56 von https://de.wikiversity.org/w/index.php?title=Kurs:Mathematische_Modellbildung/Themen/Corona-Modellierung&oldid=667051.

[2] UN-Guidelines for Use of SDG logo and the 17 SDG icons (2019/05/10) - https://www.un.org/sustainabledevelopment/news/communications-material/

[3] Ceriello, A., Standl, E., Catrinoiu, D., Itzhak, B., Lalic, N. M., Rahelic, D., ... & Valensi, P. (2020). Issues of Cardiovascular Risk Management in People With Diabetes in the COVID-19 Era. Diabetes Care.

[4] Axel Wuttke (2013) - Universität Göttingen, Material für die Klassenstufen 7 und 8 - URL: http://unterrichtsmaterialien-chemie.uni-goettingen.de/material/7-8/V7-131.pdf - letzter Zugriff: 2020/11/16

[5] „Arithmetisches Mittel“. In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 13. Januar 2021, 17:11 UTC. URL: https://de.wikipedia.org/w/index.php?title=Arithmetisches_Mittel&oldid=207608959 (Abgerufen: 18. Januar 2021, 14:37 UTC)

[6] „Vektor“. In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 14. Januar 2021, 00:44 UTC. URL: https://de.wikipedia.org/w/index.php?title=Vektor&oldid=207621099 (Abgerufen: 2. Februar 2021, 18:34 UTC)

[7] "Parameterform" In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 6. November 2019, 18:38 UTC. URL: https://de.wikipedia.org/w/index.php?title=Parameterform&oldid=193818222 (Abgerufen: 4. Februar 2021, 10:11 UTC)

[8] ttps://www.zdf.de/nachrichten/politik/corona-schweden-sonderweg-100.html

[9] ttps://niebert.github.io/wikiversity_files/index.html

[10] ttps://de.wikipedia.org/wiki/Bernoullische_Differentialgleichung

[11] ttps://de.wikipedia.org/wiki/Logistische_Funktion

[12] ttps://mathepedia.de/Methode_der_kleinsten_Quadrate.html

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]