Kurs:Mathematische Modellbildung/Themen/Corona-Modellierung/Zyklus 1 Teilprojekt 1

Einführung in das Thema

Kurzvorstellung

Untersuchen der Luftqualität in Klassenräumen im Hinblick auf die Sitzordnung

• im ersten Lockdown (März 2020) Schließungen von jeglichen Bildungseinrichtungen

• Präsenzunterricht soll nicht mehr ausfallen

• deshalb mittlerweile (seit Juni 2020) Hygiene-Konzepte, die neben den AHA-Regeln auch regelmäßiges Lüften vorsehen

• aufgrund dieser Relevanz Thema dieses Projekts

Mathematische Aspekte

Fragestellung der Modellierung:

Wie gut werden verschiedenen Raumpunkte und Bereiche in einem Klassenzimmer gelüftet und was bedeutet dies für die Sitzordnung?

Bezug zur Mathematik

Modellierung auf verschiedenen Niveaus:

• Sekundarstufe 1: elementare Geometrie
• Sekundarstufe 2: analytische Geometrie
• Universität: mehrdimensionale Analysis
• verwendete Programme: Geogebra, Maxima

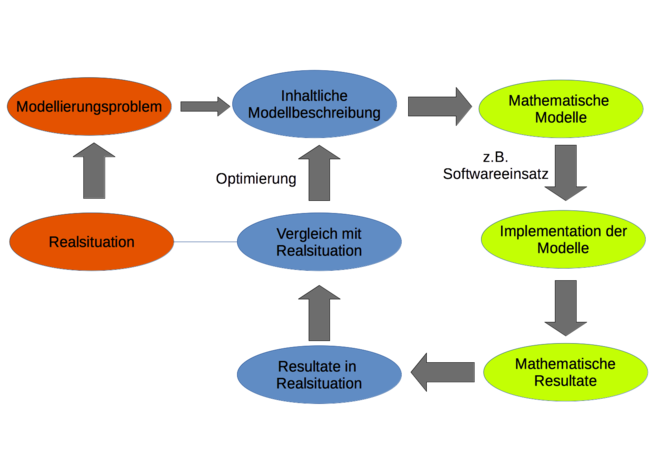
Ablauf eines Modellierungszyklus

Modell 1

• Beurteilung der Lüftungseffektivität durch Berechnung des Abstandes zu stark belüfteten Bereichen
• Je kleiner der Abstand zu stark belüfteten Bereichen, desto besser die Lüftungsqualität

Modellannahmen

• Darstellung des Raums als 2-Dimensionales Rechteck (Vogelperspektive)
• Stark belüftete Bereiche sind Strecken zwischen Fenster und Tür, die alle gleich stark und gut belüftet werden

Vogelperspektive Klassenzimmer

https://www.geogebra.org/m/uqp42wsr

Berechnungen

Konstruktion Hilfsdreiecke von zu beurteilendem Raumpunkt $P$ zu den Wänden.

Berechnungen

Die Strecken $a$ und $b$ sind im Koordinatensystem ablesbar. Die Strecke $c$ lässt sich mithilfe des Satz des Pythagoras berechnen.

$c={\sqrt {a^{2}+b^{2}}}$

Berechnungen

Analog werden weitere Hilfsdreiecke konstruiert um $d$ und $e$ zu berechnen

Berechnungen

Der Winkel $\angle P,T{\ddot {u}}r,Fenster=\alpha$ wird mithilfe des Kosinussatz berechnet.

$\alpha =\arccos({{e^{2}+d^{2}-c^{2}} \over {2ed}})$

Berechnungen

Der Abstand $s$ von Punkt $P$ zu der Strecke $e$ ist durch die Länge der Senkrechten von $e$ auf $P$ gegeben. Diese Länge kann mithilfe des Sinus berechnet werden.

$s=d\cdot sin{\alpha }$

[1]

Berechnungen

Falls der nächstgelegene Punkt auf der Lüftungsstrecke der Endpunkt der Strecke am Fenster ist, berechnet sich der Abstand einfach über den Satz des Pythagoras. Er ist die Länge der Hypothenuse des rechtwinkligen Hilfsdreiecks.

Modell 2

Fragestellung: Welcher Bereich des Raumes erfährt den größten Luftmassenaustausch?

Modellbildung

Vereinfachung/Annahmen:

• zweidimensionales Modell

• Im Bereich von Fenster 1 zur Tür herrscht der größte Volumenstrom, im Bereich zwischen Fenster 4 und Tür der kleinste.

• Überschneidungen der Flächen fließen additiv in das Modell ein.

• Kleine Bereiche neben den Fenstern erfahren einen Volumenstrom, allerdings kleiner als im direkten Lüftungsbereich.

Validierung

• Modell kann im Unterricht geprüft werden (Windmessgeräte)

• Übersicht über stark/schwach belüftete Raumpunkte in Abhängigkeit der Farbe

• In diesem Modell keinen Luftaustausch in der unteren rechten Ecke oder zwischen den Fenstern

Bewertung

Ziel: Lüftungsqualität innerhalb eines Klassenzimmers untersuchen und Folgen für Sitzordnung ableiten

Modell 1

Luftqualität zu allen Punkten der Ebene bestimmen

⇒ allgemeines Ziel erreicht

Probleme/Modellgrenzen:

• kein guter Überblick über die Luftqualität im gesamten Raum
• Lüftungsbereiche nur Linien ⇒ Vereinfachung ohne Aussagekraft zu verringern

Modell 2

Ziel: Schwächen des 1. Modells auszugleichen

• Luftströme als Flächen eingezeichnet mit unterschiedlich starker Lüftungsintensität -> bietet einen guten Überblick über die Luftqualität im gesamten Raum

Fazit (1)

• Beide Modelle tragen Ergebnis zur Fragestellung bei
• 1. Modell: Schwerpunkt, einzelne Raumpunkte zu betrachten
• 2. Modell: Schwerpunkt, einen Gesamteindruck über die Luftqualität im gesamten Klassenzimmer zu erhalten

Fazit (2)

• relativ kleiner gut belüfteter Bereich

⇒ kleinere Klassen oder Wechselunterricht

⇒ SuS mit Sicherheitsabstand in belüfteten Bereich

⇒ Lehrkraft in rechten Teil des Raumes mit ausreichend Abstand zu SuS

Optimierung

• Klassenraum zweidimensional ⇒ dreidimensionale Modellierung: Aussage ob Luftstrom in den Bereichen größer ist, welche den Aerosol-Ausstoß betreffen
• Annahme, dass zwischen einem Fenster und der Tür der Volumenstrom gleichbleibt
• Modell 2: viele unbelüftete (im Modell weiße) Bereiche ⇒ nicht komplett unbelüftet
• weiße Bereiche in Fensternähe stärker belüftet als weiße Bereiche in der rechten unteren Raumecke

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Mathematische Modellbildung' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Mathematische%20Modellbildung/Themen/Corona-Modellierung/Zyklus%201%20Teilprojekt%201
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.