Diskrete und stetige Wahrscheinlichkeitsverteilungen

Einführung

Die Unterscheidung von diskrete und stetigen Wahrscheinlichkeitsverteilungen erfolgt über die Verteilungsfunktion. Der bereits aus der Analysis bekannte Begriff der Stetigkeit wird dabei auf die Verteilungsfunktion angewendet und stetige Wahrscheinlichkeitsverteilung besitzen eine stetige Verteilungsfunktion. Diskrete Verteilungen besitzen anschaulich Verteilungsfunktionen, die rechtsseitig stetige Treppenfunktionen bilden.

Beispiel - stetige Verteilung

Beispiele für Verteilungsfunktionen von Normalverteilungen mit unterschiedlichen Varianzen und Erwartungswerten.

Weder stetig noch diskret

Es gibt (eher unüblich) Wahrscheinlichkeitsverteilungen, die weder diskret noch stetig sind.

Einführendes Beispiel - diskret

Wir betrachten ein Würfelexperiment mit den möglichen Ergebgnissen $\Omega =\{1,2,3,4,5,6\}$ . Ein Ereignis kann man in Worten z.B. mit Ereignis A "gerade Zahl gewürfelt" oder Ereignis B "Zahl kleiner 5 gewürfelt" beschreiben. Solche Ereignisse sind formal Teilmengen von der Menge aller Ergebnisse $\Omega$ also $A=\{2,4,6\}\subseteq \Omega$ bzw. $B=\{1,2,3,4\}\subseteq \Omega$ . Jedem Ereignis wird dann ein Wahrscheinlichkeit $P(A)={\frac {3}{6}}$ bzw. $P(B)={\frac {4}{6}}$ zugeordnet.

Einführendes Beispiel - stetig

Eine Person wirft Dartscheibe und versucht dabei immer das den Mittelpunkt des Kreises (Bulls Eye) zu treffen. Die in Regel unbekannte Trefferverteilung auf der Dartscheibe ist eine stetige Wahrscheinlichkeitsverteilung auf einer Teilmenge $D\subset \mathbb {R} ^{2}$ .

Diskrete Wahrscheinlichkeitsräume

Eine diskrete (Wahrscheinlichkeits-)verteilung bzw. ein diskretes Wahrscheinlichkeitsmaß ist ein spezielles Wahrscheinlichkeitsmaß in der Stochastik. Im Gegensatz zu den allgemeinen Wahrscheinlichkeitsmaßen sind die diskreten Wahrscheinlichkeitsverteilungen auf einer endlichen bzw. abzählbaren Menge $M\subseteq \Omega$ von Ereignissen mit positiver Wahrscheinlichkeit ( $P(\{\omega \})>0$ für alle $\omega \in M$ ) und $P(M)=1$ definiert (siehe Wikipedia: Ereignis (Wahrscheinlichkeitstheorie)).

Weder stetig noch diskret - Summe der Wahrscheinlichkeiten von Einpunktmenge

Wahrscheinlichkeitsverteilungen, die weder diskret noch stetig sind, kann man bei abzählbarem Träger an der Summe der Wahrscheinlichkeiten von Einpunktmengen ablesen. Mit Menge $M\subseteq \Omega$ von Ereignissen mit positiver Wahrscheinlichkeit ( $P(\{\omega \})>0$ wäre $0<P(M)<1$ ein Verteilung, die weder diskret noch stetig ist.

Allgemeine Wahrscheinlichkeitsräume

Im Gegensatz zu endlichen bzw. abzählbaren Trägermengen $\Omega$ sind überabzählbare Grundmengen $\Omega$ problematisch, um jeder Teilmenge von $\Omega$ (Ereignissen) eine Wahrscheinlichkeit zuzuordnen. Z.B. auf dem Intervall $[0,1]\subset \mathbb {R}$ der reellen Zahlen treten Paradoxien auf. Der Satz von Vitali zeigt, dass die Potenzmenge von $\Omega$ nicht geeignet ist als Definitionsbereich des W'Maßes und man zu einem komplexeren Mengensystem, wie der Borelschen σ-Algebra übergehen muss.

Wahrscheinlichkeitsraum

Sei $(\Omega ,{\mathcal {S}})$ ein Messraum und eine Abbildung $P:{\mathcal {S}}\longrightarrow \mathbb {R}$ gegeben, die folgende Eigenschaften besitzt:

(Positivität) $P(A)\geq 0$ für alle $A\in \Omega$
(Normiertheit) $P(\Omega )=1$
( $\sigma$ -Additivität) $A_{n}\in {\mathcal {S}}$ für alle $n\in \mathbb {N}$ und paarweise disjunkt folgt: $P\left(\bigcup _{n\in \mathbb {N} }A_{n}\right)=\sum _{n\in \mathbb {N} }P\left(A_{n}\right)$ .

$P$ nennt man dann Wahrscheinlichkeitsmaß auf $(\Omega ,{\mathcal {S}})$ und $(\Omega ,{\mathcal {S}},P)$ Wahrscheinlichkeitsraum.

Bemerkung

Die Einschränkung 'paarweise disjunkt' ist wesentlich. Für die nicht paarweise disjunkte Mengen sieht man an folgenden Beispielen unmittelbar, dass die $\sigma$ -Additivität hier nicht gilt:

$A_{1}=A_{2}=\Omega$ und man erhält $1=P(\Omega )=P(A_{1}\cup A_{2})\not =P(A_{1})+P(A_{2})=2$ .
$A_{i}=\Omega$ gilt: $P(\bigcup _{i=1}^{\infty }A_{i})=1\not =\sum _{i=1}^{\infty }P(A_{i})=\infty$ .

Elementare Eigenschaften von P (1)

Allein aus der obigen Definition heraus leiten wir ab:

$P(\varnothing )=0$ , denn es folgt für alle $A_{i}=\varnothing$ : $P(\varnothing )=\sum _{i=1}^{\infty }P(\varnothing )$ ; die Ausnahme $P(\varnothing )>0$ liefert den Widerspruch.

$P(\bigcup _{i=1}^{n}A_{i})=\sum _{i=1}^{n}P(A_{i})$ für paarweise disjunkte $A_{1},...,A_{n}$ ('Additivität'). Insbesondere: $P(A\cup B)=P(A)+P(B)$ für disjunkte $A,B$ , denn setzte: $A_{n+1}=A_{n+2}=...=\varnothing$ und beachte 1).

Elementare Eigenschaften von P (2)

$P({\bar {A}})=1-P(A)$ , denn $1=P(\Omega )=P(A\cup {\bar {A}})=P(A)+P({\bar {A}})$ .
$P(A)\leq P(B)$ für $A\subset B$ ('Monotonie'), denn $B=B\cap {\bar {A}}\cup A$ (disjunkt), also $P(B)=P(A)+P(B\cap {\bar {A}})\geq P(A)$ .
Zusätzlich gilt $P(B\setminus A)=P(B)-P(A\cap B)$ mit $B\setminus A\equiv B\cap {\bar {A}}$ .
Es gilt außerdem $P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Allgemein: $P(A_{i},...,A_{n})\leq \sum _{i=1}^{n}P(A_{i})$
Insbesondere: $P(A\cup B)\leq P(A)+P(B)$

Elementare Eigenschaften von P (3)

Für einelementige (Elementar-)Ereignisse $\lbrace w\rbrace$ setzten wir $p_{w}=P(\lbrace w\rbrace )$ und haben somit:

$p_{w}\geq 0$ .
$\sum _{w\in \Omega }p_{w}=P(\Omega )=1$ .
$\sum _{w\in A}p_{w}=P(A)$ für jedes $A\in \Omega$ .

Aus Letzerem folgt, dass die Wahrscheinlichkeitsverteilung $P$ durch die Werte von $p_{w}$ eindeutig festgelegt werden kann.

Diskreter W'Raum - Münzwurf

Einfachstes Beispiel einer diskreten Wahrscheinlichkeitsverteilung wäre ein Wurf mit einer möglicherweise gezinkten Münze: Die Wahrscheinlichkeitsverteilung ordnet dem Ereignis "Die Münze zeigt Kopf" eine Zahl zu, die der Wahrscheinlichkeit entspricht, dass die Münze Kopf zeigt. Ebenso ordnet sie dem Ergebnis "Die Münze zeigt Zahl" eine Zahl zu, die der Wahrscheinlichkeit entspricht, dass die Münze Zahl zeigt. Dem intuitiven Verständnis von Wahrscheinlichkeit entsprechend summieren sich diese Zahlen zu eins auf.

Definition: Diskrete W'Verteilung

Eine Wahrscheinlichkeitsverteilung $(\Omega ,{\mathcal {S}},P)$ heißt diskrete Wahrscheinlichkeitsverteilung, wenn einer der folgenden drei Fälle gilt:

Sie ist auf einer endlichen Menge $\Omega$ definiert.
Sie ist auf einer abzählbar unendlichen Menge $\Omega$ definiert (z.B. den natürlichen Zahlen $\mathbb {N}$ )
Es gibt eine höchstens abzählbar Menge $\Omega _{0}\subset \Omega$ mit $P(\Omega _{0})=1$

Zufallsvariablen, deren Verteilung eine diskrete Wahrscheinlichkeitsverteilung ist, werden auch als diskrete Zufallsvariablen bezeichnet.

Beispiel: Münzwurf

Beispiel für die Definition auf einer endlichen Menge ist das Eingangs genannte Beispiel mit dem Münzwurf. Dieses wird auf der Menge $\{\operatorname {Kopf} ,\operatorname {Zahl} \}$ definiert und ist im fairen Fall gegeben durch

P(\{\operatorname {Kopf} \})={\frac {1}{2}}=P(\{\operatorname {Zahl} \}).

Häufig werden die Seiten der Münze auch kodiert, wie Kopf=1, Zahl=0 oder Kopf=K, Zahl=Z. Die Kodierung ändert dabei nichts an der Eigenschaft der Verteilung, diskret zu sein.

Beispiel: Poisson-Verteilung

Typisches Beispiel einer Wahrscheinlichkeitsverteilung auf einer abzählbar unendlichen Menge, genauer auf $\mathbb {N} _{0}$ ist die Poisson-Verteilung. Sie wird für einen reellen Parameter $\lambda >0$ definiert durch

P_{\lambda }(\{k\})={\frac {\lambda ^{k}}{k!}}\,\mathrm {e} ^{-\lambda }\,{\text{ für }}\,k\in \mathbb {N} _{0}.

Die Normiertheit einer Wahrscheinlichkeitsverteilung folgt hier aus der Definition der Exponentialfunktion über die Potenzreihe.

Aufgabe: Würfeln bis zu ersten 6

Welche Wahrscheinlichkeit hat das Ereignis A="Nach dem 5. Wurf eine 6 gewürfelt"? Welchem Fall einer diskreten Wahrscheinlichkeitsverteilung ist diese Beispiel zugeordnet?

Faltung

Beide obigen Beispiele können auch als diskrete Wahrscheinlichkeitsverteilungen auf dem Grundraum $\mathbb {R}$ aufgefasst werden. Dies ermöglicht beispielsweise das Definieren einer Verteilungsfunktion und erlaubt die Faltung der Wahrscheinlichkeitsverteilungen mit weiteren Wahrscheinlichkeitsverteilungen.

Konstruktion 1 - Wahrscheinlichkeitsfunktionen

Diskrete Wahrscheinlichkeitsverteilungen werden meist mittels Wahrscheinlichkeitsfunktionen definiert. Im Falle des Grundraumes $\mathbb {N} _{0}$ sind dies Funktionen $f$ , die jeder natürlichen Zahl $k$ eine positive, reelle Zahl zwischen null und eins zuordnen. Alle diese reellen Zahlen müssen sich zu eins aufsummieren. Dann setzt man

P(\{k\})=f(k).

Konstruktion 2 - Poisson-Verteilung

Im obigen Beispiel der Poisson-Verteilung wäre zum Beispiel

f(k)={\frac {\lambda ^{k}}{k!}}\,\mathrm {e} ^{-\lambda }.

Dieses Verfahren lässt sich für beliebige diskrete Wahrscheinlichkeitsverteilungen verwenden. Tatsächlich sind die diskreten Wahrscheinlichkeitsverteilungen genau diejenigen Verteilungen, die sich über eine Wahrscheinlichkeitsfunktion definieren lassen. Die Zuordnung diskrete Wahrscheinlichkeitsverteilung – Wahrscheinlichkeitsfunktion ist also bijektiv.

Definition - Wahrscheinlichkeitsfunktion

Eine Abbildung $p:\Omega \to [0,1];w\to p_{w}$ mit der Eigenschaft ('Normierung')

\sum _{w\in \Omega }p_{w}=1

heißt Wahrscheinlichkeitsfunktion (oder diskrete Wahrscheinlichkeitsdichte oder Zähldichte). Jede Wahrscheinlichkeitsfunktion $p$ legt eine Wahrscheinlichkeitsverteilung $P$ eindeutig fest ( $\sigma$ -Additivität von $P$ folgt dann aus dem "Umordnungssatz" für absolut konvergente Reihen). Meistens gibt man eine Wahrscheinlichkeitsverteilung durch eine Wahrscheinlichkeitsfunktion an.

Verteilungsfunktionen

In dem folgenden Abschnitt werden Verteilungsfunktionen behandelt. Die Begriffsdefinition ist notwendig, um stetige Wahrscheinlichkeitsverteilungen zu definieren. Unterschieden werden dabei

der eindimensionale Fall $\mathbb {R}$ und
der mehrdimensionale Fall $\mathbb {R} ^{n}$ .

Verteilungsfunktion - eindimensional

Bei reellwertigen Zufallsgrößen $X:\Omega \to \mathbb {R}$ wird die Verteilungsfunktion über die induzierte Verteilung auf $(\mathbb {R} ,{\mathcal {B}})$ über $F(x):=P^{X}((-\infty ,x])$ angegeben.

Verteilungsfunktion - mehrdimensional

Bei Zufallsgrößen $X:\Omega \to \mathbb {R} ^{n}$ wird die Verteilungsfunktion über die induzierte Verteilung auf $(\mathbb {R} ^{n},{\mathcal {B}}^{n})$ über $F(x_{1},\ldots ,x_{n}):=P^{X}((-\infty ,x_{1}]\times \cdots \times (-\infty ,x_{n}])$ angegeben.

Stetige Wahrscheinlichkeitsverteilungen

Bei stetigen Wahrscheinlichkeitsverteilung ist die Verteilungsfunktions stetig. Daraus ergibt sich insbesondere, dass kEinpunktmengen im Gegensatz zu den diskrete Verteilungen keine Wahrscheinlichkeitsmasse tragen. Es ist wichitg zu bemerken, dass sich der Stetigkeitsbegriff nicht auf die Wahrscheinlichkeitsdichte bezieht. Die Rechteckverteilung ist eine stetige Wahrscheinlichkeitsverteilung, dessen Dichtefunktion nicht stetig ist.

Definition - Stetige Verteilung

Eine Verteilung auf $(\mathbb {R} ^{n},{\mathcal {B}}^{n}),P$ heißt stetig, wenn die zugehörige Verteilungsfunktion $F:\mathbb {R} ^{n}$ stetig ist.

Bemerkung 1 - Stetige Verteilung

Die Definition liefert aber nicht, dass eine unstetige Verteilung eine diskrete Verteilung ist. Diskrete Verteilung sind rechtsseitig stetige monoton steigende Treppenfunktionen.

Bemerkung 2 - Stetige Verteilung

Die Definition liefert ebenfalls nicht, dass eine stetige Verteilungen eine stetige Wahrscheinlichkeitsdichte. Die Rechteckverteilung ist eine stetige Verteilung, aber diese besitzt keine stetige Wahrscheinlichkeitsdichte.

Beispiel - stetige Verteilung

Die folgende Abbildung zeigt verschieden Wahrscheinlichkeitsdichten der Normalverteilung

Verteilungsfunktion (1)

Die Abbildung zeigt eine Verteilungsfunktion einer Bernoulli-Verteilung zum Parameter $p=0{,}65$ mit charakteristischen Sprungstellen bei 0 und bei 1.

Verteilungsfunktion (2)

Bettet man diskrete Verteilungen auf $\mathbb {N}$ (oder einer beliebigen höchstens abzählbaren Teilmenge der reellen Zahlen) in die reellen Zahlen $\mathbb {R}$ ein, so kann der Verteilung eine Verteilungsfunktion zugeordnet werden. Diese zeichnet sich bei diskreten Wahrscheinlichkeitsverteilungen dadurch aus, dass sie stückweise konstant ist. An einer Stelle $i$ mit $P(\{i\})>0$ besitzt die Verteilungsfunktion immer einen „Sprung“ nach oben, und das um genau den Wert $P(\{i\})$ .

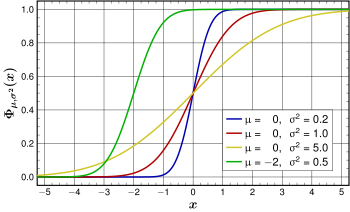
Beispiel - stetige Verteilungsfunktion

Die folgende Abbildung zeigt unterschiedliche Verteilungsfunktionen der Normalverteilung.

Wahrscheinlichkeitserzeugende Funktion

Diskreten Wahrscheinlichkeitsverteilungen auf $\mathbb {N} _{0}$ kann zusätzlich zu den klassischen erzeugenden Funktionen (Momenterzeugende Funktion, Kumulantenerzeugende Funktion und Charakteristische Funktion) noch eine wahrscheinlichkeitserzeugende Funktion zugeordnet werden. Dabei handelt es sich um ein Polynom oder um eine Potenzreihe, die jeder Wahrscheinlichkeitsverteilung eindeutig zugeordnet werden kann. Wahrscheinlichkeitserzeugende Funktionen erleichtern beispielsweise das Berechnen der Momente wie Erwartungswert oder Varianz oder liefern einfache Faltungsidentitäten.

Aufgabe - Weder stetig noch diskret

Konstruieren Sie eine Wahrscheinlichkeitsverteilung auf $(\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))$ , bei der

$P(\{-1\})={\frac {1}{2}}$
$P([0,1])={\frac {1}{2}}$ mit stetiger Gleichverteilung.

Skizzieren Sie die Verteilungsfunktion von $(P,\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))$ !

Spezielle diskrete Wahrscheinlichkeitsverteilungen

Folgend sind einige wichtige diskrete Wahrscheinlichkeitsverteilungen und ihre Konstruktion aufgezählt. Die Einteilung ist dabei nicht zwingend, manche Verteilungen können auch auf mehrere Arten konstruiert werden.

Aus der Bernoulli-Verteilung abgeleitet (1)

Ein Ausgangspunkt der Modellierung ist die Bernoulli-Verteilung. Sie modelliert den Wurf einer Münze, wobei "Kopf" mit 1 codiert wird und "Zahl" mit 0. Die Wahrscheinlichkeit für "Kopf" wird durch eine Zahl $p\in [0,1]$ gegeben. Somit handelt es sich um eine diskrete Wahrscheinlichkeitsverteilung auf $\{0,1\}.$

Aus dieser Verteilung lassen sich direkt ableiten:

Aus der Bernoulli-Verteilung abgeleitet (2)

Die Binomialverteilung: Sie gibt die Wahrscheinlichkeit an, bei $n$ unabhängigen Würfen mit derselben Münze $k$ Erfolge zu erhalten. Ihre multivariate Entsprechung ist die Multinomialverteilung.
Die Verallgemeinerte Binomialverteilung: Sie gibt die Wahrscheinlichkeit an, bei $n$ unabhängigen Würfen mit unterschiedlichen Münzen $k$ Erfolge zu erhalten.
Die Geometrische Verteilung: Sie gibt die Wahrscheinlichkeit für die Wartezeit auf den ersten Erfolg beim sukzessiven, unabhängigen Werfen einer Münze an.
Die Negative Binomialverteilung: Sie gibt die Wahrscheinlichkeit für die Wartezeit auf den $r$ -ten Erfolg beim sukzessiven, unabhängigen Werfen einer Münze an.

Aus der Bernoulli-Verteilung abgeleitet (3)

Dabei werden geometrische und negative Binomialverteilung auch in verschiedenen Varianten definiert.
Weitere ableitbare Wahrscheinlichkeitsverteilungen sind die Beta-Binomialverteilung (die Erfolgswahrscheinlichkeit der Münze selbst wird als Betaverteilt angenommen) sowie die Rademacher-Verteilung und die Zweipunktverteilung (Bernoulli-Verteilungen auf speziellen Werten) und die Dirac-Verteilung (degeneriertet Grenzfall einer Münze, die immer dasselbe Ergebnis zeigt).

Aus dem Urnenmodell abgeleitet (1)

Ein weiterer Ausgangspunkt der Modellierung ist das Urnenmodell, das auf der diskreten Gleichverteilung basiert. Dabei werden insgesamt $N$ Kugeln in mehrere Gruppen geteilt (gefärbt, nummeriert, etc.), in eine Urne gelegt. Aus dieser wird dann gezogen, entweder mit zurücklegen oder ohne. Dabei soll (entsprechend der Gleichverteilung) jede Kugel gleich wahrscheinlich sein. So lassen sich beispielsweise konstruieren:

Aus dem Urnenmodell abgeleitet (2)

die Hypergeometrische Verteilung: Sie gibt die Wahrscheinlichkeit an, bei $n$ -maligem Ziehen ohne Zurücklegen aus einer Urne mit zwei Sorten Kugeln genau $k$ Kugeln einer Sorte zu erhalten.
ihr multivariates Pendant, die multivariate hypergeometrische Verteilung.

Gleichverteilung (Definition) (1)

Die Gleichverteilung über einer endlichen Grundmenge $\Omega$ wird bestimmt durch die Wahrscheinlichkeitsfunktion

p_{w}={\frac {1}{|\Omega |}}

(für alle

w\in \Omega ).

Die Wahrscheinlichkeit für ein Ereignis $A\subset \Omega$ ist dann

P(A)=\sum _{w\in A}p_{w}={\frac {|A|}{|\Omega |}}.

Gleichverteilung (Definition) (2)

Die Gleichverteilung wird auch Laplaceverteilung genannt. Ein Zufallsexperiment, dem die Gleichverteilung zugeordnet wird, wird auch Laplaceexperiment genannt.
Interpretation der zweiten Formel: Sei $A\subset \Omega$ gegeben. Ein Ereignis $w\in A$ heißt "günstig" für $A$ . Jedes $w\in \Omega$ ist "möglich". ${\frac {|A|}{|\Omega |}}$ ist dann die Anzahl der günstigen durch die Anzahl der möglichen Ereignisse.

Gleichverteilung (Beispiel)

Einmal werfen mit einem symmetrischen Würfel. Auf $\Omega =\lbrace 1,2,...,6\rbrace$ definiert man die Wahrscheinlichkeitsfunktion $p_{1}=p_{2}=...=p_{6}={\frac {1}{6}}$ ("Gleichverteilung" über $\lbrace 1,2,...,6\rbrace$ ).

Ist $A=\lbrace 1,3,5\rbrace$ das Ereignis "ungerade Augenzahl", so gilt $P(A)=p_{1}+p_{3}+p_{5}={\frac {3}{6}}={1}{2}$ .

Einpunktverteilung (Beispiel)

Seien $\Omega$ und $w_{0}\in \Omega$ beliebig. Dann definiert

p_{w_{0}}=1,p_{w}=0

(für alle $w\neq w_{0}$ , "Einpunktverteilung") die in $w_{0}$ konzentrierte Wahrscheinlichkeitsverteilung $\epsilon _{w_{0}}$ . Es ist

\epsilon _{w_{0}}(A)=\left\{{\begin{array}{ll}0,&w_{0}\notin A\\1,&w_{0}\in A\end{array}}\right..

Geometrische Verteilung (Beispiel) (1)

Eine symmetrische Münze wird so oft geworfen, bis zum ersten Mal Kopf auftritt. Der Ergebnisraum $\Omega$ besteht aus allen möglichen auftretenden Sequenzen:

$w_{1}=K,w_{2}=ZK,w_{3}=ZZK...,w_{\infty }=ZZZZZ...$

(Wir schreiben $p_{k}$ anstatt $p_{w_{k}}$ .) Es ist $p_{1}={\frac {1}{2}}$ . Heuristische Überlegung zur Bestimmung der $p_{k},k>1$ :

Geometrische Verteilung (Beispiel) (2)

Wir betrachten $w_{k}=(Z...ZK)$ (k-1-mal Z) als Element der Menge $\Omega _{k}=\lbrace Z,K\rbrace ^{k}$ . Es ist $|\Omega _{k}|=2^{k}$ . Alle $2^{k}$ Elemente von $\Omega _{k}$ sind gleichwahrscheinlich. Es folgt:

p_{k}={\frac {1}{2^{k}}},k\in \mathbb {N}

('Geometrische Verteilung')

Normierung: $\sum _{k=1}^{\infty }p_{k}=\sum _{k=1}^{\infty }{\frac {1}{2^{k}}}=1$ . Somit hat man also $p_{\infty }=0$ zu setzen.

Siehe auch

Literatur

Hans-Otto Georgii: Stochastik. Einführung in die Wahrscheinlichkeitstheorie und Statistik. 4. Auflage. Walter de Gruyter, Berlin 2009, doi:10.1515/9783110215274
Klaus D. Schmidt: Maß und Wahrscheinlichkeit. 2., durchgesehene Auflage. Springer-Verlag, Heidelberg Dordrecht London New York 2011, doi:10.1007/978-3-642-21026-6
David Meintrup, Stefan Schäffler: Stochastik. Theorie und Anwendungen. Springer-Verlag, Berlin Heidelberg New York 2005, S. 90, doi:10.1007/b137972

Seiten-Information

Der Foliensatz wurde für den Kurs:Stochastik mit Wiki2Reveal über den Linkgenerator erstellt.

Inhalte der Seite basieren auf:
- https://de.wikipedia.org/wiki/Diskrete_Wahrscheinlichkeitsverteilung
Diese Seite ist eine PanDocElectron-SLIDE Dokumententyp
Quelle: Wikiversity DE https://de.wikiversity.org/wiki/Normen,_Metriken,_Topologie
siehe Wiki2Reveal zur Funktionsweise von Wiki2Reveal.