Kurs:Maßtheorie auf topologischen Räumen/Differenzierbarkeit in Analysis und Funktiontheorie
Einführung
[Bearbeiten]Bevor die Differenzierbarkeit allgemein auf topologischen Vektorräumen zu definieren, betrachten den Begriff der Differenzierbarkeit aus der Analysis und erweitern diesen dann auf topologische Vektoräume.
Differenzierbarkeit in der reellen Analysis
[Bearbeiten]Als Differenzierbarkeit bezeichnet man in der Mathematik die Eigenschaft einer Funktion, sich lokal um einen Punkt in eindeutiger Weise linear approximieren zu lassen.

Differenzierbarkeit mit mehreren Veränderlichen
[Bearbeiten]Der Begriff Differenzierbarkeit ist nicht nur für reellwertige Funktionen auf der Menge der reellen Zahlen erklärt, sondern auch für Funktionen mehrerer Variablen, für komplexe Funktionen, für Abbildungen zwischen reellen oder komplexen Vektorräumen und für viele andere Typen von Funktionen und Abbildungen. Für manche Typen von Funktionen (zum Beispiel für Funktionen mehrerer Variablen) gibt es mehrere verschiedene Differenzierbarkeitsbegriffe.
Thematische Einordnung der Differenzierbarkeit
[Bearbeiten]Die Frage nach der Differenzierbarkeit gehört zu den Problemstellungen der Differentialrechnung, eines Teilgebiets der Analysis. In diesem Kurs wird Differenzierbarkeit auf unitalen topologischen Algebren mit einem unital positiven Gaugefunktionalsystem betrachtet.
Reellwertige Funktionen einer reellen Veränderlichen
[Bearbeiten]Definitionen
[Bearbeiten]
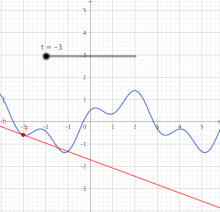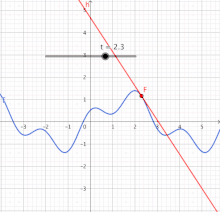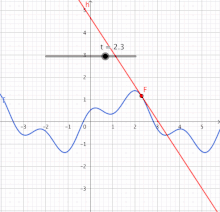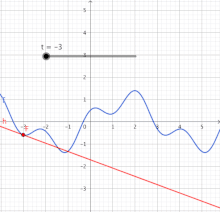
Rot: Graph der linearen Funktion g, die f in der Nähe der Stelle x0 approximiert


Im einfachsten Fall betrachtet man eine reellwertige Funktion einer reellen Variablen, also eine Funktion , deren Funktionswerte reelle Zahlen sind und deren Definitionsbereich ein offenes Intervall reeller Zahlen ist. Eine solche Funktion ist differenzierbar an einer Stelle aus ihrem Definitionsbereich, wenn die Ableitung von an dieser Stelle existiert. Es gibt im Wesentlichen zwei äquivalente Definitionen für die Existenz der Ableitung:
1. Definition: Grenzwert Differenzenquotient
[Bearbeiten]Eine Funktion ist genau dann differenzierbar an der Stelle ihres Definitionsbereichs, wenn der beidseitige Grenzwert der Differenzenquotienten
existiert. Diesen Grenzwert bezeichnet man als die Ableitung von an der Stelle , geschrieben .
2. Definition: Taylorentwicklung bis zur 1. Ableitung
[Bearbeiten]Eine Funktion ist genau dann differenzierbar an der Stelle ihres Definitionsbereichs, wenn eine reelle Zahl (die von abhängen darf) und eine (ebenfalls von abhängige) Funktion (Fehler der Approximation) mit folgenden Eigenschaften existieren:
- Für geht schneller als linear gegen 0, das heißt:
Bemerkung zur Taylorentwicklung
[Bearbeiten]Die Funktion lässt sich also in der Nähe von durch eine lineare Funktion mit
bis auf den Fehler approximieren. Den Wert bezeichnet man als die Ableitung von an der Stelle .
Bemerkung zur Geschichte der Definition
[Bearbeiten]Differenzierbare Funktionen sind damit genau diejenigen Funktionen, die sich lokal durch lineare Funktionen approximieren lassen (siehe Abbildung). Diese Definition geht auf Karl Weierstraß zurück und wird Weierstraßsche Zerlegungsformel genannt.
Definition: Differenzierbare Funktion
[Bearbeiten]Eine Funktion heißt genau dann differenzierbar (ohne Einschränkung auf einen speziellen Punkt), wenn sie an jeder Stelle ihres Definitionsbereichs differenzierbar ist. Die Funktion ordnet jedem und die Ableitung zu. heißt dann Ableitungsfunktion oder kurz Ableitung von .
Erläuterungen 1 - Steigung der Tangente
[Bearbeiten]Grafisch lässt sich die Eigenschaft Differenzierbarkeit so deuten, dass eine Funktion genau dann an der Stelle differenzierbar ist, wenn im zugehörigen Punkt des Graphen von genau eine Tangente existiert. Die Tangente ist der Graph, der in der 2. Definition genannten linearen Funktion mit:
Erläuterungen 2 - Steigung der Tangente - Steigung Sekante
[Bearbeiten]Die Ableitung von an der Stelle ist die Steigung dieser Tangente. Die in der ersten Definition genannten Differenzenquotienten sind die Steigungen von Sekanten durch den Punkt und einen anderen Kurvenpunkt . Die Funktion ist also an der Stelle differenzierbar, wenn die Steigungen dieser Sekanten beim Grenzübergang gegen die Steigung der Tangente konvergieren.
Erläuterungen 3 - Zusammenhang Stetigkeit und Differenzierbarkeit
[Bearbeiten]Aus Differenzierbarkeit folgt Stetigkeit: Jede an einer Stelle differenzierbare Funktion ist dort auch stetig. Jede auf ihrem Definitionsbereich differenzierbare Funktion ist stetig. Die Umkehrung gilt nicht. Die Betragsfunktion ist z.B. keine überall differenzierbaren Funktionen, obwohl diese an jeder Stelle stetig ist.
Beispiele für differenzierbare Funktionen
[Bearbeiten]Aus den Ableitungsregeln folgt:
- Jede Funktion, die sich durch ein Polynom darstellen lässt, ist differenzierbar.
- Summen, Produkte und Quotienten von differenzierbaren Funktionen sind differenzierbar.
- Verkettungen von differenzierbaren Funktionen sind differenzierbar.
Ableitung der Umkehrfunktion
[Bearbeiten]Die Umkehrfunktion einer bijektiven differenzierbaren Funktion ist genau dann an der Stelle differenzierbar, wenn ist.
Berechnung der Ableitung einer Funktion
[Bearbeiten]Die Parabelfunktion ist für alle differenzierbar. Sei dann ist
und ihre Ableitung ist .
Potenzreihen und Differenzierbarkeit
[Bearbeiten]Aus den Grenzwertsätzne für Potenzreihen folgt:
- Jede Funktion, die lokal durch eine Potenzreihe dargestellt werden kann, ist differenzierbar.
- In der komplexen Analysis liefert die einmalige komplexe Differenzierbarkeit (Holomorphie) auf einer offenen Menge auch, dass die Funktion unendlich oft differenzierbar ist. Damit lassen sich holomorphe Funktionen lokal in Potenzreihen entwickeln.
Beispiele für nicht differenzierbare Funktionen
[Bearbeiten]
Da jede differenzierbare Funktion stetig ist, ist umgekehrt jede unstetige Funktion (zum Beispiel eine Treppenfunktion oder die Dirichlet-Funktion) ein Beispiel für eine nicht differenzierbare Funktion. Es gibt aber auch Funktionen, die zwar stetig sind, aber nicht oder nicht überall differenzierbar.
Wurzelfunktion
[Bearbeiten]
Die Wurzelfunktion , ist an der Stelle nicht differenzierbar. Der Differenzenquotient
strebt für gegen unendlich, konvergiert also nicht. Der Graph der Funktion hat an der Stelle eine Tangente, diese verläuft aber vertikal und besitzt deshalb keine Steigung.
Betragsfunktion
[Bearbeiten]
Die Betragsfunktion ist an der Stelle nicht differenzierbar.
Für ist und damit
- .
Für ist dagegen und folglich
- .
Betragsfunktion - rechtsseitige und linksseitige Grenzwerte
[Bearbeiten]Da der links- und der rechtsseitige Grenzwert nicht übereinstimmen, existiert der Grenzwert nicht. Die Funktion ist somit an der betrachteten Stelle nicht differenzierbar.
Es existieren an der Stelle jedoch die rechtsseitige Ableitung
und die linksseitige Ableitung
- .
Anschauliche Beschreibung
[Bearbeiten]Der Funktionsgraph hat an der Stelle einen Knick. Es gibt sozusagen eine linksseitige Tangente mit Steigung und eine rechtsseitige mit Steigung . Zu jeder Steigung zwischen und gibt es eine Gerade, die den Funktionsgraph im Punkt „berührt“, aber sich nicht „anschmiegt“.
Dies ist ein typisches Verhalten für abschnittsweise definierte Funktionen, wo an den Nahtstellen zwar die Funktionswerte zusammenpassen, aber nicht die Ableitungen. Die Graphen von differenzierbaren Funktionen haben demgegenüber keine Knicke.
Beispiel - stetig - in einem Punkt nicht differenzierbar
[Bearbeiten]
Die Funktion
ist an der Stelle 0 stetig, aber nicht differenzierbar (aber überall sonst). Für den Differenzenquotient an der Stelle 0 gilt
Der Limes für existiert nicht. Es existieren auch keine einseitigen Grenzwerte. Vielmehr pendelt der Differenzenquotient, wenn gegen 0 geht, unendlich oft zwischen den Werten −1 und 1 und nimmt dabei jeden Zwischenwert unendlich oft an.
Weierstraß-Funktion - stetig - nirgends differenzierbar
[Bearbeiten]Die nach ihrem Entdecker benannte Weierstraß-Funktion
ist überall stetig, aber nirgends differenzierbar.
Wiener-Prozess
[Bearbeiten]Weitere Beispiele liefert die mathematische Brownsche Bewegung: Fast jeder Pfad eines Wiener-Prozesses ist als Funktion stetig, aber nirgends differenzierbar.

Stetige Differenzierbarkeit und höhere Ableitungen
[Bearbeiten]
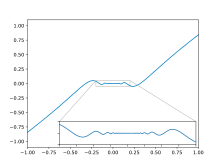
Eine Funktion heißt stetig differenzierbar, wenn sie differenzierbar ist und ihre Ableitung stetig ist. Selbst wenn eine Funktion überall differenzierbar ist, muss die Ableitung nicht stetig sein. Zum Beispiel ist die Funktion
an jeder Stelle, inklusive , differenzierbar
Differenzierbarkeit im Nullpunkt
[Bearbeiten]Die Funktion ist u.a. in 0 differenzierbar, weil
Ableitung im Nullpunkt nicht stetig
[Bearbeiten]Die Ableitung
ist aber an der Stelle 0 nicht stetig.
Definition: n-fache Differenzierbarkeit
[Bearbeiten]Eine Funktion heißt zweimal differenzierbar, wenn ihre Ableitungsfunktion differenzierbar ist. Entsprechend wird dreimal, viermal, …, -mal differenzierbar definiert. Die höheren Ableitungen werden mit , , , …, bezeichnet.
Differenzierbarkeit impliziert Stetigkeit
[Bearbeiten]Da aus der Differenzierbarkeit einer Funktion die Stetigkeit folgt, sind bei einer zweimal differenzierbaren Funktion die Funktion selbst und die erste Ableitung automatisch stetig. Die zweite Ableitung braucht jedoch nicht stetig zu sein. Entsprechend sind bei einer -mal differenzierbaren Funktion die Funktion selbst und alle Ableitungen , , … bis zur -ten Ableitung stetig. Für die -te Ableitung braucht dies jedoch nicht zu gelten. Ist diese auch stetig, so nennt man -mal stetig differenzierbar. Sind alle Ableitungen wieder differenzierbar, so nennt man die Funktion unendlich oft differenzierbar oder glatt.
Vektorraum von differenzierbaren Funktionen
[Bearbeiten]Sei ein Körper. bezeichnet die Menge aller -mal stetig differenzierbaren Funktionen mit der Definitionsmenge und dem Wertebereich . Die Menge der unendlich oft differenzierbaren Funktionen heißt . Eine -mal stetig differenzierbare Funktion nennt man daher auch Funktion der Differentiationsklasse , kurz: Funktion der Klasse oder -Funktion. Eine unendlich oft differenzierbare Funktion heißt entsprechend Funktion der (Differentiations-)Klasse oder -Funktion.
Beispiel 1 - einmal stetig differenzierbare Funktion
[Bearbeiten]Die Funktion
ist differenzierbar, ihre Ableitung ist die Funktion , die stetig, aber an der Stelle 0 nicht differenzierbar ist. Die Funktion ist also stetig differenzierbar, aber an der Stelle 0 nicht zweimal differenzierbar.
Beispiel 2 - k-fach stetig differenzierbare Funktion
[Bearbeiten]Entsprechend ist die Funktion
-mal stetig differenzierbar, aber an der Stelle 0 nicht -mal differenzierbar.
Komplexe Funktionen
[Bearbeiten]Für komplexe Funktionen, also komplexwertige Funktionen einer komplexen Variablen, definiert man Differenzierbarkeit ganz analog zu reellen Funktionen. Es sei eine offene Teilmenge der komplexen Ebene und ein Punkt dieser Teilmenge. Eine Funktion heißt komplex differenzierbar im Punkt , falls der Grenzwert
existiert.[1] In diesem Fall bezeichnet man diesen Grenzwert als .
Eine Funktion heißt holomorph im Punkt , falls eine Umgebung von existiert, in der komplex differenzierbar ist. Holomorphe Funktionen sind automatisch unendlich oft komplex differenzierbar und sogar analytisch.
Reellwertige Funktionen mehrerer Variablen
[Bearbeiten]Für Funktionen mehrerer Veränderlicher, also Funktionen, die auf offenen Teilmengen des euklidischen Raums definiert sind, gibt es mehrere verschieden starke Begriffe der Differenzierbarkeit. Im Folgenden sei eine offene Menge. Die Elemente des können als -Tupel geschrieben werden. Weiter sei eine Funktion gegeben. Wir betrachten einen festen Punkt und betrachten Differenzierbarkeit im Punkt .
Partielle Differenzierbarkeit
[Bearbeiten]Dies ist der schwächste Differenzierbarkeitsbegriff. Die Funktion heißt partiell differenzierbar am Punkt in Richtung , falls die partielle Ableitung
existiert. Man betrachtet also alle Variablen bis auf als konstant und betrachtet die so erhaltene Funktion einer Veränderlichen.
Die Funktion heißt partiell differenzierbar, wenn in jedem Punkt alle partiellen Ableitungen existieren. Sie heißt stetig partiell differenzierbar, falls alle partiellen Ableitungen stetige Funktionen von nach sind.
Bemerkung - partielle Differenzierbarkeit und Stetigkeit
[Bearbeiten]Aus partieller Differenzierbarkeit folgt nicht die Stetigkeit, sondern nur Stetigkeit in Richtung der Koordinatenachsen.
Richtungsableitung
[Bearbeiten]Ist ein Einheitsvektor, so ist die (beidseitige) Richtungsableitung von in Richtung an der Stelle definiert als
- .
Einseitige Richtungsableitung
[Bearbeiten]Betrachtet man nur positive , so erhält man die einseitige Richtungsableitung
- .
Die Funktion heißt (einseitig) differenzierbar in Richtung von , falls die (einseitige) Richtungsableitung von in Richtung existiert. Die Richtungsableitungen in Richtung der Einheitsvektoren der Standardbasis sind gerade die partiellen Ableitungen
- .
Bemerkung - Einseitige Richtungsableitung
[Bearbeiten]Die einseitigen Richtungsableitungen verallgemeinern den Begriff des rechtsseitigen und linksseitigen Grenzwertes für den Differenzenquotienten aus der elementaren Analysis mit eindimensionalem Definitionsbereich.
Totale Differenzierbarkeit
[Bearbeiten]Die Funktion heißt total differenzierbar im Punkt , falls eine lineare Abbildung und eine Funktion existieren, so dass sich bis auf den Fehler durch approximieren lässt,
und von höherer als erster Ordnung gegen 0 geht, das heißt für .
Totale Ableitung
[Bearbeiten]Die lineare Abbildung heißt totale Ableitung von im Punkt . Sie wird mit bezeichnet. Die Matrixdarstellung bezüglich der Standardbasis heißt Jacobi-Matrix und wird mit oder auch bezeichnet. Die Funktion heißt total differenzierbar, falls sie in jedem Punkt total differenzierbar ist.
Bemerkung - totale Differenzierbarkeit und Stetigkeit
[Bearbeiten]Eine total differenzierbare Funktion ist auch stetig.
In der neueren mathematischen Literatur spricht man statt von totaler Differenzierbarkeit meist einfach von Differenzierbarkeit. Die totale Ableitung wird auch Differential genannt.
Zusammenhänge zwischen den verschiedenen Differenzierbarkeitsbegriffen
[Bearbeiten]- Ist beidseitig differenzierbar in jede Richtung, so ist insbesondere partiell differenzierbar.
- Ist total differenzierbar, so ist differenzierbar in jede Richtung (also insbesondere auch partiell differenzierbar). Die Einträge der Jacobi-Matrix sind die partiellen Ableitungen
- .
- Man erhält die Richtungsableitung in Richtung , indem man die totale Ableitung (eine lineare Abbildung) auf den Vektor anwendet.
Umkehrungen ohne Stetigkeit der Ableitungen
[Bearbeiten]Die Umkehrungen gelten nicht:
- Aus der partiellen Differenzierbarkeit folgt weder die totale Differenzierbarkeit noch die beidseitige oder einseitige Differenzierbarkeit in Richtungen, die keine Koordinatenrichtungen sind.
- Auch aus der beidseitigen Differenzierbarkeit in alle Richtungen folgt nicht totale Differenzierbarkeit. Selbst dann nicht, wenn der Kandidat für die totale Ableitung, die Abbildung , linear ist.
Umkehrungen mit Stetigkeit der Ableitungen
[Bearbeiten]Anders ist es, wenn man nicht nur die Existenz, sondern auch die Stetigkeit der partiellen Ableitungen voraussetzt.
- Ist stetig partiell differenzierbar, so ist auch total differenzierbar.
Man nennt stetig partiell differenzierbare Funktionen deshalb auch einfach stetig differenzierbar. Auch hier gilt die Umkehrung nicht:
- Aus totaler Differenzierbarkeit folgt nicht die Stetigkeit der partiellen Ableitungen.
Implikationen für Differenzierbarkeitseigenschaften
[Bearbeiten]Insgesamt gilt somit:
- stetige partielle Differenzierbarkeit totale Differenzierbarkeit Differenzierbarkeit in jede Richtung partielle Differenzierbarkeit,
Es gelten jedoch keine der Umkehrungen.
Beispiele
[Bearbeiten]- Jede Funktion, die sich als Polynom in den Variablen darstellen lässt, ist stetig differenzierbar.
- Summen, Produkte, Quotienten und Verkettungen von stetig differenzierbaren Funktionen sind stetig differenzierbar.
Gegenbeispiele
[Bearbeiten]Alle Gegenbeispiele sind Funktionen auf dem . Die Koordinaten werden mit und bezeichnet statt mit und . Von Interesse ist hier nur die Differenzierbarkeit und Stetigkeit am Ursprung . Überall sonst sind die Funktionen stetig differenzierbar.
Partiell differenzierbar, aber nicht stetig und nicht alle Richtungsableitungen
[Bearbeiten]
Die Funktion
ist an der Stelle (0,0) partiell differenzierbar. Auf den Koordinatenachsen hat die Funktion konstant den Wert 0, das heißt für alle und gilt
- .
Daraus folgt
- .
Die Funktion ist jedoch bei (0,0) nicht stetig. Auf der ersten Winkelhalbierenden (mit Ausnahme des Ursprungs) hat konstant den Wert eins (). Nähert man sich dem Ursprung auf der ersten Winkelhalbierenden, so streben die Funktionswerte also gegen 1. Die Richtungsableitung in andere Richtungen als die der Koordinatenachsen existieren nicht.

Die Funktion
ist an der Stelle (0,0) partiell differenzierbar und stetig. Alle einseitigen Richtungsableitungen existieren, aber außer in die Koordinatenrichtungen nicht die beidseitigen.
Einseitige Ableitung - aber keine beidseitigen Richtungsableitungen
[Bearbeiten]
Die euklidische Norm
verallgemeinert die Betragsfunktion. Sie ist überall stetig.
Einseitige Richtungsableitung
[Bearbeiten]Für jeden Einheitsvektor existiert die einseitige Richtungsableitung von in und es gilt
Der Grenzwert existiert nur einseitig, also existieren die beidseitigen Richtungsableitungen nicht. Insbesondere ist die Funktion auch nicht partiell differenzierbar.
Alle Richtungsableitungen existieren, aber definieren keine lineare Abbildung
[Bearbeiten]
Hier existieren alle Richtungsableitungen, für die partiellen Ableitungen gilt
Die Abbildung ist jedoch nicht linear. Für den Einheitsvektor gilt
während
Alle Richtungsableitungen existieren und definieren eine lineare Abbildung, aber nicht total differenzierbar
[Bearbeiten]
Hier existieren alle Richtungsableitungen, für jeden Vektor gilt . Insbesondere ist partiell differenzierbar mit
und die Abbildung
ist die Nullabbildung, also trivialerweise linear.
Die Funktion ist auch stetig. Sie ist jedoch an der Stelle (0,0) nicht total differenzierbar. Wäre sie es, so wäre die Nullabbildung und für jeden Vektor gälte
- .
Für das Fehlerglied gälte also
- .
Setzt man und mit , so erhält man
- und , also .
Für gegen 0 geht dieser Term gegen statt gegen 0.
Total differenzierbar, aber nicht stetig partiell differenzierbar
[Bearbeiten]
Diese Funktion ist der entsprechenden Beispielfunktion einer Variablen nachgebildet, der Nachweis verläuft im Prinzip genauso wie dort.
Die Funktion ist an der Stelle (0,0) total differenzierbar, die Ableitung ist die Nullfunktion. Nähert man sich dem Nullpunkt, so divergieren jedoch die partiellen Ableitungen, zum Beispiel geht der Betrag von
gegen unendlich für gegen 0.
Abbildungen zwischen endlichdimensionalen Vektorräumen
[Bearbeiten]Eine Abbildung von einer offenen Menge in den Vektorraum lässt sich durch ihre Komponentenfunktionen darstellen:
- mit für .
Differenzierbarkeit von lässt sich dann auf Differenzierbarkeit der zurückführen. ist (im Punkt ) genau dann partiell differenzierbar (differenzierbar in Richtung des Vektors , total differenzierbar, stetig partiell differenzierbar), wenn alle Komponentenfunktionen diese Eigenschaft haben.
Jakobi-Matrix
[Bearbeiten]Ist im Punkt total differenzierbar, so ist eine lineare Abbildung von nach . Ihre Darstellungsmatrix, die Jacobi-Matrix, besteht aus den partiellen Ableitungen der Komponentenfunktion :
und die Richtungsableitung von im Punkt in Richtung ist das Bild des Vektors unter der linearen Abbildung .
Funktionen und Abbildungen auf unendlichdimensionalen Vektorräumen
[Bearbeiten]Auf unendlichdimensionalen Vektorräumen gibt es keine Koordinaten, deshalb gibt es keine partielle Differenzierbarkeit. Die Begriffe Richtungsableitung und totale Differenzierbarkeit lassen sich jedoch auf unendlichdimensionale Vektorräume verallgemeinern. Dabei spielt im Gegensatz zum Endlichdimensionalen die Topologie auf den Vektorräumen eine wichtige Rolle. Typische Beispiel für unendlichdimensionale Vektorräume sind Funktionenräume, also Vektorräume, deren „Vektoren“ Funktionen sind. Zur Unterscheidung nennt man die auf diesen Vektorräume definierten Funktionen Funktionale und nennt Abbildungen zwischen solchen Vektorräumen Operatoren.
Gâteaux-Differenzierbarkeit
[Bearbeiten]Der Richtungsableitung entspricht die Gâteaux-Ableitung. Gegeben sei ein normierter Vektorraum (das heißt ein (typischerweise unendlichdimensionaler) Vektorraum zusammen mit einer Norm ), eine offene Teilmenge und ein Funktional . Die Gâteaux-Ableitung von an einem „Punkt“ in Richtung eines Vektors ist dann gegeben durch
falls der Grenzwert existiert.
Bemerkung - Normierte Gateaux-Ableitung
[Bearbeiten]Der Wert der Ableitung ist in der Regel von der Länge von abhängig. Eine Normierung des Vektors mit mit entspricht der Normierung der partiellen Ableitung in Richtung der Einheitsvektoren. Im normierten Fall ergibt sich:
Aufgaben
[Bearbeiten]- Geben Sie eine Beispiel für eine Richtungsableitung an, bei dem sich die Richtungsableitung in Richtung und unterscheiden.
- Sei der Vektorraum der stetigen Funktionen mit der Maximumsnorm auf mit . Gegeben ist die Abbildung mit . Betrachten Sie die Gateaux-Ableitung von an der Stelle in Richtung mit und .
Gâteaux-Abbildung
[Bearbeiten]Falls die Gâteaux-Ableitung für jedes existiert, dann
ist eine Abbildung , erklärt.
Aus der Definition folgt sofort, dass diese Abbildung positiv homogen ist, also für alle .
Bemerkung - Existenz aller Richtungsableitungen
[Bearbeiten]Wie im Endlichdimensionalen folgt aus der Existenz aller Richtungsableitungen nicht, dass additiv und damit linear ist. Auch wenn die Abbildung linear ist, folgt nicht, dass sie stetig ist.
Bemerkung - Unterschiedliche nicht verträgliche Definitionen
[Bearbeiten]Für den Begriff Gâteaux-Differenzierbarkeit gibt es mehrere nicht verträgliche Konventionen:
Manche Autoren nennen ein Funktional Gâteaux-differenzierbar im Punkt , falls alle existieren, und bezeichnen dann die Abbildung als Gateaux-Ableitung von im Punkt . Andere fordern zusätzlich, dass linear und stetig ist.
Gâteaux-Differenzierbarkeit für Operatoren
[Bearbeiten]Ganz analog definiert man Gâteaux-Differenzierbarkeit und Gâteaux-Ableitung für Operatoren von einem normierten Vektorraum in einen andern normierten Vektorraum (typischerweise ein Banachraum). Die in der Definition der Gâteaux-Ableitung geforderte Konvergenz versteht sich dann im Sinne der Norm auf . Entsprechendes gilt für die Stetigkeit von .
Fréchet-Differenzierbarkeit
[Bearbeiten]Der totalen Differenzierbarkeit im Endlichdimensionalen entspricht bei unendlichdimensionalen Vektorräumen die Fréchet-Differenzierbarkeit. Gegeben seien Banachräume und , eine offene Teilmenge , eine Abbildung und ein Punkt .
Definition - Fréchet-differenzierbar
[Bearbeiten]Die Abbildung heißt Fréchet-differenzierbar, wenn eine beschränkte (also stetige) lineare Abbildung und eine Abbildung existieren, sodass für alle mit gilt
Dabei steht im Zähler die Norm von , im Nenner die von .
Bezeichung - Fréchet-Ableitung
[Bearbeiten]Der lineare Operator heißt in diesem Fall Fréchet-Ableitung von an der Stelle .
Zusammenhänge
[Bearbeiten]Wie im Endlichdimensionalen ist jede Fréchet-differenzierbare Abbildung auch Gâteaux-differenzierbar und die Gâteaux-Ableitung stimmt mit der Fréchet-Ableitung überein. Umgekehrt braucht im Punkt selbst dann nicht Fréchet-differenzierbar zu sein, wenn die Gâteaux-Ableitung linear und stetig ist.
Begriffserweiterungen
[Bearbeiten]Folgende Konzepte sind Verallgemeinerungen der Differenzierbarkeit:
- schwache Ableitungen
- Differenzierbarkeit im Sinne von Distributionen
- Radon-Nikodým-Ableitung
Weblinks
[Bearbeiten]![]() Wikibooks: Mathe für Nicht-Freaks: Ableitung und Differenzierbarkeit – Lern- und Lehrmaterialien
Wikibooks: Mathe für Nicht-Freaks: Ableitung und Differenzierbarkeit – Lern- und Lehrmaterialien
Einzelnachweise
[Bearbeiten]- ↑ Guido Walz (Hrsg.): Lexikon der Mathematik. 2. Auflage. Band 3 (Inp bis Mon). Springer Spektrum Verlag, Mannheim 2017, ISBN 978-3-662-53501-1, S. 148 f., doi:10.1007/978-3-662-53502-8.
Literatur
[Bearbeiten]Im Prinzip sämtliche einführende Literatur zu Analysis und/oder Differentialrechnung. Beispielsweise seien genannt:
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. 7. Auflage. Vieweg, Braunschweig 2004, ISBN 3-528-67224-2.
- Otto Forster: Analysis 2. Differentialrechnung im Rn. Gewöhnliche Differentialgleichungen. 6. Auflage. Vieweg, Braunschweig 2005, ISBN 3-528-47231-6.
- Konrad Königsberger: Analysis. 2 Bände. Springer, Berlin 2004, ISBN 3-540-41282-4.
Seiteninformation
[Bearbeiten]Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Wiki2Reveal
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Maßtheorie auf topologischen Räumen' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Ma%C3%9Ftheorie%20auf%20topologischen%20R%C3%A4umen/Differenzierbarkeit%20in%20Analysis%20und%20Funktiontheorie
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.
Wikipedia2Wikiversity
[Bearbeiten]Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:


























































































































































































![{\displaystyle V:={\mathcal {C}}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ba935781730b6339df9ea4dd1ed187114eb53e7)
![{\displaystyle \|f\|:=\displaystyle \max _{x\in [a,b]}|f(x)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c7744a91410917cb2532204acd99b5f8007ad80)























