Untersuchen der Luftqualität in Klassenräumen im Hinblick auf die Sitzordnung
- im ersten Lockdown (März 2020) Schließungen von jeglichen Bildungseinrichtungen
- Präsenzunterricht soll nicht mehr ausfallen
- deshalb mittlerweile (seit Juni 2020) Hygiene-Konzepte, die neben den AHA-Regeln auch regelmäßiges Lüften vorsehen
- ⇒ relevantes Thema in der aktuellen Situation
Fragestellung der Modellierung:
- Wie gut werden verschiedenen Raumpunkte und Bereiche in einem Klassenzimmer gelüftet und was bedeutet dies für die Sitzordnung?
Bezug zur Mathematik
- Modellierung auf verschiedenen Niveaus:
- Sekundarstufe 1: elementare Geometrie
- Sekundarstufe 2: analytische Geometrie
- Universität: mehrdimensionale Analysis
- verwendete Programme: Geogebra, Maxima
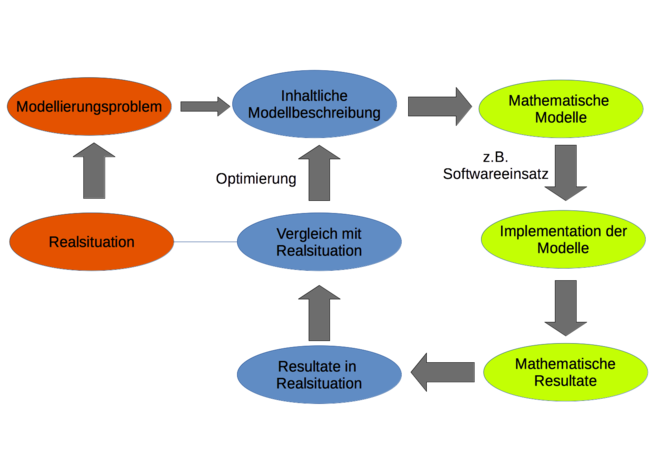
Modellierungszyklus auf Universitätsniveau
[Bearbeiten]- Ziel: Anordnung der Sitzplätze im Klassenzimmer in Abhängigkeit der Lüftungsqualität
- ⇒ neuer Schwerpunkt mit stärkerem Anwendungsbezug
- Lüftungsgütefunktion wird entsprechend der Vorgehensweise aus Modellierungszyklus 2 aufgestellt
- Betrachtung der Punkte der Form

- Aufstellen von vier Geradengleichungen, die die Trägergeraden der Lüftungsstrecken sind
- Bestimmung der Lotfußpunkte des Punktes und der Geraden
- Der Abstand zwischen den Lotfußpunkten und dem beliebigen Raumpunkt wird ermittelt
- Außerdem wird ein Term berechnet, der den Abstand zwischen den Mittelpunkten der Fenster und
 darstellt.
darstellt.
- Abstände werden anschließend mithilfe einer Glockenkurve normiert und für jede Lüftungsstrecke addiert
 und
und 
 Überarbeitetes 3D Modell zur Bewertung der Luftqualität im Klassenzimmer - https://www.geogebra.org/classic/sd7cj7x4
Überarbeitetes 3D Modell zur Bewertung der Luftqualität im Klassenzimmer - https://www.geogebra.org/classic/sd7cj7x4
https://www.geogebra.org/classic/sd7cj7x4
- Falls
 und
und  und
und  :
:



- Falls
 und
und  und
und  :
:



- Falls
 und
und  und
und  :
:



- Falls
 und
und  und
und  :
:



- Falls
 und
und  und
und  :
:



- Gesamtlüftungsgütefunktion
 :
:
![{\displaystyle n:[0,9]\times [0,7]\to \mathbb {R} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bf3fbd5ef33e239ed2d7fcabce9ce22e322ac45)

Funktion n in Maxima
(%i33)n(p_1,p_2):=if(LF_2(p_1,p_2)[2]>7 and LF_3(p_1,p_2)[2]≤7 and LF_4(p_1,p_2)[2]≤7)then(i(p_1,p_2))
else if(LF_2(p_1,p_2)[2]>7 and LF_3(p_1,p_2)[2]>7 and LF_4(p_1,p_2)[2]≤7)then(j(p_1,p_2))
else if(LF_2(p_1,p_2)[2]≤7 and LF_3(p_1,p_2)[2]>7 and LF_4(p_1,p_2)[2]≤7)then(k(p_1,p_2))
else if(LF_2(p_1,p_2)[2]>7 and LF_3(p_1,p_2)[2]>7 and LF_4(p_1,p_2)[2]>7)then(l(p_1,p_2))
else(f(p_1,p_2));;
(%o33)n(p₁,p₂):=if [LF₂]₂>7 and [LF₃]₂≤7 and [LF₄]₂≤7) then i(p₁,p₂)
else if [LF₂]₂>7 and [LF₃]₂>7 and [LF₄]₂≤7) then j(p₁,p₂)
else if [LF₂]₂≤7 and [LF₃]₂>7 and [LF₄]₂≤7) then k(p₁,p₂)
else if [LF₂]₂>7 and [LF₃]₂>7 and [LF₄]₂>7) then l(p₁,p₂)
else f(p₁,p₂)
 Plot der Lüftungsgütefunktion n auf der Höhe 1,3
Plot der Lüftungsgütefunktion n auf der Höhe 1,3
- Funktion kann durch Fallunterscheidung in Maxima nicht problemlos integriert oder abgeleitet werden
- Lösung: Funktion
 als Näherung der Lüftungsgütefunktion
als Näherung der Lüftungsgütefunktion
 entspricht Lüftungsgütefunktion, wenn nur das Lotfußpunktverfahren genutzt wird
entspricht Lüftungsgütefunktion, wenn nur das Lotfußpunktverfahren genutzt wird
⇒  ist durch fehlende Fallunterscheidung einfacher zu handhaben
ist durch fehlende Fallunterscheidung einfacher zu handhaben
- Unterschied zwischen
 und
und  ist sehr gering:
ist sehr gering:
 und
und

⇒ Für die Praxis vernachlässigbar
 Vergleich der Funktionen f und n (n ist die untere Funktion, f ist die obere Funktion)
Vergleich der Funktionen f und n (n ist die untere Funktion, f ist die obere Funktion)
- sinnvolle Unterschranke
- theoretisch frei wählbar
- Idee: Mittelwert als untere Schranke
- Weg: Integral geteilt durch Grundfläche des Raumes
- Satz von Fubini, dann Riemann-Integral
- zuerst nach
 über
über ![{\displaystyle [0,9]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/363608267ac9a1e7499c838386bbc69779637cd8) integrieren, dann nach
integrieren, dann nach  über
über ![{\displaystyle [0,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/115bc7b84f1f514c82f3b10d4865f9afaeabed33)

- dann

Berechnung des Integrals der Luftgüte-Funktion mit Maxima
[Bearbeiten]
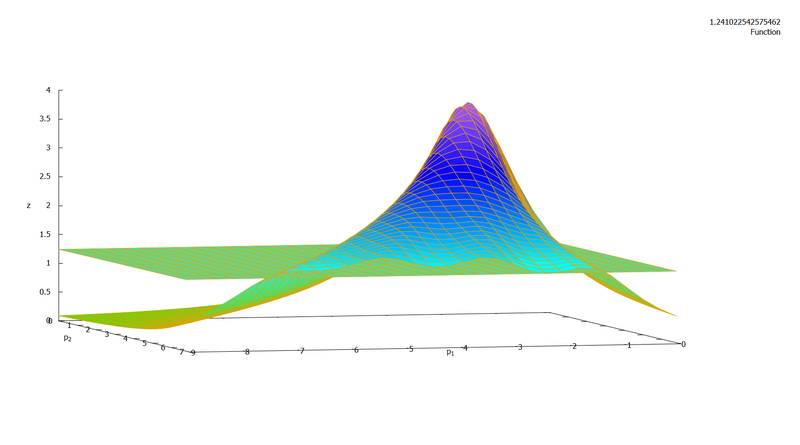 Plot der Luftgüte-Funktion bei fester Raumhöhe 1,3 und mit Mittelwert als Referenzwert
Plot der Luftgüte-Funktion bei fester Raumhöhe 1,3 und mit Mittelwert als Referenzwert
Wie positioniere ich die Schüler? - Gradientenaufstiegsverfahren
[Bearbeiten]- mathematische Methode in mehrdimensionalen Räumen
- Schritte:
- 1. Bestimmung des Gradienten von einem Punkt

- 2. Normierung des Gradienten
- 3. Addition des normierten Gradienten zu
 ergibt
ergibt 
- 4. Funktionswert von
 sollte größer sein, als Funktionswert von
sollte größer sein, als Funktionswert von  , falls nicht: Schrittweite verringern
, falls nicht: Schrittweite verringern
Gradientenaufstiegsverfahren am Beispiel (I)
[Bearbeiten]- In unserem Beispiel: Funktion
 des Typs
des Typs ![{\displaystyle f(p_{1},p_{2})\colon \ [0,9]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/597a72f5fd31b56b53eca7d8a93f4a08bb6f9ea7) x
x![{\displaystyle [0,7]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/32eb15f31667960fad3da7946c711cf4223312db)
- Bestimmung des Gradienten von einem Punkt
 :
:
- Gradient zeigt in Richtung des steilsten Anstiegs am Punkt

- Normierung des Gradienten:

- Addition des normierten Gradienten zu
 ergibt neuen Punkt
ergibt neuen Punkt  :
:

Gradienten Bestimmung durch Maxima Teil 1
[Bearbeiten]
Gradienten Bestimmung durch Maxima Teil 2
[Bearbeiten]![{\displaystyle {\begin{aligned}&{\mathtt {{\color {brown}g}({\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2}):=[{\color {brown}g{\underline {\ }}1}({\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2}),{\color {brown}g{\underline {\ }}2}({\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2})];}}\\&g(p_{1},p_{2}):=[g_{1}(p_{1},p_{2}),g_{2}(p_{1},p_{2})]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/882b811d168277aa40b7e9cb42cbcb01b6d2d9a5)
Gradientenaufstiegsverfahren durch Maxima
[Bearbeiten]x: 9;
9
y: 5;
5
S: [x,y];
[9,5]
if(f(S[1],S[2])<I_2)
then(S: float((g(S[1],S[2] ·1/(sqrt(g(S[1],S[2]).g(S[1],S[2]))))+[S[1],S[2]]))
else(print("Punkt erreicht"), print(S));
Punkt erreicht
[6.58013094730602,6.772900652427504]
[6.58013094730602,6.772900652427504]
Gradientenaufstiegsverfahren am Beispiel (II)
[Bearbeiten]- Funktionswert von
 sollte größer sein, als der Funktionswert von
sollte größer sein, als der Funktionswert von 
- Falls nicht: Schrittlänge verringern (um z. B.
 ):
):

- Der/die Schüler/in am Punkt
 , soll verschoben werden, sodass der Funktionswert
, soll verschoben werden, sodass der Funktionswert  größer als mittlere Lüftungsgüte
größer als mittlere Lüftungsgüte  ist
ist
- Hierzu: Gradientenaufstiegsverfahren hintereinander ausführen, bis neue Position
 des/der Schülers/in über durchschnittlichen Lüftungsgüte liegt
des/der Schülers/in über durchschnittlichen Lüftungsgüte liegt
- Zweiter Schüler darf nicht in die Nähe vom ersten Schüler
- Idee: Luftgüte besetzter Plätze runtersetzen
- Wie? Subtraktion eines Terms, der "Delle" in der Funktion schafft
 Einfluss verschiedener Parameter auf die Glockenkurve - https://www.geogebra.org/classic/rkx4q6e6
Einfluss verschiedener Parameter auf die Glockenkurve - https://www.geogebra.org/classic/rkx4q6e6
[1]
- Addition mit:
![{\displaystyle {{(I_{2}-f(S[1],S[2])-0.5)} \over {(1+{{(p_{1}-S[1])^{2}+(p_{2}-S[2])^{2}} \over {0.5^{2}}}})}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db5947d46f07cc353dafea295bac70acadf1461d)
![{\displaystyle S[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dd5ef70e111a6335a0acd3d05d63266596b66d7) beschreibt erste Komponente von
beschreibt erste Komponente von 
- durch Zähler liegt man am Punkt
 0,5 unter
0,5 unter 
- Nenner
 hat Einfluss auf die Breite der Kuhle (Sicherheitsabstand)
hat Einfluss auf die Breite der Kuhle (Sicherheitsabstand)
![{\displaystyle f_{2}(p_{1},p_{2})=f(p_{1},p_{2})+{{(I_{2}-f(S[1],S[2])-0.5)} \over {(1+{{(p_{1}-S[1])^{2}+(p_{2}-S[2])^{2}} \over {0.5^{2}}}})}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59a8615a80c54604473237d40f7177011e5b66a4)
- Im Folgenden für
 geplottet
geplottet
 Plot der Luftgüte-Funktion bei fester Raumhöhe von 1,3m und Schüler auf (2/1)
Plot der Luftgüte-Funktion bei fester Raumhöhe von 1,3m und Schüler auf (2/1)
- Stärkere Aussagekraft und größere praktische Anwendungsmöglichkeit
- ⇒ Verbesserung gegenüber den ersten beiden Zyklen
- Sitzordnung für jeden Klassenraum bestimmbar
- Abstandsregelung wird berücksichtigt
- auf verschiedene Gegebenheiten anpassbar
- Modell basiert auf Zyklus zwei
- ⇒ Optimierungsmöglichkeiten dieses Zyklus bleiben bestehen
- ⇒ Anpassung der Schrittweite
- Modellierung basiert rein auf Modellannahmen
- ⇒ Datenerhebung zur Kontrolle
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Mathematische Modellbildung' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.






























![{\displaystyle n:[0,9]\times [0,7]\to \mathbb {R} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bf3fbd5ef33e239ed2d7fcabce9ce22e322ac45)





![{\displaystyle [0,9]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/363608267ac9a1e7499c838386bbc69779637cd8)

![{\displaystyle [0,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/115bc7b84f1f514c82f3b10d4865f9afaeabed33)





![{\displaystyle f(p_{1},p_{2})\colon \ [0,9]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/597a72f5fd31b56b53eca7d8a93f4a08bb6f9ea7)
![{\displaystyle [0,7]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/32eb15f31667960fad3da7946c711cf4223312db)





![{\displaystyle {\begin{aligned}&{\mathtt {{\color {brown}g}({\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2}):=[{\color {brown}g{\underline {\ }}1}({\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2}),{\color {brown}g{\underline {\ }}2}({\color {green}p{\underline {\ }}1},{\color {green}p{\underline {\ }}2})];}}\\&g(p_{1},p_{2}):=[g_{1}(p_{1},p_{2}),g_{2}(p_{1},p_{2})]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/882b811d168277aa40b7e9cb42cbcb01b6d2d9a5)






![{\displaystyle {{(I_{2}-f(S[1],S[2])-0.5)} \over {(1+{{(p_{1}-S[1])^{2}+(p_{2}-S[2])^{2}} \over {0.5^{2}}}})}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db5947d46f07cc353dafea295bac70acadf1461d)
![{\displaystyle S[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dd5ef70e111a6335a0acd3d05d63266596b66d7)


![{\displaystyle f_{2}(p_{1},p_{2})=f(p_{1},p_{2})+{{(I_{2}-f(S[1],S[2])-0.5)} \over {(1+{{(p_{1}-S[1])^{2}+(p_{2}-S[2])^{2}} \over {0.5^{2}}}})}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59a8615a80c54604473237d40f7177011e5b66a4)
