Kurs:Mathematische Modellbildung/Themen/Radioaktivität und Risikoliteralität
Modellierungsproblem
[Bearbeiten]Ziel der Modellierung
[Bearbeiten]
Im Zuge des Kohleaustiegs und der Dekarbonisierung wird über die Nutzung von Kernkraftwerken und deren Stellung als möglicherweise nachhaltige und verhältnismäßig CO2-arme Energiequelle weltweit diskutiert. Allerdings bringt Kernkraft unterschiedliche Risiken mit sich. Die verschiedenen Modellierungszyklen verfolgen gemeinsam das Ziel, das Risikobewusstsein für die Gefahren radioaktiver Strahlung zu erhöhen. Der erste Modellierungszyklus fokussiert sich dabei auf den Zeitaspekt. Der zweite Modellierungszyklus bezieht sich dagegen vor allem auf die räumliche Gefahr, die von Atomkraftwerken ausgeht. Der letzte Modellierungszyklus verbindet schließlich den zeitlichen und den räumlichen Aspekt. Somit sollen Schülerinnen und Schüler bzw. Bürgerinnen und Bürger aufgeklärt werden um Risiken und Nutzen von Kernenergie in Verhältnis zueinander setzen zu können.
Zielgruppe der Modellbildung
[Bearbeiten]Niveau der Sekundarstufe I
[Bearbeiten]- Schüler- und Schülerinnen
Die letzten Jahre haben eindrücklich bewiesen, dass insbesondere die jüngeren Generationen auf ein Umdenken in der Klimapolitik drängt. Als besonders wichtiges Anliegen hat sich dabei der Kohleausstieg herauskristallisiert. Bei der Diskussion hinsichtlich alternativer Energiequellen, wie beispielsweise erneuerbaren Energien, müssen allerdings Vor- und Nachtteile diskutiert werden.
Niveau der Sekundarstufe II und Universität
[Bearbeiten]- Wahlberechtigte Bürgerinnen und Bürger
Parteien unterscheiden sich stark in ihrer Herangehensweise zur Begrenzung der Globalen Erwärmung. Gerade der Ausbau alternativer Energiequellen stellt dabei ein Diskussionspunkt dar, mit dem sich wahlberechtigte Bürgerinnen und Bürger vor Stimmabgabe auseinander setzen sollten.
- Politik (Einhaltung der Klimaschutzziele)
Die Politik hat sich in dem Pariser Klimaabkommen verpflichtet, die Erhöhung der weltweiten Durchschnittstemperatur auf 1,5 Grad Celsius zu begrenzen. Somit müssen sich auch Politikerinnen und Politiker über zukunftsrealistische Energiequellen beraten.
- Industrie und Verbraucher
Die Industrie ist in den allermeisten Fällen direkt abhängig von Energie und elektrischem Strom. Somit unterliegt der industrielle Sektor direkten Konsequenzen von Änderungen in der Energiewirtschaft.
Mehrwert der Modellbildung
[Bearbeiten]- Schutz/ Erhalt natürlicher Lebensgrundlagen
In den Modellbildungszyklen sollen die Gefahren durch die Nutzung radioaktiver Energieerzeugung aufgezeigt werden. Bei einer Kernschmelze würde nämlich eine große Fläche für Jahrzehnte oder gar Jahrhunderte unbewohnbar und verseucht sein. Dies ist etwa in der Sperrzone von Tschernobyl erkennbar.
- Sicherung von Wohlstand
Der Energiesektor muss sich in Zeiten der Dekarbonisierung massiv wandeln. Dennoch sollte der Wohlstand in Deutschland möglichst hoch bleiben. Kernenergie bietet aufgrund des geringen CO2-Ausstoßes bei niedrigen Kosten zur Stromherstellung vielversprechende Möglichkeiten dazu. Durch die Modellbildung werden die Risiken von Kernenergie modelliert. Daher wird die Faktenlage bei einer Entscheidung für oder gegen Kernkraftwerke verbessert.
- Planung möglicher Atomkraftwerke
Der zweite und dritte Modellbildungszyklus könnte auch dazu genutzt werden, potentielle Standorte von Atomkraftwerken auszuwählen. Mit Blick auf die Hauptwindrichtung können Sie nämlich dort gebaut werden, wo in Hauptwindrichtung keine größeren Städte liegen.
- Sensibilisierung von Schülerinnen und Schülern
Radioaktivität ist eine nicht sichtbare Gefahr. Die Modellbildung hilft dabei, zu verstehen, wie lange eine radioaktive Verschmutzung andauern kann und welche räumlichen Gebiete bei einer Kernschmelze betroffen wären.
Zuordnung zu Nachhaltigkeitszielen
[Bearbeiten]- Radioaktive Strahlung in größeren Dosen schränkt die Gesundheit ein. Um bestmögliche Gesundheit garantieren zu können, muss man sich mit den Risiken von Kernenergie auseinandersetzen.
- Die Folgen des Klimawandels sind schon heute global spürbar. Aus diesem Grund ist das Ziel bis zum Jahr 2030 hauptsächlich auf saubere und erneuerbare Energien zu setzen. Um dieses Ziel realistisch verfolgen zu können, muss ein Wechsel und Umdenken hinsichtlich der Energieversorgung stattfinden.
- Die fortschreitende Digitalisierung und die aufkommende E-Mobilität sind unter anderem Gründe für einen steigenden Strombedarf. Emissionsfreie Energiearten sind hierbei ein wichtiger Faktor, um diesen Strombedarf zu decken und gleichzeitig das Klima erhalten zu können.
Modellierungszyklen
[Bearbeiten]Modellierungszyklus
[Bearbeiten]
In dem Modellierungszyklus wird nach dem Finden des Problems in mehreren Schritten:
- das Problem idealisiert und mathematisiert
- mathematisch bearbeitet, sodass sich mathematische Lösungen ergeben
- bewertet
- optimiert
Modellierungszyklus 1 - Niveau Sekundarstufe 1
[Bearbeiten]Die Modellierung des ersten Modellierungszyklus fokussiert die Umsetzung mit Schülerinnen und Schüler. Die Schülerinnen und Schüler sollen aktiv erste Erfahrungen für den Prozess eines radioaktiven Zerfalls erhalten, indem sie ein Zufallsexperiment selbst durchführen.
- Modellierung des exponentiellen Zerfalls von radioaktiven Stoffen
- Veranschaulichung der zeitlichen Spanne, die Zerfallsprozesse einnehmen können
Ziel
[Bearbeiten]- Bewusstsein für Radioaktivität schaffen
- Zufallsgesteuerten Prozess sichtbar machen ⇒ ergibt e-Funktion
Inhaltliche Beschreibung
[Bearbeiten]- Betrachtung einer großen Anzahl radioaktiver Nuklide, die mit einer gewissen Wahrscheinlichkeit zerfallen
- Feste Zeitintervalle mit einer jeweils konstanten Zerfallswahrscheinlichkeit
- Plotten der Anzahl zerfallener Nuklide in Abhängigkeit von der Zeit
- Vergleich mit einer realen Zerfallskurve (durch Halbwertszeit und Anfangsanzahl)
Mithilfe eines Zufallsexperiment in Form eines Würfelmodells können Schülerinnen und Schüler der Sekundarstufe I erste Erfahrungen mit Radioaktivität und radioaktivem Zerfall sammeln. Dabei ist vorwegzunehmen, dass dieser Würfelversuch für die entsprechende Schülergruppe didaktisch sehr reduziert ist und wichtige Aspekte eines realen radioaktiven Zerfalls vernachlässigt, auf die in der Bewertung der Modellierung eingegangen werden soll.
Benötigt für den Versuch wird lediglich eine vorgegebene Anzahl von Würfeln. Dabei entspricht die Anzahl der Würfel der Anzahl der radioaktiven Teilchen. Jeder Wurf entspricht einer gewissen Zeiteinheit (z.B. für Jahre oder Jahrzehnte). Zu Beginn des Versuchs werden alle Würfel gewürfelt. Daraufhin werden diejenigen Würfel, die eine festgelegte Augenzahl besitzen, beispielsweise die Augenzahl 6, entfernt. Anschließend ist die Anzahl der verbleibenden Würfel sowie der zu entfernenden Würfel zu bestimmen und in einer Tabelle zu dokumentieren. Die zu entfernenden Würfel entsprechen dabei den zerfallenen Teilchen und die verbleibenden Würfel entsprechend den noch vorhandenen radioaktiven Teilchen. In diesem Fall entspricht die Wahrscheinlichkeit für den Zerfall eines radioaktiven Teilchens , wobei die Annahme getroffen wird, dass die Zerfallsreihe des Teilchens nach diesem ersten Zerfall endet. Dementsprechend wird ebenfalls angenommen, dass keine Zerfallsprodukte entstehen. Der Würfelversuch endet sobald alle Würfel entfernt wurden und somit keine radioaktiven Teilchen mehr vorhanden sind.
Mathematisches Modell
[Bearbeiten]Der Würfelversuch als Laplace Experiment kann mithilfe einfacher Stochastik beschrieben werden. Die Ergebnismenge des Zufallsexperiment entspricht der Menge . Die Wahrscheinlichkeit für das Ereignis eine festgelegte Augenzahl, hier die Augenzahl 6, zu würfeln entspricht . Die Wahrscheinlichkeit für das Ereignis diese Augenzahl nicht zu würfeln entspricht . Führt man das Zufallsexperiment n-mal unabhängig voneinander, unter identischen Bedingungen durch, lassen sich die absoluten und relativen Häufigkeiten, bei denen das jeweilige Ereignis eingetreten ist bestimmen. Führt man das Zufallsexperiment wiederholt durch, so stabilisiert sich die relative Häufigkeit des Ereignisses mit wachsender Versuchszahl n (Gesetz der großen Zahlen).
Die Anzahl der verbleibenden Würfel nach dem ersten Wurf berechnet sich durch die Anzahl der Würfel multipliziert mit der Wahrscheinlichkeit, dass die Augenzahl 6 nicht fällt. Dieses Vorgehen zur Bestimmung der verbleibenden Würfel kann man nach jedem Wurf durchführen. Für die Anzahl der verbleibenden Würfel nach dem n-ten Wurf ergibt sich demnach für Würfel zu Beginn insgesamt: .
Exponentielle Abnahmen beschreiben Vorgänge, bei denen sich Größen exponentiell ändern. Die Gleichung beschreibt also die Abnahme einer Größe A innerhalb einer bestimmten Zeitspanne . gibt dabei den Wert der Größe zu Beginn an. Überträgt man dies auf den radioaktiven Zerfall nimmt die Kernanzahl mit zunehmender Zeit ab und geht langsam gegen Null.
Software
[Bearbeiten]Das Zufallsexperiment wird mit dem Tabellenkalkulationsprogramm Libre Office modelliert. Dazu wird für jedes betrachtete Startatom (in dieser Modellierung 50 Stück) eine eigene Zeile erstellt. In der ersten Spalte steht die dazugehörige Nummer eines jeden Atoms; letztlich werden also die Zahlen von 1 bis 50 untereinander aufgelistet. In der Spalte daneben wird der Zustand - also zerfallen oder noch vorhanden - durch die Zahlen 1 und 0 codiert. Dabei steht in dem gesamten Dokument die Zahl 1 für ein zerfallenes Atom und die Zahl 0 für ein Atom, welches noch vorhanden ist.

Die Modellierung wird im folgenden exemplarisch für das erste Atom respektive die erste Zeile der Tabellenkalkulation dargelegt. Die Zuweisung erfolgt durch die Auswertung einer Zufallszahl. Über den Befehl
WENN(ZUFALLSBEREICH(1;$C$1)=6;1;0)
wird eine Zufallszahl im Bereich von 1 bis zu einer festgelegten Obergrenze in der Zelle C1 ausgewertet. Im Falle der Modellierung mit Hilfe eines Würfels würde gelten C1=6. Ist diese Zufallszahl gleich 6, so zerfällt das Atom. Anderenfalls wird die Zahl 0 zugeordnet - das Atom existiert weiter. Dies ist die Modellierung des ersten Würfelvorgangs.
In der nächsten Spalte werden alle noch vorhandenen Atome unverändert durch ihre Startnummer (Zeilennummer) repräsentiert. Den zerfallenen Atomen wird durch die Abfrage
WENN(B3=0;A3;"Zerfallen")
der Ausdruck "Zerfallen" zugeordnet und durch eine bedingte Formatierung rot hinterlegt. Den noch vorhandenen Atomen wird ihre Nummer aus der ersten Spalte zugeordnet und sie werden durch eine bedingte Formatierung grün hinterlegt.
Nun erfolgt die Modellierung des nächsten Zeitschritts mit entsprechenden Zerfällen. Dazu wird folgender Befehl genutzt:
WENN(ODER(ZUFALLSBEREICH(1;$C$1)=6;C3="Zerfallen");1;0)
Auch hier werden die Zahlen 0, stellvertretend für noch vorhandene Atome und 1 für zerfallene Atome zugeordnet. Ein Atom gilt dabei als zerfallen, falls das Atom im vorangegangenen Schritt bereits zerfallen ist (weshalb der Ausdruck "Zerfallen" zugeordnet wurde) oder eine zufällige Zahl gleich 6 ist und somit ein noch vorhandenes Atom zerfällt. Nun wird wieder abgefragt, welchen Atomen der Wert 1 zugeordnet wurde, um diesen letztlich den Ausdruck "Zerfallen" rot unterlegt zuzuordnen, sodass sie ab diesem Zeitpunkt als zerfallen gelten. Dazu wird wieder der Befehl
WENN(D3=0;C3;"Zerfallen")
verwendet.
Folgend können alle weiteren Zeitpunkte durch die letzten beiden Schritte mit den Befehlen
WENN(ODER(ZUFALLSBEREICH(1;$C$1)=6;C3="Zerfallen");1;0)
und
WENN(D3=0;C3;"Zerfallen")
modelliert werden, wobei die Zellen entsprechend angepasst werden müssen.
Die Anzahl der vorhandenen Atome kann zu jedem Zeitpunkt durch den Befehl
ZÄHLENWENN(B3:B52;0)
(hier exemplarisch für die Anzahl der vorhandenen Atome nach dem ersten Zeitschritt) ermittelt werden, da hier in allen Zeilen einer Spalte die Anzahl der zugeordneten Nullen gezählt wird, die gerade den noch vorhandenen Atomen entspricht.
Diese Simulation des Würfelexperimentes kann prinzipiell für eine beliebige Anzahl an Startatomen, beliebige Zufallswahrscheinlichkeiten und für beliebig viele Zeitschritte erstellt werden. Da das simultane Generieren und Abfragen von Zufallszahlen in vielen Zellen gleichzeitig aber eine große Rechenleistung erfordert, kann es für eine große Anzahl an Startatomen sowie Zeitpunkten zu Programmabstürzen kommen.
Resultate der Modellierung
[Bearbeiten]Die über den Befehl ZÄHLEWENN noch vorhandenen Atomkerne werden zur besseren Übersicht unterhalb der Modellierung in einer Tabelle dargestellt. Demnach erhält man beispielsweise folgende Werte:

Wandelt man diese Rohwerte in eine Graphik um, so erhält man folgende Anschauung:

Man erkennt die exponentielle Abnahme in der rechten Graphik durch die Krümmung bzw. in der linken Graphik nach Logarithmieren durch den näherungsweise linearen Verlauf. Weitergehend wäre ebenfalls eine Durchführung einer linearen Regression möglich.
Resultate in Realsituation
[Bearbeiten]Physikalische Erklärung
[Bearbeiten]Eine Probe eines radioaktiven Isotops besteht aus einer großen Menge radioaktiver Kerne. Diese Kerne zerfallen nicht alle gleichzeitig, sondern innerhalb eines gewissen Zeitintervalls. Es handelt sich dabei um einen Zufallsprozess. Allerdings entspricht die Wahrscheinlichkeit, dass ein radioaktives Teilchen zerfällt nicht der Wahrscheinlichkeit, dass eine bestimmte Augenzahl beim Würfeln fällt. Weiterhin ist eine genaue Vorhersage wann ein bestimmter Kern zerfällt nicht möglich, sondern nur eine ungefähre Abschätzung auf Grundlage von Wahrscheinlichkeiten. Unter der Annahme, dass jeder Kern in jedem Moment seiner Existenz die gleiche Zerfallswahrscheinlichkeit besitzt, ist eine Aussage darüber möglich, wie viele Kerne in einer Probe in einem gegebenen Zeitintervall zerfallen.[1]
Die Anzahl der in einem sehr kurzen Zeitintervall stattfindenden Zerfälle ist proportional zu und der der Gesamtzahl der vorhandenen radioaktiven Kerne:
entspricht dabei der Zerfallskonstante, die je nach Nuklid unterschiedliche Werte annimmt. Je größer der Wert für ist desto größer ist entsprechend die Zerfallsrate und desto radioaktiver ist das Isotop bei einer vorgegebenen Anzahl von Kernen. bezeichnet die Anzahl der in dem Zeitintervall stattfindenden Zerfälle.[1]
Schreibt man die obige Formel in infinitesimaler Form lässt sich durch entsprechende Integration das radioaktive Zerfallsgesetz herleiten. Dabei ergibt sich die Integrationskonstante , welche der Anzahl der zur Zeit vorhandenen Mutterkerne entspricht. entspricht der Anzahl der zur Zeit verbliebenen Kerne.
Das radioaktive Zerfallsgesetz besagt, dass die Anzahl der radioaktiven Kerne in einer gegebenen Probe mit der Zeit exponentiell abfällt. Somit wird die Beschreibung eines radioaktiven Zerfalls mithilfe der Exponentialfunktion vorgenommen. Die Modellierung entspricht insofern der Realität, dass Sie die exponentielle Abnahme radioaktiver Nuklide widerspiegelt. [1]
Für den radioaktiven Zerfall respektive die Zerfallsrate eines Isotops wird anstatt der Angabe der Zerfallskonstanten häufig eher der Begriff der Halbwertszeit verwendet. Die Halbwertszeit eines Isotops ist definiert als die Zeit, nach der sich die Menge eines Isotops in einer Probe halbiert hat. Dieses Verhalten wird durch die Exponentialfunktion charakterisiert. Je größer die Halbwertszeit eines Isotops desto langsamer zerfällt es ( wird kleiner - Inverse Beziehung von Halbwertszeit und Zerfallskonstanten) . [1]
Die Halbwertszeit radioaktiver Isotope variiert. Beispielsweise hat Uran-235 eine Halbwertszeit von Jahren. Radon allerdings, welches beim Zerfall von Uran-238 entsteht und über die Hälfte der natürlichen Strahlenbelastung ausmacht, hat lediglich eine Halbwertszeit 3,82 Tagen. In Bezug auf die Modellierung im Sinne des Würfelversuch, kann die Halbwertszeit, also die Zeit nach der noch die Hälfte der ursprünglichen Anzahl radioaktiver Teilchen vorhanden ist, aus den erhobenen Daten ermittelt werden. Die Zerfallskonstante lässt ebenfalls sich aus dem Graphen (nicht logarithmiert) ermitteln.
Da die Zerfallsrate proportional zu ist, verringert sie sich bei jeder Halbwertszeit um einen Faktor zwei. Mit bei ergibt sich dadurch: beziehungsweise . Durch logarithmieren ergibt sich für die Halbwertszeit . Insgesamt ergibt sich damit für die Funktion zur mathematischen Beschreibung des radioaktiven Zerfalls . [1]


Zerfall von Cs-137
[Bearbeiten]In Nuklearkatastrophe von Tschernobyl wird dargestellt, dass Cs-137 noch heute das am stärksten strahlende Nuklid ist[2]. Um die Gefahren radioaktiver Abfälle abschätzen zu können, ist es daher sinnvoll, im Zuge der Modellierung Cs-137 zu thematisieren. Dessen Halbwertszeit liegt bei ca. 30 Jahren und es entsteht nicht natürlich. In Hinblick auf unsere Modellierung mit 50 Startatomen und einer Halbwertszeit von ca. vier Zeiteinheiten wären selbst nach 4 Halbwertszeiten (entspricht 120 Jahren) noch fünf Atome von Cs-137 übrig. Damit lässt sich erahnen, dass Atommüll jahrzehntelang sehr gefährlich bleibt und einen starken Eingriff in die Natur darstellt.
Atommüll weist zudem sehr viele, zum Teil Millionen Jahre lang strahlende Nuklidanteile auf (Halbwertszeit von Iod-129: a), sodass für diese lange Zeitspanne sichergestellt werden muss, dass er nicht in die Atmosphäre oder in den Grundwasserspeicher gelangt. Andernfalls kann eine lange Auseinandersetzung zu starken Genmutationen und damit zu Krebs führen.
Bewertung & Optimierung
[Bearbeiten]Bei dieser Modellierung wurde angenommen, dass die Teilchen nach dem Zerfallen tatsächlich nicht mehr vorhanden sind, bzw. für unsere Anschauung nicht mehr relevant sind. In der Realität treten allerdings sogenannte Zerfallsketten auf. So können sich einige Atomkerne mehr als acht mal durch Zerfallsprozesse umwandeln, bis ein stabiler Atomkern entsteht, der nicht weiter zerfällt. Auch eine reine Betrachtung von Cs-137 stellvertretend für alle Nuklide in Atommüll ist eine starke Vereinfachung. Cs-137 macht nur einen Teil der Spaltprodukte (diese wiederum nur 4% des radioaktiven Abfalls) in Atommüll aus. So existieren in den ersten Jahren sehr viele hochradioaktive Stoffe, die deutlich mehr Strahlung abgeben, jedoch schnell zerfallen. Außerdem enthält Atommüll schwach radioaktive Stoffe, die unnatürlich entstanden sind und noch für tausende von Jahren radioaktiv strahlen. Eine Gesamtmodellierung all dessen würde das Schulniveau jedoch vollkommen übersteigen und wäre mit hohem Programmierungsaufwand und vielen bedingten Wahrscheinlichkeiten verbunden, die den Rahmen des Seminars sprengen würden und darüber hinaus nur wenige zusätzliche Erkenntnisse liefern würde. Die exponentielle Abnahme bleibt nämlich strukturgleich.
In diesem Modellierungsprozess wurden lediglich 50 Nuklide betrachtet. In einem Atomkraftwerk ist eine bedeutend höhere Anzahl an Teilchen vertreten: Bei einem einzigen Kilogramm Caesium liegt die Atomanzahl im Bereich von . Diese Größenordnung lässt andeuten, dass die Abschätzung mit 50 Atomen viel zu klein gegriffen ist. Die Berechnung von 50 Nukliden führte in LibreOffice Calc jedoch bereits zu einigen Abstürzen. Um bedeutend größere Anzahlen zu berechnen, müsste man wohl Statistik-Programme verwenden. Aufgrund der leichten Zugänglichkeit und Vertrautheit für SuS haben wir uns jedoch für eine Modellierung mit Hilfe von Tabellenkalkulation entschieden.
Neben der zeitlichen Komponente des Risikos von Radioaktivität spielt auch die örtliche Komponente eine besondere Rolle. Als Beispiel lässt sich hier die Reaktorkatastrophe in Fukushima nennen: Nach der Ausschüttung radioaktiven Materials gelang dieses in die Luft und in die Wolken. Aufgrund der in Japan vorherrschenden Westwinde wurden diese Wolken über den Pazifik getrieben. Daher hatten, trotz der wesentlich größerer Entfernung, selbst weit entfernte Gebiete über dem Pazifik wesentlich höhere radioaktive Belastungen als beispielsweise das nahegelegene Korea, welches östlich von Fukushima liegt (siehe Aoyama (2018) Abbildung 13 [3]). Um diesen Faktor entsprechend berücksichtigen zu können, wird im nächsten Modellierungsprozess eine solche örtliche Abhängigkeit betrachtet.
Modellierungszyklus 2 - Niveau Sekundarstufe 2
[Bearbeiten]- Modellierung einer möglichen Verteilung von radioaktivem Material im Raum im Anschluss an eine Reaktorkatastrophe
- Relevanz von Windrichtung in Bezug auf den radioaktiven Fallout
- Verknüpfung zur radioaktiv belasteten Wolke nach dem Reaktorunglück in Tschernobyl, weswegen hauptsächlich der westliche und nördliche Bereich Europas von der Katastrophe betroffen waren und sind.
Ziel
[Bearbeiten]- Bewusstsein für Radioaktivität schaffen
- Erkenntnisse zu räumlicher Ausdehnung und Verbreitung von radioaktivem Material
Inhaltliche Beschreibung
[Bearbeiten]Die Modellierung realisiert die Flugbahn einer radioaktiven Wolke und den anschließenden radioaktiven Niederschlag nach einer Kernreaktorkatastrophe. Idealisiert wird nur die Flugbahn einer einzigen radioaktive Wolke betrachtet.
Um diese zu modellieren müssen zuvor einige Annahmen getroffen werden:
1. Die Starthöhe der radioaktive Wolke befindet sich in Höhe.
2. Die Windgeschwindigkeit ist konstant und soll betragen.
3. Die radioaktive Wolke wird vereinfacht als ein Punkt modelliert.
4. Bis zum Abregnen befindet sich die radioaktive Wolke konstant auf der gewählten Starthöhe von .
5. Die Fallgeschwindigkeit des Regens wird als konstant auf festgelegt.
6. Da die radioaktive Wolke als ein Punkt modelliert wurde, muss die weitere Annahme und Vereinfachung vorgenommen werden, dass der Regen ebenfalls in einem einzigen Punkt auftrifft.
Der Startpunkt der Modellierung befindet sich in Philippsburg. Hintergrund dessen ist das seit Jahresbeginn 2020 stillgelegte Kernkraftwerk in Philippsburg im Landkreis Karlsruhe, Baden-Württemberg. Die Entfernung Philippsburg von Landau entspricht lediglich . Somit eignet sich der Start in Philippsburg sehr gut, um den Schülerinnen und Schüler der Landauer Schulen die Relevanz der Modellierung aufzuzeigen. Dahingehend könnte weiter thematisiert werden in wie weit Landau von einer Reaktorkatastrophe in Philippsburg betroffen wäre.
Die radioaktive Wolke startet demnach im Punkt in Höhe über Philippsburg. Durch den Wind mit konstant angenommener Windgeschwindigkeit und variabler Windrichtung wird die Wolke in einer bestimmten Zeiteinheit und in weiterhin Höhe weggetragen. Der Punkt, indem sich die Wolke zum Zeitpunkt befindet, wird durch den Punkt verdeutlicht. Die Zeit ist dabei variabel und in Stunden angegeben. Ab dem Zeitpunkt beginnt das Abregnen der radioaktiven Wolke und der Regen fällt mit der Fallgeschwindigkeit zu Boden. Die Zeit ist ebenfalls variabel und in Stunden angegeben. Der Auftreffpunkt des Regens wird durch den Punkt verdeutlicht.
Mathematisches Modell & Computergestützte Umsetzung
[Bearbeiten]Grundlage der Modellierung bildet die Vektorrechnung bzw. Analytische Geometrie der Sekundarstufe II. Die Modellierung wird realisiert durch verschiedene Punkte und Linearkombinationen im dreidimensionalen reellen Vektorraum. Dahingehend wird das Rechnen mit Vektoren vorausgesetzt.
Ausgehend von einem gewählten Startpunkt im Dreidimensionalen wird unter Berücksichtigung der Windrichtung sowie der Windgeschwindigkeit eine Bahnkurve aufgestellt, entlang der sich die modellierte radioaktive Wolke bewegt. Die Bahnkurve beziehungsweise der Aufenthaltspunkt im Dreidimensionalen der radioaktiven Wolke ergibt sich demnach aus dem Startpunkt im Dreidimensionalen addiert mit dem Produkt aus der Zeit , die seit Beginn der Bewegung vergangen ist und dem Vektor , der die Windrichtung sowie die Windgeschwindigkeit berücksichtigt. Ab dem Zeitpunkt des Abregnens ist eine neue Bahnkurve erforderlich. Diese wird durch den Vektor repräsentiert, welcher sich zusammensetzt aus dem Vektor addiert mit dem Produkt aus der Zeit , die seit Beginn des Abregnens vergangen ist und dem Vektor addiert mit dem Produkt aus der Zeit und dem Vektor , welcher die Fallgeschwindigkeit des Regens repräsentiert.
Die Modellierung der Flugbahn von radioaktivem Material in Wolken wurde über die dynamische Geometrie-Software GeoGebra realisiert. Der Vorteil hierbei liegt in der parallelen und dynamischen Darstellung von Objekten in einem 2-dimensionalen und gleichzeitig in einem 3-dimensionalen Koordinatensystem. Um die Veranschaulichung der Modellierung zu stärken, sowie den Erkenntnisgewinn von Schülerinnen und Schülern durch eine möglichst konkrete Anschauung zu stärken, wird in die 2-dimensionale Ansichtsebene eine Europakarte maßstabsgetreu eingefügt. Der Ursprung liegt dabei genau in Philippsburg. Eine Längeneinheit entspricht in der Modellierung einem Kilometer.



Die Konstruktion beginnt mit dem Erstellen von einem Startpunkt . Da die Wolke in 12 Kilometern Höhe starten soll ist gewählt als Vektor . Für die Ansicht in dem zweidimensionalen Betrachtungsfeld, wird von jedem Punkt ein weiterer Punkt erstellt, der die Projektion auf die x-y-Ebene darstellt. Für den Punkt ergibt sich: .
Für die Windrichtung wird ein erster Richtungsvektor festgelegt, der lediglich die Richtung angibt aber noch keine Windgeschwindigkeit/Windstärke berücksichtigt: . Der Wert von kann dabei im Bereich von über einen Schieberegler variiert werden. Wird zusätzlich die durchschnittliche Windgeschwindigkeit berücksichtigt, so ergibt sich der eigentliche Vektor der Windrichtung durch . Diese Aufspaltung des Windverktors in Betrag und Richtung erlaubt die flexible Variation der Windstärke in der Konstruktion. Um diesen Vektor trotz großer Skalierung visuell wahrnehmen zu können, wird ein zusätzlicher Vektor eingebaut, für den gilt:
Für den verschobenen Startpunkt,ergibt sich ein neuer Punkt , der folgendermaßen kontruiert wird: . Auch hier wird ein projezierter Punkt auf der x-y-Ebene konstruiert. Es gilt:
Die Zeit kann dabei in einem Schieberegler variiert werden. Ab dem Zeitpunkt des Ausregenens wird der Schieberegler von relevant. Der Punkt wird dann zusätzlich über den Vektor , den sognannten Fallvektor, verschoben. Es gilt dann
Resultate der Modellierung
[Bearbeiten]Mithilfe der Modellierung kann man also berechnen, an welchem Ort radioaktiver Niederschlag in Folge einer Kernschmelze zu erwarten ist. In unserer Modellierung betrachten wir stellvertretend ein mögliches Unglück im Kraftwerk Philippsburg (der Ort kann durch in Bewegen der Karte auch angepasst werden). Der Aufrittpunkt des Mittelpunktes des radioaktiven Materials lässt sich dann bestimmen. An dieser Stelle wird dies nun für "typische" Verhältnisse gemacht: aufgrund der geographischen Lage Europas in der Westwindzone wollen wir von Westwind (mit einer Geschwindigkeit von ) ausgehen. Typischerweise regnet es im Schnitt in Europa an jedem dritten Tag. Das heißt man stellt für die Schieberegler folgendes ein:
Mit dem Schieberegler lässt sich dann die Zeit einstellen, bis der Regen zu Boden fällt. Anhand der unteren Abbildung lässt sich dann klar erkennen, das sich der Niederschlag an der slowakisch-ukrainischen Grenze ereignen würde.
Unabhängig von der Windrichtung gibt es auch die Möglichkeit, die Reichweite der Wolke in Abhängigkeit von der Dauer bis zum nächsten Regen zu bestimmen. Dazu kann man sich in Geogebra zum Punkt die Spur anzeigen lassen. Unter den übrigen Annahmen zeigt dann die untenstehende Abbildung den Kreis (als Ansammlung von Punkten), auf dem sich potentiell der Niederschlag ereignen könnte.

Die Modellierung stellt also ein interaktives Tool dar, um das Herabregnen radioaktiver Nuklide in der Atmosphäre räumlich bestimmen zu können.
Resultate in Realsituation
[Bearbeiten]
Die Abhängigkeit zwischen radioaktiver Verschmutzung und Windrichtung wird am Beispiel der Nuklearkatastrophe von Fukushima ersichtlich. Mit Hilfe der rechten Abbildung wird die Kontamination der Umgebung von Fukushima mit radioaktiven Nukliden verdeutlicht. In der Abbildung ist erkennbar, dass die radioaktive Verschmutzung am Boden sehr viel stärker von einer bestimmten Richtung (der Windrichtung) abhängig ist als vom radialen Abstand zum betroffenen Atomreaktorblock.
Neben der Windrichtung ist es entscheidend, wo es zu einem Radioaktivem Niederschlag (dem sogenannten Fallout) kommt. Ein Fallout entsteht etwa dann, wenn nach einem schwerwiegenden Reaktorunfall Staub - meist nach einer Explosion - in die Atmosphäre gelangt. Dieser Staub trägt viele radioaktive Partikel mit sich, die sich als Aerosol verteilen. Dies ist überaus gefährlich, denn "daraus entstehender Niederschlag mit Staub als Kondensationskeim wird auf der Erdoberfläche festgestellt und gemessen. Die Radioaktivität der Staubpartikel bringt eine erhebliche radioaktive Strahlenbelastung und gegebenenfalls Vergiftung (Strahlenkrankheit) mit sich" [4].
Eine Sonderform ist der sogenannte Washout. Bei diesem fallen radioaktive Teilchen von oben auf eine Wolkendecke oder vereinigen sich mit den Regentropfen in der Wolke und fallen zu Boden. Dadurch kann es noch in großen Entfernungen von der Quelle bei auftretenden Niederschlägen zu einer großen Belastung durch kontaminierten Teilchen kommen.
Die eben beschriebenen Effekte tauchen auch sehr deutlich bei der Nuklearkatastrophe von Tschernobyl auf:
Bei der Kernschmelze und der Explosion des Reaktorblocks kam es bauartbedingt zu einem Graphitbrand. Bei diesem gelangten gasförmige oder leicht flüchtige Stoffe wie Jod und Caesium in eine Höhe von 3,5km - 10km[5].
In Folge dessen wurden die Radionuklide in einer ersten Wolke über Polen nach Skandinavien verteilt. Eine zweite Wolke verbreitete die Nuklide über die Slowakei, Tschechien und Österreich nach Deutschland. Die dritte und letzte signifikante Wolke belastete Rumänien, Bulgarien, Griechenland und die Türkei [6].
In Bezug auf Deutschland lagen die Bodenkontaminationen in den am stärksten belasteten Gebieten (Südosten von Bayern) rund zehnmal höher als im Norden.
Bewertung & Optimierung
[Bearbeiten]Die Modellierung der radioaktiven Wolke als Punkt stellt eine nicht zu vernachlässigende Vereinfachung dar. Die Wolke könnte beispielsweise auch als Kugel oder Ellipsoid modelliert werden, dessen Mittelpunkt abhängig von der Variable t ist, welche die zeitliche Bedingtheit widerspiegelt. Ist die Windrichtung konstant, so verfolgt dieser Mittelpunkt eine Gerade im dreidimensionalen Raum. Die radioaktive Wolke, modelliert als Kugel, würde zu Beginn einen kleinen Radius besitzen, der sich mit der Zeit immer weiter vergrößert. Dabei würde die Partikeldichte bei größeren Radien zunehmend geringer werden (Diffusionsprozesse).
Alle getroffenen Annahmen stellen Kritikpunkte der Modellierung dar:
- Starthöhe:
Die Starthöhe wurde als ein fester Punkt angenommen. Jedoch kann die angenommene Starthöhe schwanken und somit zu anderen Werten führen. Außerdem könnten sich unterschiedliche radioaktive Partikel auf unterschiedlichen Höhen befinden. Die Annahme, dass die Gesamtheit sich in einem einzigen Punkt vereinigt, ist eine nicht zu vernachlässigende Näherung.
- Radioaktive Partikel sinken vor dem Abregnen nicht zu Boden:
In unserer Modellierung wird die höhere Dichte der Staubpartikel im Vergleich zur Luft ignoriert. Bis es regnet bewegen sich unsere Partikel lediglich parallel zum Boden. Dadurch wird ein nicht vernachlässigbarer Teil der Verschmutzung nicht berücksichtigt.
- Konstante Windrichtung und Konstante Fallgeschwindigkeit:
In unserer Modellierung ist der Wind sowohl in Betrag als auch in Richtung zeitlich und räumlich konstant. Dies ist eine starke Vereinfachung der komplexen Wetterphänomene. Gleiches gilt für die Fallgeschwindigkeit des Regens.
- Zeitliche Dauer der Freisetzung nicht beachtet:
In unserem Modell wird angenommen, dass sich alle Partikel anfangs bereits in der Luft befinden und keine weiteren freigesetzt werden. Es wird demnach lediglich ein Ausstoß von radioaktivem Material betrachtet. Diese Annahme beschreibt lediglich eine wirkliche Kernexplosion zutreffend.
Ein weiteres Problem stellen geographische Gegebenheiten dar: Wolken ziehen beispielsweise nicht ohne Weiteres über Gebirge, bspw. die Alpen, hinweg. Die allgemeine Modellierung für alle Windrichtungen und Zeit-Einstellungen gibt jedoch eine detailliertere Beschreibung eines konkreten Falles, wie bspw. ein nord-west-Wind, der über die Alpen zieht nicht her. In der Erstellung des Modells musste daher entschieden werden, ob eine Modellierung für alle möglichen Windrichtungen oder für eine bestimmte Windrichtung unter Berücksichtigung der weiteren spezifischen Faktoren erzeugt wird. Da das Ziel der Modellierung ist, die räumliche Verbreitung zu vermitteln und ein Eindruck für die Ausdehnung von radioaktivem Material zu verschaffen, ist die allgemeine Variante anschaulicher, da unterschiedliche Fälle eingestellt werden können. Vorteilhaft bei der Nutzung von GeoGebra stellte sich die gleichzeitige 2-Dimensionale und 3-Dimensionale Modellierung heraus, welche ebenfalls für Schülerinnen und Schüler hilfreich sein könnte, um die Zusammenhänge besser zu verstehen.
Modellierungszyklus 3 - Niveau Uni
[Bearbeiten]Ziel
[Bearbeiten]Ziel dieses letzten Modellierungszyklus ist es, sowohl die zeitliche als auch die räumliche Modellierung zu verbinden und somit die Gefahr einer Kernschmelze in einem Kernkraftwerk umfänglich zu veranschaulichen. Dabei richtet sich der Modellierungszyklus an alle Bürgerinnen und Bürger und soll vor allem der Aufklärung dienen. Die Modellierung kann außerdem genutzt werden, um mit Hilfe von Wetterdaten die qualitative radioaktive Kontamination bei einem Reaktorunglück zeitlich und räumlich abschätzen zu können.
Inhaltliche Beschreibung
[Bearbeiten]Inhaltlich soll eine Funktion modelliert werden, die jedem zweidimensionalen Raumpunkt auf dem Boden (in Europa) einen Wert auf der z-Achse ("Höhe") zuordnet, der als Gefahr aufgrund radioaktiver Kontamination in Folge eines Reaktorunglücks zu verstehen ist. Dieser Gefahrenwert hängt direkt mit der Anzahl der zerfallenden Atomkernen zusammen, da die dabei entstehenden Teilchen Strahlenschäden in Zellen verursachen können.
In Anbetracht der vorherigen Modellierungszyklen wird bei der Modellierung der Gefahrenfunktion die Kontamination durch Cäsium-137 stellvertretend für alle radioaktive Nuklide berücksichtigt und ein nuklearer Fallout betrachtet.
Funktionsmodellierung für das Kraftwerk sowie einen nuklearen Fallout
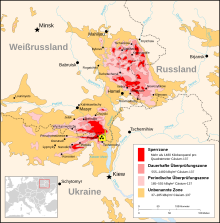
[Bearbeiten]In diesem ersten Modellierungsschritt soll eine Funktion gefunden werden, die das Risiko in der Nähe des Kraftwerks beschreibt. Außerdem bestimmen wir eine zweite Funktion , die das Risiko in der Nähe des Fallouts beschreibt. Diese beiden Funktionen und sind jeweils nur von zwei Messwerten abhängig. Die Messwerte können dann im konkreten Fall eines Reaktorunglücks erhoben werden oder mit Daten früherer Unfälle zur Aufklärung genutzt werden. Wir werden uns bei der Darstellung unserer Modellierungsfunktionen auf Messwerte des Unglücks in Tschernobyl beziehen (siehe dpa-Grafik: Radioaktivität in Europa nach Tschernobyl[7]).
Die Funktion modelliert dann als eindimensionale Funktion die Gefahr durch radioaktive Kontamination in Abhängigkeit des Abstands in Richtung des nuklearen Fallouts (Windrichtung).
Bestimmung der Funktionen f, g und u mit Hilfe von Maxima
[Bearbeiten]Zur Modellierung haben wir uns für eine gebrochenrationale Funktion der Form entschieden, da diese folgende Randbedingungen erfüllt:
- Einzige Extremstelle als Maximum
- Symmetrisch bzgl. dieses Maximums
- Stets positiv
- Stetig
- Lediglich von zwei Parametern abhängig, sodass sie durch zwei verschiedene Messwerte eindeutig bestimmbar ist
- Über Parameter a ist Höhe des Maximums (maximale Gefahr) veränderlich
- Über Parameter b ist Steigung (Breite des Gefahrenbereichs) veränderlich

Über die Punkte "Sperrzone" und "Kraftwerk" kann die Funktion parametrisiert werden. Konkrete Werte haben wir mithilfe einer Infografik des dpa[8] sowie den rechtsstehenden Maßstabsbetrachtungen aus jener Infografik ermittelt:
Kontamination in Tschernobyl: mind. Abstand zu Kraftwerk Tschernobyl: Kontamination Übergang dunkelrot/rot: Abstand zu Kernkraftwerk Tschernobyl: ca.
Mit diesen Punkten und der allgemeinen Funktion lassen sich zwei Gleichungen mit jeweils zwei Unbekannten bestimmen. Letztlich ergibt sich daraus dann die Funktion . Durch ähnliches Vorgehen bezüglich (beachte zusätzliche Verschiebung in x-Richtung um 1080km (siehe Zyklus 2 bei typischen Bedingungen)) lassen sich aus der Infografik die folgenden Punkte bestimmen:
Kontamination MittelpunktRegen: mind. Abstand zu Kraftwerk Tschernobyl: Kontamination Übergang orange/beige: Abstand zu Kernkraftwerk Tschernobyl: ca.
Dies führt dann zu Eine Funktion, die und superponiert, nähert das Risiko dann an. Jedoch ergibt sich ein kleiner Fehler bezüglich der Messwerte, da geringe Anteile von f bzw. von g die ursprünglichen Messwerte leicht erhöht. Bei großem Abstand der beiden Maxima ist diese Ungenauigkeit sehr gering. Dies wird im weiteren Verlauf der Modellierung gezeigt.
Eine akkuratere Endfunktion für das Risiko muss also durch folgende Punkte gehen:
Dies liefert folgende Gleichungen:
Man erhält ein nicht lineares Gleichungssystem mit 4 Unbekannten Variablen . Die Lösungen des Gleichungssystems wurden mit dem CAS-System Maxima ermittelt (vgl. unten) und lauten:

Wie hier zu sehen ist, sind die Abweichungen im Vergleich zum ursprünglichen Vorgehen nur geringfügig. Das erste Vorgehen erlaubt jedoch mehr Interaktivität, da Messwerte in der Geogebra-Datei einfach durch Bewegen der Punkte anzupassen sind, sodass man direkt einschätzen kann, wie die radioaktive Gefahr unter bestimmten Voraussetzungen ist. Eine Implementation des zweiten Ansatzes ist in Geogebra interaktiv nicht möglich, da das nicht lineare Gleichungssystem selbst in der CAS-Ansicht nicht richtig gelöst wird (siehe nebenstehende Abbildung). In Bezug auf unser Modellierungsziel - der Aufklärung von Bürgerinnen und Bürgern - werden wir im Folgenden daher mit den Werten des ersten Ansatzes fortfahren und die kleinen Abweichungen damit tolerieren. Diese führen nämlich sicherlich nicht dazu, dass das Risiko vollkommen falsch eingeschätzt wird.
Man erhält als Funktion somit:
Dabei wurde die gesamte Funktion aufgeteilt in zwei verschiedene Funktionen, die jeweils die Ursachen der Radioaktivität beschreiben. Es gilt:
In der Modellierung wird fortlaufend mit den gerundeten Werten (vgl. oben) gearbeitet. Dadurch beschreibt die Funktion zwar nicht exakt die Vorgaben, bleibt allerdings in Kombination mit den Messwerten und der obigen Graphik besser verständlich. Somit werden die Funktionen mit den gerundeten Werten mehr der Zielsetzung zur Bewusstseinsschaffung gerecht.

Dreidimensionale Erweiterung der Gefahrenfunktion
[Bearbeiten]Für das Modell in einem dreidimensionalen reellen Vektorraum können die Funktionen aus dem zweidimensionalen nahezu gleich übernommen werden. Für die Funktion, die das Risiko im Zentrum des Koordinatensystems, also dem Kernkraftwerk, angibt, muss das Argument der Funktion um die Variable y erweitert werden:
Analog folgt für die zweite Funktion, die das Risiko durch abgeregnete Nuklide modelliert:
Hier wird angenommen, dass die Windrichtung, die eine Wolke mit radioaktivem Material bewegt entlang der positiven Windrichtung weht. Für verschiedene Windrichtungen kann in Analogie zu dem Modellierungszyklus der Sekundarstufe 2 eine Darstellung in Abhängigkeit des Winkels verwendet werden: .
Die Windrichtung kann dabei durch den Winkel im Bereich von bzw. 0 bis 360 Grad eingestellt werden. Die Gesamtfunktion ergibt sich dann als Summe der beiden Funktionen:
Berücksichtigung der zeitlichen Komponente
[Bearbeiten]Um den radioaktiven Zerfall in der Modellierung zu berücksichtigen, wird der Zähler, der einer radioaktiven Belastung entspricht, mit einer exponentiellen Zerfallsfunktion multipliziert: . Die Konstante ist dabei die Zerfallskonstante des jeweiligen Atoms. Wir betrachten analog zu Zyklus 1 Cs-137 mit einer Halbwertszeit von ca. 30 Jahren, und damit folgt: . Somit erhält man insgesamt
Letztlich erhält man also eine Funktion die in ihrem Ausgabewert abhängig von 4 Eingabewerten ist.
Computergestützte Umsetzung
[Bearbeiten]
Die Funktionen können sowohl im zwei- als auch im dreidimensionalen mit Hilfe von GeoGebra visualisiert werden. Mit Hilfe von Schiebereglern kann dabei die Windrichtung, aber auch die Zeit variiert werden, wodurch die Abhängigkeiten und Zusammenhänge dynamisch veranschaulicht werden. Die jeweiligen Funktionen werden in GeoGebra genau wie in der obigen mathematischen Herleitung definiert, wobei und über das Einfügen von Schiebereglern definiert werden.
Die Modellierung kann aber auch in einem Computer-Algebra-System realisiert werden: Dazu kann beispielsweise (Wx)Maxima verwendet werden. Hier werden Funktionen im dreidimensionalen mit Gitternetzlinien dargestellt, was die dreidimensionale Wahrnehmung vereinfacht. Zusätzlich wird die Ausgabevariable je nach Betrag farbig dargestellt. Allerdings muss sich hier auf eine Zeit, sowie Windrichtung festgelegt werden, bevor der Plot erstellt wird. Daher wird sich in dieser Umsetzung auf die Funktionen bezogen, die weder die Zeitabhängigkeit, noch die Windrichtung berücksichtigen. Die Eingaben in Maxima lauten:
f(x,y):=(1480)/(1+(7/10000)*(x^2+y^2)); g(x,y):=(40)/(1+(1/7500)*((x-1080)^2+(y)^2)); u(x,y):= f(x,y)+g(x,y);
Um die Funktion graphisch darzustellen wird der Code wxplot3d verwendet. Konkret: wxplot3d(u(x,y),[x,-100,1300],[y,-1000,1000],[grid,100,100]); (Alternativ wxplot3d(f(x,y)+g(x,y),[x,-100,1300],[y,-1000,1000],[grid,100,100]); )
Die erste Eingabe definiert die zu plottende Funktion. Die zweite und dritte Eingabe definieren die Variablen und die Bereiche, in denen die Funktion ausgewertet werden soll. Durch die Ergänzung [grid,100,100] werden die Feldlinien, entlang derer die Funktion ausgewertet wird, enger dargestellt, wodurch der Graph im Gesamten stetiger aussieht. Man erhält somit folgendes Bild:

Wie oben bereits erwähnt werden die Koeffizienten der Funktionen durch ein nicht-lineares Gleichungssystem mittels WxMaxima gelöst. Dabei werden folgende Codes verwendet:
--> gl1: 1480=a1/(1+b1*(0^2))+a2/(1+b2*(0-1080)^2); --> gl2: 185=a1/(1+b1*(100^2))+a2/(1+b2*(100-1080)^2); --> gl3: 10=a1/(1+b1*(930^2))+a2/(1+b2*(930-1080)^2); --> gl4: 40=a1/(1+b1*(1080^2))+a2/(1+b2*(1080-1080)^2); --> solve([gl1,gl2,gl3,gl4],[a1,a2,b1,b2]);
Die Plotfunktion in Maxima lässt sich außerdem dazu nutzen, die akkuratere Endfunktion, die die Messwerte tatsächlich beschreiben, darzustellen. Dazu wurden die Parameter des Gleichungssystems in Maxima ausgelesen und dann wiederum geplottet. Zur besseren Erkennbarkeit des Risikos durch den Fallout wurde außerdem eine Farbanpassung des Graphen vorgenommen, sodass auch kleinere Veränderungen der Risikowerte farblich stärker hervorgehoben werden. Der Maxima-Code zur Erstellung dieser akkuraten Funktion lautet wie folgt:
gl1: 1480=a1/(1+b1*(0^2))+a2/(1+b2*(0-1080)^2); gl2: 185=a1/(1+b1*(100^2))+a2/(1+b2*(100-1080)^2); gl3: 10=a1/(1+b1*(930^2))+a2/(1+b2*(930-1080)^2); gl4: 40=a1/(1+b1*(1080^2))+a2/(1+b2*(1080-1080)^2); GS: solve([gl1,gl2,gl3,gl4],[a1,a2,b1,b2]); a1: rhs(GS[4][1]); a2: rhs(GS[4][2]); b1: rhs(GS[4][3]); b2: rhs(GS[4][4]); u(x):=(a1)/(1+(b1)*(x^2+y^2))+(a2)/(1+b2*((x-1080)^2+(y)^2)); plot3d(u(x),[x,-400,1300],[y,-500,500],[z,0,700],[grid,80,80], [zlabel, "Risiko"],[palette, [gradient, yellow, green, cyan, cyan, blue, blue, blue, magenta, magenta, magenta, magenta, red, red, red, red, red]]);
Nach betätigen der Schaltfläche "apply autoscale" in GnuPlot ergibt sich untenstehende Funktion

Resultate der Modellierung
[Bearbeiten]Das Endresultat der Modellierung ist die Darstellung einer Gefahrenfunktion , die das zeitliche und räumliche Gefahrenpotential eines Nuklearunfalls unter Berücksichtigung eines nuklearen Wash-Outs beschreibt. In Geogebra kann darüber hinaus das Risiko in Windabhängigkeit und im zeitlichen Verlauf nach der Katastrophe interaktiv visualisiert werden. Durch den mit Hilfe von WxMaxima gezeigten Graphen wird das Risiko deutlich visualisiert. Besonders beachtenswert ist das globale Maximum am Ort des Kraftwerks und das hohe Risiko in seiner Umgebung. Im Vergleich zu diesem wirkt das lokale Maximum des Risikos sowie in dessen umliegenden Bereich (in dem es zum nuklearen Fallout kommt) vernachlässigbar klein.
Resultate in Realsituation
[Bearbeiten]Dies ist jedoch in der Realität keinesfalls vernachlässigbar. Die Menge an radioaktiver Belastung und dem damit verknüpften Risiko kann (wie wir an unseren Daten aus Zyklus 1 und den Auswirkungen von Tschernobyl sehen) noch jahrzehntelang zu gesundheitlichen Gefahren führen. Die Belastung im Umfeld des Kernkraftwerks ist jedoch so groß, dass die Radioaktivität Menschen nicht durch Mutationen langfristig schadet, sondern unmittelbar nach dem Unglück innerhalb weniger Minuten oder Stunden töten kann. Über allgemeinere Resultate in einer Realsituation lässt sich aktuell wenig sagen. Glücklicherweise gab es bis heute nämlich erst zwei größere Reaktorunglücke: in Tschernobyl und in Fukushima. Die Modellierung selbst stützt sich auf Daten von Tschernobyl und modelliert die dortige Situation entsprechend adäquat. Die Anwendbarkeit auf Fukushima ist dahingehend problematisch, da es in Fukushima zu keinem nuklearen Fallout aufgrund von radioaktivem Niederschlag über dem Festland kam. Die radioaktiven Partikel wurden nämlich in den ersten Tagen in Windrichtung über den Pazifik verteilt [9]. Ein dortiges Abregnen ist zwar wahrscheinlich, jedoch nicht durch Daten belegbar. Durch die Meeresströmungen würden die Partikel im Falle eines Niederschlags über einen großen Meeresbereich verteilt werden. Nach den ersten Tagen kam es in Japan auch vereinzelt zu radioaktivem Niederschlag, jedoch kann man in diesem Fall dann nicht von einer annähernd konstanten Windrichtung ausgehen, da Zyklone Ursache des Windes waren[10].
Bewertung & Optimierung
[Bearbeiten]Dieser Modellierungszyklus verbindet mit nur einer einzigen Funktion die zeitlichen und räumlichen Risken in Folge einer Nuklearkatastrophe. Bei Betrachtung des Graphen kann jedoch der Eindruck entstehen, dass ein Risiko nur in unmittelbarer Nähe zum Reaktor vorhanden ist, da der dortige Risikowert um ein Vielfaches höher ist als überall sonst und insbesondere auch dort, wo radioaktiver Niederschlag zu Boden fällt. In der Realität ist die dortige Strahlenbelastung jedoch so groß, dass Sperrzonen gebildet werden müssen, da auch nur ein kurzer Aufenthalt innerhalb dieses so risikoreichen Gebiets zum Tod führen kann. Die enorme Belastung an dem Kraftwerk selbst sorgt daher für eine Skalierung, die nicht mit den Vorstellungen und Gegebenheiten der vergangenen Katastrophen übereinstimmt, auch wenn die Modellierung an sich adäquat dazu passt. Das Risiko außerhalb ist - nur wegen der enormen Belastung innerhalb der Sperrzone - definitiv nicht vernachlässigbar (zum Vergleich: Bodenbelastung im Nebenmaximum in unserem Beispiel: , Luft unter Normalbedingungen: ). Das kleine Maximum durch den radioaktiven Niederschlag führt noch heute dazu, dass beispielsweise Rotwild aus Südbayern nicht ohne Weiteres konsumiert werden kann, da es eine potentiell gefährliche radioaktive Belastung des Körpers zur Folge haben könnte. Diese Tatsache sollte bei Betrachtung der Modellierung also definitiv herausgestellt werden.
Aufgrund der hohen Komplexität der Zerfallsprozesse und der Verbreitung von Stoffen - und damit auch radioaktiven Nukliden - in der Luft gibt es zahlreiche Möglichkeiten der Optimierung, die zeitbedingt jedoch nicht weiter mit einbezogen werden können:
- Beachtung wechselnder Luftströmungen bzw. Windrichtungen und verschiedener Windstärken in zeitlicher Abhängigkeit
- Diffusionsprozesse in der Luft, wodurch die Ausbreitung der radioaktiven Wolke modelliert werden kann
- Herabsinken der Nuklide aufgrund der Gravitation, sodass das gesamte Gebiet in Windrichtung stärkere radioaktive Belastung aufweist als andere Richtungen
- Zeitlicher Einfluss aller anderen Nuklide und deren Spaltprodukte (nicht nur Cs-137)
- ...
Wiki2Reveal
[Bearbeiten]Bezüge zu anderen Modellierungsprojekten
[Bearbeiten]- https://de.wikiversity.org/wiki/Kurs:Mathematische_Modellbildung/Themen/Stromerzeugung_durch_kinetische_Energie#Niveauzuordnung
- BA-Arbeit: Modellierung der Dynamik von radioaktiven Expositionskarten zur Risikominimierung
Gruppenmitglieder
[Bearbeiten]- Isabelle Heringer
- Michelle Welter
- Jonah Schuster
- Noah Buchmann
Quellen/Literatur
[Bearbeiten]- ↑ a b c d e Giancoli, D. C. (2019). Physik: Lehr-und Übungsbuch. 4., akutalisierte Auflage. Pearson Deutschland GmbH.
- ↑ UNSCEAR 2008 Report. Sources and effects of ionizing radiation. Band 2. Annex D – Health effects due to radiation from the Chernobyl accident. New York 2011, S. 49, online (PDF; 5,3 MB)
- ↑ Aoyama, Michio (2018): Long-range transport of radiocaesium derived from global fallout and the Fukushima accident in the Pacific Ocean since 1953 through 2017-Part I: Source term and surface transport. In: J Radioanal Nucl Chem 318 (3), S. 1519–1542. DOI: 10.1007/s10967-018-6244-z.
- ↑ Seite „Radioaktiver Niederschlag“. In: Wikipedia – Die freie Enzyklopädie. Bearbeitungsstand: 22. Dezember 2021, 03:52 UTC. URL: https://de.wikipedia.org/w/index.php?title=Radioaktiver_Niederschlag&oldid=218402971 (Abgerufen: 23. Dezember 2021, 08:02 UTC)
- ↑ Alexey V. Yablokov, Vassily B. Nesterenko, Alexey V. Nesterenko: Chernobyl: Consequences of the Catastrophe for People and the Environment. In: Annals of the New York Academy of Sciences. Band 1181, 2009, S. 5, PDF (Memento vom 8. Oktober 2012 im Internet Archive)
- ↑ Bundesamt für Strahlenschutz (20221), Umweltkontaminationen und weitere Folgen des Reaktorunfalls von Tschernobyl - URL: https://www.bfs.de/DE/themen/ion/notfallschutz/notfall/tschernobyl/umweltfolgen.html (Zugriff: 23.12.2021)
- ↑ Bayernkurier (2016): Was von Tschernobyl übrig blieb - Bayernkurier. Online verfügbar unter https://www.bayernkurier.de/inland/13008-was-von-tschernobyl-uebrig-blieb/, zuletzt aktualisiert am 01.02.2019, zuletzt geprüft am 31.01.2022.
- ↑ Bayernkurier (2016): Was von Tschernobyl übrig blieb - Bayernkurier. Online verfügbar unter https://www.bayernkurier.de/inland/13008-was-von-tschernobyl-uebrig-blieb/, zuletzt aktualisiert am 01.02.2019, zuletzt geprüft am 31.01.2022.
- ↑ Erstes Deutsches Fernsehen (ARD) (2022): Rätsel um Radioaktivität | W wie Wissen. DasErste.de. Online verfügbar unter https://www.daserste.de/information/wissen-kultur/w-wie-wissen/sendung/2012/raetsel-um-radioaktivitaet-100.html, zuletzt aktualisiert am 01.02.2022, zuletzt geprüft am 01.02.2022.
- ↑ Erstes Deutsches Fernsehen (ARD) (2022): Rätsel um Radioaktivität | W wie Wissen. DasErste.de. Online verfügbar unter https://www.daserste.de/information/wissen-kultur/w-wie-wissen/sendung/2012/raetsel-um-radioaktivitaet-100.html, zuletzt aktualisiert am 01.02.2022, zuletzt geprüft am 01.02.2022.




















































![{\displaystyle \left[0,360\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb5892102a0e28d379efbb340c08dc461c0e2b87)







































![{\displaystyle \left[0;2\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c978eb3538e1f23896cef40bc7563ee44f7356e5)








