Kurs:Mathematische Modellbildung/Themen/Radioaktivität und Risikoliteralität/Modellierungszyklen
Allgemeine Ziele
[Bearbeiten]- Ziel: Risikobewusstsein für die Gefahren radioaktiver Strahlung erhöhen
- Erster Modellierungszyklus: Fokussierung auf Zeitaspekt
- Zweiter Modellierungszyklus: Fokussierung auf die räumliche Gefahr, die von Atomkraftwerken ausgeht
- Dritter Modellierungszyklus: Verbindung der zeitlichen und räumlichen Gefahr
- ⇒ Aufklärung der SchülerInnen bzw. BürgerInnen um Risiken und Nutzen von Kernenergie abwägen zu können
- Allgemeine Diskussion Politik über Nutzung von Kernkraftwerken als Alternative zur Kohlekraftwerken
Modellierungszyklus 1 - Sekundarstufe 1
[Bearbeiten]- Modellierung des exponentiellen Zerfalls von radioaktiven Stoffen
- Veranschaulichung der zeitlichen Spanne, die Zerfallsprozesse einnehmen können
Ziel
[Bearbeiten]- Bewusstsein für Radioaktivität schaffen
- Zufallsgesteuerten Prozess sichtbar machen
⇒ Ergibt e-Funktion
Inhaltliche Beschreibung
[Bearbeiten]- Betrachtung einer großen Anzahl radioaktiver Nuklide, die mit einer gewissen Wahrscheinlichkeit zerfallen
- Feste Zeitintervalle mit einer jeweils konstanten Zerfallswahrscheinlichkeit
- Plotten der Anzahl zerfallener Nuklide in Abhängigkeit von der Zeit
- Vergleich mit einer realen Zerfallskurve (durch Halbwertszeit und Anfangsanzahl)
- Zufallsexperiment: Würfelmodell SuS sammeln erste Erfahrungen mit Radioaktivität und radioaktivem Zerfall
- Material: Vorgegebene Anzahl an Würfeln
- Anzahl der Würfel = Anzahl radioaktiver Teilchen
Mathematisches Modell
[Bearbeiten]- Laplace Experiment: Würfelwurf
- Ergebnismenge
- Wahrscheinlichkeit für das Ereignis eine bestimmte Augenzahl zu würfeln
- Wahrscheinlichkeit für das Ereignis einer anderen Augenzahlen
- Nach dem ersten Wurf: Anzahl der verbleibenden Würfel = Anzahl aller Würfel • Wahrscheinlichkeit keine 6 zu würfeln
- Anzahl der verbleibenden Würfel nach dem n-ten Wurf bei Würfel zu Beginn: .
Schlussfolgerung
[Bearbeiten]- Gleichung ähnelt Exponentialgleichung
- Exponentielle Abnahme: mit Zeitspanne und dem Wert der Größe zu Beginn
Konkretes Vorgehen
[Bearbeiten]- Schritt 1: Festlegen einer Augenzahl(z.B. 6) und Würfeln aller Würfel
- Schritt 2: Entfernen aller Würfel mit der Augenzahl 6
- Schritt 3: Anzahl der zu entfernenden und verbleibenden Würfeln in eine Tabelle eintragen
- Anzahl zu entfernende Würfel= Anzahl der zerfallenen radioaktiven Teilchen
- Anzahl verbleibende Würfel = noch vorhandene radioaktive Teilchen
- Schritt 2 und 3 werden solange wiederholt bis keine Würfel mehr übrig sind
Software
[Bearbeiten]Tabellenkalkulation mit LibreOffice Calc

Beschreibung
[Bearbeiten]- Anzahl der Startatome = Anzahl der Zeilen
- Codierung der Spalten: Atom zerfallen = 1 ; Atom noch vorhanden = 0
Erster Zeitschritt
[Bearbeiten]- Zuweisung 0 oder 1 durch Auswertung einer Zufallszahl in einem festgelegten Bereich (hier: 1 bis 6)
- Auswertung der Zufallszahl über WENN-Befehl
WENN(ZUFALLSBEREICH(1;$C$1)=6;1;0)
- Zufallszahl = 6 ⇒ Atom zerfallen ⇒ Codierung in Spalte mit 1 (Zufallszahl ≠ 6 ⇒Codierung mit 0 ⇒ Atom noch vorhanden)
- In der nächsten Spalte werden alle noch vorhandenen Atome durch ihre Startnummer (=Nummer Zeile) repräsentiert
- Durch WENN-Abfrage wird den zerfallenen Atomen der Ausdruck "Zerfallen" zugeordnet
WENN(B3=0;A3;"Zerfallen")
⇒ Ablesen der noch vorhandenen Atome (alle 0 - Werte) in unterster Zeile (ZÄHLENWENN-Befehl)
Nächster Zeitschritt
[Bearbeiten]- Atome, die schon zerfallen sind bekommen Wert 1 zugeordenet
- Noch vorhandene Atome: Wiederholung 1. Zeitschritt
- Zuordnung einer neuen Zufallszahl
- Auswertung der Zufallszahlen über WENN-Abfrage
WENN(ODER(ZUFALLSBEREICH(1;$C$1)=6;C3="Zerfallen");1;0)
- Durch WENN-Abfrage wird den zerfallenen Atomen der Ausdruck "Zerfallen" zugeordnet
WENN(D3=0;C3;"Zerfallen")
⇒ Ablesen der noch vorhandenen Atome in unterster Zeile (ZÄHLENWENN-Befehl)
- Analoges Vorgehen für weitere Zeitschritte bis alle Atome zerfallen, also in allen Zeilen der Ausdruck Zerfallen steht.
Resultate der Modellierung
[Bearbeiten]

Resultate in Realsituation
[Bearbeiten]- Zerfall = Zufallsprozess, aber Zerfallswahrscheinlichkeit ≠ Wahrscheinlichkeit Würfelwurf
- Genaue Vorhersage, wann ein bestimmter Kern zerfällt nicht möglich, lediglich Abschätzung
- Eine Probe eines radioaktiven Isotops besteht aus einer großen Menge radioaktiver Kerne ⇒ Diese Kerne zerfallen nicht alle gleichzeitig, sondern innerhalb eines gewissen Zeitintervalls
Resultate I
[Bearbeiten]- Anzahl der in einem sehr kurzen Zeitintervall stattfindenden Zerfälle ist proportional zu und der der Gesamtzahl der vorhandenen radioaktiven Kerne:
- : Zerfallskonstante, die je nach Nuklid unterschiedliche Werte annimmt
- : Anzahl der in dem Zeitintervall stattfindenden Zerfälle
Resultate II
[Bearbeiten]- Zerfallsgesetz:
- Integrationskonstante : Anzahl der zur Zeit vorhandenen Mutterkerne
- N: Anzahl der verbliebenen Kerne
- Radioaktive Zerfallsgesetz besagt, dass die Anzahl der radioaktiven Kerne in einer gegebenen Probe mit der Zeit exponentiell abfällt ⇒ Beschreibung eines radioaktiven Zerfalls mithilfe der Exponentialfunktion
Resultate III
[Bearbeiten]- Mit bei ergibt sich dadurch:
- Aus ergibt sich durch logarithmieren für die Halbwertszeit: .
- Insgesamt ergibt sich damit für die Funktion zur mathematischen Beschreibung des radioaktiven Zerfalls
- Bezug zur Modellierung im Sinne des Würfelversuch: Halbwertszeit, also die Zeit nach der noch die Hälfte der ursprünglichen Anzahl radioaktiver Teilchen vorhanden ist, kann aus den erhobenen Daten ermittelt werden
Zerfall von Cs-137
[Bearbeiten]- Nuklearkatastrophe Tschernobyl: Cs-137 am stärksten radioaktiv strahlendes Nuklid
- Halbwertszeit: ca. 30 Jahre
- Nach Modellierungszyklus 1:
- Betrachtete Modellierung: 4 Halbwertszeiten (120 Jahre)
- Bei 50 Startatome wären am Ende der Modellierung immer noch Atome übrig
Atommüll
[Bearbeiten]- Weist meist lang strahlende Nuklidanteile auf
- Z.B.: Iod-129 Halbwertszeit von Jahre
- Muss sichergestellt werden, dass nichts ins Grundwasser oder Atmosphäre gelangt → starke Genmutationen (Krebs als Folge)
Bewertung und Optimierung
[Bearbeiten]- Annahme Modellierung: Teilchen sind nach dem Zerfall nicht mehr vorhanden
- Realität: Zerfallsketten
- Modellierungsprozess nur 50 Nuklide ↔ Realität deutlich höhere Anzahl an Teilchen (1 kg Cs enthält 10^34)
- Örtliche Komponente wird im Modellierungszyklus 1 nicht betrachtet ⇒ Optimierung in Modellierungszyklus 2
- Beispiel: Fukushima, nach Fallout gelangen radioaktive Teilchen in die Luft und Wolken und wurden durch Winde über den Pazifik getragen ⇒ trotz großer räumlicher Distanz weit entfernte Gebiete deutlich höhere radioaktive Belastung als z.B. das nahegelegene Korea
Vorteile Tabellenkalkulation
[Bearbeiten]- Vertrautheit der SuS
- Direktes übertragen eigener Messergebnisse in die Tabelle sowie direkte Auswertung
- Ziel der Visualisierung des zufallsgesteuerten Prozess mit Ergebnis einer e-Funktion wird erfüllt
Modellierungszyklus 2 - Sekundarstufe 2
[Bearbeiten]Ziel
[Bearbeiten]- Bewusstsein für Radioaktivität schaffen
- Erkenntnisse zu räumlicher Ausdehnung und Verbreitung von radioaktivem Material
Inhaltliche Beschreibung
[Bearbeiten]- Modellierung: Flugbahn einer radioaktiven Wolke und anschließendem Fallout mit Startpunkt in Philippsburg
Idealisierungen/ Annahmen
[Bearbeiten]- Starthöhe Wolke nach Kernreaktorkatastrophe: 12 km
- Windgeschwindigkeit konstant: (Durchschnitt in Philippsburg)
- Wolke = Punkt → Regen fällt auf einen Punkt
- Bis zum Fallout: Wolke auf konstanter Starthöhe von 12km
- Fallgeschwindigkeit des Regens konstant:
Variablen
[Bearbeiten]- Windrichtung α
- Zeiteinheit , in der die Wolke weggetragen wird
- Punkt , in dem sich die Wolke zum Zeitpunkt befindet
- Zeit des Abregnens
Bezeichnungen
[Bearbeiten]- : Startpunkt
- : Position der Wolke
- : Auftreffpunkt des Regens
- : Windgeschwindigkeit + Windrichtung
- : Fallgeschwindigkeit
Mathematisches Modell
[Bearbeiten]- Grundlage: Vektoranalysis bzw. Analytische Geometrie Sek II
- Punkte und Linearkombinationen im dreidimensionalen reellen Vektorraum
1. Bahnkurve der Wolke erstellen:
[Bearbeiten]- Startpunkt
- Zeit seit Beginn der Bewegung
- Windvektor (konst. Windgeschwindigkeit + variable Windrichtung)
- Aufenthaltspunkt der Wolke:
2. Neue Bahnkurve ab Fallout:
[Bearbeiten]- Position
- Zeit des Abregnens
- Windvektor
- Fallgeschwindigkeit Regen (konstant)
- Auftreffpunkt des Regens:
Software
[Bearbeiten]Geogebra
- Vorteil: Parallele und dynamische Darstellung von Objekten in einem 2-dimensionalen + 3-dimensionalen Koordinatensystem
- Europakarte einfügen zur besseren Veranschaulichung am Beispiel Philippsburg bzw. Ausbreitung in Europa
Konstruktionsprotokoll
[Bearbeiten]
Modellierung im 2-dimensionalen Raum
[Bearbeiten]
Modellierung im 3-dimensionalen Raum
[Bearbeiten]
Resultate der Modellierung
[Bearbeiten]- Ort des Niederschlags nach einer Kernschmelze berechenbar und darstellbar
- Betrachtung des Startpunktes Kraftwerk Philippsburg
- Mittelpunkt der Wolke und somit des Niederschlags kann bestimmt werden
- Aufgrund geographischer Lage wird von einem Westwind ausgegangen, Mittelwert Philippsburg 15 km/h
- Im Durchschnitt regnet es jeden dritten Tag in Europa
- Ergebnis: Niederschlag an slowakisch-ukrainischer Grenze
- Darstellung aller Möglichkeiten nach 72h kann als Spur (Kreis) dargestellt werden
Ansicht der möglichen Auftreffpunkte des radioaktiven Niederschlags
[Bearbeiten]- Tool zur Bestimmung des Herabregnens radioaktiver Nuklide in Abhängigkeit von Zeit und Wind (Richtung+Geschwindigkeit)

Resultate in Realsituation
[Bearbeiten]Beispiel Fukushima: Abhängigkeit zwischen radioaktiver Verschmutzung und Windrichtung
[Bearbeiten]- Abhängigkeit von der Windrichtung: radioaktive Verschmutzung am Boden stärker von Windrichtung abhängig als vom radialen Abstand zum Atomreaktor (Kontamination nicht gleichmäßig in alle Richtungen um Reaktor)
- Abhängigkeit von Ort des Fallouts (=Staub gelangt in Atmosphäre (radioaktive Aerosole)→ durch Abregnen gelangen radioaktive Teilchen auf Erdoberfläche)
- Sonderform Washout: Radioaktive Teilchhen fallen von oben auf Wolkendecke und vereinigen sich mit Regentropfen, durch Regen fallen sie zu Boden und es kommt in großen Entfernungen zu radioaktiver Belastung
Grafik geschätzte radioaktive Dosis im ersten Jahr nach dem Reaktorunglück in Fukushima
[Bearbeiten]
Beispiel Tschernobyl:
[Bearbeiten]- Durch Kernschmelze+Explosion kam es zu Graphitbrand → gasförmige/leicht flüchtige Stoffe wie Jod und Cäsium gelangten in 3,5 - 10km Höhe
- Über radioaktive Wolke und anschließendes Abregnen → Radionuklide von Polen bis Skandinavien
- Zweite Wolke verteilt Nuklide von Slowakei, Tscheschien, Österreich bis nach Deutschland → Folgen heute noch spürbar (Verseuchung von Wild in Süddeutschland)
- Dritte Wolke: Rumänien, Bulgarien, Griechenland, Türkei
Cäsium-137-Kontamination im Jahr 1996
[Bearbeiten]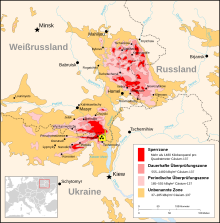
Bewertung und Optimierung
[Bearbeiten]Annahmen I
[Bearbeiten]- 1. Modellierung Wolke als Punkt keine zu vernachlässigende Vereinfachung dar → besser: Modellierung als Kugel oder Ellipsoid → größeres kontaminiertes Gebiet darstellbar
- Kugel würde sich mit zunehmender Zeit vergrößern aufgrund von Diffussionsprozessen (Abnahme der Partikeldichte)
- 2. Starthöhe = fester Punkt: Starthöhe könnte in Realsituation eine andere sein, führt zu anderen Werten + radioaktive Partikel befinden sich auf unterschiedlichen Höhen. Annahme: Gesamtheit vereinigt sich in einem einzigen Punkt nicht vernachlässigbar
Annahmen II
[Bearbeiten]- 3. Radioaktive Partikel sinken vor Abregnen nicht zu Boden, bewegen sich parallel zum Boden → nicht vernachlässigbarer Teil der Verschmutzung wird nicht berücksichtigt
- 4. Konstante Windrichtung + Konstante Fallgeschwindigkeit: Wind bleibt in Betrag und Richtung konstant (gleiches gilt für Fallgeschwindigkeit Regen)
- 5. Zeitliche Dauer der Freisetzung: Partikel befinden sich bereits in der Luft und es werden keine weiteren freigesetzt (vgl. Tschernobyl/Fukushima) = Kernexplosion wird beschrieben
- 6. Geographische Gegebenheiten werden nicht beachtet: bspw. Steigungsregen an den Alpen wird in Modellierung nicht beachtet
Ziel:
[Bearbeiten]Räumliche Verbreitung und Ausdehnung von radioaktivem Material wird sichtbar ⇒ daher Entscheidung für allgemeine Variante bei der Geographische Gegebenheiten nicht berücksichtigt werden
Vorteile Geogebra:
[Bearbeiten]Gleichzeitige Darstellung in 2D und 3D sowie Schieberegler → SuS können Zusammenhänge selbst entdecken und verstehen lernen
Modellierungszyklus 3 - Universitäts Niveau
[Bearbeiten]Ziel
[Bearbeiten]- Zeitliche + Räumliche Modellierung aus den ersten beiden Zyklen miteinander verbinden ⇒ Die Gefahr einer Kernschmelze möglichst genau darstellen und somit über die Gefahren aufklären
- Zielgruppe: Alle Bürger:innen
- Möglichkeit mit Hilfe von Wetterdaten radioaktive Kontamination bei einem Reaktorunglück zeitlich und räumlich abschätzen zu können
Inhaltliche Beschreibung
[Bearbeiten]Grundlegende Annahmen
[Bearbeiten]- Die Modellierung bezieht sich auf den Zustand nach dem Abregnen der Wolke
- Bis zum Abregnen der Wolke keine radioaktiven Verluste
- Abregnen der Wolke nur in einem Gebiet
- Alle radioaktiven Materialien haben sich bereits abgesetzt
- ⇒ Alle Tansportprozesse sind bereits abgeschlossen!
Umsetzung
[Bearbeiten]- Funktion modellieren, die jedem zweidimensionalen Raumpunkt auf dem Boden einen Wert auf der z-Achse zuordnet
- z-Achse gibt Gefahrenwert aufgrund radioaktiver Kontamination in Folge eines Reaktorunglücks an
- Gefahrenwert abhängig von der Anzahl der zerfallenden Atomkerne (vgl. Zyklus 1)
- Gefahrenfunktion durch Kontamination mit Cäsium-137
Funktionsmodellierung für das Kraftwerk sowie einen nuklearen Fallout
[Bearbeiten]Erster Modellierungsschritt
[Bearbeiten]- Funktion finden, die das Risiko in der Nähe des Kraftwerks beschreibt
- Funktion finden, die Risiko in der Nähe des Fallouts beschreibt
- Abhängigkeit der Funktionen jeweils von zwei Messwerten, welche im konkreten Fall eines Reaktorunglücks erhoben werden oder mit Daten von früheren Unfällen zur Aufklärung genutzt werden
- Im Falle dieser Modellierung: Daten Unglück Tschernobyl
→ Funktion modelliert dann als eindimensionale Funktion die Gefahr durch radioaktive Kontamination in Abhängigkeit des Abstandes in Richtung des nuklearen Fallout (Windrichtung)
Zweiter Modellierungsschritt
[Bearbeiten]Bestimmung einer exakteren Gefahrenfunktion :
- Bestimmung der Messwerte analog zum ersten Vorgehen
- Koeffizienten der Funktion durch Lösen eines nicht-linearen Gleichungssystems
Bestimmung der Funktionen
[Bearbeiten]Gebrochen rationale Funktion der Form:
Begründung: Erfüllung folgender Randbedingungen
- Einzige Extremstelle als Maximum
- Symmetrisch bzgl. dieses Maximums
- Stets positiv
- Stetig
- Lediglich von zwei Parametern abhängig, sodass sie durch zwei verschiedene Messwerte eindeutig bestimmbar ist
Parameter
[Bearbeiten]- Über Parameter a ist Höhe des Maximums (maximale Gefahr) veränderlich
- Über Parameter b ist Steigung (Breite des Gefahrenbereichs) veränderlich
Bestimmung der Funktion f
[Bearbeiten]- Über Punkte "Sperrzone" und "Kraftwerk" kann die Funktion f parametrisiert werden (konkrete Werte über Infografik des dpa)
Ermittlung der erforderlichen Daten aus Infografik
[Bearbeiten]1. Punkt Kraftwerk:
[Bearbeiten]- Größte Belastung am Kraftwerk: mind. → y-Wert des Kraftwerkes 1480
- Abstand zum Kraftwerk Tschernobyl: → x-Wert des Kraftwerkes 0
- → Punkt Kraftwerk eindeutig bestimmt: (0 | 1480)
2. Punkt Sperrzone:
[Bearbeiten]- Hier wird der Übergang der Karte von dunkelrot zu rot genommen
- Belastung liegt bei → y-Wert der Sperrzone 185
- Abstand zum Kraftwerk Tschernobyl (nach Maßstab der Infografik): ca. → x-Wert 100
- → Punkt Sperrzone eindeutig bestimmt: (100 | 185)
Erhalt der Funktion f
[Bearbeiten]- Mit den ermittelten Punkten und der allgemeinen Funktion lassen sich zwei Gleichungen mit jeweils zwei Unbekannten bestimmen
- Lösen des Linearen Gleichungssystems
- Einsetzen in gebrochen rationale Funktion:
Bestimmung Funktion g
[Bearbeiten]1. Punkt Mittelpunkt der Abregnung:
[Bearbeiten]- Radialer Abstand vom Kraftwerk zum Mittelpunkt der Abregnung entspricht ca. nach (vgl. Zyklus 2)
- Größte Belastung am Abregnungspunkt: mind. → y-Wert des Mittelpunkts der Abregnung 40
- Abstand zum Kraftwerk Tschernobyl: → x-Wert des Mittelpunkts der Abregnung 1080
- → Punkt Mittelpunkt der Abregnung eindeutig bestimmt: (1080 | 40)
2. Punkt Messwert Regen:
[Bearbeiten]- Hier wird der Übergang der Karte von orange zu beige
- Belastung liegt bei → y-Wert des Messpunkt des Regens 10
- Abstand zum Kraftwerk Tschernobyl → x-Wert 930
- → Punkt Messwert des Regens eindeutig bestimmt ( 930 | 10)
- Führt analog wie bei der Ermittlung von f zu:
Bestimmung Funktion u durch Superposition
[Bearbeiten]Gefahrenfunktion im Zweidimensionalen durch Superposition der beiden Funktionen f und g:

Optimierung der Gefahrenfunktion u
[Bearbeiten]- Eine Funktion, die f und g superponiert, näher das Risiko an, jedoch ergibt sich ein kleiner Fehler bezüglich der Messwerte
- Die ursprünglichen Messwerte werden dadurch leicht erhöht
- Bei großem Abstand der Maxima ist diese Ungenauigkeit allerdings sehr gering
Exaktere Bestimmung der Gefahrenfunktion u
[Bearbeiten]- Die Funktion müsste durch die folgenden Punkte gehen:
- Daraus ergibt sich mit den ermittelten Messwerten (bestimmte Punkte, siehe oben) das folgende nicht-lineare Gleichungssytem mit 4 Unbekannten :
Lösung des Gleichungssystems mithilfe von Maxima
[Bearbeiten]
Schlussfolgerung
[Bearbeiten]- Abweichungen im Vergleich zum ursprünglichen Vorgehen vernachlässigbar
- Erstes Vorgehen erlaubt jedoch mehr Interaktivität
- Einfaches Anpassen der Messwerte durch Bewegen der Punkte
- Radioaktive Gefahr unter bestimmten Voraussetzungen anschaulicher
- Implementation des zweiten Ansatzes in Geogebra nicht möglich, da das nicht-lineare Gleichungssystem nicht exakt genug gelöst wird
- Bezug zum Modellierungsziel der Aufklärung und Bewusstseinsschaffung der Bürger:innen: Werte des ersten Ansatzes anschaulicher, besser verständlich
⇒ Fortfahren mit den gerundeten Werten
Dreidimensionale Erweiterung der Gefahrenfunktion
[Bearbeiten]- Für eine dreidimensionale Funktion muss Argument um die y-Variable erweitert werden
- Daraus folgt für die beiden oben ermittelten Funktionen:
und
- Annahme: Windrichtung in positive Richtung
- Für verschiedene Windrichtungen (siehe Zyklus II) erhält man eine Darstellung in Abhängigkeit des Winkels α:
.
- Windrichtung: α in Bogenmaß von [0,2π]
- Es gilt wieder für die Gesamtfunktion:
Berücksichtigung der zeitlichen Komponente
[Bearbeiten]- Berücksichtigung des radioaktiven Zerfalls: Multiplizieren des Zählers, der einer radioaktiven Belastung entspricht mit einer exponentiellen Zerfallsfunktion
- : Zerfallskonstante des jeweiligen Atoms.
- Betrachte (analog zu Zyklus 1) Cs-137 mit einer Halbwertszeit ca. 30 Jahren:
Damit:
- Der Gefahrenwert hängt somit von den vier Eingabewerten ab.
Computergestützte Umsetzung mit Geogebra und Maxima
[Bearbeiten]Geogebra
[Bearbeiten]- Die Funktionen können sowohl im 2- als auch im 3-dimensionalen mit Hilfe von Geogebra visualisiert werden
- Mit Hilfe von Schiebereglern: Variation der Windrichtung und der Zeit ⇒ Dynamische Veranschaulichung der Abhängigkeiten und Zusammenhänge

Maxima
[Bearbeiten]- Funktionen im 3-dimensionalen mit Gitternetzlinien dargestellt (Vereinfachung der 3-dimensionalen Wahrnehmung)
- Ausgabevariable je nach Betrag farbig dargestellt
- Festlegung auf eine Zeit und eine Windrichtung ⇒ Bezug auf die Funktionen, die weder die Zeitabhängigkeit noch die Windrichtung berücksichtigen:
f(x,y):=(1480)/(1+(7/10000)*(x^2+y^2)); g(x,y):=(40)/(1+(1/7500)*((x-1080)^2+(y)^2)); u(x,y):= f(x,y)+g(x,y);
Graphische Darstellung
[Bearbeiten]Um die Funktion graphisch darzustellen wird der Code wxplot3d verwendet:
wxplot3d(u(x,y),[x,-100,1300],[y,-1000,1000],[grid,100,100]); (Alternativ wxplot3d(f(x,y)+g(x,y),[x,-100,1300],[y,-1000,1000],[grid,100,100]); )
- Erste Eingabe: Definition der zu plottenden Funktion
- Zweite und Dritte Eingabe: Definition der Variablen und der Bereiche, in denen die Funktion ausgewertet werden soll
- [grid,100,100] : Feldlinien, entlang derer die Funktion ausgewertet wird, werden enger dargestellt, wodurch der Graph im Gesamten stetiger aussieht
Graph
[Bearbeiten]
Exaktere Endfunktion mit Maxima
[Bearbeiten]- Koeffizienten der Funktion werden durch ein nicht-lineares Gleichungssystem gelöst
- Parameter des Gleichungssystems werden in Maxima ausgelesen
- Erstellung der exakten Endfunktion
- Plot der exakten Endfunktion
Maxima Code zur Erstellung der exakteren Funktion
[Bearbeiten]gl1: 1480=a1/(1+b1*(0^2))+a2/(1+b2*(0-1080)^2); gl2: 185=a1/(1+b1*(100^2))+a2/(1+b2*(100-1080)^2); gl3: 10=a1/(1+b1*(930^2))+a2/(1+b2*(930-1080)^2); gl4: 40=a1/(1+b1*(1080^2))+a2/(1+b2*(1080-1080)^2); GS: solve([gl1,gl2,gl3,gl4],[a1,a2,b1,b2]); a1: rhs(GS[4][1]); a2: rhs(GS[4][2]); b1: rhs(GS[4][3]); b2: rhs(GS[4][4]); u(x):=(a1)/(1+(b1)*(x^2+y^2))+(a2)/(1+b2*((x-1080)^2+(y)^2));
Maxima Code für den Plot der exakteren Funktion
[Bearbeiten]- Zusätzliche Farbanpassung des Graphen, sodass auch kleinere Veränderungen der Risikowerte farblich stärker hervorgehoben werden:
plot3d(u(x),[x,-400,1300],[y,-500,500],[z,0,700],[grid,80,80], [zlabel, "Risiko"],[palette, [gradient, yellow, green, cyan, cyan, blue, blue, blue, magenta, magenta, magenta, magenta, red, red, red, red, red]]);

Resultate der Modellierung
[Bearbeiten]- Endresultat: Darstellung einer Gefahrenfunktion , die das zeitliche und räumliche Gefahrenpotential eines Nuklearunfalls unter Berücksichtigung eines nuklearen Wash-Outs beschreibt
- In Geogebra: Visualisierung des Risikos in Windabhängigkeit und im zeitlichen Verlauf nach der Katastrophe
Resultate Graph
[Bearbeiten]- Am oben gezeigten Graphen wird das Risiko deutlich visualisiert
- Globales Maximum am Ort des Kraftwerks
- Hohes Risiko in seiner Umgebung
- Im Vergleich wirkt das lokale Maximum des Risikos sowie in dessen umliegenden Bereich (in dem es zum nuklearen Fallout kommt) vernachlässigbar klein ⇒ Jedoch in der Realität keinesfalls vernachlässigbar
Interpretation
[Bearbeiten]- Menge an radioaktiver Belastung und dem damit verknüpften Risiko kann (siehe Zyklus 1 sowie Auswirkungen von Tschernobyl) noch jahrzehntelang zu gesundheitlichen Gefahren führen
- Belastung im Umfeld des Kernkraftwerks so groß, dass die Radioaktivität Menschen nicht durch Mutationen langfristig schadet, sondern unmittelbar nach dem Unglück innerhalb weniger Minuten oder Stunden töten kann
Resultate in Realsituation
[Bearbeiten]- Kaum Aussagen über allgemeinere Resultate möglich ⇒ Bis heute nur zwei größere Reaktorunfälle
- Die Modellierung selbst stützt sich auf Daten von Tschernobyl und modelliert die dortige Situation entsprechend adäquat
- Die Anwendbarkeit auf Fukushima problematisch
- Kein nuklearer Fallout aufgrund von radioaktivem Niederschlag über dem Festland
- Nach den ersten Tagen kam es in Japan auch vereinzelt zu radioaktivem Niederschlag, jedoch kann man nicht von einer annähernd konstanten Windrichtung ausgehen, da Zyklone Ursache des Windes
- Windabhängigkeit wissenschaftlich definitiv bestätigt
Bewertung und Optimierung
[Bearbeiten]Bewertung
[Bearbeiten]- Dieser Modellierungszyklus verbindet mit einer Funktion die zeitlichen und die räumlichen Risiken nach einer Nuklearkatastrophe
- Anhand des Graphen entsteht der Eindruck, dass das Risiko nur in Nähe des Reaktors besonders hoch ist ( Risikowert um ein Vielfaches höher als überall sonst), insbesondere auch am Ort des Niederschlags
Bezug zur Realität
[Bearbeiten]- Strahlenbelastung im Gebiet so groß, dass Sperrzonen gebildet werden müssen (Grund: kurzer Aufenthalt in risikoreichen Gebieten kann zum Tod führen)
- Enorme Belastung am Kraftwerk hat eine Skalierung zur Folge, die nicht mit den Vorstellungen und Gegebenheiten der vergangenen Katastrophen übereinstimmt
- Maximum am Ort des Niederschlags erklärt warum beispielsweise Rotwild in Südbayern bis heute aufgrund der Strahlenbelastung nicht gegessen werden kann
- Hohe Komplexität der Zerfallsprozesse und der Verbreitung von Stoffen
Optimierung
[Bearbeiten]- Beachtung wechselnder Luftströmungen bzw. Windrichtungen und verschiedener Windstärken (s. Infografik dpa: mehrerer in Europa verteilter Gebiet mit höherer Kontamination)
- Diffussionsprozesse in der Luft, wodurch die Ausbreitung der radioaktiven Wolke modelliert werden kann
- Herabsinken der Nuklide aufgrund der Gravitation wird nicht berücksichtigt:
- Realsituation: Gebiet in Windrichtung würde ebenfalls stärkere radioaktive Belastung aufzeigen
- Zeitlicher Einfluss aller Nuklide, nicht nur Cs-137
Siehe auch
[Bearbeiten]
Seiteninformation
[Bearbeiten]Diese Lernressource können Sie als Wiki2Reveal-Foliensatz darstellen.
Wiki2Reveal
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Mathematische Modellbildung' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Mathematische%20Modellbildung/Themen/Radioaktivit%C3%A4t%20und%20Risikoliteralit%C3%A4t/Modellierungszyklen
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.











































































