Kurs:Räumliche Modellbildung/Gruppe 13
Gruppenseite - (KSS)
[Bearbeiten]Diese Seite enthält die gesammelten Materialien der Gruppe 13 für die Portfolioprüfung.
Teilnehmer
[Bearbeiten]- Kolb, David
- Schumacher, Eric
- Stassek, Fabian
Diskrete Modellierung
[Bearbeiten]Modellierung Transportmatrix und Impfungen mit Excle (10.06.2021)
[Bearbeiten]Zyklus 1
[Bearbeiten]Im folgenden Modell betrachten wir uns 1000 Personen, die wir auf 5 verschiedene Orte aufteilen wollen. Am ersten Ort sind 400 Personen, am zweiten Ort 170 Personen, am dritten Ort 120 Personen, am vierten Ort 90 Personen und am fünften Ort 220 Personen. Da wir uns in der diskreten Modellbildung befinden, stellen wir uns anschaulich vor, dass die 5 Orte verschiedene Flughäfen repräsentieren, die man über Direktflüge miteinander verbinden kann. So fliegen bspw. 20% der Personen von Flughafen A zu Flughafen B und die anderen 80% zu Flughafen E. Eine solche Umverteilung der Personen erstellen wir für jeden Flughafen und wollen uns dies zunächst modellhaft darstellen. Dabei ist zu beachten, dass nicht alle Flughäfen direkt miteinander verbunden sind und dass es auch möglich ist, dass Personen an einem Flughafen festsitzen und sich nicht fortbewegen. Die eckigen Kästen stellen unsere Flughäfen da und die Zahlen in den Pfeilen zeigen an, wie viel Prozent der Personen von Flughafen X zu Flughafen Y fliegen.

Im nächsten Schritt wollen wir das Modell mathematisch auffassen. Dazu schreiben wir unser Modell in eine 5x5-Matrix um. Diese wird von oben nach unten gelesen und gibt uns die Beförderungsdaten von dem obigen Modell wieder. Die Anzahl der Personen an den verschiedenen Flughäfen schreiben wir in einen Spaltenvektor um. Mit dem Tabellenkalkulationsprogramm MS Excel können uns wir so durch einfache Matrizen-Multiplikation (=MMULT) die Anzahl der Personen in einem neuen Zeitschritt anzeigen lassen. Wir erhalten erneut einen Spaltenvektor (Transport 1) und können ablesen, wie viele Personen sich nun wo befinden.

Bemerkung
[Bearbeiten]Im Rahmenplan Mathematik des Landes Rheinland-Pfalz sind Matrizen in den Wahlpflichtgebieten der gymnasialen Oberstufe aufgelistet. Im Grundfach gibt es den Unterpunkt "Matrizen in der praktischen Anwendung". Hier wäre eine solche Modellierung durchaus denkbar und praxisnah anwendbar.
Zyklus 2
[Bearbeiten]Jetzt wollen wir einen Schritt weiter gehen und betrachten uns zusätzlich die epidemiologischen Prozesse, die innerhalb eines Flughafens vonstattengehen. Wir unterteilen die Personen an den Flughäfen in empfängliche Personen (S), infizierte Personen (I) und bereits genesene Personen (R). An den Flughäfen stecken sich 20% der dort anwesenden Personen mit einer Krankheit an. Die Hälfte der Infizierten verharrt weiter in diesem Stadium, während die andere Hälfte in die Gruppe der Genesenen wechselt. Vollständig genesene Personen sollen künftig immun gegen die Krankheit bleiben. Anhand dieser neuen Daten wollen wir uns obiges Transportmodell durch die Hinzunahme der epidemiologischen Prozesse erweitern.
Nun wollen wir auch das erweiterte Modell mathematisch auffassen und schreiben analog zum ersten Zyklus das SIR-Modell in eine 3x3-Matrix um.

Die Ausgangssituation im Zeitpunkt t=0 soll folgendermaßen aussehen:
- Flughafen A: 100 Empfängliche / 200 Infizierte / 100 Genesene
- Flughafen B: 020 Empfängliche / 060 Infizierte / 090 Genesene
- Flughafen C: 120 Empfängliche / 000 Infizierte / 000 Genesene
- Flughafen D: 030 Empfängliche / 030 Infizierte / 030 Genesene
- Flughafen E: 050 Empfängliche / 040 Infizierte / 130 Genesene
Auch diese Aufteilung übertragen wir von unserem Modell in eine 5x3-Matrix. Insgesamt erhalten wir eine ständige Hintereinander-Ausführung von Matrizen Multiplikationen. Zunächst erfolgt ein Transport der Personen (aufgeteilt in S, I und R) von Flughafen X zu Y. Dazu multiplizieren wir, wie in Zyklus 1 dargestellt, die Transportmatrix (gelb) mit der 5x3-SIR-Matrix. Anschließend kommt es am Flughafen zu epidemiologischen Prozessen. Dazu multiplizieren wir die neue SIR-Matrix mit der Infektionsmatrix (blau). Die Personen fliegen wieder weiter und die Multiplikation mit der Transportmatrix kommt erneut zum Tragen. Der Zyklus beginnt von vorne.

Zyklus 3: Implementierung in Octave und Plotten der Ergebnisse
[Bearbeiten]Das bisherige Excle-Modell soll nun mithilfe von Octave in weiteren Schritten optimiert werden.

Sie sehen hier das Endresultat unserer Modellierung. Im Folgenden wird der Entstehungsprozess schrittweise aufgezeigt.
Fragestellungen:
- Wie wirkt sich der Transportprozess auf den epidemiologischen Verlauf aus?
- Reicht es aus, wenn wir ein Gebiet durchimpfen, um global die Epedemie aufzuhalten?
Ausgangssituation
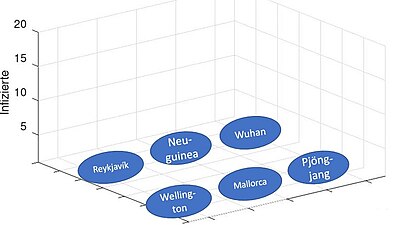
[Bearbeiten]Wir definieren uns 6 Orte (Hauptsächlich Inseln, auf denen Infektionen hauptsächlich durch den Lufttransport "eingeschleppt" werden können) Angegeben werden dazu die SIR-Zahlen. Zu Beginn gibt es lediglich in Wuhan Infizierte, die andern Orte sind "Coronafrei".
Die Verteilung in t=0 sieht folgendermaßen aus:
| Ort | S | I | R |
|---|---|---|---|
| Wuhan | 100.000 | 100 | 0 |
| Neuguiena | 90.000 | 0 | 0 |
| Reykjavik | 120.000 | 0 | 0 |
| Wellington | 60.000 | 0 | 0 |
| Mallorca | 110.900 | 0 | 0 |
| Pjöngjang | 100.000 | 0 | 0 |
Diese Orte stehen durch einen Flugnetz in gegenseitiger Beziehung. Dadurch kann sich nun die Krankehit auch in anderen Orten verbreiten. Wir starten mit 100 Infizierten in Wuhan.

Code in Octave
[Bearbeiten]Die Verteilung der Orte inkl. SIR wird in einer 6x3-Matrix B gespeichert.

Die diagonaldominante Transportmatrix sieht dabei wiefolgt aus:

(Achtung: Die TransportMatrix wird enorm groß, wennn wir mehrere Orte betrachten. Angenommen wir nehmen eine Landkarte, Teilen diese in 5x5 Quadrate. Dann ist die dazugehörtige TransportMatrix eine 25x25 Matrix (bereits 625 Einträge)
Nun werden weitere Parameter definiert, die zur Modellierung benötigt werden:
- Infektionsgeschwindigkeit=0.0000035
- Genesungsrate=1/10
- Wochen=15
Wir wollen nachher unsere Coronainfizierten in 3D plotten. Auf der Y-X-Ebene liegen dabei unsere 6 Orte. Die Z-Achse gibt die Anzahl der Infizierten an. Dazu müssen die 6 Orte zunächst an ihre jeweiligen Orten definiert werden (oben). Dann plotten wir die Ausgangssituation in t=0 der Daten aus der Matrix B (unten).

Nun muss der Infektionsprozess stattffinden. Dieser soll 7 Mal durchlaufen werden. Danach: -> Transport findet statt, bei dem auch Infizierte in neue Gebiete erstmalig gelangen. Dann verbreitet sich die Krankheit wieder 7 Tage, bis der nächste Flugtransport stattfindet. Vorgang wird beliebig oft wiederholt.(7 Tage Infektion, anschließend 1 Transportprozess: dies wird im Code durch eine verschachtelte forschleife berechnet).
Für den Infektionsprozess darzustellen wird eine neue Matrix B mit 3 Spalten definiert. Sie wird iefolgt aufgebaut: (nach dem Vorgehen [S|I|R])
B = [B(:,1) - B(:,2) .* B(:,1) * Infektionsgeschwindigkeit | B(:,2) + B(:,2) .* B(:,1) * Infektionsgeschwindigkeit -B (:,2) * Genesungsrate | B(:,3) + B(:,2) * Genesungsrate]
Nachdem dieser Prozess 7 Mal stattgefunden hatte, wird der Transportprozess 1. Mal ausgeführt.
Für den Transport zu berechnen überschreibt eine neue Matrix B die alte, die folgendermaßen definiert wird:
B=TransportMatrix*B
Dabei ist das rechte B jenes nach dem zuletzt durchgeführen Infektionsprozess.
Nun können wir den gesammten Prozess wiederholen, wir haben uns auf 15x geeinigt wodurch über 100 Tage simuliert werden. Die einzelnen Bilder werden gespeichert und zu einer GIF-Datei zusammengesetzt.
klassisches SIR-Modell mit Transportmatrix
[Bearbeiten]Aus dem gerade beschriebenen Code ergibt sich folgende Annimation. Zusätzlich werden unten zu dem jeweiligen Ort die Empfänglichen abgebildet:
- Die Infektion wird von Wuhan nach und nach in die übrigen Orte transportiert und verbreitet sich dort
- Es ergibt sich der klassische SIR-Verlauf in jedem Ort
- nach Pjöngjang gelangt kein Infizierter, da wir diese Stadt realitätsnah isoliert von der restlichen Welt gelegt hatten. Somit kann sich Corona nie ausbreiten und alle Menschen bleiben Empfänglich.
Veranschaulichung des Transportprozesses
Um zu zeigen, wie und wann Infizierte in den anderen Orten entstehen werden die ersten 20 Tage in Zeitlupe wieder geplottet. Dabei wird auch die Z-Achsen-Skallierung angepasst.

+ Impfung in einem Ort
[Bearbeiten]Nun wollen wir Impfungen in unser Modell miteinfließen lassen. Dazu wird eine Impfmatrix definiert, welche in jedem Zeitschritt der Matrix B abgezogen wird. Durch diese Rechnung wandern in jedem Zeitschritt Personen von der Gruppe S zu der Gruppe G, ohne den "Zwischenweg" der Infektion zu gehen.
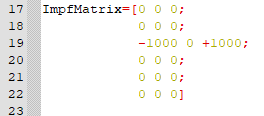
In diesem Fall werden nur in Rekjavik Impfungen verabreicht, die übrigen Orte gehen leer aus.
Die ImpfMatrix wird im Code folgendermaßen eingebaut:
B = [B(:,1) - B(:,2) .* B(:,1) * Infektionsgeschwindigkeit | B(:,2) + B(:,2) .* B(:,1) * Infektionsgeschwindigkeit -B (:,2) * Genesungsrate | B(:,3) + B(:,2) * Genesungsrate] + ImpfMatrix
Kurzer Exkurs

Diese Modellierung bezogen auf die aktuelle Impf-Situation: Man könnte die Frage stellen, ob eine große Impfbevölkerung in Europa/ Nordamerika ausreichen würde, die Pandemie Weltweit besiegen zu können. So ähnlich ist die Situation aktuell. Siehe Grafik rechts. (Quelle wdr.de)
Aus der Modellierung kann man den Schluss ziehen, dass eine hohe Impfrate auf einem Kontinent global wenig bewirkt für die anderen Kontinente. Man müsste weltweit genügend Impfstoff zur verfügung stellen, um die Ausbreitung effektiv bremsen zu können, siehe folgende Modellierung im nächsten Schritt.
+ Impfung überall (unterschiedliche Impfmenge)
[Bearbeiten]Neue ImpfMatrix wurde definiert, die alle Orte mit Impfungen versorgt. Prozess wird wieder dargestellt.

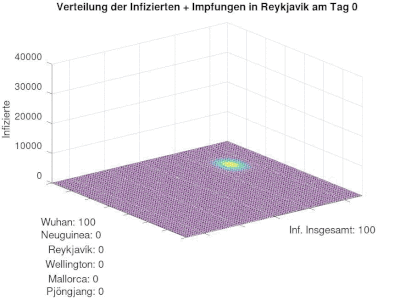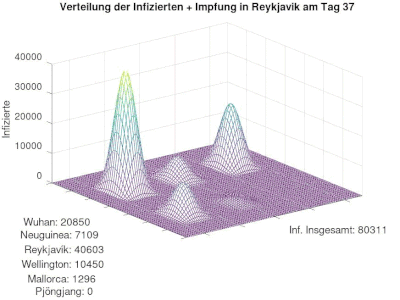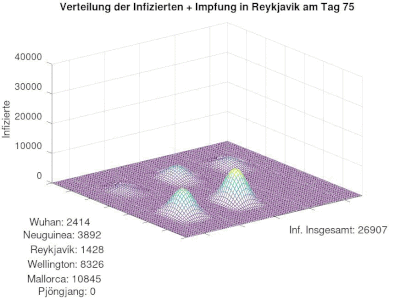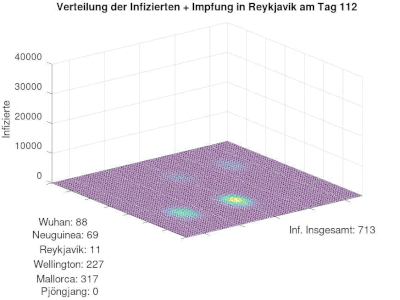


.
+ regionaler, veränderlicher Infektionsrate
[Bearbeiten]Kritikpunkt der bisherigen Simulation ist, dass die tatsächlichen Infektionsverläufe nicht nach dem klassischen SIR-Modell verlaufen. Eine Pandemie läuft in Wellen. Mal verbreitet sich die Infektion schneller oder langsamer, das Wetter hat seinen Einfluss und Lockdowns und Öffnungen wirken sich auf den Verlauf aus. Diese Einwirkungen sind jedoch auch in jedem Ort verschieden, wodurch zu jedem Ort eine individuelle Infektionsrate definiert werden muss. Dies geschieht, indem die Infektionsraten in einem Spaltenvektor (1x6) gespeichert werden.
![]()
Der sonstige Code bleibt dabei uverändert. Lediglich werden mehrmals die Werte des Vektor angepasst, sodass der typische Wellenverlauf entsteht.
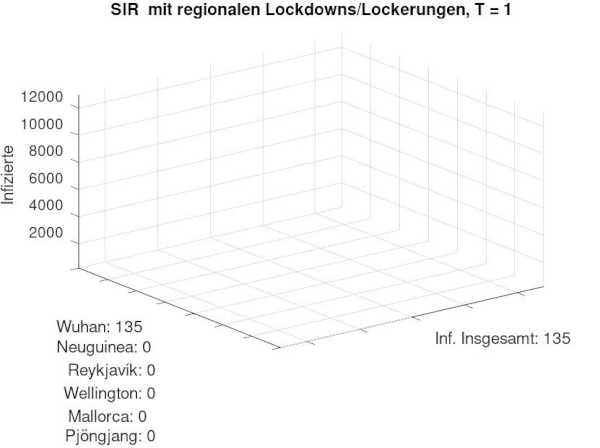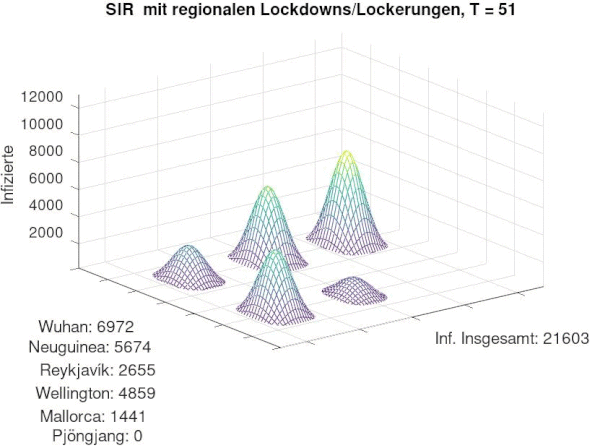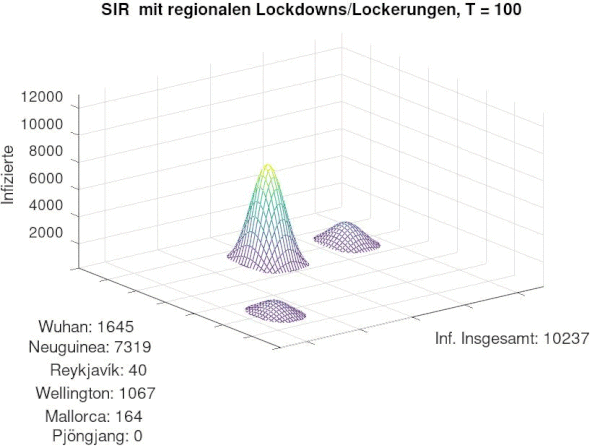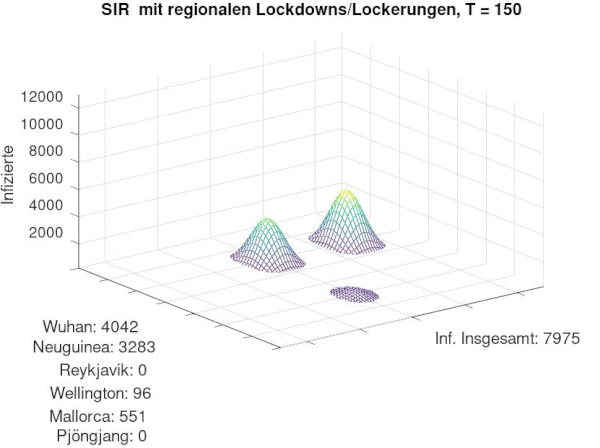
.
+ regionaler, veränderlicher Infektionsrate + Impfungen ab Tag 50
[Bearbeiten]Die ersten 50 Tage laufen exakt identisch. Dann wird an allen Orten täglich mehr oder wenig viel geimpft. Die Infektionsraten bleiben dabei gleich.
letzte Verfeinerung
[Bearbeiten]Zunächst haben wir uns angeschaut, wo unsere 6 Städte auf der Welt verteilt liegen. Dann haben wir diese Weltkarte in unsere Simulation "eingeführt" und die Städte im Code in der entsprechenden Matrix an ihre richtigen Koordinaten gesetzt. Auf die XY-Ebene ist dadurch eine Weltkarte angedeutet, sodass die Orte einfacher zugeordnet werden können.


Nun betrachten wir uns an den jeweiligen Orten die SIR Gruppen.

Als Ergebniss erhalten wir nun eine 3-D Annimation. Wenn wir nun nicht nur unsere 6 Orte betrachten würden, sondern alle Städte der Welt, würde eine 3-D Annimation entstehen, die das Infektionsgeschehen auf der ganzen Welt abbilden könnte.
SIR-Modell
[Bearbeiten]Was ist das SIR Modell und was kann es?
[Bearbeiten]Das SIR-Modell (susceptible-infected-removed) veranschaulicht in der mathematischen Epidemiologie die Ausbreitung von ansteckenden Krankheiten innerhalb einer Bevölkerung. Die gesamte Bevölkerung lässt sich dabei in die drei Gruppen empfängliche Personen (S), aktuell Infizierte (I) und bereits genesene/ gestorbene (R) einteilen. Man kann sich diese drei Gruppen wie drei Töpfe vorstellen und zu jedem Zeitpunkt des Geschehens kann jeder Einzelner dabei genau einem dieser Töpfe zugeordnet werden.
Bevor eine neue Krankheit zum ersten Mal ausbricht, befindet sich die gesamte, immunologisch naive Bevölkerung im Topf der empfänglichen Personen. Infiziert sich nun die erste Person, "wandert" dieser vom Topf S zu I. Alle weiteren Personen, die sich danach anstecken folgen ihm in diese Gruppe. Hier verbleiben sie so lange, bis sie nicht mehr ansteckend bzw. genesen sind und werden schließlich dem Topf R zugeornet.
Die Anzahl der empfänglichen Personen (S) wird dabei bis zum Zeitpunkt der letzten Ansteckung immer kleiner. Würde sich die gesamte Bevölkerung irgenwann infizieren, wäre der komplette Topf leer. Die Anzahl der genesenen (R) steigt so lange, bis kein "Nachschub" aus dem Top I mehr kommt. Dies würde dann der Fall sein, wenn sich niemand mehr ansteckt und der letzte Infizierte wieder gesund ist.
Die Anzahl von S+I+R ist im gesamten Prozess konstant und gibt die Größe der betrachteten Bevölkerung an.
Kritik
[Bearbeiten]In diesem Modell wird das Infektionsgeschehen stark vereinfacht dargestellt. Fehlerhaft ist dabei folgendes:
- die Bevölkerung ist immer gleich groß, Geburten,Tote Zu- und Auswanderung werden nicht berücksichtigt
- alle Menschen werden gleich betrachtet, es gibt keine Superspeader und niemand hat ein höheres/ niedrigeres Risiko einer Infektion
- alle Infizierten werden danach immun und sind nicht mehr empfänglich
- Impfungen und die Inkubationszeit werden außer Acht gelassen
- die räumliche Verbreitung fehlt völlig
- Maßnahmen des Infektionsschutzes können schwer veranschaulicht dargestellt werden
- Fehlende Altersstrucktur
Dennoch hat das SIR seine Berechtigung, denn es vereinfacht als Modell die Darstellung der Realität und bietet somit eine Grundlage für weitere, optimierte Modellierungsansätze.
Optimierung
[Bearbeiten]Im Folgendem ist eine eigenerstellte optimierte Version des SIR-Modells abgebildet. Es wurde versucht, auf möglichst viele obenstehende Kritikpunkte einzugehen.

Weitere Optimierungsmöglichkeiten:
- Unterscheidung zwischen Erst- und Zweiimpfung und keine direkte Immunität nach Impfung (2 Wochen Dauer)
- Untergliederung der Bevölkerung in Altersgruppen
- Optimierung der Impfungen: Betrachtung der verschiedenen Impfstoffe und ihrer Wirksamkeit in Abhängigkeit von der verabreichten Dosis (1./2. Impfung)
Einführung unseres Modells (Herxheim 2020)
[Bearbeiten]Das eigen erstelle Modell finden Sie zur besseren Übersichtlichkeit auf folgender Verlinkung Herxheimer Modell
2.0
Sport und Mathematik im Kletterpark
Kontinuierliche Modellierung
[Bearbeiten]Tutorium 1 - Kontaktmodell
[Bearbeiten]
Die erste Tutoriumsaufgabe beschäftigt sich mit dem Kontaktmodell. Dabei soll die räumliche Ausbreitung einer Infektion in einem gewissen Zeitabschnitt vereinfacht dargestellt werden (siehe Animation auf der rechten Seite). Dabei ist unsere Gruppe in folgender Reihenfolge vorgegangen: Zunächst haben wir uns ein Modell betrachtet, bei dem es noch keinen Infizierten gab und der Fokus zunächst auf den Zusammenhang der verschiedenen Parametern Bewegungsgeschwindigkeit, Zeiteinheiten, ... etc. lag. In einem zweiten Modell wurde nun ein Infizierter mit in die Simulation aufgenommen. Dessen Standort wurde je ein Mal in die Mitte und ein Mal in eine Ecke der Bevölkerung festgelegt. In einem dritten Durchgang wurde unterschieliche Ansteckungsradien simuliert und deren Einfluss auf die Anzahl der Infektionen. Im letzten Modell wurde schließlich das Skript so bearbeitet, dass sich die Bewegungsrichtung der Passanten nach gewissen Zeitschritten zufällig verändert hat.
Theorie des deterministischen Kontaktmodells
[Bearbeiten]Unterschreitet ein Individuum einen vorgegebenen Abstand zu einem infizierten Individuum, so wird Ersteres infiziert. Der Abstand der einzelnen Individuum zueinander kann dabei in einem metrischem Raum beispielsweise durch den Satz des Pythagoras bestimmt werden. Eine Abbildung auf eine Menge der Individuen , die jeder Person ihren epidemiologischen Status zuordnet, kann dabei wie folgt definiert werden.
Eine Infektion findet innerhalb des deterministischen Kontaktmodells wie folgt statt: Unterschreitet ein infiziertes Individuum zu einem anfälligen Individuum , wobei , das als Kontaktdistanzschranke, dann infiziert die Person .
Der Bearbeitung der Tutoriumsaufgabe liegt dabei die Annahme zugrunde, dass sich die Individuen (Passanten) mit einer konstanten Geschwindigkeit in eine zufällige Richtung bewegen. Nähert sich ein anfälliger Passant einer infizierten Person nah genug, so wird dieser sofort infiziert.
a) Modell ohne Infizierten
[Bearbeiten]Zu beginn basteln wir uns eine kleine Bevölkerung (400 Personen, grüne Sternchen), die zu einem Starzeitpunkt t=0 gleichmäßig mit einem Abstand von 1 im Raum verteilt sind. Die Individuen bewegen sich mit fotlaufender Zeit in eine bestimmte Richtung (zufällig aber fest). In unserem ersten Modell befinden sich ausschließlich gesunde Personen.
Nx=20;
Ny=20;
x=[1:Nx];
y=[1:Ny];
%Erzeugen eines Punktegitters
[x,y]=meshgrid (x,y);
Die Personen bewegen sich nun zufällig im Raum
%Definition der Bewegungsgeschwindigkeit g=1; %Definition der Zeiteinheit T=6; %Anzahl der Zeitschritte Zeitschritte=2; dt=1/Zeitschritte*T; %folgender Zielpunkt soll am Ende erreicht werden: neuPosX=x.+g.*rand(Ny,Nx)-0.5; neuPosY=y.+g*rand(Ny,Nx)-0.5; %im Folgenden werden die benötigten einzelnen Zwischenschritte berechnet, um den Zielpunkt zu erreichen %der Index i läuft dabei von 0 bis 12 (Zeitschritte*T) for i=0:T*Zeitschritte neuX=x.+(neuPosX.-x)*i*dt; neuY=y.+(neuPosY.-y)*i*dt;
Fazit & Optimierungsmöglichkeiten
Die einzelnen Menschen bewegen sich zufällig (aber fest) in unserem ersten Modell. In einer Bevölkerung ohne Infizierten kann sich natürlich auch keine Krankheit ausbreiten. Dies wollen wir nun in Modell b) ändern.
b) Modell mit einem Infizierten
[Bearbeiten]Um eine Ausbreitung einer Krankheit modellieren zu können, brauchen wir einen Anfangsinfizierten. Dabei ist es für die Ausbreitung der Krankheit wichtig, wo sich der erste Infizierte zu Beginn befindet. Daher betrachten wir im Folgenden zwei verschiedene Varianten (Zentrum und Ecke). Sobald der Abstand einer gesunden Person zu einer infizierten Person kleiner als 0.8 ist, überträgt sich die Krankheit. Infizierte Personen sollen mit einem roten Quadrat gekennzeichnet werden.
Der Anfang ist identisch zu Modell a). Zusätzlich wird eine infizierte Person in die Mitte definiert
%Infizierte Person befindet sich im Mittelpunkt der Bevölkerung xInf=x(1,Nx/2); yInf=y(Ny/2); IndInf2=Nx/2; IndInf1=Ny/2; IndInf1neu=IndInf1; IndInf2neu=IndInf2; %Der Ansteckungsradius beträgt 0.8 radiusInf=0.8;
Definition der Ausgangslage mit einem Infizierten
figure (20)
hold on;
plot(x , y, '*g')
plot(xInf,yInf,'sr')
axis([-2 22 -2 22])
title('Startposition')
hold off;
Anzahl=0
Definition einer Schleife für die einzelnen Zeitschritte
%Für jeden Zeitschritt soll die Position der einzelnen Punkte festgehalten werden
for i=1:T*Zeitschritte
neuX=x.+1*(neuPosX.-x)*i*dt;
neuY=y.+1*(neuPosY.-y)*i*dt;
figure (i+1000)
title(['t=' num2str(i*dt)])
axis([-2 22 -2 22]);
hold on;
Die Infizierten werden mit einem roten Quadrad umrandet. Für jede Person und für jeden Zeitschritt wird der Abstand zu den Infizierten gemessen. Ist der Mindestabstand unterschritten, gilt die Person auch als infiziert. Anschließend wird noch abgeglichen, ob die neu-infizierte Person nicht vorher schon infiziert war. Ist dies der Fall wird die Person nicht als Neuinfektion gewertet, um eine doppelte Zählung zu verhindern.
plot(neuX,neuY,'*g');
zahler=1;
for k1=1:length(IndInf1)
for j=1:Nx
for l=1:Ny
abstand=norm ( [neuX(l,j)-neuX(IndInf1(k1),IndInf2(k1)), neuY(l,j)-neuY(IndInf1(k1),IndInf2(k1))]);
if abstand<radiusInf
abstand;
plot(neuX(l,j),neuY(l,j), '*r') ;
%---------------------------
k2=1;
while k2 <=length(IndInf1)&&(l!=IndInf1neu(k2) || j!=IndInf2neu(k2))
k2=k2+1;
endwhile
if k2 >length(IndInf1)
IndInf1neu=[IndInf1neu l];
IndInf2neu=[IndInf2neu j];
endif
endif
endfor
endfor
endfor
IndInf1=IndInf1neu;
IndInf2=IndInf2neu;
hold off
%Die Bilder der einzelnen Schritte werden gespeichert
%Lauftext=["Fig_", num2str(i+1000), ".jpg"]
%saveas((i+1000), Lauftext)
%Die Anzahl der Infizierten werden noch für jeden Zeitschritt gezählt
lengt=length(IndInf1)
Anzahl= [Anzahl lengt];
endfor
-
Erstinfektion am Rand der Gesellschaft
-
Erstinfektion in der Mitte der Gesellschaft
Fazit & Optimierungsmöglichkeiten
Die einzelnen Menschen bewegen sich wieder zufällig (und fest). Zum Vergleich haben wir den Anfangsinfizierten einmal in die Mitte gesetzt und einmal in die Ecke. Dabei kann man erkennen, dass die Ansteckungszahlen je nach Ausgangslage unterschiedlich ist. Eine Krankheit, die am "Rand der Gesellschaft" ihren Ursprung hat, wird sich dementsprechend (wie es auch in den Animation dargestellt wird) zu Beginn langsamer ausbreiten, als eine Krankheit, die ihren Ursprung "im Mittelpunkt der Gesellschaft" hat. Bisher haben wir verschiedenen Ausgangslagen betrachtet und wollen uns nun unterschiedlichen Ansteckungsradien widmen. Dies kann man beispielsweise durch das Tragen einer Schutzmasken in der Corona-Pandemie vergleichen.
c) Modell mit unterschiedlichen Ansteckungssradien
[Bearbeiten]In diesem Modell verändern wir den Radius. Man kann sich das so vorstellen: Wenn der Radius größer wird, liegt beispielsweise eine neue Virusmutante vor, die sich leichter (über eine größere Distanz) verbreitet. Wenn der Radius kleiner wird könnte das bedeuten, alle Menschen tragen schützende FFP2 Masken. Somit muss ein engerer Kontakt bestehen, um sich überhaupt infizieren zu können. Das Skript bleibt das gleiche wie in Modell b). Einzig der Ansteckungsradius wird hier verändert. Im 1. Durchlauf benutzen wir einen Ansteckungsradius von lediglich 0.3. Somit müssten sich die Menschen viel näher kommen um sich anzustecken. Dies könnte durch konsequentes Nutzen von FFP2 Masken resultieren oder eine ungefährlichere Virusvariante (linkes Bild) Im 2. Durchlauf wird der Ansteckungsradius auf 1.1 heraufgestuft. Eine Infizierung wird somit viel wahrscheinlicher, da der Mindestabstand nicht eingehalten werden kann. Dies könnte mit einer aggressiveren Virusvariante einhergehen (rechtes Bild)
Vergleich der Endpositionen je nach Ansteckungsradius
In der folgenden Bildergalerie wurden die Endpositionen je nach Ansteckungsradius illustriert. Das erste Bild stammt aus Modell b) und der gewählte Radius beträgt dabei 0.8. Das Bild in der Mitte zeigt die Endposition mit einem Radius von 0.3. Es wird deutlich, dass sich am Ende weniger Menschen angesteckt haben als bei der ursprünglichen Variante. Einen deutlichen Infektionsanstieg zeigt das Bild auf der rechten Seite. Hier ist der Ansteckungsradius bei 1.1, was man mit einer aggressiven Virusvariante vergleichen könnte. Insgesamt zeigt sich also je nach Ansteckungsradius eine unterschiedlich hohe Infektionszahl (verglichen im selben Zeitraum).
-
Endposition bei ursprünglicher Variante (Radius=0.8)
-
Endposition beim Tragen einer FFP2 Maske (Radius=0.3)
-
Endposition bei aggressiver Virusvariante (Radius=1.1)
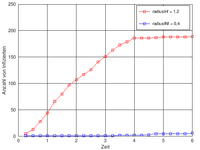
Fazit & Optimierungsmöglichkeiten
Wie eben bereits beschrieben erhalten wir je nach Ansteckungsradius eine andere Infektionslage. Als Optimierungsmöglichkeit wäre hier sicherlich den Radius der aggressiven Virusvariante unter 1.0 zu setzen, da sich sonst bereits im ersten Zeitschritt alle Personen die um Umfeld des Anfangsinfizierten sind mit der Krankheit anstecken. Nun wurden in den Modellen b) und c) die Infektionslage je nach Lage des Erstinfizierten und den verschiedenen Ansteckungsradien betrachtet. Die Bewegung wurde dabei immer zufällig, aber fest gewählt. Dies soll in einem letzten Modell d) verändert werden
d) Modell mit Änderungen in der Bewegungsrichtung
[Bearbeiten]In einem letzten Modell soll nun die Bewegungsrichtung der einzelnen Punkte nach gewissen Zeiteinheiten verändert werden. Dabei gehen wir zunächst wie in den bisherigen Modellen vor und verweisen auf das Skript in Modell b). Die erste Schleife wird also genau so ausgeführt. Einziger Unterschied besteht darin, dass Infizierte dieses Mal rot eingefärbt und nicht mit einem roten Quadrat umgeben werden. Um die Richtung zu verändern, fügen wir nach der ersten Schleife eine weitere hinzu und lassen das Skript erneute von vorne laufen. Wichtig ist dabei, dass die Startposition der 2. Schleife die Endposition der 1. Schleife ist. Innerhalb der Schleife müssen die Bezeichnungen der neuen Punkte noch angepasst und verändert werden.
Definition der neuen Endposition und der neuen Ausgangslage
%Endposition wird an die zweite Schleife angepasst. Die neue Endposition entsteht durch die Endposition der ersten Schleife verknüpft mit einer zufälligen Bewegung neuPosX2=neuPosX+rand(Ny,Nx)-0.5; neuPosY2=neuPosY+rand(Ny,Nx)-0.5; %Nun startet die zweite Zeitschleife analog zur ersten for i=1:T*Zeitschritte Zwischenschritte von neuer Anfangsposition bis zur neue Endposition. "i" wird dabei von 1 bis T*Zeitschritte durchlaufen. Mit jedem folgenden "i" wird sich der neuen Endposition ein Stückchen mehr genähert. Erreicht "i" sein Maximum, ist der Zielpunkt erreicht. neuX2=neuPosX+(neuPosX2-neuPosX)*i*dt; neuY2=neuPosY+(neuPosY2-neuPosY)*i*dt;
Wie aus Modell b) bekannt werden nun die Abstände der Personen verglichen und die Neuinfizierten gezählt und markiert
figure (190-i)
title(['Radius=0.8, mehrfache Bewegung in t=' num2str(1+i*dt)])
axis([-2 22 -2 22]);
hold on;
%Auch hier wird die Position der zweiten Schleife angepasst. Der Rest wird nicht verändert
plot(neuX2,neuY2,'*g');
zahler=1;
for k1=1:length(IndInf1)
for j=1:Nx
for l=1:Ny
abstand=norm ( [neuX2(l,j)-neuX2(IndInf1(k1),IndInf2(k1)), neuY2(l,j)-neuY2(IndInf1(k1),IndInf2(k1))]);
if abstand<radiusInf
abstand;
plot(neuX2(l,j),neuY2(l,j), '*r') ;
%---------------------------
k2=1;
while k2 <=length(IndInf1)&&(l!=IndInf1neu(k2) || j!=IndInf2neu(k2))
k2=k2+1;
endwhile
if k2 >length(IndInf1)
IndInf1neu=[IndInf1neu l];
IndInf2neu=[IndInf2neu j];
endif
endif
endfor
endfor
endfor
IndInf1=IndInf1neu;
IndInf2=IndInf2neu;
hold off
Speichern der Bilder
Lauftext=["Fig_", num2str(190-i), ".jpg"] saveas((190-i), Lauftext) endfor
Nun haben wir einen Richtungswechsel generiert und können nach dem gleichen Prinzip beliebig oft die Richtung ändern.
%Wie oben beschrieben wird für die neue Schleife die Endposition aus Schleife 2 als Startposition für Schleife 3 definiert neuPosX3=neuPosX2+rand(Ny,Nx)-0.5; neuPosY3=neuPosY2+rand(Ny,Nx)-0.5; %Nun startet die dritte Zeitschleife analog zur zweiten for i=1:T*Zeitschritte %Passen die neue Position der entsprechenden Schleife an neuX3=neuPosX2+(neuPosX3-neuPosX2)*i*dt; neuY3=neuPosY2+(neuPosY3-neuPosY2)*i*dt;
Analoges Vorgehen wie in den ersten Schleifen
figure (170-i)
title(['Radius=0.8, mehrfache Bewegung in t=' num2str(2+i*dt)])
axis([-2 22 -2 22]);
hold on;
%Auch hier wird die Position der dritten Schleife angepasst. Der Rest wird nicht verändert
plot(neuX3,neuY3,'*g');
zahler=1;
for k1=1:length(IndInf1)
for j=1:Nx
for l=1:Ny
abstand=norm ( [neuX3(l,j)-neuX3(IndInf1(k1),IndInf2(k1)), neuY3(l,j)-neuY3(IndInf1(k1),IndInf2(k1))]);
if abstand<radiusInf
abstand;
plot(neuX3(l,j),neuY3(l,j), '*r') ;
%---------------------------
k2=1;
while k2 <=length(IndInf1)&&(l!=IndInf1neu(k2) || j!=IndInf2neu(k2))
k2=k2+1;
endwhile
if k2 >length(IndInf1)
IndInf1neu=[IndInf1neu l];
IndInf2neu=[IndInf2neu j];
endif
endif
endfor
endfor
endfor
IndInf1=IndInf1neu;
IndInf2=IndInf2neu;
hold off
Speichern der Bilder
Lauftext=["Fig_", num2str(170-i), ".jpg"]
saveas((170-i), Lauftext)
endfor
%Nun können nach dem gleichen Prinzip immer wieder neue Schleifen hinzugefügt werden. Bei jeder Schleife kommt es dann zu einer Richtungsänderung.
Für die untenstehende Annimation liesen wir 9-Mal den Zyklus laufen
Fazit und Optimierungsmöglichkeiten
Wir erhalten in der obigen Animation die Darstellung für einen Ansteckungsradius von 0.8 und einer sich ständig wechselnden Bewegungsrichtung. Optimieren bzw. verkürzen könnte man das Modell wenn man die Bewegungsänderung mit in die Zeitschleife packt.
Tutorium 2 - Fundamenallösungen der Diffusionsgleichung
[Bearbeiten]In der zweiten Tutoriumsaufgabe wird versucht die inhomogene Diffusionsgleichung analytisch zu lösen. Dabei soll zunächst die stationäre (zeitunabhängige) Diffusion betrachtet werden. Innerhalb dieses Kapitels werden dafür die Fundamentallösungen der Laplaceformel (homogene Gleichung) und der Poissonformel (inhomogene Gleichung) erläutert, dargestellt und deren Implementierung aufgezeigt. Im Anschluss wird die instationäre (zeitabhängige) Diffusion betrachtet, bevor abschließend die Lösungsformel eines Anfangswertproblem für die zeitabhängige Diffusionsgleichung implementiert wird.
Einführung in die Theorie
[Bearbeiten]
Zunächst wollen wir uns die Herleitung der homogenen Diffusionsgleichung näher anschauen. Im Allgemeinen beruht die Herleitung der homogenen Diffusionsgleichug auf zwei physikalischen Gesetzen:
Stationäre Diffusion im eindimensionalen Raum
[Bearbeiten]Nach dem Fick'schen Gesetz ist die Teilchenstromdichte (gibt an, wieviel Teilchen in einem Ort von links nach rechts diffundieren) proportional zum Konzentrationsgradienten, jedoch entgegen der Konzentrationsrichtung. Mathematisch ausgedrückt erhalten wir folgende Gleichung für die Teilchenstromdichte: Die Teilchen wandern also von einem Ort mit höherer Konzentration zu einem Ort mit einer niedrigeren Konzentration (Teilchen wandern in Richtung des Konzentrationsabfalls). Bezogen auf die aktuelle Modellierung bedeutet das, dass sich die Masse der Infizierten von den Ballungsräumen mit hoher Bevölkerungsdichte in Richtung der weniger besiedelten Gebiete ausbreitet.
Nach dem Massenerhaltungssatz kann eine Masse in einem System nicht verschwinden oder neu entstehen (sofern sie nicht extern hinzugefügt oder weggenommen wird. Nach dem Erhaltungsgesetz sollte sich die Gesamtanzahl der Teilchen in einem dem Intervall zwischen und , gegeben durch nicht ändern. Da es jedoch durch die Brownsche Molekularbewegung zum Austausch der Teilchen an den Rändern kommt, muss der Zufluss am linken Rand () mit dem Ausfluss am rechten Rand () ausgeglichen werden. Daraus erhalten wir folgende mathemische Gleichung:
Wird diese Gleichung nun durch geteilt so erhalten wir den Differenzenquotient
Dieser liefert für den Grenzübergang die sogenannte Erhaltungsgleichung
Da wir mit Hilfe des Fick´schen Gesetzes die Teilchenstromdichte mit ersetzen können, erhalten wir
Für einen konstanten Diffusionskoeffizienten ergibt sich dann Die entspricht gerade der Laplace Gleichung im eindimensionalen Raum.
Instationäre Diffusion im eindimensionalen Raum
[Bearbeiten]Die Herleitung der zeitabhängigen Diffusion im eindimensionalen Raum ist nahezu analog zum eben beschriebenen stationären Fall, jeodch ist die gesuchte Dichtefunktion nun zusätzlich noch von der Zeit t abhängig. Die Aussage des Fick´schen Gesetz ändert sich dadurch nicht. Jedoch muss beim Massenerhaltungssatz noch die zeitliche Veränderung angepasst werden: Das bedeutet, dass der Einfluss am linken Rand nicht mehr gleich dem Ausfluss am rechten Rand ist, sondern dass die Differenz der beiden Werte der zeitlichen Veränderung der Gesamtanzahl der Teilchen entspricht:
Analog zu obigen stationären Fall wird durch Teilen von und dem Grenzübergang der Differenzquotient gebildet und wir erhalten
In dieser Gleichung ersetzen wir wieder durch und wir erhalten die homogene Diffusionsgleichung bzw.
In beiden Fällen (stationär & instationär) wurde die Diffusionsgleichung mit den gleichen physikalischen Gesetzen hergeleitet. Leitet man aus dem Massenerhaltungssatz den Differenzenquotient ab und setzt man mit dem Fick´schen Gesetz die Teilchenstromdichte ein, so ergibt sich in beiden Fällen die homogene Diffusionsgleichung. Für die Herleitung der inhomogenen Diffusionsgleichung muss beachtet werden, dass ein Quellterm das Massenerhaltungsgesetz beeinflusst. Wird diese externe Quelle im Massenerhaltungsgesetz zusätzlich zum Ränderaustausch hinzugefügt, so kann nach dem gleichen Prinzip wie oben die Diffusionsgleichung hergeleitet werden. Da hier auf der rechten Seite eine externe Quelle den Term beeinflusst, sprechen wir von einer inhomogenen Diffusionsgleichung:
Stationäre (zeitunabhängige) Diffusion
[Bearbeiten]Implementierung der Fundamentallösung der Laplace Gleichung
Die Fundamentallösung der Laplace Gleichung der Laplace Gleichung lässt sich mit Hilfe der nachfolgenden Formel der Fundamentallösung für
- lösen.
Dabei stellt das Volumen der Einheitskugel in dar und ist die Vektornorm in .
Bei der Laplace Gleichung handelt es sich um eine stationäre Diffusion, d.h. sie ist unabhängig von unserer Zeitvariablen . Zudem ist die rechte Seite der Laplace Gleichung Null und wir haben somit keinen Quellterm, der in Bezug auf die Coronamodellierung ein Hotspot darstellen könnte. Wichtig ist das Beachten der Singularität der Fundamentallösung im Punkt , wo die Fundamentallösung gegen unendlich schießt.
Zuerst definieren wir unser Gitter. Wegen der Singularität der Fundamentallösung im Punkt wird der Abstand passend gewählt, damit der Punkt aus unserem Gitter "ausgeschnitten" wird.
step=0.01; %Schrittweite X = [-2:step:-0.01, 0.01:step:2]; %Vektor X von -2 bis 2 (Null ausgeschnitten) Y = [-2:step:-0.01, 0.01:step:2]; %Vektor Y von -2 bis 2 (Null ausgeschnitten) [x,y]=meshgrid(X,Y); %Gitter XY (Nullpunkt ausgeschnitten)
Im nächsten Schritt wird die Fundamentallösung der Laplace Gleichung in .definiert und anschließend graphisch ausgegeben.
phi=@(x,y) -log(sqrt(x.^2+y.^2))/(2*pi);
figure (1)
meshc(x,y,phi(x,y))%3D Plot
grid on
title('Fundamentallösung Laplace-Gleichung')
xlabel('x')
ylabel('y')
zlabel('z')
axis([-2 2 -2 2 -0.2 1])
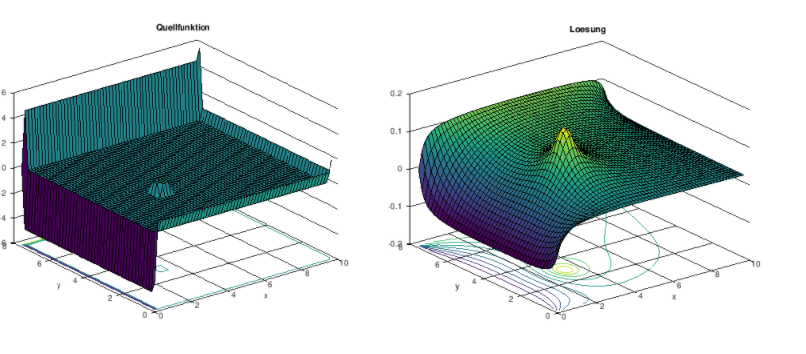
Diese Grafik beschreibt die Verteilung des Stoffes im festgelegten Raum ohne Quellfunktion. Im nächsten Schritt erfolgt die Darstellung der Poisson-Gleichungen, d.h. wir betrachten zusätzlichen einen Quellterm auf der rechten Seite der Gleichung.
Implementierung der Fundamentallösung der Poisson Gleichung
Die Lösung der inhomogenen Laplace Gleichung auf lässt sich mithilfe der Faltung zwischen der Fundamentallösung mit der Funktion der rechten Seite berechnen und bildet die nachfolgende Poissonformel:
Die Funktion stellt dabei eine Funktion mit kompakten Träger dar. Zudem ist der inhomogene Teil der Poisson Gleichung eine Quellfunktion, die im Zuge der Modellierung des Infektionsgeschehens der Coronapandemie ein Hotspot an Infektionen darstellen kann. Zur Programmierung der Fundamentallösung der Poissongleichung wird diese zuerst implementiert.
function wert=Quellfunktion(x,y) if sqrt((x.-0.3).^2+(y.-0.3).^2)<=0.1 wert=1; else wert=0; endif endfunction

Es ist gut erkennbar, dass die Quellfunktion einen kompakten Träger hat, d.h. innerhalb eines bestimmten Gebietes ist der Wert der Quellfunktion 1 und ansonsten Null.
Anschließend erfolgt die Implementierung der Faltung. Hierfür wird erneut unser rechteckiges Gitter als Ausgangssituation definiert.
clear all; close all; step=0.03; X=[0:step:2]; Y=[0:step:2]; [x,y]=meshgrid(X,Y);
Im nächsten Schritt werden nun die Funktionswerte in allen Punkten definiert und die Quellfunktion in eine Ecke des Gitters eingebaut.
for i=1:(length(X)) for j=1:(length(Y)) f(j,i)=1*Quellfunktion_1(x(j,i),y(j,i)); endfor endfor
Anschließend folgt die Implementierung der Poissonformel zur Lösung der Poissongleichung für ein unbeschränkten Gebiet im . Die Werte der Fundamentalfunktion werden um ein festes x* verschoben und in einer Matrix φ gespeichert. Durch Verwenden einer for-Schleife werden die verschobenen Werte in einer Matrix gespeichert, damit die Differenz der Argumente als Differenz von Matrizen gegeben ist. Um den Punkt der Singularität zu umgehen, wird φ(x*−x)=0 gesetzt für x*≡x. Das doppelte Integral wird mit der Trapezregel numerisch gelöst.
for i=1:(length(X))
for j=1:(length(Y))
xstar=x(j,i)*ones(length(Y),length(X)); %Verschiebung um ein festes x*
ystar=y(j,i)*ones(length(Y),length(X)); %Verschiebung um ein festes y*
% Phi mit verschobenem Argument:
phi=-log(sqrt((xstar.-x).^2+(ystar.-y).^2))/(2*pi); %Speicherung der verschobenen Werte in Phi
phi(j,i)=0;
%numerische Integration
I(j,i) = trapz(Y,trapz(X,phi.*f,1),2);
endfor
endfor
Die graphische Ausgabe der Poisson Gleichung wird durch den folgenden Code dargestellt.
figure 1
meshc(x,y,I)
grid on
title ('Loesung der Poisson-Gleichung')
xlabel('x')
xlabel ('y')
view([0,2,-1])
Diese Grafik beschreibt die Verteilung des Stoffes im festgelegten Raum ausgehend von der oben definierten Quellfunktion. Weiterführend dient diese Lösung der Poisson-Gleichung als Anfangsbedingung für die instationäre Gleichung.
Instationäre (zeitabhängige) Diffusion
[Bearbeiten]Homogene, instationäre (zeitabhängige) Diffusion
Für die homogene instationäre (zeitabhängige) Diffusionsgeichung , mit und konstanten Diffusionskoeffizient .
existiert auf einem unbeschränkten Gebiet die nachfolgende Lösungsformel:
wobei das Quadrat der euklidischen Norm von ist. Es ist erkennbar, dass im Punkt eine Singularität vorhanden ist und diese bei der Implementierung nun wieder aus dem Gitter entfernt werden muss. Dadurch, dass der Diffusionskoeffizient eine Konstante ist, sollte diese Formel nur für Modellierungsansätze angewendet werden, die nicht vom Ort abhängig sind.
Die Vorgehensweise ähnelt der vorherigen. Zuerst wird ein Gitter definiert, das die Singularität an der Stelle ausschneidet.
step=0.01; %Schrittweite X = [-2:step:-0.04, 0.04:step:2]; %Vektor X von -2 bis 2 (Null ausgeschnitten) Y = [-2:step:-0.04, 0.04:step:3]; %Vektor Y von -2 bis 2 (Null ausgeschnitten) [x,y]=meshgrid(X,Y); %Gitter XY (Nullpunkt ausgeschnitten)
Daraufhin wird der Diffusionskoeffizient definiert und eine Zeitschleife erstellt, um die Abhängigkeit von zu definieren.
a=0.2; %Konstanter Diffusionskoeffizient T=3; %Anzahl der Zeiteinheiten Zeitschritte=3; %Anzahl der Zeitschritte dt=1/(Zeitschritte*T); %Zwischenschritte t_0=0.1; %Anfangsbedingung
Nun folgt die Eingabe der obigen Fundamentallösung der homogenen instationären Diffusionsgleichung mit der anschließenden graphischen Ausgabe.
for i=0:T*Zeitschritte;
t=t_0+i*dt;
psi=@(x,y,t) 1/(4*pi*a*t)*exp(-sqrt(x.^2+y.^2)/(4*a*t));
figure (i+1)
meshc(x,y,psi(x,y,t))
grid on
title(['Zeitabh�ngige Diffusion nach t=',num2str(t_0+i*dt)])
xlabel('x')
ylabel('y')
zlabel('z')
axis([-2 2 -2 2 0 1.1])
endfor
In der Animation ist gut zu erkennen, dass mit zunehmender Zeit der Stoff, bzw. im Rahmen der Infektionsmodellierung die Anzahl der Infizierten, abflachen und nach außen diffundieren. Ohne externe Quelle bzw. ohne neue Infektionsquellen flachen die Infektionszahlen ab und die "Hügel" verteilt sich auf die umliegenden Gebiete und wird immer kleiner.
Nun wird in der letzten Aufgabe des Tutoriums 2 diese Diffusionsgleichung mit einer Anfangsbedingung zu einem Anfangswertproblem ergänzt.
Anfangswertproblem der homogenen, instationären (zeitabhängigen) Diffusionsgleichung
Die Diffusiongleichung , mit und konstanten Diffusionskoeffizient .
wird mit einer Anfangsbedingung ergänzt, die im Anfangszeitpunkt die Konzentrationsdichte bzw. die Dichte der Infizierten beschreibt. Die Lösung dieses homogenen Anfangswertproblems für ist durch die Faltung der Fundamentallösung mit der Anfangsfunktion gegeben:
Diese Faltung ist beschränkt, wenn die Anfangswertfunktion beschränkt ist. Da in eine Singularität hat, ist auch dieses Anfangswertproblem in singulär.
Nun kommen wir zur Programmierung des Anfangswertproblems. Die Quellfunktion wurde aber zuerst so abgeändert, damit wir nun drei Infektionsherde haben.
function wert=Quellfunktion_2(x,y) if sqrt((x.-0.3).^2+(y.-0.3).^2)<=0.1 wert=1; else wert=0; if sqrt((x.-0.3).^2+(y.-1.3).^2)<=0.2 wert=0.8; else wert=0; if sqrt((x.-1.5).^2+(y.-0.3).^2)<=0.07 wert=0.5; else wert=0; endif endif endif endfunction
Es folgt nun wieder das analoge Erstellen unseres Gitters.
clear all; close all; step=0.03; X=[0:step:2]; Y=[0:step:2]; [x,y]=meshgrid(X,Y);
Nun wird der Diffusionskoeffizient initialisiert und die zeitliche Komponente eingebunden.
a=0.2; %Konstanter Diffusionskoeffizient T=3; %Anzahl der Zeiteinheiten Zeitschritte=3; %Anzahl der Zeitschritte dt=1/(Zeitschritte*T); %Zwischenschritte t_0=0.1; %Startzeit
Anschließend werden die Funktionswerte in allen Punkten definiert und die Quellfunktion mit ihren drei Infektionshotspots in der Anfangsbedingung initialisiert. Letztere werden auf unsererm Gitter als unbeschränktes Gebiet verteilt.
for i=1:(length(X)) for j=1:(length(Y)) u0(j,i)=1*Quellfunktion_2(x(j,i),y(j,i)); endfor endfor
Im finalen Schritt zu Berechnung folgt nun die Implementierung der Faltung :. Die zeitliche Abhängigkeit wird durch das Einfügen einer Zeitschleife gesichert.
for s=0:T*Zeitschritte
t=t_0+s*dt
for i=1:(length(X))
for j=1:(length(Y))
xstar=x(j,i)*ones(length(Y),length(X)); %Verschiebung um ein festes x*
ystar=y(j,i)*ones(length(Y),length(X)); %Verschiebung um ein festes y*
% Psi mit verschobenem Argument:
psi=(1/(4*pi*a*t))*exp(-(((xstar.-x).^2+(ystar.-y).^2))/(4*a*t)); %Speicherung der verschobenen Werte in Psi
%numerische Integration
I(j,i,s+1) = trapz(Y,trapz(X,psi.*u0,2));
endfor
endfor
Abschließend fehlt nur noch das Plotten der Bilder.
figure (s+1)
meshc(x,y,I(:,:,s+1))
grid on
title(['Hier könnte der Titel stehen=', num2str(t_0+s*dt)])
xlabel('x')
ylabel('y')
zlabel('z')
axis([0 2 0 2 0 0.35]) %feste Achsen für Vergleich besser
Tutorium 3 - Modifiziertes SIR Modell
[Bearbeiten]
Exponentielles Wachstum
[Bearbeiten]Bei diesem Modell gehen wir davon aus, dass die Anzahl der Infizierten im neuen Zeitpunkt aus den Infizierten im alten Zeitpunkt und den in diesem Zeitabschnitt Neuinfizierten besteht. Mathematisch formuliert erhalten wir folgende Gleichung:
- wobei die Infektionsrate bezogen auf eine Zeiteinheit ist.
Durch das Teilen der Gleichung
mit und nach dem Grenzübergang folgt mit dem ersten Differenzenquotineten das exponenzielle Wachstumsmodell:
mit Exponentialfunktion als Lösung
Die Tatsache, dass mit der erhaltenen DGL die Anzahl der Infizierten unendlich ansteigt, macht deutlich, dass dieses Modell für die Modellierung einer Pandemie mit angepasst werden muss. Wir betrachten also im Folgenden das logistische Wachstum.
Logistisches Wachstum
[Bearbeiten]Der Aufbau des logistischen Modells ähnelt dem eben beschriebenen exponentiellen Modell. Jedoch wird hier zusätzlich beachtet, dass die Anzahl der Infizierten nicht unendlich steigen kann, sondern gesättigt ist, wenn die Gesamtpopulation erreicht wurde. Mathematisch spiegelt sich dies in folgender Gleichung wieder:
- , wobei die freie Kapazität beschreibt (also gerade die Anzahl an Personen, die noch infiziert werden können).
Analog zum obigen Modell, bilden wir den ersten Differenzenquotienten und erhalten folgende DGL:
mit logistischer Funktion als Lösung:
Der neu hinzugefügte Term bewirkt also, dass mit zunehmender Anzahl an Infizierten der Anstieg der Infizierten abflacht bis hin zu Sättigung der (Infizierten-) Population, also genau wenn ist.
SI-Modell
[Bearbeiten]Zur Modellierung der dritten Tutoriumsaufgabe betrachten wir zuvor verschiedene Kompartimentmodelle. Vereinfacht gesagt teilen Kompartimentmodelle für die Infektionsverbreitung die Bevölkerung in verschiedene Gruppen immunologischer Stadien. Das einfachste Modell hiervon ist das SI-Modell.
Innerhalb des SI-Modell wird die Gesamtpopulation in zwei Gruppen eingeteilt: für die kommmulierten Infizierten und für den infektionsanfälligen Teil der Bevölkerung. Genesene Individuen aus der Gruppe der Infizierten sind zudem nach einer Infektion gegen weitere Infektionen immun und können nicht mehr in die Gruppe der Infektionsanfälligen wechseln. Auf Grund des logistischen Wachstums wird es auch als logistisches Modell bezeichnet.
Zu Beginn gibt es nur eine infizierte Person und die Gruppe der Infektionsanfälligen besteht somit aus der gesamten Population.
Diese bilden die Anfangsbedingungen für unsere nachfolgenden gewöhnlichen Differentialgleichungen.
Die Veränderungsrate der Infektionsanfälligen ist abfallend, also verkleinert sich der Bevölkerungsteil der Anfälligen.
Die Veränderungsrate der Infizierten wird als logistische DGL formuliert und wächst analog zu dem abfallenden Anteil der Gruppe
Aus beiden Differentialgleichungen lässt sich die Erhaltungsgleichung folgern, die besagt, dass die Gesammtpopulation konstant erhalten bleibt, also die Population nicht größer oder kleiner wird, sondern sich nur die Gruppen innerhalb der Population verändern.
Kritisieren lässt sich an diesem SI-Modell, dass die Populationsentwicklung durch Neugeborene und Verstorbene nicht genau betrachtet werden. Verstorbene Infizierte sind zur Gruppe zugehörig.
SIR-Modell
[Bearbeiten]Als eine Weiterentwicklung des SI-Modell lässt sich das SIR-Modell nennen. Hier wird eine Gruppe der genesenen Individuen ergänzt. Dazu gehören infizierte Individuen, die nach einer Infektion entweder genesen oder versterben - also aus der Gruppe der Infizierten nach einer Infektion in die Gruppe mit einer bestimmten Wechselrate wechseln. Auch das SIR-Modell besteht aus einem System von Differentialgleichungen - dieses Mal drei, da es auf drei Gruppen baut. Es besteht zudem ein Zusammenhang zum SI-Modell, der sich wie folgt darstellen lässt: Die kumulierten Infizierten setzen sich aus den derzeitigen Infizierten und zusätzlich den Genesenen bzw. Toten zusammen, also aus .
Für die Gruppe der Anfälligen gilt analog zum SI-Modell . Für die Gruppe der Infizierten gilt ähnlich zum SI-Modell , nur mit der Änderung, dass ein Teil der Gruppe der Infizierten mit der Wechselrate abgezogen wird, der in die Gruppe der Genesenen/Toten wandert. Für die Gruppe der Genesenen/Toten gilt dabei , wobei sich die Wechselrate mit als Umkehrwert der Genesungszeit berechnen lässt. Im Falle der Coronapandemie wäre der Faktor , da man nach einer Infektion von einem Zeitraum von 14 Tagen ausgeht, innerhalb dessen man infektiös ist. Auch wie im SI-Modell gilt auch im SIR-Modell die Erhaltungsgleichung , die besagt, dass die Gesammtpopulation konstant erhalten bleibt, also ein Wechsel der Individuen nur innerhalb der Gruppen der Population geschieht.
Modifiziertes SIR-Modell
[Bearbeiten]Werden die gestorbenen Infizierten nicht in der Gruppe der Genesenen erfasst, so sprechen wir vom modifizierten SIR-Modell. Innerhalb dieses Modells bildet die Funktion nur einen Bruchteil der Infizierten ab - nämlich diejenigen Individuen, die tatsächlich erkrankt sind und bspw. durch positive Tests erfasst wurden. Wir benutzen folgende Variablen:
als unsere Infektionsrate (in SI-Modell ist diese ),
als konstante Sterberate, die angibt, in welchem Anteil die verstorbenen Infizierten aus der Gesamtpopulation ausscheiden und
als konstanten Faktor, der den prozentualen Anteil der richtig positiv getesteten Infizierten angibt, die erkrankt sind - also den prozentualen Anteil der entdeckten Infizierten; Ist , so liegt der Anteil der gemeldeten Infizierten bei und aller Infizierten wurden nicht gemeldet bzw. entdeckt, weil z.B. die Individuen keine Symptome gezeigt haben und somit keinen Anlass für eine Testung geboten haben. Ist , dann wird jeder Infizierte der Population getestet und entdeckt. Ist und , so erhalten wir unser klassisches SIR-Modell.
Aus obigen Variablen bilden wir das nachfolgende System gewöhnlicher Differentialgleichungen.
Neu in dieser Gleichung ist der Vorfaktor , der die Infektionsrate in Abhängigkeit von den prozentualen Anteil der positiv getesteten Infizierten angibt.
Hier wird mit der Berechnung von der Anteil der Verstorbenen, die ansonsten in die Gruppe wandern, abgezogen.
Für das System dieser drei Differentialgleichungen erhalten wir noch foglende Anfangsbedingungen:
Charakteristisch für das modifizierte SIR-Modell ist unsere Erhaltungsgleichung , die besagt, dass sich, anders als vorher, die Gesamtpopulation um die verstorbenen Infizierten verringert, da diese aus der Gruppe abgezogen werden.
Ziel der Tutoriumsaufgabe 3 ist das Abbilden des Infektions- und Impfgeschehens als modifiziertes SIR Modell.
Zunächst soll eine geeignete Basisinfektionsrate c gefunden werden, die das exponentielle Wachstum bis Ende April 2020 gut abbildet. Das Wachstum der Infizierten war zu Beginn der Pandemie bis Ende April (genauer: die ersten 30 Tage) annähernd exponentiell, da keine geeigneten Gegenmaßnahmen getroffen wurden, um den exponentiellen Infektionsanstieg zu verringern. Hierfür haben wir folgende zwei Möglichkeiten genutzt, um die passende Basisinfektionsrate zu finden.
Aufgabe 1.1a: Finden der Basisinfektionsrate mit Augenmaß
[Bearbeiten]
Zu Beginn einer Pandemie verhält sich der Anstieg der Infizierten annähernd exponentiell und unbeschränkt, da fast die gesamte Bevölkerung empfänglich ist und noch keine Gegenmaßnahmen ergriffen wurden. Nun geben wir verschiedene Werte für Infektionsrate ein und bestimmen per Augenmaß, welche am ehesten die realen Werte (rote Punkte) abbildet. Wir betrachten dazu die ersten 30 Tage inkl. des realen Startwertes von 17 Infizierten am Tag 0.
Infektionsrate=0.265; Startwert=17; %Infizierte zum Zeitpunkt t=0 EndZeitpunkt=30; %wie viele Tage werden betrachtet Tage=[1:1:EndZeitpunkt]; %Betrachtung bis Ende März f1=Startwert*exp(Infektionsrate*(Tage)); %definiere Exponentialfuktion
%Plotten des exponentiellen Wachstums und der echten Fälle
figure(1)
plot (zeit, AlleInfizierte, '*r', Tage, f1, '-b');
title (['Infizierte Deutschland und Expo.-Funktion mit Infektiosnrate = '
num2str(Infektionsrate)]);
xlabel ('Tage ab dem 26. Februar')
ylabel ('Personen')
grid on
axis([0, 30, 0 , 28000])
Der Code hierzu ist ziemlich selbsterklärend und trivial. Es sollte aber erwähnt werden, dass wir auf eine externe coronaData Funktion zugegriffen haben, die wir mit den offiziellen Infektionszahlen (und später auch Impfzahlen) des Robert-Koch-Institutes gefüllt haben. Bei der Infektionsrate wurden Werte ausprobiert, die zwischen 0,2 und 0,3 liegen. Folglich erschien die Infektionsrate 0,265 als kompatibelste für unsere geplotteten Daten.
Aufgabe 1.1b: Finden der Basisinfektionsrate mit Hilfe der Regression
[Bearbeiten]Eine präzisere Methode zur Findung der Basisinfektionsrate ist das Verfahren der exponentiellen Regression. Ziel ist es für jeden Datenpunkt ein möglichst geringes Residuum zu finden, damit die Abweichungen zu den ursprünglichen Daten - das Fehlermaß - nicht zu groß ist. Mit Hilfe jener finden wir schließlich die Regressionskurve. Interessant und erwähnenswert im Code ist zudem die zweifache for-Schleife: Innerhalb der ersten for-Schleife wird in dem Intervall der Probeparameter das Minimum des Residuums bezüglich der Wachstumsrate für einen festen Anfangswert gefunden, während bei der zweiten for-Schleife noch ein zweites Minimum bezüglich gesucht und gefunden wird. Das Resultat dieser beiden for-Schleifen ist ein finaler Index I, innerhalb dessen das Residuum minimal - folglich die Abweichungen zu den Datenpunkten ebenfalls minimal sind.
%Probeparameter
for j=-MaxN/10:2*MaxN
aj=a+j*a*10/MaxN;
for i=-MaxN:MaxN
ki=k+i*k/MaxN;
%Berechnung Residium
res(i+MaxN+1)=norm ((expon(zeit,ki,aj)-AlleInfizierte),2); %Residuum als Differenz zweier Vektoren)
%Minimum des Residuums R bzgl. Wachstumsrate für festen Anfangswert
if res(i+MaxN+1)==min(res)
Ind=i;
kopt= [kopt ki];
res_vector=[res_vector min(res)];
a_vector=[a_vector aj];
endif
endfor
%Minimum des Residuums bezüglich j (zweite for Schleife)
resMatrix(j+MaxN/10+1,:)= res;
endfor
for i=2:length(res_vector)
if res_vector(i)==min(res_vector(2:length(res_vector)))
Ind2=i;
endif
endfor
koptvec=kopt;
kopt=kopt(Ind2);
res_vector(Ind2);
a_vector(Ind2);
Im Zuge dessen erhalten wir nun neben unserer finalen optimalen Infektionsrate k zur Beschreibung des Infektionsgeschehens k=0.19610 zusätzlich auch einen optimalen Anfangswert 78.400 und ein optimales Residuum von 2279.3. Vergleicht man die beiden Graphen der Infektionszuwächse - den mittels Augenmaß abgeschätzten und den durch Regression berechneten - dann fällt auf, dass beide Graphen zu Beginn sehr nah an den Datensätzen liegen und erst ab Tag 20 sich der durch Regression bestimmte Graph als präzisere Graph kennzeichnet.
Aufgabe 2.1: Erweitern und Plotten der Corona-Data Funktion/Datenbank
[Bearbeiten]Die in der Coronadata Funktion enthaltenen Daten wurden mit den offiziellen Daten des RKIs bis Anfang Mai 2021 erweitert.
Mit Hilfe der abgebildeten Daten lässt sich klar das Infektionsgeschehen und das Wirken der Maßnahmen nachträglich beschreiben. Es fällt auf, dass die Kurve mit den aktuellen Infizierten ihren Peak nach ungefähr 300 Tagen nach dem 26. Februar, also ungefähr zu Beginn des Jahres 2021, hatte, im Anschluss daran zunächst etwas gefallen ist, wie beispielsweise durch den Start der Impfstoffverteilung Ende 2021, wodurch zu Beginn vor allem Ältere und gefährdete Personen vor einer möglichen Infizierung mit dem Coronavirus geschützt wurden. Am 14. Januar 2021 wurden zudem die Einreiseregeln aus Risikogebieten verschärft. Ab dem ungefähr 375 Tag nach Februar 2020, also knapp ein Jahr später im Februar 2021, steigt die Kurve der aktuell Infizierten erneut an, bevor sie schließlich nach ihrem Peak am 425 Tag nach Februar 2020 - ungefähr März 2021 - wieder anfängt zu sinken. Der erneute Anstieg lässt sich mit dem Auftreten der Mutationen - am 17. Februar 2021 wurde bezüglich der Variante aus Großbritannien gewarnt - erklären. Zeitgleich nehmen aber zwei weitere Bausteine in der Virusbekämpfung an Geschwindigkeiten an Fahrt auf: Die Zahl der Geimpften steigt nun zunehmend an und zusätzlich gewinnt auch die Testkampagne an Bedeutung: Ab Anfang März 2021 können sich alle Bürger kostenlos mit Schnelltests in Testzentren auf das Coronavirus testen lassen, um somit möglichst frühzeitig mögliche Infektionsherde ausschließen zu können. Über Ostern, Ende März 2021, wird schließlich die Notbremse als weitere Maßnahme vereinbart, um beim Überschreiten der Inzidenz von 100 möglichst viele Kontakte mit potentiellen Infizierten zu vermeiden. Zusätzlich gelingt es durch den Start der Impfungen in den Hausarztpraxen Anfang April 2021 die Impfkampagne weiter voranzutreiben. Vermutlich ist es eine Mischung aus all diesen Maßnahmen, die zu unserer Verlangsamung des Infektionsgeschehens führt, die bis dato anhält.
Aufgabe 2.2: Klassisches SIR-Modell
[Bearbeiten]Nun stellen wir das SIR-Modell dar und benutzen dabei die Infektionsrate aus der Aufgabe 1.1a. Zunächst aber ein kurzer Exkurs in die Theorie des SIR-Modells. Es dient zur Modellierung der Ausbreitung von Krankheiten, an Hand dessen eine Prognose über den Verlauf der Krankheit gemacht werden kann und wurde 1927 von William O. Kermack und Anderson G. McKendrick erstmals publiziert. Innerhalb des Modells befindet sich jedes Individuum einer Population der Größe in einem der folgenden drei Zustände:
: susceptible, d.h. für die Krankheit anfällig und potentiell infizierbar
: infected, d.h. infiziert
: recovered/removed/resistant, d.h. entweder ist das Individuum genesen nach der Infektion, gestorben oder resistent auf Grund einer Impfung. Innerhalb dieser Implementierung wird aber letzteres noch nicht betrachtet.
Der klassische Weg eines Individuums dieser Population lässt sich von nach nach beschreiben. Zu jedem Zeitpunkt gilt dabei für unsere Populationsgröße . Weiterhin gilt für die Gesamtpopulation die Erhaltungsgleichung : die besagt, dass die gesamte Population konstant erhalten bleibt und von außen keine neuen Individuen dazukommen oder weggehen. Grundlage zur Modellierung des SIR-Modells ist außerdem das System nachfolgender gekoppelter Differentialgleichungen.
- , beschreibt die Funktion der Empfänglichen, wobei k die Infektionsrate aus Aufgabe 1.1a ist
- , beschreibt die Funktion der Infizierten
-
, beschreibt die Gesundungsfunktion,
wobei die Rate sich als Umkehrwert der Genesungszeit T (infektiöser Periode) berechnet.
Zur Implementierung bestimmen wir zunächst unsere Parameter, die fest bleiben. Wir gehen dabei von einer Kapazität aus, die von entspricht. Unsere Infektionsrate übernehmen wir aus Aufgabe 1.1a. Da wir von einer Krankheitszeit von 14 Tagen ausgehen, setzen wir die Genesungsrate auf . Als zeitliches Fenster wird der Zeitraum der ersten 447 Tage, also von Beginn der Pandemie bis aktuell (Mitte Mai 2021) betrachtet.
Kapazitaet=55000; Infektionsrate=0.265; Genesungsrate=1/14; zeit=(0:1:447); Anfangsinfizierte=16/1000; Anfangsgenesene=0;
Nun stellen wir als Spaltenvektor die verschiedenen drei Gruppen zu Beginn der Pandemie dar.
yo=[Kapazitaet-Anfangsinfizierte; Anfangsinfizierte; Anfangsgenesene]
Im nächsten Schritt wird die Funktion der rechten Seite unseres Differentialgleichungssystems implementiert. Da wir davon ausgehen, dass die Gesamtpopulation konstant bleibt und es weder Geburten noch Tode gibt, die in dem Modell dazukommen oder entfernt werden, gilt und wir erhalten folgende Funktionen, die wir für unsere Funktion des Differentialgleichungssystems implementieren.
f=@(y,x) [-Infektionsrate*y(1)*y(2)/Kapazitaet; +Infektionsrate*y(1)*y(2)/Kapazitaet-Genesungsrate*y(2); +Genesungsrate*y(2)];
Um die Lösung unseres DGL zu erhalten, nutzen wir die in Octave integrierte Funktion zur numerischen Lösung und plotten diese im Anschluss.
y=lsode(f, yo, zeit);
figure (30)
plot(zeit, y (:,1), '-', zeit, y (:,2),'-', zeit, y (:,3), '-', zeit, y (:,3)+ y (:,2),'-')
legend ("Empfängliche", "Infizierte", "Genesene/Tote", "kumulierte Inzizierte", "location", "east")
axis([0 447 0 56000])
Innerhalb der graphischen Darstellung lässt sich gut erkennen, dass die Anzahl der Infizierten zunächst exponentiell steigt, dann aber ungefähr ab Tag 80 nach Zeitbeginn ihren Peak hat und im Anschluss schnell sinkt. Dies steht in einem Zusammenhang mit der Gruppe der Empfänglichen, deren Anzahl während des exponentiellen Wachstums der Infiziertenkurve stark fällt und somit folglich weniger Infizierte ermöglicht. Für weitere Interpretationen diesbezüglich verweisen wir an dieser Stelle auf Kapitel XYZ zu Beginn dieser Seite.
Aufgabe 2.3: Modifiziertes SIR-Modell / Aufgabe 3 - Auswirkungen Veränderung Parameter r
[Bearbeiten]In dieser Aufgabe wurde das modifizierte SIR-Modell implementiert. Zunächst auch hier wieder ein Ausflug in die Theorie dieses Modells. Das modifizierte SIR-Modell bildet mit der Funktion nur ein Bruchteil der Infizierten ab, die tatsächlich erkrankt sind und im System erfasst werden. Zudem wird nun eine Verlangsamungsfunktion eingeführt, die auf Grund der beschlossenen Maßnahmen die Infektionsrate verlangsamt. Mit dieser Anpassung soll somit eine Anpassung an die vom Robert-Koch-Institut ermittelten, tatsächlichen Infektionszahlen in Deutschland erzielt werden.
Es gilt nun
- ,
Wie oben festgehalten ist
- die zeitabhängige Infektionsrate,
- die Kapazitätsgrenze, d.h. der Bevölkerungsanteil, der sich ansteckt,
- die Basisinfektionsrate, die das exponentielle Wachstum zu Beginn der Pandemie beschreibt
- die tägliche Wechselrate von der Gruppe der Infizierten in die Gruppe der Genesenen oder Toten ()
- die Todesrate.
Es gilt zudem das Erhaltungsgesetz . Bei , d.h. es werden weder Tote noch Genesene mitgezählt, folgt . Ist der Anteil der erfassten Infizierten , dann erhalten wir obiges originales SIR-Modell.
Die Implementierung erfolgt analog zu Aufgabe 2.2, nur einzig allein müssen wir darauf achten, dass wir unseren Wert ebenfalls initialisieren und die richtigen Funktionen implementieren. Somit gilt für unsere Parameter
Kapazitaet=55000; Infektionsrate=0.265; Genesungsrate=1/14; Todesrate=0.003; zeit=(0:1:447); Anfangsinfizierte=16/1000; Anfangsgenesene=0; r=0.2; Anfangstote=0;
und unsere Startwerte in einem Spaltenvektor:
yo=[Kapazitaet-Anfangsinfizierte; Anfangsinfizierte; Anfangsgenesene; Anfangstote];
Nun definieren wir unser DGL-System, das wir anschließend numerisch mit Octave lösen.
f=@(y,x) [-Infektionsrate*y(1)*y(2)/(Kapazitaet*r);
+Infektionsrate*y(1)*y(2)/Kapazitaet-Genesungsrate*y(2);
+Genesungsrate*y(2)-Todesrate*y(2)
Todesrate*y(2)];
y=lsode(f, yo, zeit);
figure (31)
plot(zeit, y (:,1), '-', zeit, y (:,2),'-', zeit, y (:,3), '-', zeit, y (:,3)+ y (:,2),'-', zeit, y (:,4), '-')
title (['mod. SIR-Model mit r=' num2str(r)]);
legend ("Empfängliche", "Infizierte", "Genesene", "kumulierte Inzizierte", "Tote", "location", "east")
axis([0 447 0 56000])
xlabel ('Tage')
Nach dem Plotten erhalten wir dann die nachfolgende graphische Lösung.
Vergleicht man diese Abbildung mit der Abbildung des normalen SIR-Modells, so fällt einem die Rolle des Parameters auf. Je kleiner ist, desto weniger tatsächlich infizierte Personen werden erfasst, d.h. wir haben eine hohe Dunkelziffer an nicht erkannten Infektionen. Ist , dann wurden alle Infizierten entdeckt und wir haben das klassische SIR-Modell. Ist , dann würden mehr Menschen positiv getestet werden, als tatsächlich infiziert sind, d.h. es würde viele falsch-positive Testergebnisse geben. Demnach können wir also davon ausgehen, dass wir zu Beginn der Pandemie einen kleinen - Wert hatten, da die Dunkelziffer nicht erkannter Infektionen auf Grund mangelnder Testkapazitäten und fehlendem Wissen im Umgang mit dem Virus - es wurden zunächst nur Menschen mit Symptome getestet - recht hoch und so bspw. symptomlose Infizierte unentdeckt blieben. Nachfolgende Simulation stellt das modifizierte SIR-Modell für unterschiedliche -Werte dar.
Aufgabe 2.4: Die Verlangsamungsfunktion/Slowdown-Funktion
[Bearbeiten]Um die Slowdown-Funktion approximieren zu können, vergleichen wir zunächst die realen Werte des RKIs mit den Daten des modifizierten SIR-Modells. Hierfür stellen wir beiden Daten in einer Abbildung dar und vergleichen die jeweiligen Kurven miteinander.
Zuerst greifen wir auf unsere Daten des SIR-Modells aus Aufgabe 2.1 zurück
A=coronaData(); AlleInfizierte=A(1,:); % die erste Zeile der Matrix wird "AlleInfizierte" genannt AlleToten=A(2,:); % die zweite Zeile der Matrix wird "AlleToten" genannt AlleGenesene=A(3,:); % die dritte Zeile der Matrix wird "AlleGenesene" genannt aktuelleFaelle=AlleInfizierte-AlleGenesene; % die aktuellen Fälle werden in der Matrix nicht angegeben, lassen sich aber einfach zum Zeitpunkt x berechnen = AlleInfizierte-AlleGenesene n=length(AlleInfizierte); % gibt mir die Länge der Zeile innerhalb der Matrix an zeitA=[0:1:n-1];
Nun plotten wir die Daten aus unserer Datenbank zusammen mit den Daten unseres modifizierten SIR-Modells.
figure(666)
title ('Vergleich RKI mit Model')
plot (zeitA, AlleInfizierte./1000, '*c', zeitA,aktuelleFaelle/1000, '*r' , zeitA,AlleGenesene/1000,'*g', zeit, y (:,2),'r-', zeit, y (:,3), 'g-', zeit, y (:,3)+ y (:,2),'c-')
xlabel ('Tage ab dem 26. Februar')
ylabel ('Zahlen in Tausend')
legend ( "kumulierte Infizierte (RKI)" ,"aktuell Infizierte (RKI)","genesen/imun (RKI)" , "Infizierte (Model)", "Genesene (Model)", "kumulierte Inzizierte (Model)", "location", "north")
grid on
axis([0,n, 0 ,4000])
Damit die Darstellung übersichtlicher ist werden Daten des gleichen Typs mit der gleichen Farbe dargestellt. Die "dünnen" Kurven entsprechen den Daten unseres modifizierten SIR-Modells und wollen wir nun mit Hilfe der Slowdown-Funktion so verändern, dass sie unseren "fetten" Kurven, den tatsächlichen Daten des RKIs, entsprechen.
Für die Slowdown-Funktion brauchen wir das folgende Hintergrundwissen bezüglich des bisherigen epidemiologischen Verlaufs. Bis zum Tag 35 steigen die Werte nahezu exponentiell an, weil die Entwicklung der Epidemie unterschätzt wurde und Maßnahmen zunächst vermieden wurden. Nach knapp 40 Tagen dagegen macht sich der erste Lockdown bemerkbar und die Anzahl der Neuinfizierten sinkt. Beschlossen wurde diese Maßnahme zwar schon ab Tag 30 nach Pandemiebeginn, jedoch benötigen alle beschlossene Maßnahmen auch Zeit um wirken zu können. Im Anschluss wurden bis zum Tag 200 weitere Maßnahmen ergriffen, wie zum Beispiel eine verschärfte Maskenpflicht und Kontaktbeschränkungen. Zeitgleich fanden aber auch erste Lockerungen wie Schulöffnungen mit Wechselunterricht statt. Ab Tag 200 folgen weitere Lockerungen und in den Schulen befinden sich die Klassen nun vollständig im Präsenzunterricht. Die Kontaktbeschränkungen werden gelockert und ein Reisen über die Sommermonate ermöglicht. In Folge dessen steigen die Zahlen der Neuinfektionen relativ schnell an, sodass ein erneuter Lockdown notwendig ist. Erstmalig als "Lockdown light" eingeführt, wurde dieser zwei Wochen später verschärft und wirkt erst ab Tag 300. Es ist ersichtlich, dass die Bevölkerung sich über die Weihnachtszeit an die Regeln gehalten hat, da die Zahlen nun wieder fallen. Knapp ein Jahr nach Ausbruch der Pandemie steigen die Zahlen der Infizierten erneut rasant, was sich mit dem Auftreten der britischen Mutante erklären lässt, welche sich leichter verbreitet. Die daraufhin angewendete "Bundesnotbremse" und erste Erfolge der Impfkampagne führen dazu, dass jedoch nach kurzer Zeit die Kurve der Neuinfektionen wieder fällt.
All diese Auswirkungen implementieren wir für wie folgt.
function Wert=slowdown(x); if x<20 Wert=1.3; elseif x<34 Wert=0.95; elseif x<45 Wert=0.4; elseif x<100 Wert=0.14; elseif x<200 Wert=0.29; elseif x<300 Wert=0.4; elseif x<377 Wert=0.2; elseif x<420 Wert=0.4; else Wert=0.19; endif endfunction
Nun bauen wir die Werte in unsere Slowdown-Funktion ein.
for i=length (zeit) Faktor_slowdown(i)=slowdown(i); endfor r=1;
Im Anschluss definieren wir jetzt noch unsere Funktion des DGL-Systems und lösen dieses wie zuvor auch numerisch mittels Octave.
f=@(y,x) [-Infektionsrate*slowdown(x)*y(1)*y(2)/(Kapazitaet*r); +Infektionsrate*slowdown(x)*y(1)*y(2)/Kapazitaet-Genesungsrate*y(2); +Genesungsrate*y(2)-Todesrate*y(2)]; y=lsode(f, yo, zeit);
Wir stellen nun erneut unsere realen Daten vom RKI mit unserem modifizierten SRI-Modell, das nun auch die Slowdown-Funktion berücksichtigt, dar. figure(666)
plot (zeitA, AlleInfizierte./1000, '*c', zeitA,aktuelleFaelle/1000, '*r' , zeitA,AlleGenesene/1000,'*g', zeit, y (:,2),'r-', zeit, y (:,3), 'g-', zeit, y (:,3)+ y (:,2),'c-')
title ('Vergleich RKI mit Model')
xlabel ('Tage ab dem 26. Februar')
ylabel ('Zahlen in Tausend')
legend ( "kumulierte Infizierte (RKI)" ,"aktuell Infizierte (RKI)","genesen/imun (RKI)" , "Infizierte (Model)", "Genesene (Model)", "kumulierte Inzizierte (Model)", "location", "north")
grid on
axis([0,n,0,3600])
Innerhalb dieser Abbildung lässt sich schon gut erkennen, dass wir mit Hilfe der Slowdown-Funktion unser modifziertes SIR-Modell gut zu unseren aktuellen Daten des RKIs anpassen konnten. Zur weiteren Verdeutlichung folgt die Betrachtung eines kleineren Zeitausschnittes.
Aufgabe 4: Berücksichtigung der Impfungen
[Bearbeiten]Um die Impfungen berücksichtigen zu können werden zu Beginn die offiziellen Impfdaten der Bundesregierung in einer neuen Funktion impfData gesammelt. Wir plotten die Funktion impfData und starten mit Tag 300 nach dem 26.02.2020, da die Impfkampagne erst zum Jahreswechsel gestartet ist.
B=impfData();
neueGeimpfte=B(1,:);
n=length(neueGeimpfte);
zeit=[0:1:n-1];
figure(100)
plot (zeit, neueGeimpfte, 'c-')
title ('taeglich (Erst) Geimpfte in Deutschland, Quelle RKI')
xlabel ('Tage ab dem 26. Februar')
ylabel ('Personen')
legend ( "taeglich Geimpfte")
grid on
axis([300,n, 0 ,1100000])
Die Anzahl der kumulierten Impfungen plotten wir separat wie folgt.
C=impfDataGesamt();
impfungeninsgesamt=C(1,:);
n=length(impfungeninsgesamt);
zeit=[0:1:n-1];
figure(1000)
plot (zeit, impfungeninsgesamt, 'c-')
title ('insgesamt geimpfte in Deutschland, Quelle RKI')
xlabel ('Tage ab dem 26. Februar')
ylabel ('Personen')
legend ( "gesamt Geimpfte")
grid on
axis([300,n, 0 ,35000000])
Nun soll im nächsten Schritt überprüft werden, welchen Effekt die durchgeführten Impfungen auf die Gruppe der Empfänglichen hat. Hierfür wird zuerst die Kurve der Empfänglichen ohne Impfungen mit der Kurve der Empfänglichen unter Berücksichtigung der Impfungen verglichen. Wir gehen dabei davon aus, dass Geimpfte sich nicht mehr infizieren. Weiterhin vereinfachen wir unser Modell wie folgt.
- -Es werden nur die Erstimpfungen betrachtet, da diese bereits zu einem Schutz führt. Zudem gibt es auch einen Impfstoff, Johnson & Johnson, der nur eine Dosis benötigt.
- -Wir gehen davon aus, dass 5% der neuen geimpften Personen bereits eine Infektion hinter sich hatten und somit nicht zweimal von der Gruppe der Empfänglichen abgezogen werden.
- -Wir berechnen die Wirksamkeit der Impfung mit 90%, d.h. dass bei nur 10% der Geimpften kein ausreichender Schutz gegen eine mögliche Infektion besteht - die Impfwirksamkeit beträgt 0.9. Diese Personen werden folglich nicht von der Gruppe der Empfänglichen abgezogen, da sie infiziert werden können. Diese nun beschlossenen Annahmen implementieren wir in eine neue Matrix.
I=MatrixZuNummer4(); Bevoelkerung=I(1,:); % die erste Zeile der Matrix wird "Bevoelkerung" genannt, Einträge immer 83000 Infizierte=I(2,:); % die zweite Zeile der Matrix wird "Infizierte" genannt Impfungen=I(3,:); % die dritte Zeile der Matrix wird "Impfungen" genannt n=length(Bevoelkerung); % gibt mir die Länge der Zeile innerhalb der Matrix an zeit=[0:1:n-1]; Impfwirksamkeit=0.9; Empfaengliche=Bevoelkerung-(Infizierte/1000); EmpfaenglicheMitImpfung=Bevoelkerung-(Infizierte/1000)-(Impfungen/1000)*Impfwirksamkeit;
Anschließend plotten wir neben der Bevölkerung nun beide Kurven - die Empfänglichen ohne Impfung bzw. die Empfänglichen unter Berücksichtigung der Impfungen.
figure(2322)
plot (zeit, Empfaengliche, 'g-', zeit,EmpfaenglicheMitImpfung, 'r-', zeit, Bevoelkerung, 'b-')
title (['Anzahl der Empfaenglichen. Wirksamkeit der Impfung = ' num2str(Impfwirksamkeit)])
xlabel ('Tage ab dem 26. Februar')
ylabel ('Zahlen in Tausend')
legend ( "Empfaenglich ohne Impfungen" ,"Empfaenglich inkl. Impfung", "Bevoelkerung", "location", "west")
grid on
axis([0 , n , 0 , 90000]
Die blaue Gerade stellt die gesamte Bevölkerung dar. Die grüne Kurve zeigt die Personen ohne Impfungen an, die somit zur Gruppe der Empfänglichen angehören (Bevölkerung abzüglich Infizierter). Die rote Kurve beschreibt die Empfänglichen unter Berücksichtigung der Impfungen. Folglich fällt die rote Kurve relativ rasch mit dem Start der Impfkampagne um Tag 300. Man erkennt sehr deutlich, dass es ohne Impfungen sehr lange dauern würde, um eine Herdenimmunität zu erreichen. Durch die Impfungen fällt die Anzahl der potentiell Empfänglich stark, sodass noch innerhalb dieses Jahres, unter Voraussetzung, dass die Impfquote konstant bleibt und die Mutanten nicht gegen die Impfstoffe resistent sind, keiner mehr für das Virus Empfänglich sein dürfte. Die unterschiedlichen Wirksamkeiten der Impfungen haben wir zusätzlich in der nachfolgenden Animation veranschaulicht. Eine Wirksamkeit von 100& entspricht dabei, dass jeder Geimpfte vollständig aus der Gruppe der Empfänglichen entfernt wird. Eine Wirksamkeit von 0% bedeutet dagegen, dass jeder Geimpfte weiterhin in der Gruppe der Empfänglichen bleibt, bis nach einer Infektion die Gruppe hin zu den Infizierten gewechselt wird.
Mittels einer Regressionsanalyse in Excle konnten wir eine Exponential-Funktion erstellen, die eine Annäherung an die Daten der RKI-Impfzahlen ist. Unter der Annahme, dass das Impftempo so weitergeht, könnten wir mir dieser Gleichung berechnen, wann alle 83 Millionen Deutsche Geimpft sind (bzw 55 Millionen für die Kapazitätsgrenze). Nachfolgender Code implementiert hierbei unsere Impffunktion mit exponentiellen Wachstum.
Zeit=[0:1:600];
ImpfFunk= 16.76485018141*exp(0.0330771067*(Zeit-2));
C=impfDataGesamt();
impfungeninsgesamt=C(1,:);
n=length(impfungeninsgesamt);
zeit=[0:1:n-1];
figure(1001)
plot (Zeit, ImpfFunk, 'b-', zeit, impfungeninsgesamt, 'g*')
title ('Impffunktion')
xlabel ('Tage ab dem 26. Februar')
ylabel ('Personen')
legend ( "Impf-Funktion", "gesamte Impfungen (Quelle RKI)")
grid on
axis([ 0 ,600, 0 ,83000000])
Würde in dem aktuellen Tempo weitergeimpft werden, so sind auf Grund des exponentiellen Wachstums ziemlich bald alle 83 Millionen Bürger geimpft. Dabei vernachlässigen wir in dieser Annahme aber zwei Fehler:
- 1: Die Impffunktion wird irgendwann von dem exponentiellen Wachstum zu einer logistischen Funktion wechseln, da die Kapazität beschränkt ist.
- 2: Es wird hierbei davon ausgegangen, dass alle Personen der Bevölkerung geimpft werden. Dabei steht aber das Impfen der Kinder bis 16 Jahren noch zur Debatte und ebenso lässt es sich bezweifeln, ob sich jede erwachsene Person impfen lässt, bzw. ist dies gesundheitlich zum Teil auch nicht möglich (schwangere Personen).
Um deshalb nun unser Modell zu optimieren gehen wir von einer Kapazitätsgrenze von 70 Millionen aus. Damit schaffen wir die Basis für unsere nun logistische Funktion mit einem beschränkten Wachstum. Es gilt nun für die Gleichung der Impfung folgende Implementierung.
Zeit=[0:1:600]; ImpfFunkLogistisch = (70001*((1+70000*exp(-0.0317*(Zeit-100))).^-1))*1000;
Den Rest des Codes erhalten wir analog zur obigen Vorgehensweise.
C=impfDataGesamt();
impfungeninsgesamt=C(1,:);
n=length(impfungeninsgesamt);
zeit=[0:1:n-1];
figure(1001)
plot (zeit, impfungeninsgesamt, 'g*', Zeit, ImpfFunkLogistisch, 'b-')
title ('Impffunktion')
xlabel ('Tage ab dem 26. Februar')
ylabel ('Personen')
legend ( "gesamte Impfungen (Quelle RKI)", "logistische Impf-Funktion")
grid on
axis([ 250 ,600, 0 ,83000000])
Innerhalb dieser Abbildung stellen die grünen Sternchen unsere tatsächlichen realen Impfzahlen dar. Die blaue Kurve ist nun obige implementierte logistische Funktion. Es fällt auf, dass die Werte bis zum heutigen Tag sehr gut durch diese logistische Funktion approximiert wird und folglich sich der zukünftige Verlauf hierdurch ebenfalls gut approximieren lassen kann. Demnach ist davon auszugehen, dass bis zum Tag 550, was dem 29.08.2021 entspricht, jeder Impfwillige geimpft wurde. Dies stimmt auch gut mit der Einschätzung der Bundesregierung überein, die allen Impfwilligen bis zum Ende dieses Sommers geimpft haben will.
Tutorium 4 - Finite Differenzen Methode (Neumann und Dirichlet)
[Bearbeiten]Die FDM ist ein numerisches Diskretisierungsverfahren für partielle Differentialgleichungen. Es basiert darauf, dass die unbekannte Funktion auf endlich vielen Gitterpunkte approximiert wird (Gitter-basiertes Verfahren). Die Ableitungen werden durch die Differenzenquotienten näherungsweise bestimmt und ersetzt.
Taylorpolynom
Die Differenzenquotienten ergeben sich aus der Taylorentwicklung (approximation der Ableitungen nach Abbruch der Taylorreihe) für den Punkt x+h um den Entwicklungspunkt x.
.
Erster Differenzenquotient (Approximierung der 1. Ableitung)
[Bearbeiten]
vorwärts-Differenzenquotient
,
rückwärts-Differenzenquotient
,
zentralen-Differenzenquotient
Zweiter Differenzenquotient (Approximierung der 2. Ableitung)
[Bearbeiten]zweite Ableitung an der Stelle (falls hinreichend oft differenzierbar)
Die Formel für ergibt sich aus der Differenz der ersten Differenzenquotienten
mithilfe der Taylorentwicklung bis zur vierten Ableitung:
Randwertproblem
[Bearbeiten]Es soll die Diffusion auf einem beschränkten Gebiet betrachtet werden. Dafür ist es hilfreich, sich anzuschauen, wie sich die Funktion auf dem Rand des Gebietes verhält. Bei einer Randwertaufgabe sind diese durch Bedingungen festgelegt. In dieser Aufgabe wird die schon bekannte stationäre Poisson-Gleichung betrachtet.
Dirichlet Randwertproblem
[Bearbeiten]Ist die gesuchte Funktion am Rand durch eine gegebene Funktion festgelegt , erfüllt die Dirichlet Randbedingung:
Neumann Randwertproblem
[Bearbeiten]Sind die Richtungsableitungen der Funktion in der Richtung des äußeren Normalenvektors gegeben,
erfüllt die Neumann Randbedingung:
Randwertproblem im Eindimensionalen (1D)
[Bearbeiten]Dirichletproblem (1D)
[Bearbeiten]Sei . Gesucht werden Näherungen für die Funktionswerte auf dem äquidistanten Gitter
G=
die Werte am Rand sind bekannt (Randbedingungen ).
Die zweiten Ableitungen der Funktionswerte werden mit dem zweiten Differenzenquotienten diskretisiert.
Es ergibt sich folgendes lineares Gleichungsystem:
mit einer tridiagonaler Systemmatrix
und der rechten Seite des Systems , bei der die Anfangsbedingungen eingebaut sind.
Neumannproblem (1D)
[Bearbeiten]In diesem Fall sind die Ableitungen in die Normalenrichtungen :
gegeben. Um die Ableitungen in den Randpunkten zu approximieren, führen wir neue Unbekannte ein.
Für die Approximation der Ableitung an den Rändern gilt:,
- vorwärts Differenzenquotient
- rückwärts Differenzenquotient
Für die neuen Unbekannten die 0-te und die - te Gleichung angeben, gilt:
,
.
Randwertproblem im Zweidimensionalen (2D)
[Bearbeiten]Dirichletproblem (2D)
[Bearbeiten]Dieser Teil umfasst den ersten Teil der Aufgabe. Es wird die stationäre Poisson-Gleichung betrachtet, für die die Dirichlet-Randbedingungen erfüllt sein sollen.
Quelldichtefunktion
Zuerst wird eine Quelldichtefunktion der Poisson-Gleichung definiert:
function wert=Quellfunktion(x,y)
if sqrt((x.-3.25).^2+(y.-3).^2)<=0.35 wert=1;
else wert=0;
endif
endfunction
Festlegen des Gebietes D
Nun wird ein Gebiet D festgelegt. Dazu wird ein äquidistantes Gitter definiert.
Ziel ist es, die Funktionswerte der unbekannten Funktion in all diesen Gitterpunkten zu finden. ui,j:≈u(xi,y:j)
xend=10; %Endpunkt in x-Richtung yend=8; %Endpunkt in y-Richtung N=60; %Anzahl der Punkte in x-Richtung hx=xend/(N+1); %Schrittweite in x-Rictung hy=hx; %gleiche Schrittweite in y-Richtung M=floor(yend/hy)-1; %Anzahl der Punkte in y-Richtung h=hx; %Schrittweite in beide Richtungen identisch [x,y]=meshgrid(hx:hx:xend-hx,hy:hy:yend-hy); % Der 0-te und N+1 -te Index entsprechen den Rändern und gehören somit nicht zum Gitter. diff=1; %konstanter Diffusionskoeffizient
Wir haben ein Gitter 60x47 (NxM) erstellt.
Randbedingungen
Bei einem Dirichlet Randwertproblem wird die gesuchte Funktion am Rand durch eine Funktion gestgelegt, die allerdings hier für die 4 Ränder konstante Werte annehmen soll.
unten=0.025; oben=0.125; links=-0.125; rechts=0.025;
Systemmatrix
Da wir uns im zweidimensionalen Raum bewegen, müssen wir die zweiten Ableitungen in beide Raumrichtungen beachten. Diese lassen sich jeweils durch den zweiten Differenzenquotienten approximieren.
,
Die zweiten Differenzenquotienten approximieren die zweiten partiellen Ableitungen jeweils in den Richtungen x und y in jedem Gitterpunkt .
Aufgrund der Definition des Laplace-Operators müssen die beiden addiert werden und somit ergibt sich folgendes Approximationsschema:
Um die Systemmatrix aufstellen zu können, müssen die Werte der unbekannten Funktion für all Gitterpunkte sowie die Funktionswerte der Funktion der rechten Seite in eine langen Vektor eingeordnet werden (Assemblierung).
Daraus ergibt sich ein lineares Gleichungssystem mit Aufbau der Systemmatrix
mit Diagonalblock
und der Einheitsmatrix auf der Nebendiagonale.
%Tridiagonale Matrix Matrix1=zeros(N); Matrix1=Matrix1-4*eye(N); Matrix1=Matrix1+diag(ones(N-1,1),1); Matrix1=Matrix1+diag(ones(N-1,1),-1); %Einheitsmatrix Matrix2=eye(N); %Erstellung der Systemmatrix Ah=zeros(N*M); %Einsetzen der Blöcke an die passenden Stellen for i=1:M Ah(N*(i-1)+1:i*N,N*(i-1)+1:i*N)=Matrix1; endfor for i=2:M Ah(N*(i-2)+1:N*(i-1),N*(i-1)+1:N*i)=Matrix2; endfor for i=2:M Ah(N*(i-1)+1:N*i,N*(i-2)+1:N*(i-1))=Matrix2; endfor Ah=(-diff/h^2)*Ah; %Einberechnung des Vorfaktors der Systemmatrix
Funktion g der rechten Seite
Zur Aufstellung der rechten Seite wird zunächst die Quellfunktion für jeden Gitterpunkt eingespeichert und danach die Dirichlet-Randbedingungen hinzugefügt.
for i=1:N
for j=1:M
f(j,i)=1*Quellfunktion(x(j,i),y(j,i));
%Dirichlet Randbedingung unten und oben: %Erläuterung: == Zeichen ist eine Abfrage. = Zeichen ist eine Zuweisung
if j==1 f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+unten*k_diff/h^2; endif
if j==M f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+oben*k_diff/h^2; endif
%Dirichlet Randbedingung links und rechts:
if i==1 f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+links*k_diff/h^2; endif
if i==N f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+rechts*k_diff/h^2; endif
endfor
endfor
%Betrachtung der Ecken: Diese Einträge werden dabei gesondert betrachtet, da an ihnen zwei Randbedingungen zusammentreffen.
f(1,1)=Quellfunktion(x(1,1),y(1,1))+(k_diff/h^2)*(links+unten);
f(1,N)=Quellfunktion(x(1,N),y(1,N))+(k_diff/h^2)*(rechts+unten);
f(M,1)=Quellfunktion(x(M,1),y(M,1))+(k_diff/h^2)*(links+oben);
f(M,N)=Quellfunktion(x(M,N),y(M,N))+(k_diff/h^2)*(rechts+oben);
Die Funktion wird nun in einen langen Vektor b eingeordnet. Da der "reshape"-Befehl spaltenweise anordnen würde, wir aber zeilenweise anordnen wollen, muss die Matrix der Funktion vor der Einordnung transponiert werden. Der Vorfaktor −1 wird durch den Aufbau der Poisson-Gleichung −Δu=g bedingt.
b=-1*reshape(f',N*M,1); %Muss transporniert werden, damit die Zeilen untereinander aufgestellt werden
Lösen des linearen Gleichungssystems und grafische Darstellung
Im letzten Schritt wird das lineare Gleichungssystem zur Ermittlung der unbekannten Funktion gelöst. Zu beachten ist dabei, dass nach dem Umordnen des Vektors in eine N × M -Matrix noch transponiert werden muss, damit eine M x N-Matrix entsteht, die die Werte der Funktion den passenden Gitterpunkten zuordnet.
Loesung=Ah\b; Loesung_matrix=reshape(Loesung,N,M);% Matrix mit N(Zeilen)x M(Spalten) Loesung_matrix=Loesung_matrix'; % Rücktransponierung nach reshape
Neumannproblem (2D)
[Bearbeiten]Quelldichtefunktion und Festlegung des Gebiets D
Analog zu Dirichlet (2D) - Gleicher Code
Randbedinungen
Seien die Ableitungen der unbekannten Funktion in den Randpunkten des Rechtecks gegeben:
- linker Rand:
- rechter Rand:
- unterer Rand:
- oberer Rand:
Die Neumann-Randbedingungen werdem im Folgenden jedoch als homogen angesehen, also gilt α=β=γ=δ=0.
Bei der Anwendung der einseitigen Differenzenquotienten muss der Vektor den Unbekannten um die Randwerte erweitert werden,
diese werden zur Bildung der Differenzenquotienten verwendet:
- linker Rand: den vorwärts -Differenzenquotient
- rechter Rand: den rückwärts -Differenzenquotient
- unterer Rand: den vorwärts -Differenzenquotient
- oberer Rand: den rückwärts -Differenzenquotient
%Erweitern der Blockmatrizen um 2 Einträge wegen Neumann-Randbedingungen [x,y]=meshgrid(0:h_x:x_end,0:h_y:y_end); N1=N+2; M1=M+2;
Randbedingungen und Systemmatrix
In dieser Modellierung werden die Neumann-Randbedingungen auf dem linken und rechten Rand angenommen (diese sind homogen). Auf dem oberen und unteren Rand gelten Dirichlet-Randbedingungen.
%Festlegen der Randbedingungen %links und rechts homogene Neumann-Randbedingungen %oben und unten Dirichlet-Randbedingungen unten=-0.09; oben=0.03;
%Zunächst Erstellen der einzelnen Blöcke %Tridiagonale Matrix Matrix1=zeros(N1); Matrix1=Matrix1-4*eye(N1); Matrix1=Matrix1+diag(ones(N1-1,1),1); Matrix1=Matrix1+diag(ones(N1-1,1),-1); Matrix1(1,1)=Matrix1(N1,N1)=h; Matrix1(1,2)=Matrix1(N1,N1-1)=-h; %erweiterte Einheitsmatrix (Null Oben Links und unten Rechts) Matrix2=eye(N1); Matrix2(1,1)=Matrix2(N1,N1)=0; %Erstellung der Systemmatrix Ah=zeros(N1*M1); %Einsetzen der Blöcke for i=1:M1 Ah(N1*(i-1)+1:i*N1,N1*(i-1)+1:i*N1)=Matrix1; endfor for i=1:M1-1 Ah(i*N1+1:(i+1)*N1,(i-1)*N1+1:i*N1)=Matrix2; Ah((i-1)*N1+1:i*N1,i*N1+1:(i+1)*N1)=Matrix2; endfor
Würden die Neumann-Randbedingungen auf dem oberen und unteren Rand angenommen werden, so müsste die Systemmatrix Ah angepasst werden. In diesem Fall würde in der ersten Blockzeile die erste Blockspalte durch eine h -Diagonalmatrix ersetzt werden und die zweite Blockspalte durch eine −h -Diagonalmatrix. In der letzten Blockzeile würde diese Ersetzung in der letzten Blockspalte ( h -Diagonalmatrix) und in der vorletzten Blockspalte ( −h -Diagonalmatrix) stattfinden. Siehe Bild:

Funktion f der rechten Seite
Auch hier wird die Quelldichtefunktion in den Gitterpunkten gespeichert, wobei die Dirichlet-Randbedingungen beachtet werden müssen. Aufgrund der homogenen Neumann-Randbedingungen addieren sich am linken und rechten Rand sowie an den Eckeinträgen keine zusätzlichen Bedingungen hinzu.
for j=1:M1
for i=1:N1
f(j,i)=Quellfunktion(x(j,i),y(j,i)); %innere Punkte ohne Randberührung
if j==1
f(j,i)=Quellfunktion(x(j,i),y(j,i))+unten*diff/h^2; %Dirichlet am unteren Rand
endif
if j==M1
f(j,i)=Quellfunktion(x(j,i),y(j,i))+oben*diff/h^2; %Dirichlet am oberen Rand
endif
endfor
endfor
%links und rechts wie innen berechnet, da Neumann-Randbedingugnen hier homogen sind
%Festlegen der Eckeneinträge
%da an allen Ecken Neumann gilt, fallen hier die Dirichlet-Bedingungen weg
f(1,1)=Quellfunktion(x(1,1),y(1,1));
f(1,N1)=Quellfunktion(x(1,N1),y(1,N1));
f(M1,1)=Quellfunktion(x(M1,1),y(M1,1));
f(M1,N1)=Quellfunktion(x(M1,N1),y(M1,N1));
%reshape-Befehl zum Anordnen von f in einen langen Vektor, dafür muss f transponiert werden, damit zeilenweise angeordnet wird
b=-1*reshape(f',N1*M1,1); %Vorfaktor -1 kommt durch den Aufbau der Poisson-Gleichung
Lösen des linearen Gleichungssystems und grafische Darstellung
Das Vorgehen zum linearen Gleichungssystems ist analog zu dem bei den Dirichlet-Randwertproblemen (gleicher Code)
Fazit
[Bearbeiten]Ziel dieser Tutoriumsaufgabe war es, mit Hilfe der Finiten-Differenzen-Methode eine Lösung für unsere unbekannte Dichtefunktion herzuleiten. Weil eine analytische Bestimmung der Lösung (wie in Tutoriumsaufgabe 2 dargestellt) sehr komplex und schwer zu finden ist, haben wir in dieser Aufgabe auf eine numerische Herleitung zurück gegriffen. Dies bildete gleichzeitig den Übergang von der kontinuierlichen Modellierung hin zur diskreten Modellierung. Denn es wurde aus einer unbekannten Funktion mit reellem Definitionsbereich (kontinuierlich) eine Approximation in endlich vielen Gitterpunkten (diskret). Die räumliche Diffusion findet dabei ausschließlich in Bezug auf die benachbarten Gitterpunkten statt (was an unserer Systemmatrix mit dem bekannten Stern-Schema liegt). Eine Krankheit kann sich also nur auf den linken, rechten, unteren oder oberen Nachbarn ausweiten. Dies unterscheidet dieses Modell mit unserem Modell aus der diskreten Modellierung, wo der Austausch der Krankheit durch eine Transportmatrix auch in Zellen möglich ist, die nicht an die eigentliche Zelle grenzen.
Ausblick
[Bearbeiten]In Tutoriumsaufgabe 3 wurde das SIR-Modell betrachtet, welches die zeitliche Dynamik der Populationsdynamik widerspiegelt. In Tutoriumsaufgabe 4 wurde dagegen die räumliche Verbreitung mittels der Finite-Differenzen-Methode dargestellt. Beide Teile sollen nun in einer finalen Tutoriumsaufgabe miteinander verknüpft werden. Es entsteht die Reaktionsdiffusiongleichung, in der sowohl räumliche, als auch zeitliche Aspekte in einem Modell dargestellt werden.
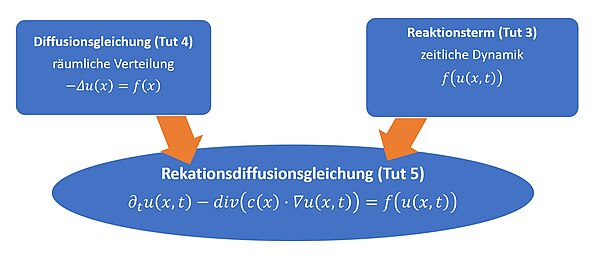
Tutorium 5 und Theorie SW 10 - Numerische Diskretisierung der Reaktionsdiffusionsgleichung mit FDM
[Bearbeiten]
I. räumliche Diskretisierung der hom. Diffusionsgleichung (linke Seite)
[Bearbeiten]
II. räumliche Diskretisierung der Reaktionsdiffusionsgleichung (rechte Seite)
[Bearbeiten]Nachdem wir gerade die linkte Seite diskretisiert haben, folgt nun die rechte Seite.

IIII. Zeit-Diskretisierung der Reaktionsdiffusionsgleichung
[Bearbeiten]IV. Räumliche Diskretisierung des regionaldifferenzierten Diffusionskoffizienten
[Bearbeiten]Annimationen aus dem Code: Teilaufgabe a) (Implementierung des FDM-Verfahrens zur Lösung der Reaktionsdiffusionsgleichung)
[Bearbeiten]Unterschiedliche Startwerte
[Bearbeiten]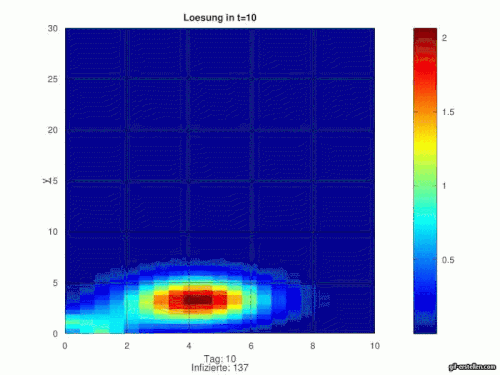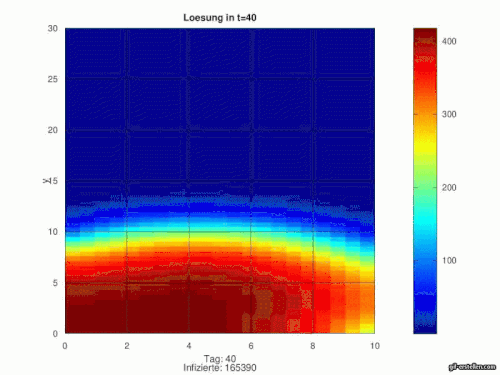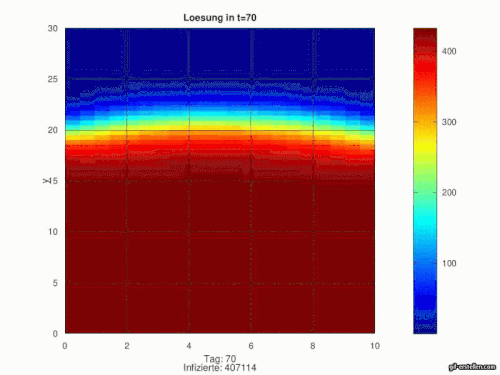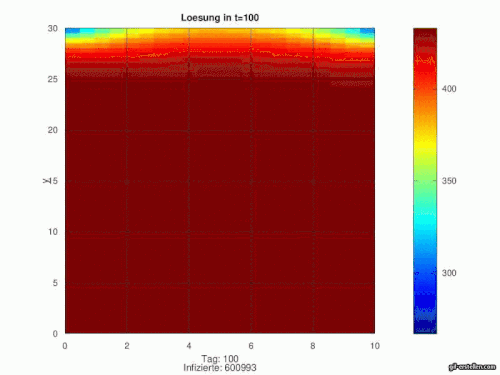
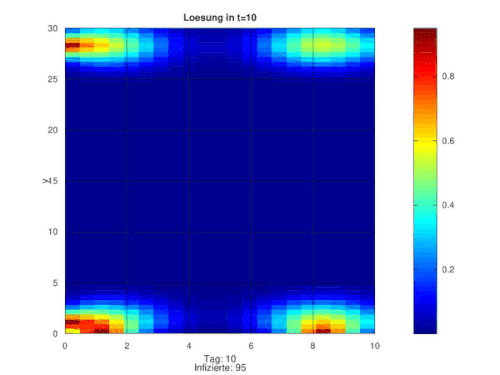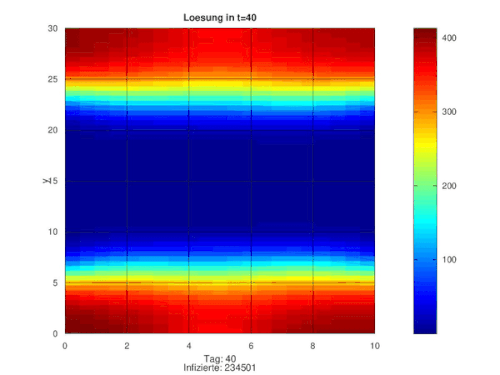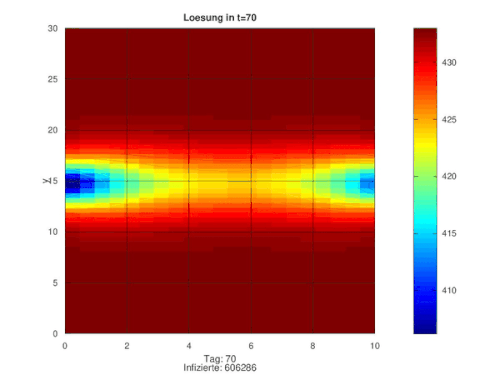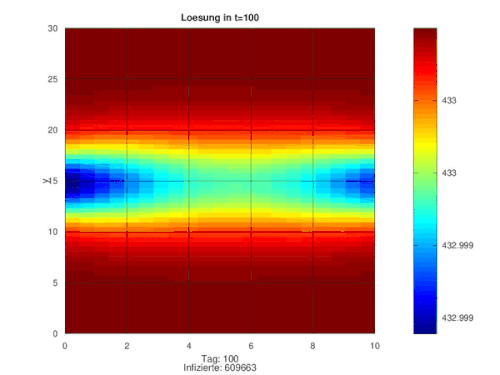
Die zwei Grafiken geben das Infektionsgeschehen bei unterschiedlicher Anfangsverteilung an. Links gibt es zu Beginn zwei Hotspot links unten des Landes. Rechts gibt es 4 Hotspots, verteilt in den Ecken.
Dann breitet sich die Intektion über das Land aus, wie man in den Grafiken sieht.
Links "verschmelzen" die Start-Hotspots schnell zu einem, von dort verbreitet sich die Infektion.
Vergleich: Wir vergleichen Tag 70 der beiden Startwerten:
Startwert links: 323.000 Infizierte
Startwert rechts: 400.000 Infizierte
Unterschiedliche Infetkionsrate
[Bearbeiten]Wir setzten im Vergleich zu oben links die Infektionsrate höher auf 0,6
Das Resultat ist nicht sehr überraschend: Wir sehen, dass die Infektion viel schneller über das ganze Land verbteitet wird als in der 1. Grafik.
In den Letzten 2 Zeitschritten geschieht fast gar nichts mehr, da schon fast alle Menschen Infiziert sind.
Teilaufgabe b) Einarbeitung von Slowdown und Impfung
[Bearbeiten]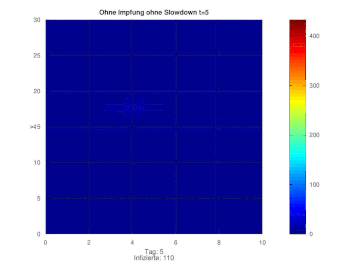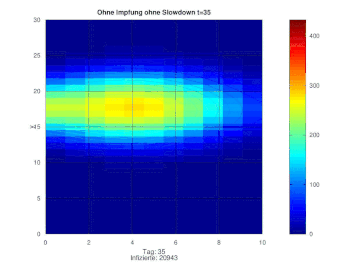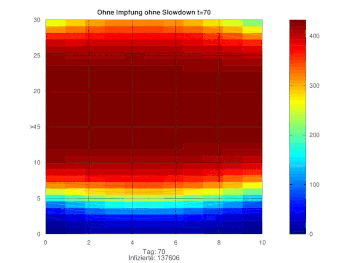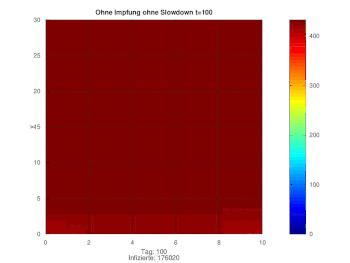


Im letzten Bild wurde eine andauernde, lineare Impfung eingebaut (=tägich gleich viele Impfungen, bedeutet die Anzahl der Bevölkerung wird in jedem Schritt um einen Konstanten Wert gesenkt)
Teilaufgabe c) (Erweiterung der räumlichen Epidemieausbreitung in Abhängigkeit der Populationsdichte)
[Bearbeiten]Wir verwenden nun nicht mehr eine konstante Bevölkerungsdichte, sondern "kreieren" Großstädte und Dörfer. Diese Verteilung hat Auswirkungen auf das Infektionsgeschehen.
Die Befölkerungsstrucktur sieht folgendermaßen aus:

Der Verlauf der Pandemie lässt sich so abbilden.

Interpretation:
Tutorium 6: Reaktionsdiffussionsprozess ergänzt um Transportwege (Flugnetzt + Reaktion-Diffusion)
[Bearbeiten](Diese Modellierung ist ein Versuch. Keine Garantie, dass es stimmt oder Sinn ergibt)
Es sollte versucht werden, den epidemiologisch Reaktions-Diffusionsprozess dahingehend zu verändern, dass zusätzlich zu den "Ansteckungen der Nachbarn", auch Transortwege stattfinden. Somit soll die Infektion an weit entfernte Orte gebracht werden, von wo sich die Infektion dann auch weiter verbreiten kann.
Unterschied zu Tutorium 5: dort waren keine "Sprünge" der Orte möglich. Die Infektion verbreitete sich stets von Ort zu Ort.
Ansatz dieser Überlegung war das Sternschema. Aus diesem ergibt sich bekanntlich, dass ein Gitterpunkt u(i,j) mit seinen Nachbarn rechts links oben und unten in Verbindung steht.
Nun soll die Systemmatrix dahingehend abgeändert werden, dass dieser eine Gitterpunkt u(i,j) zusätzlich zu seinen Nachbarn auch mit einem weit entfernten Gitterpunkt in Verbindung steht. Dazu muss man lediglich in der entsprechenden Zeile/Spalte der Systemmatrix einen Wert von 0 abändern.
Das gerade beschriebene wurde in folgendem Bild versucht darzustellen.
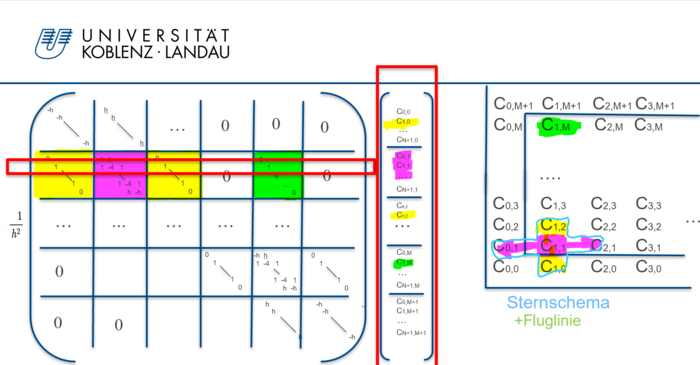
Der grüne Block wurde im Vergleich zur ursprünglichen Systemmatrix leicht verändert. Dadurch steht u(1,1) nicht mehr nur mit seinen Nachbarn in Verbindung (Sternschema) sondern auch mit u(1,M). Dies erkennt man, in dem man "Zeile x Spalte" rechnet.
Nun wurde dieses Vorgehen in Octave implementiert. Dazu wurde ein 10X10 Gitter erstellt, und anschließend analog wie in Tutorium 5 der Code ausgeführt. Lediglich die Systemmatrix wurde an einzelnen Punkten durch einen Eintrag ungleich 0 geändert.
Ausgangssituation
Wir kreieren einen einzelnen Hotspot um den den Gitterpunkt (4/2) herum.

Unser Flughafen befindet sich nicht so weit weg im Punkt (2/2). Von dort gibt es 2 Flugnetze an weit entfernte Punkte. Im Startpunkt t0 ist in dem Flughafengebiet (2/2) noch keine Infektion, deshalb sieht man den Transportprozess noch nicht (nur gesunde reisen) Die Infektion verbreitet sich nun aber vom Hotspot (4/2) relativ schnell zum Ort des Flughafens. Erreicht die Infektion diesen Punkt, "fliegen" auch Infizierte quer durchs Land zu den vorher definierten Punkten. An dem Zielflughafen verbreitet sich nun ebenfalls die Infektion.
Wir haben dieses Vorgehen einmal mit einer Flugverbindung modelliert, und ein zweites mal mit 2 verschiedenen Zielflughäfen modelliert.
Ergänzungen Octave-Tutorial
[Bearbeiten]Diese Ergänzungen wurden bei dem Octave-Tutorial vorgenommen, um die Implementation der Gruppe bzgl. der verwendeten Octave-Befehle nachvollziehbar zu machen.
- Matrix-Multiplikation in Octave - notwendig für die Modellierung diskreter Transportprozesse.
Skripte in Octave
[Bearbeiten]Referenzieren Sie hier die von Ihnen verwendeten Skripte und Bibliotheken in Octave oder R/Studio
Literatur
[Bearbeiten]Zyklus 4 * letzte Anpassung Notieren Sie hier die von Ihnen verwendete Literatur







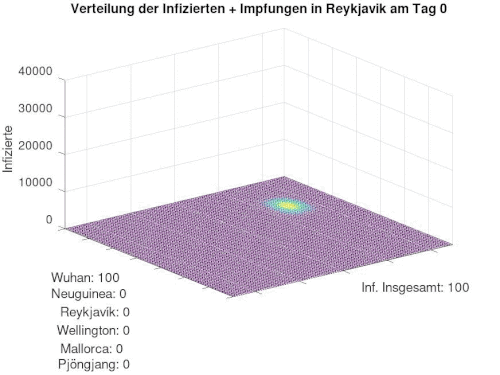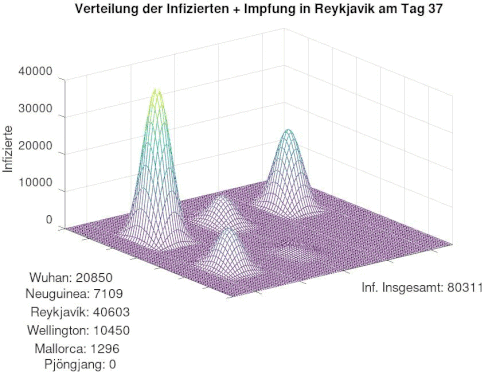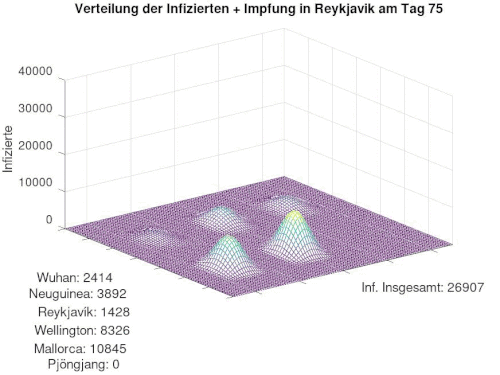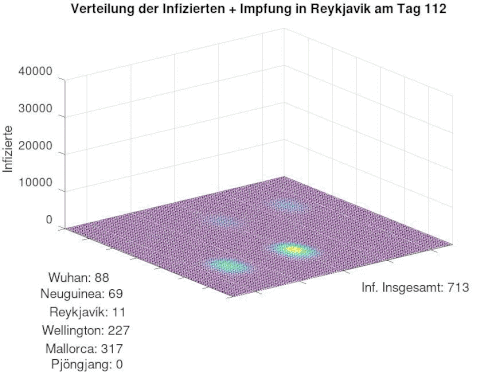






















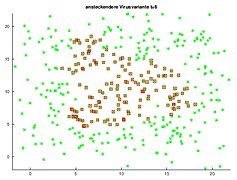

![{\displaystyle \partial _{t}u(x,t)-\partial _{x}(c(x)\partial _{x}u(x,t))=f(x,t),\ x\in [0,L]\subset \mathbb {R} \ \quad {\mbox{bzw.}}\quad \partial _{t}u(x,t)-div\ (c(x)\nabla u(x,t))=f(x,t),\ x\in \ \mathbb {R} ^{n},\ t\in \mathbb {R} ^{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a92cb2c92f2b3e8f0ad7e22c322be48a901f7e8)


![{\displaystyle x\in [0,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d35e3fa30fa9d0e9f57923fb0101848d4fea625a)




![{\displaystyle [x,x+\Delta x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3adcf4c82ed495a6478a43316b80154c95a040f5)







![{\displaystyle ([c(x)u'(x)])'=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/115ad600369591fb4cea9f1aa7951980b7cd02d2)









![{\displaystyle \partial _{t}u(x,t)-\partial _{x}(c(x)\partial _{x}u(x,t))=f(x,t),\ x\in [0,L]\subset \mathbb {R} \ \quad {\mbox{oder}}\quad \partial _{t}u(x,t)-div\ (c(x)\nabla u(x,t))=f(x,t),\ x\in \ \mathbb {R} ^{n},\ t\in \mathbb {R} ^{+}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b7d31a21c11d68430958208a765e1a760f66c42)










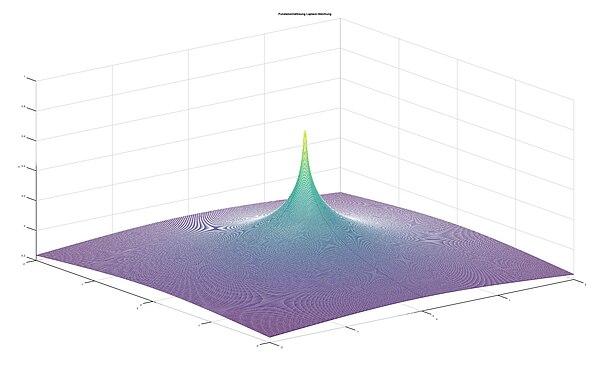





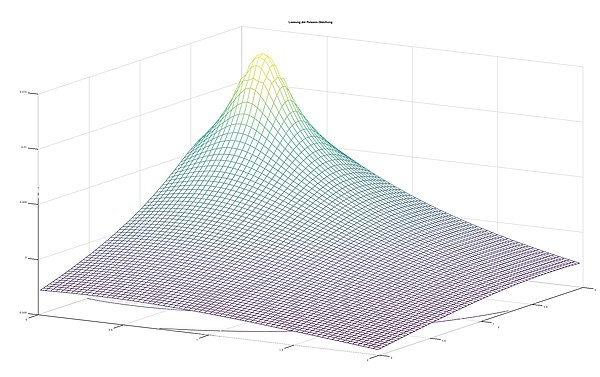


















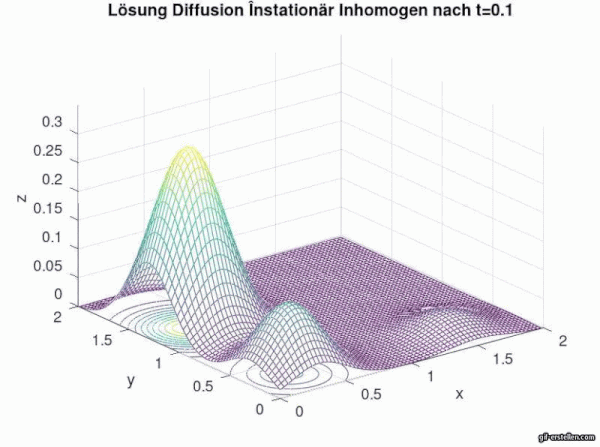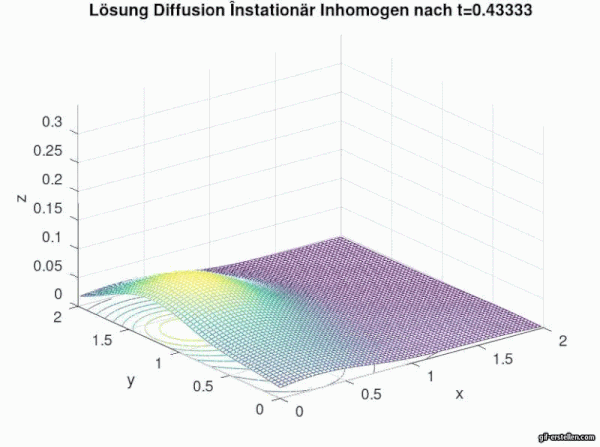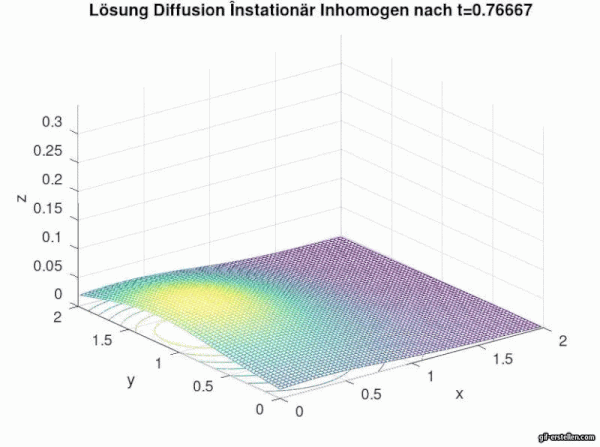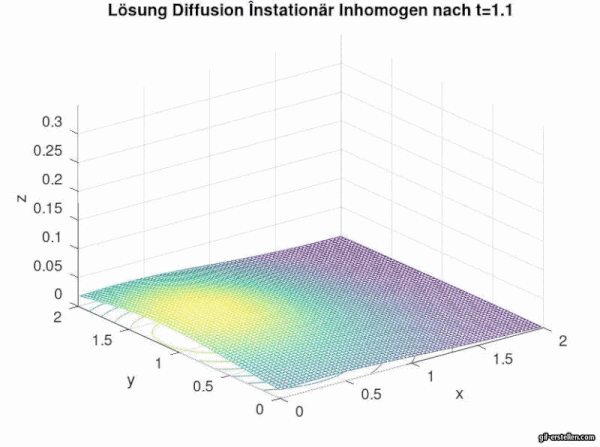











































































































![{\displaystyle x\in [a,b]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/773c4531c022eddb88d782c0a6ccd2bae7fc18fa)
![{\displaystyle \{x_{i}=a+ih,\ i=1,\ldots ,n\in \mathbb {N} \}\subset [a,b],\quad h={\frac {b-a}{n+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab4c3721e88eb097b68924849616c30ce086c07c)