Kurs:Topologische Invertierbarkeitskriterien/Polynomalgebra

Einführung

Eine Polynomalgebra $A[t]$ ist ein Vektorraum von Polynomen, wobei die Koeffizienten aus der gegebenen Algebra $A$ stammmen. Die Polynomalgebra $A[t]$ ist ein wesentliches Hilfsmittel, um eine Algebraerweiterung $B$ von $A$ zu konstruieren, in denen ein gegebenes $z\in A$ invertierbar ist, wenn es bestimmte topologische Invertierbarkeitskriterien erfüllt.

Bemerkung: Algebraerweiterung

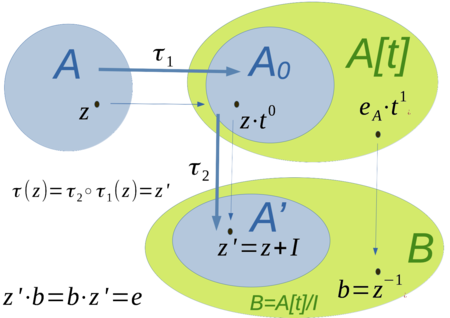
Bei der Konstruktion der Algebraerweiterung, in der ein $z\in A$ invertierbar ist, wird in einem ersten Schritt die Algebra der Polynome $A[t]$ betrachtet. Die folgende Abbildung zeigt, wie die Algebraerweiterung $B$ über die Polynomalgebra konstruiert wird.

Algebraischer Abschluss

Wir erweitern nur die Algebra $A$ um ein zusätzliches Element $t\notin A$ enthält, das in einer Algebraerweiterung $B$ von $A$ enthalten sein soll. Da die Multiplikation und die Addition in $B$ abgeschlossen sein müssen, entstehen Polynome durch Multiplikationen $a\cdot t$ und $t\cdot t=t^{2}$ mit Koeffizienten $a\in A$ n, die als Summanden $a_{n}\cdot t^{n}$ als Polynome in der Algebraerweiterung enthalten sein müssen.

Erweiterung der Algebra

Dies beinhaltet die Abgeschlossenheit der

multiplikative Verknüpfung von $t$ mit sich selbst und daher müssen auch $t^{n}$ mit $n\in \mathbb {N}$ wieder in $B$ liegen,
die beliebige multiplikative Verknüpfungen von $t^{n}\in B$ mit Elementen aus $A$ wieder in $B$ liegen, d.h. $a_{n}\cdot t^{n}\in B$ liegen.
der additive algebraische Alschluss verlangt auch schließlich, dass additive Verknüpfungen aus $a_{n}\cdot t^{n}\in B$ wieder in $B$ liegen.

Polynome mit Koeffizienten aus der gegebenen Algebra

Aus dieser Notwendigkeit betrachtet man Polynome mit Koeffizienten aus $A$ als ersten Schritt, um eine Algebraerweiterung zu konstruieren, in der ein $z$ invertierbar sein kann.

Polynomalgebra

Wir betrachten nun zu einer gegeben topologischen Algebra ${\textstyle \left(A,\left\|\cdot \right\|_{\mathcal {A}}\right)\in {\mathcal {K}}(\mathbb {K} )}$ die Menge der Polynome mit Koeffizienten in $A$ .

p(t)=\sum _{k=0}^{n}p_{k}\cdot t^{k}{\mbox{ mit }}p_{k}\in A{\mbox{ für }}k\in \{0,1,...,n\}

und Potenzreihen mit Koeffizienten in der Algebra $A$

p(t)=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ mit }}p_{k}\in A{\mbox{ für }}k\in \mathbb {N} _{o}

Grad von Polynomen

Zunächst einmal würde man Polynome formal eher in der obigen Form mit $n\in \mathbb {N} _{o}$ notieren und mit $p_{n}\not =0_{A}$ würde $n$ den Grad des Polynoms angeben. Für das Cauchyprodukt von zwei Polynomen $p,q\in A[t]$ ist diese Schreibweise allerdings ungeeignet, da bei der Addition und Multiplikation zwei Polynomen $p,q\in A[t]$ die Handhabung des Grades zusätzlichen formalen Aufwand nach sich zieht, der aber für die weitern Betrachtungen von Algebraerweiterungen keine Rolle spielt.

Schreibweise für die Polynomalgebra

Daher werden die Polynome wie folgt über "endliche" Folgen $c_{oo}(A)$ definiert, die ab einer Indexschranke $n\in \mathbb {N} _{o}$ nur noch aus dem Nullvektor $0_{A}$ in $A$ besteht.

p(t)=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ mit }}(p_{k})_{k\in \mathbb {N} _{0}}\in c_{oo}(A)

Cauchy-Produkt

Gegeben sind allgemein zwei Polynome $p,q$ mit Koeffizienten aus ${\textstyle A}$ .

p(t):=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ und }}q(t):=\sum _{k=0}^{\infty }q_{k}\cdot t^{k}

Dann wird Cauchy-Produkt von $p,q$ wie folgt definiert:

p(t)\cdot q(t):=\sum _{n=0}^{\infty }\left(\sum _{k=0}^{n}p_{k}\cdot q_{n-k}\right)t^{n}.

Bemerkung: Cauchy-Produkt

Betrachtet man Polynome $\mathbb {R} [t]$ oder $\mathbb {C} [t]$ mit reellen oder komplexwertigen Koeffizienten, so fasst das Cauchy-Produkt durch Anwendung vom Distributivgesetz, Assoziativgesetz und die Kommunitivtät der Addition die Terme bzgl. $t^{n}$ , die bei der Multiplikation den Exponenten $n$ liefert, also:

\left(p_{k}\cdot t^{n}\right)\cdot \left(q_{n-k}\cdot t^{n-k}\right)=p_{k}\cdot q_{n-k}\cdot t^{n}

Die dazu verwendeten algebraischen Operationen sind auch auf eine (topologische) Algebra übertragbar.

Bemerkung: Kommuntativtät Koeffizienten

In einer Algebra $A$ kann die Kommutativität nicht für die Koeffizienten der Polynome $p_{k}\in A$ vorausgesetzt werden. Betrachten Sie dazu die Polynomalgebra $A[t]$ mit Koeffizienten aus $A:=Mat(n\times n,\mathbb {R} )$ mit der Matrixmultiplikation als multiplikative Verknüpfung auf $A$ .

Aufgabe für Lernende

Betrachten Sie Konvexkombinationen der 3. Ordnung und erläutern Sie, warum diese mit Polynome mit Koeffizient im $\mathbb {R} ^{n}$ darstellen, wobei hier der Definitionsbereich von $t\in [0,1]$ in der Anwendung auf ein Interval konkret beschränkt wird.
Betrachten Sie die Algebra der $2\times 2$ $2\times 2$ Matrizen $A:=Mat(2\times 2,\mathbb {K} )$ $A:=Mat(2\times 2,\mathbb {K} )$ über dem Körper $\mathbb {K} =\mathbb {Q} ,\mathbb {R} ,\mathbb {C}$ $\mathbb {K} =\mathbb {Q} ,\mathbb {R} ,\mathbb {C}$ und der Matrixmultiplikation als multiplikative Verknüpfung auf $A$ $A$ .
- Welche Zusammenhänge aus der Linearen Algebra kennen Sie bzgl. Polynomen und Matrizen?
- Welche Gemeinsamkeiten und Unterschiede gibt es Sätzen in der linearen Algebra (z.B. beim charakteristischen Polynom, Satz von Cayley-Hamiliton, ...)