Kurs:Topologische Invertierbarkeitskriterien/Lemma - Kaskadenprodukte

Lemma - Kaskadenprodukte

Sei $(A,\|\cdot \|_{\mathcal {A}})$ eine unital positive topologische Algebra mit dem basiserzeugenden $p$-Gaugefunktionalsystem $\|\cdot \|_{\mathcal {A}}$, dann gibt es für alle $\alpha \in {\mathcal {A}}$ eine isotone Stetigkeitssequenz ${\textstyle \left(\left\|\cdot \right\|_{(\alpha ,n)}\right)_{n\in \mathbb {N} _{0}}}$, die folgende Eigenschaften besitzt:

• (KM1) ${\textstyle \left\|\cdot \right\|_{(\alpha ,k)}\leq \left\|\cdot \right\|_{(\alpha ,k+1)}}$ für $k\in \{1,\ldots ,n-1\}$
• (KM2) ${\textstyle \displaystyle \left\|\prod _{k=1}^{n}x_{k}\cdot y_{k}\right\|_{\alpha }\leq \prod _{k=1}^{n}\left(\left\|x_{k}\right\|_{(\alpha ,k)}\cdot \left\|y_{k}\right\|_{(\alpha ,k)}\right)}$

Beweis - Kaskadensummen

Für den Beweis verwendet man Ungleichungen für die Stetigkeit der Multiplikation für ein basiserzeugendes Gaugefunktionalsystem aus dem Topologisierungslemma für Algebren. Der Beweis erfolgt in 3 Teilen

• Stetigkeitssequenz wird induktiv definiert.
• (K1) Isotonie der Stetigkeitssequenzen
• (K2) Beweis der Kaskadenungleichung der Multiplkation

Beweis 1 - Stetigkeit der Multiplikation

Mit der Stetigkeitssequenzen kann man analog zu den Kaskadensummen über die Stetigkeit der Multiplikation erzeugen, d.h. es gibt zu jedem $p$-Gaugefunktional $\|\cdot \|_{\alpha }$ ein $\|\cdot \|_{\beta }$, ein $M_{\beta }\geq 1$ mit

$\|x\cdot y\|_{\alpha }\leq M_{\beta }\cdot \|x\|_{\beta }\cdot \|y\|_{\beta }$

Für die Stetigkeitskonstanten $M_{\beta }$ der Multiplkation bei einem basiserzeugenden $p$-Gaugefunktional gilt zunächst einmal $M_{\beta _{1}}>0$. Ohne Einschränkung kann aber $M_{\beta _{1}}\geq 1$ gewählt werden.

Beweis 2 - Stetigkeit der Multiplikation

Die induktive Definition der Stetigkeitssequenz kann erfolgt pro Index $k\in \mathbb {N}$ über zweifach über die Stetigkeit der Multiplikation erzeugen und zu jedem $p$-Gaugefunktional $\|\cdot \|_{\alpha }$ gibt es ein $p$-Gaugefunktional $\|\cdot \|_{\beta _{1}}$ und ein $M_{\beta _{1}}\geq \max\{1,\|e_{A}\|_{\beta _{1}}\}$ mit

$\|x\cdot y\|_{\alpha }\leq M_{\beta _{1}}\cdot \|x\|_{\beta _{1}}\cdot \|y\|_{\beta _{1}}\leq M_{\beta _{1}}\cdot \|x\|_{\beta _{1}}\cdot \underbrace {M_{\beta _{1}}} _{\geq 1}\cdot \|y\|_{\beta _{1}}$

für alle $x,y\in A$. Zu $\beta _{1}\in {\mathcal {A}}$ gilt es wieder ein $p$-Gaugefunktional $\|\cdot \|_{\gamma _{1}}$ mit

$\|x\cdot y\|_{\beta _{1}}\leq M_{\gamma _{1}}\cdot \|x\|_{\gamma _{1}}\cdot \|y\|_{\gamma _{1}}$

für alle $x,y\in A$ und $M_{\gamma _{1}}\geq \max \left\{\|e\|_{\beta _{1}},\|e\|_{\gamma _{1}},M_{\beta _{1}}\right\}$.

Beweis 3 - Neutrales Element der Multiplikation

Ohne Einschränkung sei ferner $M_{\beta _{1}}\geq \underbrace {\|e_{A}\|_{\beta _{1}}} _{>0}$ gewählt werden und man erhält.

$\|x\|_{\alpha }\leq M_{\beta _{1}}\cdot \|x\|_{\beta _{1}}\cdot \underbrace {\|e_{A}\|_{\beta _{1}}} _{\leq M_{\beta _{1}}}\leq M_{\beta _{1}}^{2}\cdot \|x\|_{\beta _{1}}\cdot \|y\|_{\beta _{1}}$

Man definiert nun $\left\|\cdot \right\|_{(\alpha ,1)}:={M_{\beta _{1}}}^{2}\cdot {M_{\gamma _{1}}}^{2}\cdot \|\cdot \|_{\gamma _{1}}$.

Beweis 4 - Stetigkeit der Multiplikation

Ist nun $\left\|\cdot \right\|_{(\alpha ,k)}$ gegeben, so kann man wieder zu diesem $p$-Gaugefunktional $\left\|\cdot \right\|_{(\alpha ,k)}$ wieder $\|\cdot \|_{\gamma _{k}}$ finden, für das dann wiederum $\beta _{k},\gamma _{k}\in {\mathcal {A}}$ und $M_{\beta _{k}},\,M_{\gamma _{k}}>0$, die die folgende Ungleichung gilt:

• $\left\|x_{1}\cdot x_{2}\cdot x_{3}\cdot x_{4}\right\|_{(\alpha ,k)}\leq \displaystyle \prod _{i=1}^{4}\left(M_{\beta _{k}}\cdot M_{\gamma _{k}}\cdot \|x\|_{\gamma _{k}}\cdot \|x_{i}\|_{\gamma _{k}}\right)$
• Man definiert $\left\|\cdot \right\|_{(\alpha ,k+1)}:=M_{\beta _{k}}\cdot M_{\gamma _{k}}\cdot \|\cdot \|_{\gamma _{k}}$ mit $M_{\gamma _{k}}\geq \max \left\{\|e_{A}\|_{\beta _{k}},\|e_{A}\|_{\gamma _{k}},M_{\beta _{k}}\right\}$.

Beweis 5 - Abschätzung von Produkten mit 4 Faktoren

Produkte mit 4 Faktoren als Ungleichung abschätzen:

${\begin{array}{rcl}\displaystyle \left\|\prod _{i=1}^{4}x_{i}\right\|_{(\alpha ,k)}&\leq &\displaystyle M_{\beta _{k}}\cdot \|x_{1}\cdot x_{2}\|_{\beta _{k}}\cdot \|x_{3}\cdot x_{4}\|_{\beta _{k}}\\&\leq &\displaystyle M_{\beta _{k}}\cdot {M_{\gamma _{k}}}^{2}\cdot \prod _{k=1}^{4}\|x_{k}\|_{\gamma _{k}}\\&\leq &\displaystyle {\underbrace {M_{\beta _{k}}} _{\geq 1}}^{8}\cdot {\underbrace {M_{\gamma _{k}}} _{\geq 1}}^{8}\cdot \prod _{k=1}^{4}\|x_{k}\|_{\gamma _{k}}\\&\leq &\displaystyle \prod _{k=1}^{4}\|x_{k}\|_{(\alpha ,k+1)}\\\end{array}}$

Beweis 6 - Produkten mit 3 Faktoren

Mit der obigen Konstruktion kann man die Ungleichung auch auf Produkte auch für 2 oder 3 Summanden anwenden, indem man einzelne Vektoren als Einselement $e_{A}\in A$ der Multiplkation definiert werden. Im weiteren Verlauf wird die Abschätzung des Cauchy-Produktes auf der Polynomalgebra $A[t]$ benötigt man die obige Aussage lediglich für 3 Faktoren für das Kaskadenlemma. Daher setzt man in folgenden Ungleichung $x_{4}=e_{A}$.

Beweis 7 - Abschätzung von Produkten mit 3 Faktoren

Ungleichung mit 4 Faktoren auf $\|x_{1}\cdot x_{2}\cdot x_{3}\cdot e_{A}\|_{(\alpha ,k)}$ anwenden.

${\begin{array}{rcl}\displaystyle \left\|\prod _{i=1}^{3}x_{i}\right\|_{(\alpha ,k)}&\leq &\displaystyle M_{\beta _{k}}\cdot \|x_{1}\cdot x_{2}\|_{\beta _{k}}\cdot \|x_{3}\cdot e_{A}\|_{\beta _{k}}\\&\leq &\displaystyle M_{\beta _{k}}\cdot {M_{\gamma _{k}}}^{2}\cdot \underbrace {\|e_{A}\|_{\gamma _{k}}} _{\leq M_{\beta _{k}}}\cdot \prod _{k=1}^{3}\|x_{k}\|_{\gamma _{k}}\\&\leq &\displaystyle {\underbrace {M_{\beta _{k}}} _{\geq 1}}^{2}\cdot {\underbrace {M_{\gamma _{k}}} _{\geq 1}}^{2}\cdot \prod _{k=1}^{4}\|x_{k}\|_{\gamma _{k}}\\&\leq &\displaystyle {M_{\beta _{k}}}^{6}\cdot {M_{\gamma _{k}}}^{6}\cdot \prod _{k=1}^{3}\|x_{k}\|_{\gamma _{k}}=\displaystyle \prod _{k=1}^{3}\|x_{k}\|_{(\alpha ,k+1)}\\\end{array}}$

Beweis 8 - (K1) - Isotonie der Stetigkeitssequenz

Die Stetigkeitssequenz von Gaugefunktionalen ist isoton (d.h. $\|\cdot \|_{(\alpha ,k)}\leq \|\cdot \|_{(\alpha ,k+1)}$), denn für alle $x\in A$ gilt:

${\begin{array}{rcl}\|x\|_{(\alpha ,k)}&\leq &M_{\beta _{k}}\cdot \|x\|_{\beta _{k}}\cdot \|e_{A}\|_{\beta _{k}}\\&\leq &M_{\beta _{k}}\cdot {M_{\gamma _{k}}}\cdot \|x\|_{\gamma _{k}}\cdot \underbrace {\|e_{A}\|_{\gamma _{k}}} _{\leq M_{\gamma _{k}}}\cdot \underbrace {\|e_{A}\|_{\beta _{k}}} _{\leq M_{\beta _{k}}}\\&\leq &\underbrace {{M_{\beta _{k}}}^{2}\cdot {M_{\gamma _{k}}}^{2}\cdot \|x\|_{\gamma _{k}}} _{=\|x\|_{(\alpha ,k+1)}}=\|x\|_{(\alpha ,k+1)}\end{array}}$

Beweis 9 - (K2) - Kaskadenungleichung

Die Stetigkeitssequenz von Gaugefunktionalen wird schrittweise für 3 Faktoren angewendet:

${\begin{array}{rcl}\displaystyle \left\|\prod _{k=1}^{n}x_{k}\cdot y_{k}\right\|_{\alpha }&\leq &\displaystyle \left\|x_{k}\right\|_{(\alpha ,1)}\cdot \left\|y_{k}\right\|_{(\alpha ,1)}\cdot \left\|\prod _{k=2}^{n}x_{k}\cdot y_{k}\right\|_{(\alpha ,1)}\\&\leq &\displaystyle \prod _{k=1}^{2}\left(\left\|x_{k}\right\|_{(\alpha ,2)}\cdot \left\|y_{k}\right\|_{(\alpha ,2)}\right)\cdot \left\|\prod _{k=3}^{n}x_{k}\cdot y_{k}\right\|_{(\alpha ,2)}\\&\leq &\displaystyle \prod _{k=1}^{n}\left(\left\|x_{k}\right\|_{(\alpha ,k)}\cdot \left\|y_{k}\right\|_{(\alpha ,k)}\right)\end{array}}$

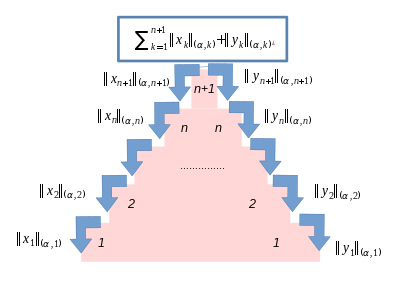
Kaskadenungleichung für Summen und Produkte

Verbinden Sie die Kaskadenungleichung für Prodkukte mit der Kaskadenungleichung für Summen.

Korrolar - Kaskadensequenz

Sei $(A,\|\cdot \|_{\mathcal {A}})$ eine unital positive topologische Algebra mit dem basiserzeugenden $p$-Gaugefunktionalsystem $\|\cdot \|_{\mathcal {A}}$, dann gibt es für alle $\alpha \in {\mathcal {A}}$ eine Stetigkeitssequenz ${\textstyle \left(\left\|\cdot \right\|_{(\alpha ,m)}\right)_{m\in \mathbb {N} _{0}}}$, die folgende Eigenschaften besitzt:

• (K1) ${\textstyle \left\|\cdot \right\|_{(\alpha ,k)}\leq \left\|\cdot \right\|_{(\alpha ,k+1)}}$ für $k\in \{1,\ldots ,n-1\}$
• (K2) ${\textstyle \displaystyle \left\|\sum _{k=1}^{n}x_{k}\cdot y_{k}\right\|_{(\alpha ,m)}\leq \sum _{k=1}^{n}\left(\left\|x_{k}\right\|_{(\alpha ,m+k)}+\left\|y_{k}\right\|_{(\alpha ,m+k)}\right)}$
• (K3) ${\textstyle \displaystyle \left\|\prod _{k=1}^{n}x_{k}\cdot y_{k}\right\|_{(\alpha ,m)}\leq \prod _{k=1}^{n}\left(\left\|x_{k}\right\|_{(\alpha ,m+k)}\cdot \left\|y_{k}\right\|_{(\alpha ,m+k)}\right)}$

Beweisaufgabe für Studierende

Beweisen Sie die obige Abschätzung im Korrolar, indem Sie die induktive Definition im Lemma über Kaskadenprodukte mit dem Lemma über Kaskadensummen verbinden und die induktive Definition für beide Kaskadenungleichungen vornehmen.

Siehe auch

• Lemma - Kaskadensummen

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Topologische%20Invertierbarkeitskriterien/Lemma%20-%20Kaskadenprodukte%20
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.